Rep:Mod2:Ptelefolone
Sergei Palmer Year 3 Computational Labs - Module 2: Bonding (Ab initio and density functional molecular orbital
The focus of this module to investigate the structures and bonding of various molecules though quantum chemical modelling techniques.
Analysing BH3
Optimisation
Trigonal planar, D3h BH3 molecule was created in Gaussview and all 3 B-H bonds set to 1.5Å. A very rough, but quick optimisation was performed [DFT: B3LYP (3-21G)] in Gaussian (output summary in fig. 1, Log file). Only a simple basis set was required for this calculation as BH3 is symmetrical and very simple. The optimised structure of BH3 () was found to have H-B-H bond angles of 120° and B-H bond lengths of 1.19Å. This is in close agreement with literature.[1]

Fig. 1 confirms the D3h point group as expected; its symmetrical nature is further illustrated by a dipole moment of 0.0 Debye. The near-zero RMS gradient confirms that the structure has been optimised to a global minimum (or potentially a local minimum/transition state). To further confirm that the optimisation completed successfully, the log output file can be opened in WordPad giving the following output:
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
All four were determined to have converged indicating a successful completion. Furthermore, the optimisation plots (fig. 2) show that the energy was minimised over four steps.

The graph of RMS Gradient Norm against optimisation step number shows that the fourth step produced a low enough gradient (i.e. 1st derivative equal to 0) that could be equated to being a minimum. Additionally, as the bond data was in agreement with literature, further optimisation was not necessary.
Vibrational Analysis

As alluded to earlier, despite the minimisation of the molecule such that the 1st derivative of its energy has been minimised to a near-zero value, this could actually be the result of a local minimum or transition state (maximum) where the slope of the energy function is also 0. To determine whether it is the global minimum which has been found, the 2nd derivative of this function can be taken; if positive, we have a minimum and if one is negative, we have a transition state (maximum). If more than one value is negative, the optimisation process has failed as a critical point has not be determined. Doing frequency analysis is akin to taking the 2nd derivative of the potential energy surface and this allows us to examine more closely the molecule in consideration. As well as this, it provides very useful information about the IR and Raman modes which can be compared with experimental data.
Here six vibrational modes are detailed, though from the spectrum (fig. 4), only three are actually visible. As can be seen from the table, there are two pairs of degenerate E' stretching modes at 1203.6 and 2737.4 cm-1. The A1' stretch is totally symmetrical and thus generates no dipole moment. Hence it is not visible on the spectrum as confirmed by its intensity of 0.0. As can be seen, the deviation from literature calculated values using more advanced ab initio techniques was very minimal confirming that only a simple basis set is required for small molecules such as BH3. The frequency analysis of BH3 was done using DFT: B3LYP (3-21G) - Log file. Summary shown in fig. 3.
| Table of peaks | Spectrum | ||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
Molecular Orbital Analysis

A full NBO analysis was also carried out using Gaussian (DFT: B3LYP (3-21G) - Log file, summary fig. 5) to compare with predicted molecular orbital shapes for BH3.
A diagram was drawn using molecular orbital theory. Without calculation, it is difficult to accurately predict the exact energy levels following the combination of the fragment orbitals. The predicted MO diagram was compared with the MOs calculated to see how accurately the theory predicted for this molecule.
| MO energies | MO diagram | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|

|
The lowest energy MO at -6.7302 kcal/mol corresponds to the a1' of boron and confirms that it is too low to take part in bonding and is responsible for the 1a1' on its own. MOs 3 & 4 are the degenerate pair which form 1e'. Next it is possible to see the non-bonding 1a2" followed by the second degenerate pair at 0.1888 which form 2e'. This confirms as predicted on the MO diagram that 2e' is lower in energy than 3a1'. This ordering is the hardest to predict qualitatively as a1' energy levels are below those of e' but s-p interactions are weaker than s-s. However this calculation has shown to be concordant with what was predicted.
Charge and NBO analysis of BH3

The Lewis deficient boron atom is bright green which indicating that it is highly positively charged as expected . The amount of positive charge on the boron is roughly equal to three times the amount of negative charge on one of the hydrogen atoms; thus the total molecular charge is 0 as the three hydrogen atoms cancel out the central boron.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33161 1.99903 2.66935 0.00000 4.66839
H 2 -0.11054 0.00000 1.11021 0.00032 1.11054
H 3 -0.11054 0.00000 1.11021 0.00032 1.11054
H 4 -0.11054 0.00000 1.11021 0.00032 1.11054
=======================================================================
* Total * 0.00000 1.99903 6.00000 0.00097 8.00000
This summary from the output file confirms this above analysis. Additionally, it is possible to look at the Natural Bond Orbital (NBO) analysis to investigate the s & p contributions to the B-H bonds. The electron density is partitioned out into atomic like orbitals which are used to form 2e-2c bonds.
NATURAL BOND ORBITAL ANALYSIS:
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99853) BD ( 1) B 1 - H 2
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 2 s(100.00%)
1.0000 0.0000
2. (1.99853) BD ( 1) B 1 - H 3
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 3 s(100.00%)
1.0000 0.0000
3. (1.99853) BD ( 1) B 1 - H 4
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 4 s(100.00%)
1.0000 0.0000
4. (1.99903) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
The first bond (BD) between boron (atom 1) and hydrogen (atom 2) shows a 44.48% contribution from B, which has a hybridisation of 33.33% s and 66.67% p and 55.52% from H which is 100% s character. Looking at the other three bonds, the same characteristics are shown and hence 3 sp2 hybrid orbitals have been formed by boron which interact with the sAOs on the hydrogen atoms. Orbital 4 is the core boron 1s orbital which is not involved in bonding (as previously demonstrated in the MO diagram) and no. 5 is the boron out-of-plane lone pair (LP*) which is starred to indicate that it is not occupied.
Optimising a molecule of TlBr3
The aim of this computation was to introduce the use of pseudo-potentials - these are vital when investigating inorganic molecules, which can be importantly applied to catalytic systems or main group metal containing compounds. Pseudo-potentials needs to be introduced as main group metal containing compounds will of course include a lot of electrons which results in relativistic effects that the basic Schrodinger equation cannot factor in. As most chemistry is based on the domination of valence electrons in bonding interactions, pseudo-potentials (or an effective core potential - ECP) can safely model the core electrons of an atom making the calculation easier. However, when dealing with these more complex systems, it is also necessary to improve the basis set used. This increases the number of functions which are used to describe electronic structure which produces a more complete picture of the system in consideration. For example it is possible to take into account the diffuse nature of the bigger d orbitals or the polarisation of electron density clouds, both essential when an accurate description in required.
Optimisation
TlBr3 was constructed in Gaussview; before optimisation, the point group symmetry was restricted to D3h with a very tight tolerance (0.0001). This helps to reduce computation time by avoiding optimisation to a transition state. The structure was then optimised using DFT: B3LYP (LanL2DZ). LanL2DZ uses a medium level basis set (D95V) on first row atoms and Los Alamos ECP (pseudo potentials) on heavier elements. This is a fairly effective medium-level basis set and should be suitable for this molecule.
TlBr3 was successfully optimised and found to have a Tl-Br bond length of 2.65Å (lit: 2.512Å[2]) and Br-Tl-Br bond angle of 120°.

Output summary
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.082839D-11
Optimization completed.
-- Stationary point found.

The output shows that a minimum was indeed found with a low RMS gradient; the plots in fig. 8 show that three steps were required in order to find the minimum point. A frequency analysis was then done to confirm that the optimisation had indeed found the global minimum.
Frequency Analysis
| Table of peaks | Spectrum | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
Like with BH3, only three of the stretches are visible on the spectrum. Again, there is a totally symmetrical stretch at 165.3cm-1 which causes no dipole moment and so does not appear. There are again two pairs of doubly degenerate stretches which account for two of the peaks. The final one is just the A2" umbrella stretching. As can be seen, none of the frequencies came out as being negative which elucidates that the structure of TlBr3 was fully optimised correctly. Additionally the close agreement of the calculated bond lengths with literature values back this statement up.
What is a bond?
When investigating the optimisation of molecules, it was often seen that no actual bond seemed to be present between two atoms in a molecule. Traditionally a bond is seen as a physical link between two atoms as a matter of convention and convenience; however clearly this depiction is very simplified and does not tell the full story of atomic bonding. Gaussview itself is programmed to utilise a bond between atoms when they are a certain distance apart, a number which is often pre-programmed into the software. However when it comes to inorganic molecules, the boundaries of where a bond starts or finishes is a little more hazy. Instead it is necessary to look at a bond as a region where two or more atoms share electron density between their valence orbitals. This sharing of electrons results in sufficient attraction between the two or more atoms to be considered a bond i.e. the electromagnetic attractive forces between the nuclei and the electrons is generally responsible for bonding.
Cis/trans isomerism in Mo(CO)4(L)2
In this section, two stereoisomers of Mo(CO)4(L)2 are investigated where L = PCl3. Initially the thermal stability of the two compounds will be calculated and compared, followed by the spectral characteristics. In the cis-isomer, four carbonyl absorption bands would be expected versus one for the trans-isomer. [3]
Conformer optimisation
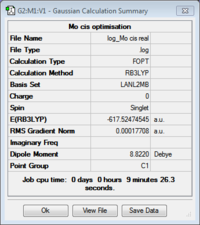
First of all, the ground state structures of cis and trans Mo(CO)4(PCl3)2 were optimised using the DFT: B3LYP method starting with a low level basis set and pseudo-potential (LANL2MB) to just rationalise the rough geometry. A loose convergence criteria was set to avoid the calculation taking too long.
| Cis summary Log file DOI:10042/to-10537 | Trans summary Log file DOI:10042/to-10538 |
|---|---|
 |
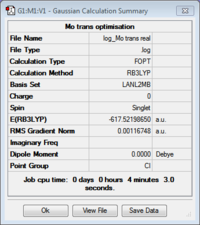 |
Taking the difference between the two isomers, it is possible to see that the cis form is slightly more stable the trans by 0.00275 a.u. (7.24 kJ/mol).
From these initially minimised structures, the torsion angles of the PCl3 groups were modified so that the starting point has the right orientation to find the lowest energy minimum. If the wrong starting point is chosen, a local minimum may be found which isn't quite as low in energy as the overall global minimum. In the cis case, one Cl group was rotated so that it pointed up, parallel to the axial CO group and that one Cl from the other group pointed down. For the trans conformer, both PCl3 were eclipsed so that one Cl of each group lay parallel to one Mo-C bond.
From these new geometries, optimisation was again done still with the B3LYP method, but this time with the LANL2DZ pseudo-potential and basis sets. The loose optimisation criteria was removed and replaced with "int=ultrafine scf=conver=9" in order to increase the electronic convergence. DZ (double zeta) is a much better basis set and pseudo-potential than MB (minimal basis) and hence should give more accurate results.
| Cis summary Log file DOI:10042/to-10764 | Trans summary Log file DOI:10042/to-10763 |
|---|---|
 |
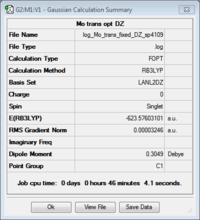 |
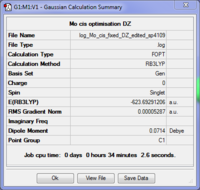
Again the cis is shown to be more stable than the trans conformer by 0.00104 a.u. (2.79 kJ/mol). Clearly the two basis sets agree with each other in this respect although LANL2DZ predicted a smaller difference in their energies. However according to the literature, the cis conformer isomerises to the trans form at room temperature[4] which would suggest that the trans isomer should be the more stable thermodynamic product compared with the more quickly formed cis, kinetic form. The LANL2DZ basis set doesn't take the phosphorus hypervalency and use of low lying dAOs into account; hence the dAO functions were manually added to the end of a new input file which was resubmitted for optimisation.
(blank line) P 0 D 1 1.0 0.55 0.100D+01 **** (blank line)
| Cis summary Log file DOI:10042/to-10820 | Trans summary Log file DOI:10042/to-10821 |
|---|---|
 |
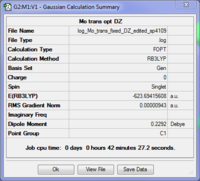 |
These summaries show that the trans conformer is now the more stable form by 0.00124 a.u. (3.27 kJ/mol) in agreement with the literature.
| Bond | Cis isomer | Cis isomer lit values[4],[5] | Trans isomer | Trans isomer lit values[4],[5] |
|---|---|---|---|---|
| Mo-P | 2.48 | 2.53 | 2.42 | 2.50 |
| Mo-C (axial) | 2.05 | 2.02 | 2.06 | N/A |
| Mo-C (equatorial) | 2.02 | 1.98 | 2.06 | 2.01 |
| C=O | 1.17 | 1.14 | 1.17 | 1.16 |
| P-Cl | 2.12 | 2.04 | 2.12 | 2.04 |
Vibrational Analysis
| Table of peaks | Spectrum | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
The four expected carbonyl peaks have been easily determined. However, in the output file, there were some negative frequencies which are detailed in table 9.
| Calculated Frequency (cm-1) | Vibration animation |
|---|---|
| -76.1 | 1 |
| -76.0 | 2 |
| -41.8 | 3 |
| -25.5 | 4 |
| -16.4 | 5 |
These negative frequencies are all resulting from the PCl3 groups stretching which suggests that at room temperature, the two isomers easily interconvert as a result of the minimal energy difference between the two. The basis set used therefore finds it difficult to differentiate between the two, resulting in these readings.
| Table of peaks | Spectrum | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
Although one carbonyl peak was expected, on the spectrum, these two calculated values are very close and are combined into the same peak. Again there were some negative frequency values in the output file.
| Calculated Frequency (cm-1) | Vibration animation |
|---|---|
| -82.0 | 1 |
| -63.7 | 2 |
| -55.9 | 3 |
| -48.3 | 4 |
Overall the expected peaks were observed in the spectra, though they were not all that concordant with the literature values found. Of course a computational method will find it difficult to be 100% accurate, but as only medium level basis sets were used, it was a pretty successful experiment.
Mini project
Introduction
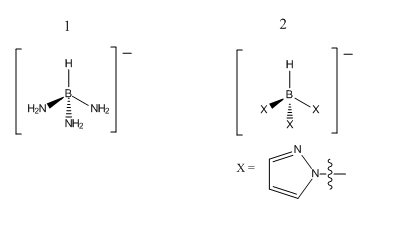
The aim of this miniproject was to investigate and compare the two molecules shown in fig. 9.
Optimisation
Using ab initio DFT methods, the geometries were optimised using initially the 6-31G (d,p) basis set with the method B3LYP. Following this, they were optimised slightly more with 6-311G (d,p). No pseudo potentials were required for this molecule as it contains no heavy atoms. After this, frequency analysis was done to confirm full minimisation of their energies as well as to produce IR spectra for comparison. Additionally the molecular orbitals of 1 were investigated using this method.
| 6-31G (d,p) summary DOI:10042/to-10813 | 6-311G (d,p) summary DOI:10042/to-10815 | 6-311G (d,p) optimised structure |
|---|---|---|
 |
 |
For molecule 1, using basis set 6-311G (d,p) produced a structure which was lower in energy by 0.0654 a.u. (171.6 kJ/mol) compared with when 6-31G (d,p) was used. This shows that the better basis set is able to determine a significantly lower energy conformation when dealing with these relatively simple molecules. The determined geometry of 1 showed that the 3 NH2 ligands were not all in the same orientation around the boron. Two of them had one hydrogen pointing down and one essentially equatorial whereas the other one had both hydrogens pointing upwards. All of the H-N-H bond angles are roughly 105° and the H-N-B angle is 107°. Hence these are all slightly distorted away from their ideal sp3 hybridisation. Optimised B-N bond length is 1.56Å (lit 1.42Å[7]). Optimised N-H bond length is 1.02Å (lit 0.983Å[7]). Optimised B-H bond length is 1.26Å (lit 1.19Å[7]). The optimised bond lengths are in good agreement with the literature values and so this clearly shows that 6-311G (d,p) is an effective tool for a molecule of this size.
| 6-31G (d,p) summary DOI:10042/to-10814 | 6-311G (d,p) summary DOI:10042/to-10817 | 6-311G (d,p) optimised structure |
|---|---|---|
 |
 |
For molecule 2, the output of 6-311G (d,p) optimisation gave a structure which was more stable than that produced by the 6-31G (d,p) basis set by 0.164 a.u. (430.6 kJ/mol). From both of these optimisations, it has been shown that 6-311G (d,p) is definitely a much more effective basis set in terms of finding the lowest energy of a molecule. Although it appears to take less time to optimise than the less complex basis set, this may just be as a result of the initial optimisation making the final job easier by bringing it close to the minimum. Like with the NH2 groups in molecule 1, two of the pyrazole ligands share the same orientation whereas the last one is inverted. The H-B-N bond angle for the two rings in the same orientation is 107° compared with 109° for the remaining one. All of the N-B-N bond angles are approximately 110°. Therefore despite having bulkier ligands, the bond angles in molecule 2 are less distorted from sp3 than with molecule 1. The B-N bond was found to remain the same as for molecule 1 (1.56Å); the B-H bond length decreased slightly to 1.20Å. This decrease may be as a result of the additionally electronegative nitrogen atoms in the pyrazole rings which cause the hydrogen to be drawn closer to boron.
When trying to perform these calculations to optimise 1 & 2, quite a lot of attempts were done in order to get it done correctly. Initially the 6-31G (d,p)/ 6-311G (d,p) basis sets were used; however all of these calculations failed (error link 9999) meaning that the molecule did not converge fully. After this, I tried to use the LANL2MB and LANL2DZ methods as I thought there may have been an issue with the large number of electrons. However these basis sets are not really applicable to the problem in question. Hence the original basis sets were used again, this time with the additional keywords "int=ultrafine scf=conver=9 OPT(MAXCYCLE)=50) which resulted in the successful optimisations as shown above. All of the DOIs below link to the original failed calculations or those performed with LANL2MB/DZ.
DOI:10042/to-10766 DOI:10042/to-10768 DOI:10042/to-10767 DOI:10042/to-10765 DOI:10042/to-10758 DOI:10042/to-10698 DOI:10042/to-10697 DOI:10042/to-10696 DOI:10042/to-10695 DOI:10042/to-10756 DOI:10042/to-10755 DOI:10042/to-10754 DOI:10042/to-10753 DOI:10042/to-10752 DOI:10042/to-10751
Molecular Orbital Analysis of Molecule 1
| Molecular Orbital | Image | Note |
|---|---|---|
| LUMO + 6 |  |
Less diffuse than LUMO+5. |
| LUMO + 5 |  |
Very diffuse electron density. |
| LUMO + 3 |  |
More antibonding character than bonding character. |
| LUMO + 2 |  |
Antibonding centered on two of the nitrogen atoms. |
| LUMO + 1 |  |
Fairly symmetrical in terms of bonding and antibonding components. May be non-bonding. |
| LUMO |  |
Very diffuse molecular orbital with a lot of nodes. Antibonding character centered on nitrogen atoms. |
| HOMO |  |
HOMO has quite a lot of nodes - may be higher in energy than expected. |
| HOMO - 1 |  |
Antibonding character coming from nitrogen (lone pairs possibly) |
| HOMO - 2 |  |
3 nodes but slightly more bonding than antibonding characteristics. |
| HOMO - 3 |  |
Antibonding character coming mainly from the hydrogen AOs. |
| HOMO - 4 |  |
4 nodes in this MO. Possibly high in energy and non-bonding. |
| HOMO - 9 |  |
3 nodes in this molecular orbital. May be a non-bonding MO. |
| HOMO - 12 |  |
If a molecular orbital diagram were to be drawn, this would be the first bonding MO as it is fully symmetrical. |
As you go further from the HOMO-LUMO region into the antibonding molecular orbitals (i.e. LUMO + 1/2/3...) the electron density becomes more diffuse. In fact by looking at the NBO analysis, it can be seen that the contribution of the dAOs to the bonding increases from 6.61% in the LUMO to 12.83% in the LUMO+3 to 35.13% for the LUMO+4 and 90.05% for the LUMO+5. Looking at table 14, this is clearly evident. Interesting, for the LUMO+6, the dAO contribution is down to 40% which is easily noted on observation.

Fig. 10 confirms as expected that the positive charge is centred on the lewis deficient boron atom similar to the case with BH3 discussed earlier. The highly electronegative nitrogen atoms are bright red as expected; unsurprisingly the hydrogen directly bonded to the boron is more negatively charged than the ones on the nitrogen atoms; this is because the electron density is drawn from them by the nitrogen resulting in a positively charged atom.
Frequency Analysis
| Table of peaks | Spectrum | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
| Table of peaks | Spectrum | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
Conclusion
Molecular orbital analysis of molecule 1 showed that the bonding between boron and nitrogen can be fairly complex as it is difficult to determine exactly what is happening. NBO analysis helped in that, by providing a breakdown of individual contributions from different orbitals, it was easier to rationalise the shape of the MOs.
In the frequency analysis, no negative values were obtained for either molecule. Hence this shows that the lowest possible state possible using these calculation methods had been successfully found. It was observed that the frequency at which the B-H bond stretch increased by 25% from molecule 1 to 2. The addition of extra electronegative heteroatoms into the molecular system could have been partly responsible for this.
Overall the DFT:B3LYP method with 6-311G (d,p) basis set proved to be a very effective tool in calculating the properties of these simple inorganic molecules. Had more time been available, it would have been useful to test it with a variety of different atoms at the centre instead of the boron. It would have been possible to really test the limits of this basis set to see where it would start to collapse before other sets like LANL2DZ which use pseudo-potentials would have been required.
References
- ↑ 1.0 1.1 Schuurman, M. S., Allen, W. D., Schaefer, H., F., J. Comp. Chem., 2005, 26, pp. 1106-1112
- ↑ Glaser, J., Johansson, G., Acta Chemica Scandinavica A, 1982, 36, 125
- ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/10a_MoC4L2_intro.html
- ↑ 4.0 4.1 4.2 Cotton, F. A., Darensbourg, D. J., Klein, S., Inorg. Chem., 1982, 21 pp. 294-299
- ↑ 5.0 5.1 Hogarth, G., Norman, T., Inorg. Chim. Acta., 1997, 254, pp. 167-171
- ↑ 6.0 6.1 Cotton, F. A., Inorg. Chem, 1964, 3, pp. 702-711
- ↑ 7.0 7.1 7.2 Briggs, T.S., Gwinn, W. D., Jolly, W.L., Thorne, L.R., J. Am. Chem. Soc., 1978, 100, 7762
- ↑ Ha, T.-K., Journal of Molecular Structure: THEOCHEM, 1986, 136, pp. 165-176
