Rep:Mod2:PorcupinePorridgeProject
Inorganic Project
Borazine is an interesting molecule. It is isoelectronic to benzene, and has the same planar geometry. However, when comparing atomic Boron, Carbon and Nitrogen, we see very different bonding and properties. The aim of this small project is to compare the structure & energy, electron distribution, vibrational spectra and molecular orbitals, not only of the isoelectronic benzene and borazine, but also other 6-membered rings containing alternating Gp III and Gp V atoms. I intend to look at trends within the molecules, as we move down the groups.
Benzene
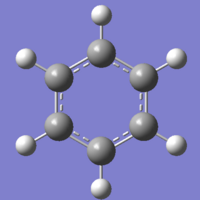
Benzene is a simple, aromatic 6-membered ring, consisting of 6 carbon atoms in a planar ring, with each carbon atom having a single hydrogen atom bonded to it, and the hydrogen atoms are also planar to the molecule. There are delocalised π clouds above and beneath the plane of the ring, causing great stability. The structure of benzene has been well documented due to it being the first documented aromatic molecule, and its unusual bond lengths, which are not as long as carbon-carbon single bonds, nor as short as carbon-carbon double bonds. The molecule here, was created by using the benzene fragment supplied in Gaussview, and was optimised initially using DFT/B3YLP and the 3-21G basis set. I chose the 3-21G basis set due to it's simplicity, and when dealing with low molecular weight atoms, in the constrained form of a small molecule, larger basis sets only lead to a few more decimal points of accuracy, whilst greatly increasing processor time.
| CC Bond Length (Å) | 1.40 |
| CH Bond Length (Å) | 1.08 |
| CCH Angle (o) | 120.00 |
| CCC Angle (o) | 120.00 |
The bond angles are exactly as expected - every atom is degenerate and so there should be no unbalanced forces causing distortions in the structure. The carbon-carbon bond length is close to the 1.39Å that is stated by all literature. The CH bond length is not as useful as expected, as the change in bond length from an sp hydrogen to an sp2 hydrogen is .01Å and the error of the calculations at this level, can easily causing rounding of the bond length to show either sp or sp2 character. The optimisation shows that without a doubt the molecule is planar, and this is due to the delocalised π systems above and beneath the plane, being much more stable when planar. Without the delocalised orbitals forcing planarity, we would expect to see the ring form a chair conformation, as in cyclohexane.
The previous output file was then used in a Gaussian job to find the vibrations within the molecule. None of the vibrations were negative, and so it seems that to the second order, the optimised state is the ground state. There are too many vibrations to look at, and so with the future molecules in mind, I chose to look at a select few. The top vibration is where we see the ring contract on itself slightly, with a large change in the position of the hydrogen atoms, as they move out from the centre of the ring. I chose it, due to it showing the strength of the bonding between the ring and the substituents. The second chosen vibration is where the 1,3 and 5 carbon atoms move towards the centre of the molecule, and then back out. The third vibration is where every respective CH group moves in towards the centre of the molecule, and in theory the vibration band is only due to C-C vibrations, and the hydrogen atoms are ignored.The last vibration band is due to the movement of the hydrogen atoms above and beneath the plane of the molecule. The main reason that these vibrations were chosen is that they are distinctive and should occur for each molecule, though for a molecule such as borazine, there might be 2 vibrational bands for a motion where benzene only has one.
| Diagram |  |
 |
 |
 |
| Freq (cm-1) | 3225.37 | 1064.43 | 1015.32 | 697.06 |
| Intensity | 0.00 | 0.01 | 0.00 | 117.61 |
| Charge | 0.00 |
| Spin | Singlet |
| Final Energy (Hartrees) | -230.9757 |
| RMS Gradient (Hartrees) | 0.0001 |
| Dipole Moment (D) | 0.00 |
| Point Group | C1 (D6h) |
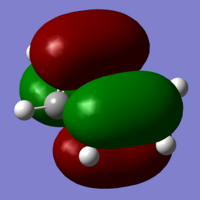 |
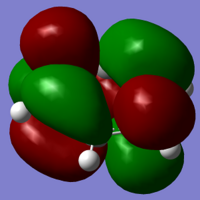 |
 |
The next stage of the computational molecular analysis are the molecular orbitals. Benzene has a very simple set of molecular orbitals, and to be able to compare structures and reactivity with the later molecules, it is again better to limit the data being compared. I've chosen to look at the HOMO and LUMO levels for the molecules, as these can give a good insight into the reactivity of a molecule, and its stability, on their own. The HOMO and LUMO for benzene are simple, as the ring is made of homo-atoms, and so we get C2 symmetrical orbitals.
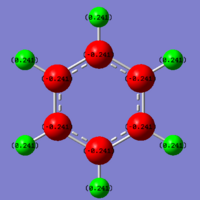
The final method for molecular comparison is the charge distribution within the molecule. This is easily achieved graphically by using the Gaussview interface to read the Gaussian output file, and viewing the NBO data, overlaid on the molecule. Within the benzene ring, the natural charge of each carbon atom, is paired with the opposite natural charge, from it's bonded hydrogen, reducing the effective charge of the molecule to zero.
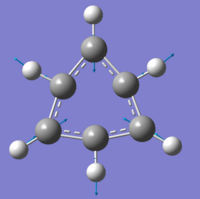
Borazine
| Charge | 0.00 |
| Spin | Singlet |
| Final Energy (Hartrees) | -241.3570 |
| RMS Gradient (Hartrees) | 0.0008 |
| Dipole Moment (D) | 0.0013 |
| Point Group | C1 (D3h) |

As mentioned earlier, borazine is isoelectronic to benzene, meaning that the total number of electrons within the molecule are the same. Boron has one less electron than carbon, whilst nitrogen has one more. Despite the structure, and the properties being discuss, all being controlled by electronic interactions, with the atomic size differing slightly, we still expect to see differences between the molecules, however. The method used for the creation of the molecule and the further optimisations, is identical to the one for benzene, to allow reliable the comparison of data.
When looking at the data to the right, it is slightly surprising to see the change in bond angles for the outside hydrogen atoms. The electronic properties i.e. electronegativity of the elements, are not directly proportional (linear), and so we would not expect to see identical bond lengths for the BN and CC bonds.
Although nitrogen is more electronegative than carbon, boron is much much less, and so we have a slightly longer ring bond in borazine. We can also see that the BH/NH bond lengths are above and beneath the CH bond length, respectively, again due to the electronegativity of the atoms - nitrogen, being more electronegative pulls the hydrogen atom closer to itself than the less electronegative boron, pulls its own hydrogen towards itself.
| BN Bond length (Å) | 1.45 |
| BH Bond length (Å) | 1.19 |
| NH Bond length (Å) | 1.02 |
| NBH Bond angle (o) | 121.51 |
| BNH Bond angle (o) | 118.49 |
| NBN Bond angle (o) | 116.99 |
| BNB Bond angle (o) | 123.01 |
The internal bond angles are closer to 120 degrees than I had expected, as the bond lengths are much more different when compared to benzene. I do not understand the reason why the external bond angles for the hydrogen atoms are not 120 degrees, as the molecule has a σh plane going through each NH/BH bond and so, there should be no preference to the angle at which the hydrogen atoms lie from the ring. Again, the molecule is planar, also due to the large delocalised orbitals preferring a planar conformation.
The vibrational table of borazine was found using the same method as the benzene.
The first vibration in the table relates to the stretching of all 3 NH bonds at the same time. Compared to the 3225.37cm-1 stretch we see in the benzene, we can see that the shorter, stronger bonds of NH compared to CH have a higher frequency of vibration, as you would expect. The next vibrational band is from the stretch of the three BH bonds at the same time. Due to the weaker, longer bonds of BH when compared to CH or NH, we get an expected decrease in the frequency of this vibration. The next two vibrations correspond to the second listed vibration of benzene. The atoms in the 1,3 and 5 positions (or 2,4 and 6) move in towards the centre of the molecule, and then back out. At the higher frequency, we have the 1, 3 and 5 atoms being boron atoms. The largest change in bond angle seems to be for the 1-2-3 type angle (i.e. the angle between three atoms, where the two terminal atoms are vibrating), and so with nitrogen orbitals being more 'rigid' and preferential of an sp2 conformation the vibrations occur at a higher frequency, than those mentioned next. The next band is at 855.93cm-1, and the atoms being moved are now the nitrogen atoms. The orbitals of the boron atoms are more distorted in these vibrations, and so we've lower frequencies of vibrations than when the nitrogen orbitals are more distorted. The final vibration is at 739.15cm-1 and is due to the movement of the hydrogen atoms above and below the plane of the ring. We see a bigger change in angle for the NH bonds, with respect to the plane of the ring, than for the BH bonds. This is because nitrogen is more stable than boron when forced into an sp3 conformation, especially as the bond angles are barely changed. When compared to the corresponding vibration for benzene, this vibration has a higher frequency, so the hetero- nature of the ring must make the whole system more electronically stable.
| Diagram |  |
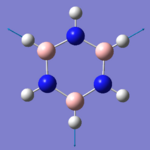 |
 |
 |
 |
| Freq (cm-1) | 3514.90 | 2681.69 | 947.76 | 855.93 | 739.15 |
| Intensity | 0.10 | 0.09 | 0.00 | 0.00 | 64.75 |
As with the benzene, we recorded the HOMO and LUMO of borazine, for comparison. The HOMO's have the same structure as each other, with a plane of symmetry separating the molecule into two halves, and each half has a different phase above and beneath the plane of the ring, and in both molecules, the phases change, when crossing the plane of symmetry. For example, a green lobe on one side of the molecule is represented by a red lobe on the other side. This is as you would expect, as the only real factor in the shape of molecular orbitals, is the electronics of the system, and the two molecules so far are isoelectronic.
 |
 |
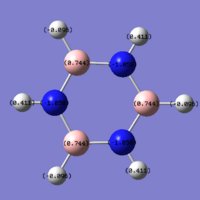 |
The charge distribution for borazine is more interesting than the benzene, but it is still easy to explain, just by comparing electronegativities. As mentioned many times before, the nitrogen atoms are more electronegative than either carbon or boron, and the natural charge is -1.058, as we would expect. As such, each hydrogen bonded to the nitrogen has a positive pseudo-charge, showing a natural charge of 0.411. The boron is much less electronegative than nitrogen, and in this case is electropositive, with a charge of 0.744, and the hydrogen atoms bonded to these boron atoms actually have negative natural charges of -0.096. Each BHNH groups has an overall natural charge of zero, and so the whole molecule has a charge of zero.
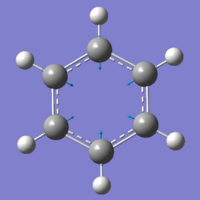
B3P3H6
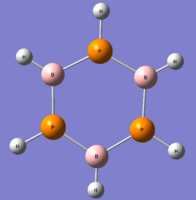
The next molecule being analysed is close to borazine, except the nitrogen atoms have been replaced by atoms of phosphorus -the element directly underneath it in Gp V.
| BP Bond length (Å) | 1.85 |
| BH Bond length (Å) | 1.18 |
| PH Bond length (Å) | 1.41 |
| PBH Bond angle (o) | 121.99 |
| BPH Bond angle (o) | 117.99 |
| PBP Bond angle (o) | 115.97 |
| BPB Bond angle (o) | 124.02 |
This molecule is not isoelectronic to either of the molecules looked at before, but there should be some similarities in structure and energy.
As expected, we see that the bond angles and lengths do relate to borazine, though there are some unexpected values. The B-P bond length here is much greater than that of the B-N length in borazine. This would be due to the much larger valence radius of the phosphorus, when compared to nitrogen and as such, the boron and phosphorus atoms cannot get as close to each other as the boron and nitrogen atoms, giving a much larger bond length. This increased radius must also be the reason for the increased PH bond length, which is larger than the CC bond length in benzene. The BH bond length for this molecule is very similar to that of the BH bond length in borazine, which surprised me - as I was expecting some electron distribution from the phosphorus atoms to decrease the bond length.
When a vibrational job was run of the molecule, again we obtained no negative frequencies, showing that we've been using the ground state for calculations.
The first listed vibration is the most similar to the first vibrations tabulated for the other molecules, but is not identical. All three hydrogen atoms on the boron atoms are moving from the centre of the ring, but not equally, and so this should be classed as an asymmetric stretch. The vibration here is of a higher frequency than the previous BH, leading me to conclude that the bonding BH has indeed changed on the substitution of nitrogen atoms for phosphorus.
| Diagram |  |
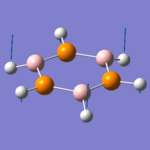 |
 |
 |
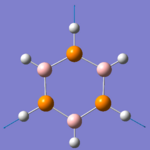 |
| Freq (cm-1) | 2746.94 | 756.61 | 658.79 | 495.15 | 433.11 |
| Intensity | 2.86 | 16.82 | 0.00 | 22.52 | 00.00 |
Another anomalous result for the vibrations, is that there is no single vibration band for the simultaneous vibration of the PH bonds - there are three separate ones instead, at 2443.26, 2445.00 and 2452.41cm-1. Each one of these vibrations has a lower frequency than the simultaneous vibration of the NH bonds in borazine. This could be due to the nature of the way the calculations predict the vibrations, making it impossible to compare single vibrations to simultaneous vibrations, although it is more likely to be different due to the massive change in size of the outer radius of phosphorus, when compared to nitrogen. The increased size of the atom makes the bond weaker and so the frequency of vibration should be much lower anyway. The next vibration band, at 756.61cm-1 is not just due to the NH hydrogen atoms vibrating above and beneath the plane, but also slight vibrations of the PH bonds. This vibration has a higher frequency than the simultaneous hydrogen shift band for the borazine at 739.15cm-1. It seems that as the ring atoms increase in size, the molecule as a whole becomes much more flexible, especially when compared to a similar molecule such as benzene.
The third vibration (658.79cm-1) in the list is due to the 1,3 and 5 atoms moving in towards the centre of the molecule and back out, and the atoms this time are the boron atoms. The frequency of this vibration is much lower than the same stretch for the borazine, and can again be explained by the relaxed bonding in the molecule, thanks to the increased size of the phosphorus. The next vibration is due to the 3 hydrogen atoms of the PH bonds vibrating above and beneath the plane. As such, this shows that the phosphorus atom in the ring can directly cause large geometrical changes, but also can have practically no effect on other aspects e.g. the BH bond length.
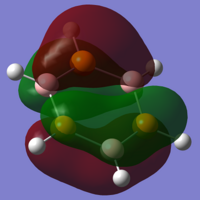 |
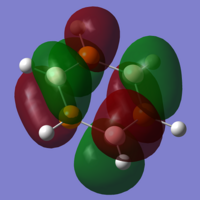 |
 |
The final vibration of note is the again due to the 1,3,5 vibration, but now the atoms moving are the phosphorus atoms. The frequency of this vibration band is almost 500cm-1 than the respective NH band in borazine, again due to the size of phosphorus.
As you would expect, the HOMO and LUMO for this molecule both have the same shape as the previous orbitals, though here it is clear to see that the calculations have not made the molecule symmetrical as there is visible distension of the lobes, especially in the HOMO, which is not clearly visible for the previous molecules.
The final stage of the analysis is to look at the charge distribution throughout the molecule. Using the NBO data used in the Gaussian calculations, we can see a lot of familiarities between this molecule and the borazine. The roles of the atoms within the ring have now changed, with boron now having a negative natural charge (-0.254), and the group 5 ring member now holding a positive natural charge (0.159). The magnitude of these natural charges are now much lower than those for the borazine, showing the strongly covalent nature of these bonds.
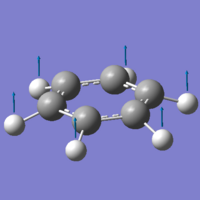
Al3P3H6
Up until now, the GpIII-GpV rings have all had planar ground states, and have shown that they've similar properties. In the progression of going down the groups, one of the possible molecules is Al3P3H6.
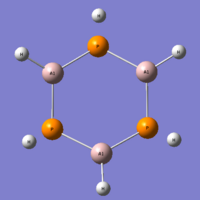
As you can see from the Jmol, this molecule is now in the chair conformation. If the molecule has its geometry minimized from the planar form, a stable output is found, however the vibrational analysis shows the molecule as having 3 vibrational bands beneath zero. Therefore, the ground state for this molecule can't be planar, and that the automatically assigned geometry is the ground state, as confirmed by the vibrational analysis. The structure for this molecule is very unusual, and just by eye, you would think that this conformation was unstable, or at least, not the ground state. It seems that the borons have tried to keep themselves in a planar sp2 form, and the aluminium atoms have rotated themselves as to create an sp3 atom. This combination of orbitals has led to all the hydrogen atoms pointing above the plane, and the aluminium lone pairs pointing beneath the plane. This could be a limitation of the basis set or method, but even if it cannot calculate the geometry exactly, it should still be a useful optimisation. I cannot find any literature for this molecule and may inquire with H. Rzepa, to further analyse the structure of this molecule.
| AlP Bond length (Å) | 2.33 |
| AlH Bond length (Å) | 1.60 |
| PH Bond length (Å) | 1.43 |
Looking at the bond angles for this molecule would not be of any use here, as they can only really be compared to other chair conformations of molecules (limited time, so route not explored). However, even just from the bond lengths, we can see that there has been a big change in the geometry of the molecule. The increased bond length within the ring is due to the very large radii of both types of ring atoms, and is much larger than any previous ring bond-lengths. The PH bond length has now barely changed, from the B3P3H6 geometry, despite the addition of the large aluminium atoms.
Being a wholey different geometry, comparing vibrational bands is not a priority, but there are still a few vibrational modes that exist in this molecule, that correspond to vibrations in the earlier molecules.
| Diagram | |
| Freq (cm-1) | 415.66 |
| Intensity | 75.73 |
The vibration on the left is the vibration most reminiscent of the earlier molecules, with the hydrogen atoms simultaneously moving towards, and away from a point, not a plane as this molecule is not planar. There are many interesting vibrations of this molecule, however due to time constraints, I cannot deliberate further - the raw data files are below.
The Gaussian software cannot calculate any molecular orbitals for this molecule, which could be due to the strange structure being unsupported by the calculations.
Conclusions The data from these calculations clearly show a trend of increasing bond lengths as you go down the group, as is obvious, but there also seems to be another underlying scheme, causing the geometry to change, not only by altering bond length, but by changing the conformation to an unusual structure.
If I had more time, I would have loved to repeat this project with more ring systems, and using a larger basis set. I would also have been able to spend more time on the analysis, as the project was pressed for time, due to problems with the Gaussian interface and long methods used to store the small pieces of data.
Collected Data
- Chk file for benzene molecular orbitals; https://www.ch.imperial.ac.uk/wiki/index.php/Image:Ross_benzene_mo.chk
- Log file for optimisation of benzene; https://www.ch.imperial.ac.uk/wiki/index.php/Image:ROSS_BENZENE_OPT.LOG
- Log file for vibrational analysis of benzene; https://www.ch.imperial.ac.uk/wiki/index.php/Image:ROSS_BENZENE_VIB.LOG
- Chk file for B3P3H6 molecular orbitals; https://www.ch.imperial.ac.uk/wiki/index.php/Image:Ross_B3P3H6_MO.chk
- Log file for optimisation of B3P3H6; https://www.ch.imperial.ac.uk/wiki/index.php/Image:ROSS_B3P3H6_OPT.LOG
- Log file for vibrational analysis of B3P3H6; https://www.ch.imperial.ac.uk/wiki/index.php/Image:ROSS_B3P3H6_VIB.LOG
- Log file for optimisation of Al3P3H6; https://www.ch.imperial.ac.uk/wiki/index.php/Image:ROSS_AL3P3H6_OPT_2.LOG
- Log file for the vibrational analysis of Al3P3H6; https://www.ch.imperial.ac.uk/wiki/index.php/Image:ROSS_AL3P3H6_VIB.LOG
- Log file for vibrational analysis of borazine; https://www.ch.imperial.ac.uk/wiki/index.php/Image:ROSS_BORAZINE_VIB.LOG
- Log file for optimisation of borazine; https://www.ch.imperial.ac.uk/wiki/index.php/Image:ROSS_BORAZINE_OPT_2.LOG
- Chk file for borazine molecular orbitals; https://www.ch.imperial.ac.uk/wiki/index.php/Image:Ross_borazine_homo.chk
