Rep:Mod2:CosGot

3rd Year Computational Chemistry Lab Report - Module 2
Student: Cosma Gottardi (Ceg08)

BH₃

Considerations about the structure and geometry of BH₃

The trigonal planar structure of BH₃, with specail attention being given to its bond lengths, was optimised using Gaussian via the Gaussview interface (log file), and the following parameters were found:

• optimised bond lenght: 1.19 Å
• optimised bond angle: 120.0 °

The type of calculation, including which basis set was used, along with the some important output parameters can be found in the table below.

Optimisation of the geometry of BH3
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.4623 Hartrees
RMS Gradient Norm	0.00020672 atomic units
Dipole Monment	0.0000 Debeye
Point Group	D3H
CPU time	22.0 s

The gradient of the potential energy curve used for minimisation being smaller than 0.001 we can conclude that the calculation has indeed converged and our findings are valid. The closer the gradient is to 0, the closer we are at a minimum: in physical terms, this gradient is like the sum of (the moduli of) the forces acting between the different atoms of the molecule into the position where the least repulsion between them takes place and the attractions are maximised. (When optimising to a transition state, the gradient will also be 0, however this latter "equilibrium" of forces will be an unstable one, i.e. a maximum in the potential energy curve. However this is not considered in this Module.)

Molecular Orbitals

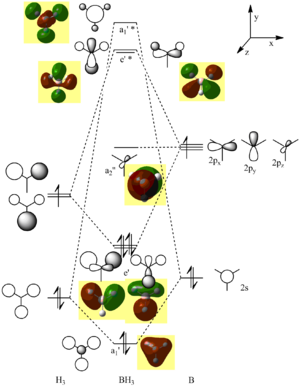
This is the logfile of the calculation in which the orbitals were calculated. By linearly combining the 1s orbitals of three Hydrogen atoms and the 2s and 2p orbitals of Boron, one can draw up an MO diagram by combining an H₃ fragment with a single B atom. The calculated MOs and the ones deduced using the simple, qualitative theory of constructive and destructive interference of orbitals of the same symmetry actually look very similar, with the only difference being that two neighbouring lobes of the same phase on neighbouring atoms in the LCAO merge into one big lobe in the Gaussian calculation. This highlights how important and powerful the simple qualitative method can be in obtaining first approximations to the actual MOs.

NBO (Natural Bond Order analysis)

One of the results of the NBO analysis done as part of the Energy analysis that also resulted in the calculation of the molecular orbitals above was that it showed the relative partial charges on each atom:

• -0.111 for each of the H's
• +0.332 for the B.

Vibrations

A Gaussian calculation was run to determine the infrared (vibrational) frequencies that Borane vibrates at. 6 vibrations were found (see also the log file) and they are reproduced in the table below.

No.	Form of the vibration	frequency	intensity	symmetry D3h point group
1		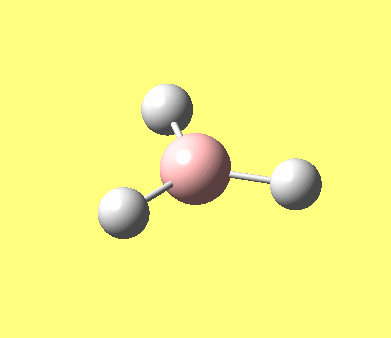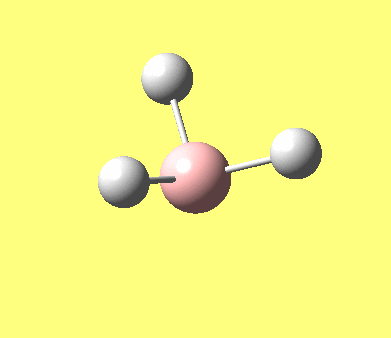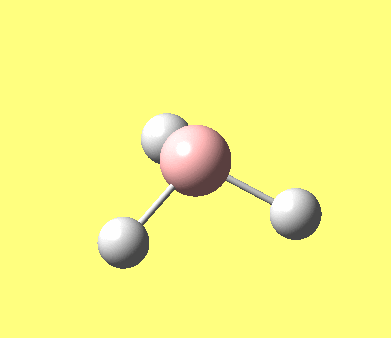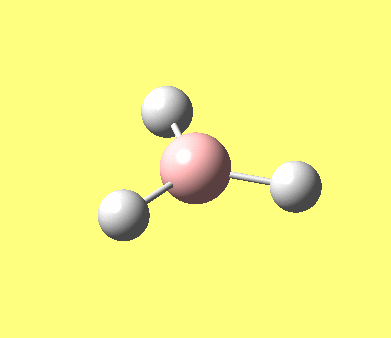1144.15	92.87	A"2
2		1203.64	12.31	E'
3		1206.64	12.32	E'
4		2598.42	0.00	A"1
5		2737.44	103.74	E'
6		2737.44	103.73	E'

Predicted IR-Spectrum of Borane

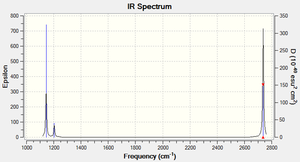
There are 6 different vibrations, however the Infrared spectrum only showes 3 peaks. There are two reasons for this: Firstly, each vibrational mode may or may not correspond to a change in dipole moment of the molecule. Since it is the electromagnetic radiation of the corresponding frequency that induces a change in the dipole moment and hece causes the vibration (resulting in a peak in the IR spectrum), a mode with no dipole moment will not be excited through IR radiation and hence show no peak in the IR spectrum, e.g. mode Number 4 above.

Secondly, if two vibrations are degenearate, they will resonate at the same frequency, thus giving rise to only one peak, which hovever in turn has a higher amplitude. This is the case for the modes 2 & 3 and 5 & 6.

TlBr₃

Optimising molecules with larger numbers of electrons - using pseudo potentials and larger basis sets

Using the LANL2DZ basis set the structure of TlBr₃ was optimised. To make the calculation faster the symmetry was fixed to be very close D_3h, as it is known from theory that this molecule is trigonal planar. The following info was found in the log file:

• optimised bond lenght: 2.65 Â (which compares reasonably well to a Tl-Br bond lenght of 2.481(2) Å measured for a TlBr₂⁺ ion)
• optimised bond angle: 120.0 ° (as would have been expected when setting the symmetry)

The following table contains a summary of the calculation output.

Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-91.2181
RMS Gradient Norm	0.00000090 a.u.
Dipole Monment	0.0000 Debeye
Point Group	D3H
CPU time	26.0 s

As with all calculations, a frequency analysis had to be carried out, to verify if this calculation was valid in the first place: In the log file of the vibrational analysis the so-called "low frequencies" (vibrational modes that would be exactly zero if our calculations were very accurate) have to be as close to 0 cm^-1 as possible, and the lowest actual vibrational frequencies need to be all positive. In our example the "low frequencies" are -3.4213, -0.0026, -0.0004, 0.0015, 3.9367 and 3.9367 cm^-1 respectively, and the lowest of the real vibrational modes is at 46 cm^-1. Had the frequency analysis not met all the conditions above, it would have been a strong indication that something during the optimisation had gone wrong, e.g. the energy minimum might not have been a global minimum, or a more accurate way (e.g. bigger basis set) of calculation would be necessary.

Thoughts about what a bond is

Chemists like to think of molecules in terms of bonds that join two atoms together. The line we draw between two atoms is representative of a pair of electrons that are shared between the two. This representation appears very early in the history of chemistry and is especially useful for considering Lewis structures. It is still the most important feature in the drawing of most molecules, especially in organic chemistry. In molecules that are more elaborate than just a simple diatomic, however, the molecular orbitals that are formed can be much more versatile and complex than simple σ and π bonds. What we call bond in a molecule sometimes is nothing more than a short distance between two atoms, often with a certain density of electrons between the two. Gaussian, which uses pre-defined atom to atom distances to decide whether a bond is to be drawn, hence will not always respect where Chemists (thinking of lewis structures) would like to see bonds drawn.

Cis-Trans isomerism in a Molybdenum Tetracarbonyl complex

These were the molecules under study:

• cis-tetracarbonyl-bistriphenylphosphine-molybdenum
• trans-tetracarbonyl-bistriphenylphosphine-molybdenum

The computationally demanding triphenylphosphino groups were replaced by trichlorophosphino groups which have similar electronic and steric properties

After having optimised the structures of the two compounds for their lowest energies, first using a low-level LANL2MB basis set (logfile for cis), manual alterations to find even lower energy conformers, finishing with LANL2DZ optimisations (logfiles for the cis and trans isomers) and finally also taking into account the Phosphorus's d-orbitals by using an extra basis (logfiles for the cis and trans isomers), the results were checked for un-reasonable or negative vibrations by performing a frequency analysis on both isomers (logfiles for cis and trans).

Structural considerations

Molybdenum to Phosphorous bond lengths as found after optimisation:

• in the cis compound: 2.48 Å
• in the trans compound: 2.42 Å
• experimentally in a similar complex: 2.4442(12) Å

This analysis shows that the bond-lenghts obtained through calculation are reasonable and that it is unlikely that our calculations contain human mistakes.

In comparing the two isomers in this property, we see that the cis geometry has a longer Mo-P bond length, which can probably be attributed to the steric interactions between the two trichlorophosphino groups forcing each other farther away from the metal centre.

Relative Energies of the two isomers

The energies found for the two isomers using the method described above were:

• -623.69291 (± 0.0038) Hartrees for the cis isomer and
• -623.69416 (± 0.0038) Hartrees for the trans isomer.

Hence, from a thermodynamic viewpoint, the trans isomer is more stable by 0.00124 Hartrees (± 0.0038) = 3.26 kJ/mol ± 10 kJ/mol. The errors quoted are those taken from the notes on accuracy page. The error being larger than the difference suggests that the difference is actually not significant! Maybe, however, one should/could revise the error limits given on that page, or rather perform a higher level calculation (which however on the downside would take more calculation time). Thermal energy at room temperature is about 2.48 kJ/mol. This makes it impossible for the trans geometry to convert into the cis, because at least another 0.8 kJ/mol (plus the energy of the kinetic barrier) would be required to cause that transformation. However, having no knowledge about the (energy of) this transition state between the two geometries, we cannot say whether the cis turns into the trans at room temperature (even though it would be thermodynamically favourable) or whether the cis can exist at room temperature without converting. This could be the starting point for further analysis: from it one could even determine the temperature of interconversion (supposing the molecules were stable and did inter-convert without decomposing). It could be of interest to see what one needs do to the triphenylphosphino ligands (modelled by the trichlorophosphino groups for ease of calculation in this exercise) to alter the relative energies of the two isomers. Since I assume that the main thing responsible for the difference in energy between the isomers is the steric repulsion of the two phosphino ligands in the cis complex which does not happen in the trans. By drastically reducing the size of the R groups on the phosphino ligand, e.g. by using Methyls (-CH₃) instead of the Phenyl rings (Ph = C₆H₅), these steric interactions could be minimised. To really force the molecule into having two phosphino ligands cis to each other one could consider joining the R groups of the two phosphino ligands together, effectively creating a bidentate ligand.

vibrational analysis and discussion of the IR spectrum

Low vibrational modes

Fortunately, the calculations did not output any negative vibrational frequencies. However on analysing the lowest frequency vibrations, we see some rotations of the phosphino ligands: at relatively low wavenumbers (between 5 and 20 cm^-1):

isomer	vibration No.	frequency of vibration / cm-1	animation	interpretation
cis	1	12		conrotation of the two phosphino ligands
cis	2	20		disrotation of the two phosphino ligands
trans	1	5		rotation of the two phosphino ligands in the same direction vs. the rest of the molecule
trans	2	7		rotation of the two phosphino ligands in opposite directions

A room temperature, k_BT = 2.478 kJ/mol = 207.2 cm^–1, which means that the thermal energy present (usually as translational kinetic energy) could well cause these vibrations to occur with a fairly high amplitude when translational to vibrational energy transfers occur, e.g. when two molecules "bump" into each other some of the translational motion might excite the molecules into their first and second excited vibrational state. The amplitude of the vibrations can be expected to be fairly high, so that eventually the chlorine atoms (or the phenyl groups) will be rotating around the phosphorous atoms.

The next vibrational states are at 46 and 40 cm^-1 for the cis and trans isomers respectively. One can expect it to be harder for the molecule to reach these states at room temperature without specific excitation (using IR light). These states and the next ten or so respectively are various bending modes of the molecules.

Carbonyl vibrations

complex	vibration No.	calculated frequency / cm-1	literature or experimental frequency / cm-1	description of vibration	point group and symmetry tag	Graphical representation
cis	42	1938	R=Cl: 1986 lit. R=Ph: 1840 (experimental)	antisymmetric C=O stretch of the two trans carbonyls	C2v: B1
cis	43	1941	R=Cl: 1994 lit, R=Ph: 1871 (experimental)	antisymmetric C=O stretch of the two cis carbonyls	C2v: B2
cis	44	1952	R=Cl: 2004 lit, R=Ph: 1895 (experimental)	symmetric stretch of the two trans carbonyls in antiphase with a symmetric carbonyl stretch of the two cis carbonyls	C2v: A1
cis	45	2019	R=Cl: 2072 lit, R=Ph: 2024 (experimental)	symmetric C=O stretch of all carbonyls	C2v: A1
trans	42	1939	R=Ph: 1891 (experimental), 1902 lit.	antisymmetric C=O stretch of 2 opposite carbonyls	D4h: Eu
trans	43	1940	R=Ph: 1891 (experimental), 1902 lit.	antisymmetric C=O stretch of the other two opposite carbonyls	D4h: Eu
trans	44	1967	(not observed)	symmetric CO stretch of opposite carbonyls, with adjacent carbonyls in antiphase (not IR active)	D4h: B1g
trans	45	2025	(not observed)	symmetric CO stretch of all carbonyls (not IR active)	D4h: A1g

Vibrations 42 and 43 of the trans complex should be degenerate, which they are (difficulties in calculation and the fact that the phosphino ligands are locked in one conformation give rise to the 1 cm^-1 difference.

Mini Project

The aim of the project was to analyse the dimeric species Al₂(CH₃)₆ in terms of bonding by looking at the and stability by comparison with the Al(CH₃)₃ monomer. The suitability of the Methyl group as a bridging ligand was also examined by comparison with the Chloro group.

	Energy 6-31G(d,p) / Hartree
AlMe3	-362.20384
Al2Me6	-724.42582
Al2Me6 - (2 * AlMe3)	-0.01814

The dimer is stabilised by 0.01814 Hartree = 48 kJ/mol compared to the monomer. The thermodynamically very favourable process of dimerisation readily occurs because the aluminium is not sterically hindered - in its trigonal planar geometry there are two open faces where it can readily react with other molecules.

Correlation table for some selected vibrations in the three dimeric molecules:

All vibrations given in wavenumbers, cm-1. (The numbers in parenthesis are the number of the vibrational mode in the output file of the respective compound)
	Al2Me6	Al2(μCl)2(Me)4 (Chloro bridging)	trans-Al2(μMe)2(Cl)2(Me)2 (Methyls bridging)
μ ligand rocking (with respect to each of the Al centres)	297 (16)	230 (15)	310 (15)
Al-Al stretch	312 (17)	213 (14)	305 (14)
μ ligand scissoring (with respect to each of the Al centres)	354 (18)	307 (16)	359 (16)
μ ligand-Al stretching (symmetric)	443 (19)	319 (17)	446 (17)
μ ligand-Al stretching (antisymmetric)	481 (20)	343 (18)	510 (20)
non-bridging ligand-Al stretch (antisymmetric)	558 (21)	569 (19)	Cl-Al: 456 (18) Me-Al: 645 (23)
non-bridging ligand-Al stretch (symmetric)	588 (23)	579 (20)	Cl-Al: 508 (19) Me-Al: 673 (24)
Energy, 6-31G(d,p)		-1565.1481 Hartree	-1565.1248 Hartree

Jmol Script for Al₂(CH₃)₆ to better illustrate the above vibrational modes.

Mini-Project

Looking at the relative energy difference between the two isomers with chloro ligands, we can see that Al₂(μCl)₂(Me)₄ is more stable by 0.0233 Hartree = 61 kJ/mol, which can mainly be attributed to the fact that the chlorine atoms are bridging. In comparing the vibrational frequencies of the three bridged compounds, we can see how similar the Methyl vibrations of Al₂Me₆ match with those of Al₂(μCl)₂(Me)₄ and Al₂(μMe)₂(Cl)₄(Me)₄, while the Cl-Al frequencies are lower, as we would expect, since Cl is a heavier atom, but unfortunately we cannot compare these quantitatively because the molecules are not diatomics where we could calculate the reduced mass and compare bond strengths. What is however interesting to note is that the Al-Al stretching frequency is a lot lower when the Chlorine atoms are bridging - this is because the bond is longer (3.35 Å instead of 2.60 Å).

NBO analysis:

charges of the atoms in the two chlorinated molecules

atom or group	charge when bridged	charge when not bridged	difference
Cl	-0.50	-0.54	-0.04
C	-1.43	-1.34	+0.09
H	0.30	0.26	-0.04
Methyl	-0.53	-0.57	-0.04

(the charge of the Aluminium centres is +1.66 and +1.63 for the chloro and methyl bridged compounds respectively.)

After a short calculation to find the total charge of the methyl groups, we see that the difference in charge from bridging to terminal ligand is about the same for both ligands - one could have expected that the more electronegative chlorine would be "stronger" in holding back its electrons from the Al centres.

Further analysis in this project could look at the NBO in more detail and discuss the hybridisation of the Al centres, and an MO analysis could explain further why the chloro ligands are more favourable as bridging ligands.

Logfiles for the dimeric species:
Al2Me6 Geometry optimisation; Al2Me6 Frequency analysis; Al2Me6 Energy (orbital analysis failed but NBO analysis worked)
Al2μCl2Me4 Geometry optimisation; Al2μCl2Me4 Frequency analysis; Al2μCl2Me4 Energy (orbital analysis failed but NBO analysis worked)
Al2μMe2Cl2Me2 Geometry optimisation; Al2μMe2Cl2Me2 Frequency analysis; Al2μMe2Cl2Me2 Energy (orbital analysis failed but NBO analysis worked)

Logfiles for the monomer:
AlMe3 optimisation log file; AlMe3 frequency analysis log file (there are some negative frequencies, since however the same method must be used to compare the monomer and dimer, this inaccuracy had to be tolerated, since a more precise and hence more computationally demanding method was not possible for the dimer.)