Rep:Mod2:240189cra

Section 1

Analysis of BH₃

Geometry Optimisation

Distortion of the BH₃ molecule, away from it's inital starting parameters (eg. all B-H bond lengths set to 1.5Å), followed by optimisation, using the DFT-B31YP method and 3-21G basis set yieled the following results.

BH₃ was successfully optimised to it's optimum conformation. Comparison to the experimentally observed bond length revealed this to be correct.

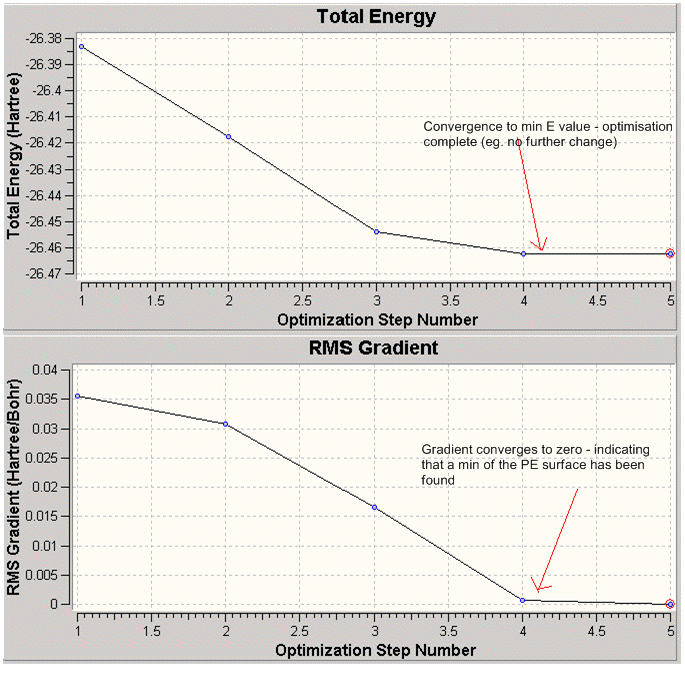
The plots of the total energy and the RMS gradient against the optimisation step indicate the successful completion of the optimisation.

What is a gradient?

• Take the PES of a BH₃ molecule
• The minimum on this surface represents the equilibrium conformation of BH₃ (eg. the lowest energy conformation)
• By taking the first derivative of the PES (N.B -dE/dr = Force, therefore at minima forces on molecule are balanced)the stationary points can be found. Hence, the optimised structure can be isolated.

How can maxima/ minima stationary points be distinguished?

• When dy/dx = 0, this is true for both maxima (transition states) and minima (ground state conformation)
• In order to distinguish between the two, the second derivative of the PES can be calculated
• This second derivative equates to the freqencies of vibration of the molecule
• Hence, if all vibrations are positive, a successful optimisation can be confirmed (see next section).

Fig.1. Optimisation of BH₃

Calculation Summary for Optimisation of BH₃

		Comment
File Type	log	Guassian output file
Calc. Type	FOPT
Calc. Method	RB3lYP
Basis set	3-21G
Energy/a.u.	-26.46
RMS grad. Norm. /a.u.	0.00000285	< 0.001 - suggests optimisation complete
Dipole mom. /Debye	0.00
Point Group	D3h	Correct- can be confirmed by inspection
Job CPU time	28 s

Table.2. Optimised parameters of BH₃ compared to lit.

	Calculated value	Lit. value
optimised B-H bond length/Å	1.19(435)	19.00
optimised H-B-H angle/°	120.0

From the graphs (Fig.1.), it can be seen that BH₃ was successfully optimised in 4 steps. The fifth yields the same result as the 4th, hence the optimisation was terminated.

Vibrational Analysis

Using the same method and basis set as before the vibrations of BH₃ were computed.

The output file was checked to ensure the calculation had successfully converged:

        Item               Value     Threshold  Converged?
Maximum Force            0.000090     0.000450     YES
RMS     Force            0.000064     0.000300     YES
Maximum Displacement     0.000354     0.001800     YES
RMS     Displacement     0.000250     0.001200     YES
Predicted change in Energy=-4.767110D-08
Optimization completed.
   -- Stationary point found.

The output file was also searched to find the values of the 'low frequencies'. As should be expected there are 6 of these (eg. from 3N-6) and can be confirmed to be much smaller than the observed vibrations. The output file also lists the vibrations along with the corresponding symmetry, energy and IR intensity. This information has been summarised in table.??.

Full mass-weighted force constant matrix:
Low frequencies ---   -0.3716   -0.0098   -0.0019   37.2426   37.9575   37.9593
Low frequencies --- 1146.0292 1204.8630 1204.8640
Diagonal vibrational polarizability:
       0.6047526       0.6046824       1.8987108

Of significance is the fact that all of the vibrations are positive, confirming, for reasons already noted, that the optimisation carried out in the above section was successful (eg. a minima was found).

Table.?. Vibrational analysis of BH₃

no	Description	Freq./cm-1	IR intensity	Symmetry (D3h point group)
1	'Umbrella' type motion; symmetric bend; B atom moves down, as H atoms bend upwards, to preserve the CoM	1146	92.7	A"
2	In plane bend - 2 H atoms bend towards eachother, reducing one H-B-H angle, whilst the other 2x H-B-H angles must expand	1205	12.4	E'
3	In plane bend	1205	12.4	E'
4	Symmetric stretch; simultaneous stretching of all three B-H bonds; B atom stationary;not IR active - no change in dipole moment	2592	0	A'
5	Asymmetric stretch: one H atoms stretches away from the B centre whilst the other comes towards it eg. out of phase stetching; 3rd H atom is stationary; B atom moves slightly from side to side to compensate for H motion	2730	103.9	E'
6	Asymmetric stetch: 1 x H atom stretches out whilst the other two, in phase, come towards the B centre; B atom shows slight displacment	2730	103.9	E'

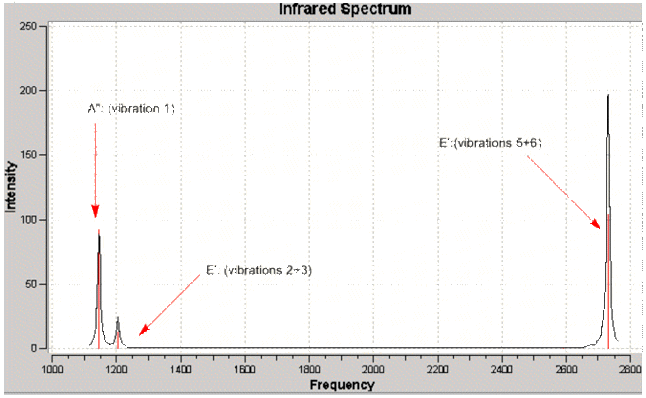
Although six separate vibrations are listed above, it can bee seen that there are two sets of degenerate vibrations. Based on this only 4 peaks would be expected. However, it is also evident that one of the vibrations does not result in a change in dipole moment, hence has zero IR intensity - resulting in 3 peaks as seen on the IR spectrum.

Fig.? Predicted IR spectrum of BH₃

MO analysis of BH₃

Fig.?. MO diagram of BH₃ showing the LCAOs and 'real' MOs. N.B the 1a'₁ MO/ 1s B AO should be much lower in energy

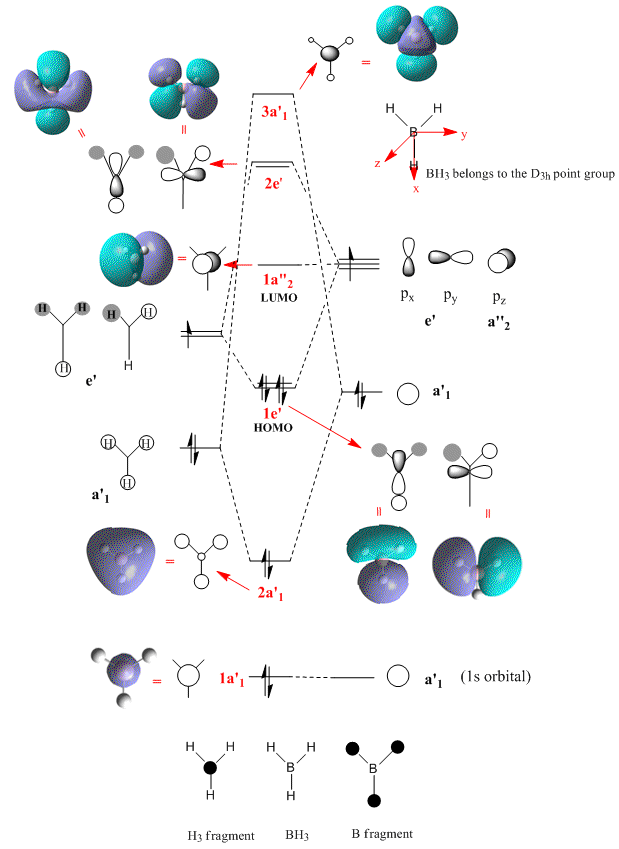
The molecular orbitals of BH₃, and their respective energies, were calculated using the DFT- B3LYP method and the 3-21G basis set.

How do the MOs generated via this quantitative, quantum mechanical approach, compare with the the respresentations of MOs generated from the LCAO qualitative approach?

Atomic orbitals (AOs) have been used as a basis set to form the MOs in the qualitative approach. As a result the MOs appear to be, very much centred on the atoms. Although the relative contributions of each AO to the MO can be represented to an extent(eg. the relative size), it is harder to visualise how the AOs interact/mix in 3D to give the final MO.

DFT (density functional theory), based on quantum mechanics, uses the electron density (eg. the probability of an electron being at a particular point in space), over all space, to solve the problem. As a result, the MOs generated show a greater degree of delocalisation over the whole molecule (eg. the HOMO-1, 2a'₁, MO).

When comparing the LCAO MOs with the calculated ones, it can be seen that LCAOs offers a very good first approximation. The relative ordering and degeneracy of the MOs is correct, the phase of the orbitals is correct and a rough idea of how the 3D MOs might look can also be gained (this is generally more difficult for the antibonding orbitals with out of phase interactions).

However, the LCAO approach has restricted itself to only using a limited number of atomic orbitals and does not take into account other possible effects that may impact on the MO . eg. electron - electron interactions. It is therefore not surprising that some of the calulated MOs take forms that could not be approximated using LCAOs ie. the shape of one of the 2e' MOs would be quite difficult to get completely correct.

As metioned, the relative ordering of the MOs shows good agreement. However, the ordering of the 3a'₁ and the 2e' orbitals is difficult to ascertain for sure. In the MO diagram shown, the 3a'₁ orbitalal has been drawn higher in energy than the 2e' orbital, due to the fact that this is the order that the quantitative approach resulted in. Nevertheless, a look at the energies of these orbitals shows that there is not a large degree of separation (eg. when compared to the HOMO and HOMO-1), and hence using a different quantitative method or basis set could alter this.

Using LCAOs to predict MOs before analysing the 'real' calculated ground state MOs would probably be a good place to start (for managable systems at least), allowing some degree of feeling for whether the calculated MOs look plausible.

Relative energies of the selected MOs

MO	Energy/au
1a'1 (HOMO-2)	-6.730
2a'1(HOMO-1)	-0.517
1e' (HOMO)	-0.356
1a"2 (LUMO)	-0.074
2e' (LUMO+1)	0.188
3a'1 (LUMO+2)	0.191

Analysis of BCl₃

Geometry Analysis

To optimise BCl₃, use of a pseudo potential [1],to simplify the model of the core electrons, is required.

Calculation Summary for Optimisation of BCl₃

		Comment
File Type	log	Guassian output file
Calc. Type	FOPT
Calc. Method	RB3lYP
Basis set
Energy/a.u.	-69.44
RMS grad. Norm. /a.u.	0.00005905	< 0.001 - suggests optimisation complete
Dipole mom. /Debye	0.00	Individual B(δ+)-Cl(δ-) dipoles cancel out
Point Group	D3h	Correct- can be confirmed by inspection
Job CPU time	12s

Optimised parameters of BCl₃ compared to lit.

	Calculated value	Lit. experimental value
optimised B-Cl bond length/Å	1.86(592)	1.742
optimised Cl-B-Cl angle/°	120.0	(planar)

The calculated bond length shows ~0.12Å difference from the experimental value. The calculated bond length can be quoted to 2dp, so the observed difference is greater than the error margin of the calulation. This indicates that the method/basis set used are not quite accurate enough. Using a higher level basis set (LanL2DZ), gives a value of 1.78(730)Å, much closer to the experimental value.

Fig.? Summary of LanL2DZ opt. of BCl₃

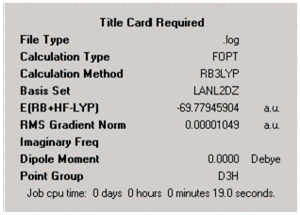
The ground state symmetry of BCl₃ can be predicted to be D_3h (Fig.)

Fig. Symmetry elements of BCl₃

The calculations for the optimisation and vibrational analysis only took 12 and 19 seconds respectively. This is short period of time, but it ought to be considered that BCl₃ is a realtively simple molecule, and that only a mdoerately sufficient basis set was used in the calculation. Hence, for more complicated jobs (see following sections), the SCAN service, with greater computing power, is required to run them.

Guassview and Bonding

Gaussview does not always draw in the expected bonds for a molecule. e.g. it might replace a triple bond with a double or single (see mini project) or even not draw in a bond at all (see cis - trans isomerisation). This does not mean, however, that the expected bond is not present. It does mean that the bond is outside the parameters/criteria Guassview sets for the expected bond. Hence, as Guassview uses data largely from organic chemistry to base it's bonding model on, any bond 'unusual' with respect to this, eg. inorganic complexes, may not be fully recognised (eg. it is not drawn in by Guassview but the atoms still does occupy the correct regions of space).

This leads to the question; what is a bond?

Consider a diatomic molecule. When the individual atoms approach one another, such that the interactions between them result in overall stabilisation (eg. a decrease in total energy w.r.t. the sum of the individual atomic energies), the atoms are considered to be bonded. How can this bond be described? Using a localised view, it could be described as a region of high electron density between the atoms, such that they now exist as a 'bound' entity.

Using MO theory,a more delocalised view of bonding, a bond could be described as existing if the electrons from the participating atoms occupy regions of constructive interference between the AOs rather than deconstructive eg. if the elctrons occupy MOs (regions of space) where they result in a lowering in energy of the molecule w.r.t the individual atoms.

Vibrational Analysis

The frequencies of vibrations for BCl₃ were computed, using the same method and basis set as the optimisation (see above).

Why is it important to use the same method and basis set for both the optimisation and frequency calculations?

• Vibrational analysis can be used to determine whether or not a structure has been successfully optimised (calculated frequencies are related to the second derivative of the PES of the molecule -see earlier discussion)
• The results will only be relevent, however, if the method/basis set are the same in both calculations.
• If a different method/basis set were to be used, the frequncies calculated may not relate to the optimised molecule in question, and hence, analysis of the success of the optimisation would not be possible.

The output file was consulted to ensure that the calculation had succssfully converged and that the 'low frequencies' were sufficiently smaller than the main vibrations (which they are):

Low frequencies ---   -8.7725   -4.0872   -4.0872   -0.0021    0.0050    0.0093
Low frequencies ---  214.1314  214.1321  376.9406

Axis system defined for BCl3

Table.?. Vibrational analysis of BCl₃

no	Description	Freq./cm-1	IR intensity	Symmetry (D3h point group)
1	'Wagging' type motion. All atoms are being displaced from their equilibrium position.	214	4	E'
2	In plane bend - 2 Cl atoms bend towards eachother, whilst the remaining BH unit is displaced along the x axis	214	4	E'
3	B centre moves up and down the z axis. H atoms remain stationary.	377	44	A2"
4	Symmetric stretch; simultaneous stretching of all three B-Cl bonds; B atom stationary;not IR active - no change in dipole moment	417	0	A1'
5	B centre vibrates along y axis	939	259	E'
6	B centre vibrates along the x axis	939	259	E'

As with the case for BH₃, the predicted IR spectrum displays 3 observable peaks despite there being 6 distinct calculated vibrations. Again, this is due to two degenerate sets of vibrations and one non- IR active vibrational mode.

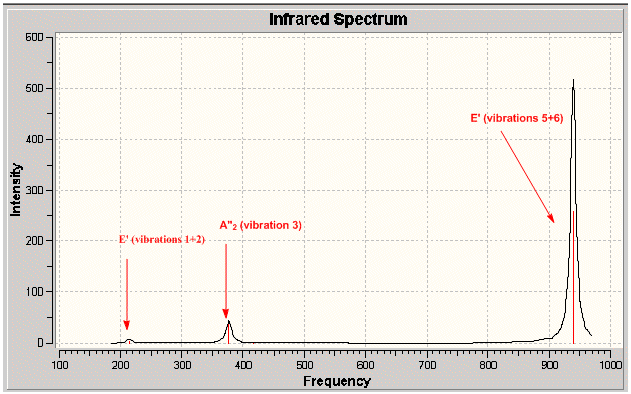
Section 2

Analysis of the cis and trans isomers of Mo(CO)₄L₂

Octahedral Mo(CO)₄(PPh₃)₂ can exist as either the cis or trans geometric isomer. One of which is thermodynamically more stable. A second year lab experiment indicated this to be the trans - isomer, at least in the solid state. Due to the different symmetry of the molecules, IR spectroscopy can be used to differentiate between the two, based on the number of observed carbonyl stretching frequencies.

• Can DFT be used to confirm the relative stabilities of the isomers and to predict the IR spectrum of each isomer?

However, as triphenylphosphine ligands have quite a large degree of conformational flexibility, it would take a significant amount of time to complete the required calculations. Hence, the phenyl groups have been replaced by chlorine groups, which supposedly exhibit similar electronic properties to the phenyl groups. How well this approximation holds will have to be determined.

Geometry optimisation

An initial optimisation of both isomers was performed using the DFT-3BLYP method and the LanL2MB basis set. The optimised geometries of this were then manually changed into the required configuration to ensure that the global minimum (eg. the most stable conformation) was found upon a second optimisation, using the more accurate basis set, LanL2DZ.

Table.?. Key geometrical parameters of both isomers

Parameter	Cis.calc.DOI:10042/to-4478	Cis. Lit	Trans. Calc.DOI:10042/to-4477	Trans. Lit
r(Mo-P) /Å	2.51	2.58	2.45	2.50
< P-Mo-P/°	94	104.62	177	180.00
r(Mo-C(O)) cis	2.06	2.06	2.06	2.02
r(Mo-C(O)) trans	2.01	1.97	-	-
r(CO) cis	1.14	1.17	1.17	1.17
r(CO) trans	1.16	1.18	-	-

N.B Both literature sources refer to Mo(CO)₄(PPh₃)₃ rather than the Mo(CO)₄(PCl₃)₃ studied.

• The calculated P-Mo-P angle in the cis isomer is a lot closer to the ideal octahedral angle of 90° than the actual PPh₃ dervivative. This does not mean that the calculation is poor,but instead indicates that the choice of Cl to replace Ph groups is a poor match in terms of steric contributions. The triphenylphosphine groups, being very bulky, result in a larger deviation away from this ideal angle, to reduce steric interactions.

• In Mo(CO)₄(PPh₃)₃ the two PCl₃ groups are almost perfectly eclipsed relative to one another. In contrast the PPh3 groups in Mo(CO)₄(PCl₃)₃ appear to be staggered in the X-Ray crystal structure. This difference could be due to the larger size of the phenyl groups, such that it is too energetically costly for them to adopt an eclipsed conformation, whereas for the chlorine case this is not so. However, the eclipsed nature of the PCl₃ ligands might explain why they are not quite linear.

• In both the experimental and calculated cases, the Mo-P bond lengthgs for the trans isomer are significantly shorter than those of the cis isomer. Again, this is likely to be due to steric interactions. A shorter bond length results in more clash between the ligands - hence, by increasing the bond length in the cis isomer, these interactions can be minimised. However, Hogarth and Norman argue that the extent to which the Mo-P bond is shortened in the trans isomer cannot be explained by steric factors alone, and suggest that a trans effect is likely to play a role.

• For the cis isomer, the calculation correctly demonstrates that the cis Mo-C bond lengths are longer than those trans. This is probably due to electronic effects (eg. a trans effect). The phospine ligand is an electron donor, donating it's lone pair of electrons into a suitable orbital on the metal centre. Hence the Mo-C bond trans to the PR₃ group is strengthened and therefore, shortened. As the carbonyl group is a good π-backbonding acceptor, it should be expected that if the M-C bond strength increases, that more electron density should be available to be placed into the antibonding π CO orbital, resulting in an increase in the CO bond length. This is what is observed; the trans CO bond lengths are longer than the cis. Comparison to the trans isomer, indicates that trans effect is not affecting the CO bond lengths, as would be expected.

• Overall, the results indicate that chlorine is a reasonable replacement for phenyl in terms of electronic interactions, if not steric bulk.

Relative energies of the isomers

Experimental results indicate that trans Mo(CO)₄(PPh₃)₂ is thermodynamically more stable than it's cis isomer and hence, isomerisation between the two is relaltively easy. The most common explanation for this is that upon isomerisation to the trans isomer, steric interaction between the two bulky phosphine ligands is reduced. Hence, the trans isomer is energetically more favourable.

The calculated results however, indicate that the cis isomer, based on Mo(CO)₄(PCl₃)₂, is energetically more favourable by ~ 2.7 kJmol^-1. As the error for the energy calculation is ~ 10kJmol^-1, the results are by no means conclusive. However, it should be noted that the calculated values are for the gas phase, whereas the experimental results are for solid state at room temperature. Furthermore, DFT energy calulations on a variety of M(CO)4(PR3)2 complexes revealed that in the gas phase, the cis isomer was more stable for all of them, including Mo(CO)₄(PPh₃)₂. As a result they suggest that electronic factors must play an important role in stabilising the cis isomer and that the stability of the trans isomer in the solid state could be due to other factors, rather than steric effects.

Table.? Relative energies of the trans and cis isomers of Mo(CO)₄(PCl₃)₂

	Trans - isomer	Cis- isomer
Energy/ a.u.	-623.57(603)	-623.57(707)

Nevertheless, other evidence does seem to indicate that by changing the nature of the PR₃ ligand, the relative stabilities of the cis and trans isomers can be adjusted. If the steric bulk of the ligand were to be increased the trans isomer would be expected to be more energetically favoured. Furthermore, by increasing bond length and decreasing the 'cone angle' of the ligand, the cis isomer could be made to be less thermodynamically unfavoured.

Running calculations on very bulky ligand is not practical. However, the optimisation of a less sterically demanding complex and comparison to the above results, may reveal whether or not changing the steric bulk affects the thermodynamic properties.

Table.? Relative energies of the trans and cis isomers of Mo(CO)₄(PH₃)₂

	Trans - isomer	Cis- isomer
Energy/ a.u.	-537.43(069)	-537.43(766)

PH₃ is both less sterically demanding than PCl₃ and less electron donating. As with Mo(CO)₄(PCl₃)₂ the results seem to sugest that the cis isomer is more stable in the gas phase, although by a more significant amount, ~-18kJmol^-1, now greater than the error margin of the calculation. PH₃ is both less sterically demanding than PCl₃ and less electron donating. Hence, this would suggest that the relative stabilisation is due to a decrease in steric interactions.

As with BCl₃ and BH₃, before analysis of the above geomtries, a frequency analysis of all isomers was needed in order to confirm that a minimum geometry had been found.

Vibrational analysis

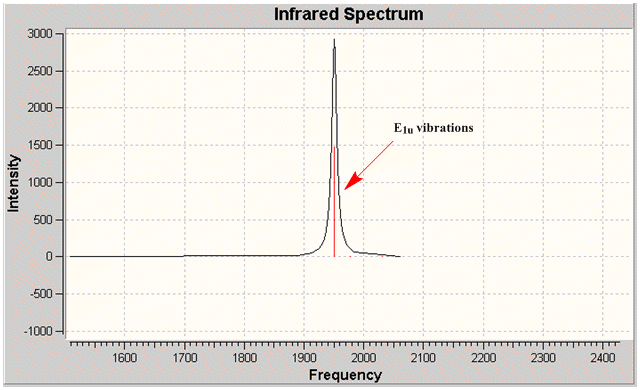
Group theory can be used to predict the number of carbonyl stretches observed for both cis and trans isomers of Mo(CO)₄L₂. If L is assumed to be a point ligand with no symmetry of it's own, then the ideal points of the isomers can be worked out to be C_2v for the cis isomer and D_4h for the higher symmetry trans isomer. Applying group theory (See figures below for method and results), predicts that 4 CO stretches will be observed for the cis isomer and 1 for the trans isomer (only the degenerate E_1u mode is IR active).

Table.?. Vibrational analysis of Cis Mo(CO)₄(PCl₃)₂ DOI:10042/to-4517

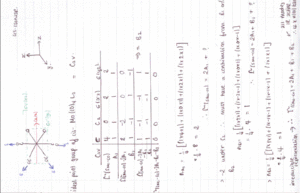
no	Description	Freq./cm-1	Lit. Freq/ cm-1	IR intensity	Symmetry (C2v point group)
1	Asymmetric stretch; 2x cis CO groups in xy plane - one CO bond extends whilst the other compresses	1945	1897	763	B2
2	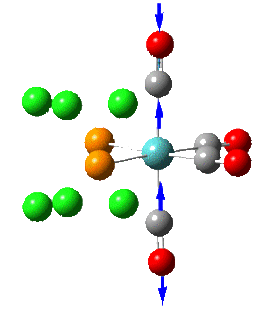Asymmetric stretch; as above but with the trans CO groups	1949	1908	1499	B1
3	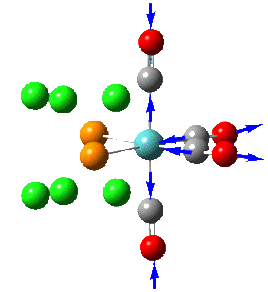Symmetric stretch; 2x trans CO groups compress in phase, 2 x cis CO groups extend in phase	1958	1927	633	A1
4	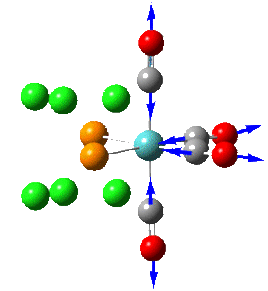Symmetric stretch; all CO groups extend in phase	2023	2023	597	A1

Four distinct carbonyl frequencies have been calculated, in agreement with the prediction for the cis isomer. The differences between the literature and computed values could be partly due to the 10% systematic error associated with the frequency calculation and also due to the different phases in which the molecule is in (eg. gas phase for calculated).

Fig.? Carbonyl stretching region of predicted IR of cis isomer

Table.?. Vibrational analysis of Trans Mo(CO)₄(PCl₃)₂ DOI:10042/to-4516

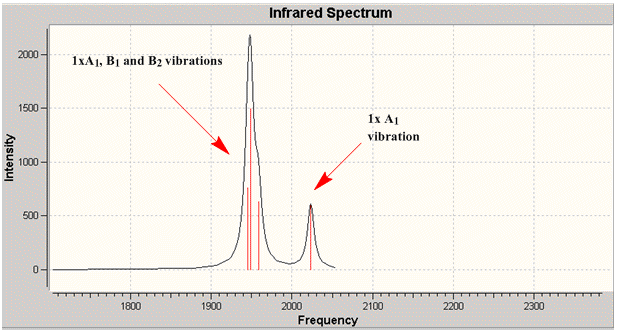
no	Description	Freq./cm-1	Lit . Freq/ cm-1	IR intensity	Symmetry (D4h point group)
1	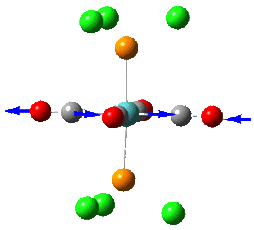Asymmetric stretch; 1x CO extends whilst the other, trans to it, compresses	1950	1901	1475	E1u
2	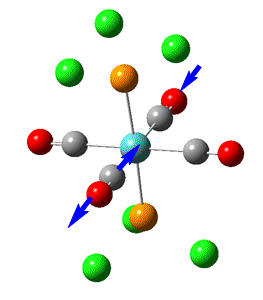Asymmetric stretch; as above but with the other trans CO groups	1951	1901	1467	E1u

The two degenerate E_1u vibrations result in one clear peak typical of the trans isomer. However, when the vibrations are listed in guassview, two more CO stretches were also apparent, with a non-zero IR intensity (albeit so small not observable on the IR spectrum). Although these B₁ and B₂ stretching modes should be non-IR active under ideal D_4h symmetry, the molecule does not quite perfectly fit this 'ideal' symmetry.

Fig.?. Carbonyl stretching region of trans isomer

Two low frequency (eg. <20cm^-1)vibrations are present for each isomer. These low energy vibrations are easily activated at room temperature and hence, the molecule would be undregoing such motions at room temperature.

Tabel?. Low energy vibrations for both isomers

heading	heading
Cis	File:Lowvib1.gif cell	File:Lowvib2.gif cell
Trans	Cl substituents on both ligands twist in the same direction but in the opposite direction to the carbonyl groups around the metal centre	File:Lowvib2b.gif cell

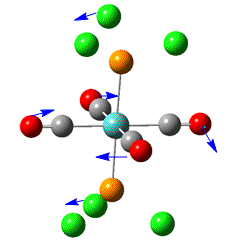Mini Project: Investigation into multiple bonding of heavier elements of group 4, Si and Ge

The heavier group 4 analogues of alkenes and alkynes display a greater variety of structural conformations, dependent on the substituent and size of the group 4 element. Practically, these molecules generally require relatively large subtituents in order to be experimentally isolated, if they can be at all. Computational chemistry, therefore, provides a convenient way in which a wide range of otherwise unobtainable structures of group 14 double and triple bonds can be studied and rationalised.

Final calculations were performed using the B3LYP method and the LanL2DZ pseudo potential and basis set, including the 'extra basis' to take into account the dAO functions (as heavier elements are being studied).

A 2001 literature example found, based on the DFT study of Germanium and Tin triple bonds also chose to use the B3LYP method but opted for the 3-21G* basis set, based on the size of the substituents they were using and the fact that upon comparison to use of a higher basis set, results showed minimal deviation.

The choice of method/ basis set used here therefore seems reasonable.

Following an initial 'loose' optimisation with the LanL2MB psuedo potential/basis set, a second optimisation using the more accurate LanL2DZ basis set and a tighter convergence was used. Frequency calculations (see earlier section for explantion of this) were performed for each optimised structure to confirm whether or not a minimum energy conformation had been found. If significant negative vibrations were obsereved, the structure was manually adjusted and re-optimised until a minimum energy confrormation was found.

Double bonds: Disilenes and Digermenes

Fig.? CGMT model for double bond formation

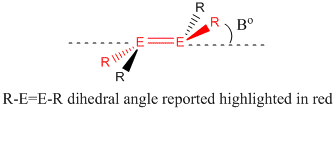
Alkenes are generally always planar structures, but deviations away from planarity occurs when carbon is replaced by a heavier group 4 element. Thus, disilenes commonly exhibit trans bending and/ or twisting. Why? Use of the CGMT model (Fig.?) is helpful in demonstrating how the carbene/ silene fragments combine in order to form a double bond. For carbenes, the triplet state is generally the ground state electronic configuration (for carbenes bearing large, electropositve substituents - Bent's rules), hence direct head on overlap of 2x singly occupied p orbitals, to form a σ bond, and side on overlap of the 2x singly occupied p orbitals results in formation of a planar double bond. In contrast, the singlet state of a silene is generally more stable. Combination of 2 x singlet silene fragments results in a trans bent structure. For a planar structure to form, excitation to the higher energy triplet state would be required. If the energy for this promotion was not recouped by the formation of a double bond, the formation of a 'classical' double bond, would not occur

How does trans bending and twisting affect the HOMO-LUMO energy gap?

Experimentally, evidence for these deviations away from a planar structure can be obtained by performing a UV-Vis absorption analysis eg. the different structures appear different colours. This is due to the change in ΔE between the HOMO and LUMO MOs upon distortion away from planarity. As fig.?. demonstrates, increasing the transbent angle, β, decreases the enegry gap w.r.t the planar conformation. Increasing the twist angle towards 90°,results in the HOMO and LUMO orbitals moving towards degeneracy.

Fig.? Change in relative HOMO-LUMO energy difference with change in trans bent and twist angles. Figure taken directly from Dr. D. Scheschkewitz's 3rd year Advanced Main Group notes

Use of DFT calculations to investigate the following:

• How does substituent size effect the conformation?

- By changing the size of the substituent, how will the conformation about the E=E double bond change? - Compare results between 4x methyl substituents and 4x larger R groups (N.B although a very bulky substituent would be better in terms of comparison, the degree of conformational flexibility/computational time wuld be high, hence a smaller R group was chosen).

• How does increasing the group 4 element from silicon to germanium effect the conformation?

• Does MO analysis support literature predictions?

- How does a change in conformation affect the HOMO-LUMO gap? -Will the resulting trans- bent MOs show the expected deviations away from the ideal π orbital?

R group	Parameter definition

Table.?. Comparison of structures

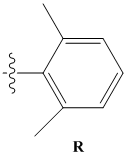Parameter	Si2Me4	Si2R4	Ge2Me4	Ge2R4
Description	Trans bent	Almost planar	Trans bent	Trans bent and twisted
r(E=E)/Å	2.17	2.16	2.64	2.67
R-E=E-R /° /	180.0	178.2	180.0	173.9
β/°	16	0.9	28	28
Final optimisation DOI	DOI:10042/to-4567	DOI:10042/to-4568	DOI:10042/to-4571	DOI:10042/to-4573
Vibration DOI	DOI:10042/to-4569	DOI:10042/to-4570	DOI:10042/to-4572	DOI:10042/to-4572

• All structures, except Si₂R₄, show the expected trans - bent conformation.

-Although for very large/bulky substituents a planar conformation may be adopted (they can potentially stabilise the triplet state, the R group used here is not realistically large enough to do so. It is therefore more likely that the global minimum optimised structure has not been found. As R₂Si=SiR₂ is known to have a shallow potential surface, relative to R₂C=CR₂, there may only be a small difference in energy between the planar and trans-bent structures.

• Upon going from Si₂Me₄ to Ge₂Me₄ there is an increase in the trans-bent angle. This could possibly be due to steric reasons or possibly the relative degree bending that is requred in order for a double bond to form is greater for heavier elements.

• Comparison of Ge₂Me₄ to Ge₂R₄ shows that instead of favouring a planar conformation, the bulkier ligand results in twisting about the central Ge=Ge bond. The bond length is also slightly longer, a would be expected for an increase in substituent size.

• Visually, it can be seen that a small trans - bent angle of 15° does not result in a significant change to the π bonding MO. A larger trans bent angle of 28°, as seen for the Germanium examples results in a more noticable, but still quite small change.

Can MO analysis be used to support the above observations?

• On increasing the trans - bent angle on going from Si2Me4 to Ge2Me4 there is a corresponding decrease in the HOMO-LUMO ΔE. However, whether or not Si and Ge examples can be compared directly is uncertain.

• Both Ge₂Me₄ and Ge₂R₄ have the same trans bent angle. However, Ge2R4 has a smaller HOMO-LUMO ΔE. This could be due to the degree of twisting which it displays but arguably, the change in substituents would also effect the ΔE value

Therefore, in order to gain a more reliable view of how conformational change results in corresponding MO changes, the effect of changing the dihedral angle between two substituents cis to one another on Si₂Me₄ was looked at.

Table.? MO analysis

	Si2Me4	Si2R4	Ge2Me4	Ge2Ph4
HOMO-LUMO energy/a.u	0.142	0.123	0.107	0.092
HOMO	cell	cell	cell	cell
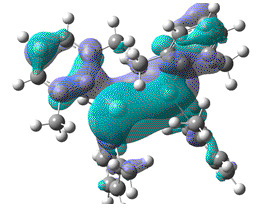MO DOI	DOI:10042/to-4591	DOI:10042/to-4590	DOI:10042/to-4589	DOI:10042/to-4588

Direct comparison between the results listed below can be made.

• It is evident that a larger degree of distortion between the two Si2Me2 fragments does result in a decrease in the HOMO-LUMO ΔE, in agreement with literature predictions.

• Furthermore, the effect that this distortion has on the MO, resulting from the overlap of 2x pz AOs, can be more clearly seen. In order to show that upon forming a twist angle of 90°, the HOMO and LUMO orbitals become degenerate, rotation about the central Si=Si bond, with one fragment fixed in place should have been studied.

Effect of changing dihedral angle on MOs for Si₂Me₄

Dihedral angle	0°	30°	60°	90°	180°
HOMO-LUMO energy/ a.u	0.158	0.144	0.130	0.115	0.063
HOMO
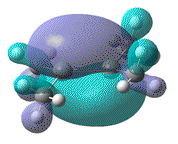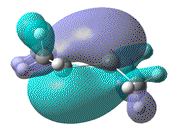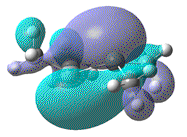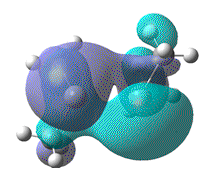MO DOI	DOI:10042/to-4624	DOI:10042/to-4626	DOI:10042/to-4612	DOI:10042/to-4627	DOI:10042/to-4625

Triple bonds: Disilynes and Digermynes

Upon descending group 4, the heavier analogues of alkynes are expected to show significant trans- bending and a decrease in bond order. As fig.? demonstrates, there are several possible ways, based on resonance structures, of best describing the bonding nature of the silicon and germanium analogues.

• Can DFT be used to demonstrate:

- the change in the trans bent angle on going from silicon to germanium?

- the change in the trans bent angle on changing the substituent size?

- Will NBO charge analysis reveal which desription of bonding best describes the studied examples?

Fig.?. Change in bond order w.r.t GIV element size. Figure taken directly from Dr. D. Scheschkewitz's 3rd year Advanced Main Group notes

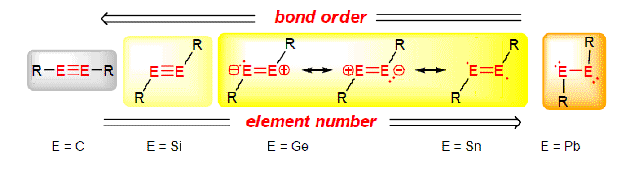
Measured angle

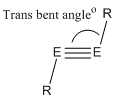N.B. In the following description, an increase in the trans- bent angle (see above) equates to DECREASE in trans bending.

• Upon going from E₂R₄ to E₂R₂ there is a decrease in bond length , particulary for the Germanium case. This indicates that the structures do have a degree of triple bond character. Comparison of Ge₂R₂ to a literature example of Ge₂Tbt₂ with a bond length of 2.231Å, indicates that the calculated bond lengths show reasonable agreement with literature values.

• Upon going from Silicon to Germanium there is a clear increase in the trans bendng, also in agreement with literature findings (lit. values for Tbt2Ge2 and TbtSi2; 121.8° and 130.9° respectively).

• In contrast, increasing the size of the substituent decreases the trans bending, and also increases the bond length. However, as the R group is aryl, it could be argued that it has a greater preference to be more linear - greater ability for delocalisation across the molecule.

Table.? Conformation analysis

	Si2Me2	Si2R2	Ge2Me2	Ge2R2
r(E-E)/Å	2.11	2.12	2.28	2.30
θ/°	131.5	134.9	127.6	130.5
Final optimisation DOI		DOI:10042/to-4595	DOI:10042/to-4592	DOI:10042/to-4594

• Although NBO analysis is by no means conclusive, for three of the cases the charges on the central group 4 elements, for each individual molecule, were the same . In contrast, Ge₂Me₂ shows a slight difference in the respective charge on the two Ge atoms. Although, this may be error within the calculation, it could possibly indicate that a more dipolar description of this molecule may be appropriate, in contrast, perhaps, to a radical desription of the other cases.

Table.? MO/ NBO analysis

	Si2Me2	Si2R2	Ge2Me2	Ge2R2
NBO charge on E/	0.345	0.394	Ge(1) = 0.373 Ge(2)=0.360	0.424
HOMO
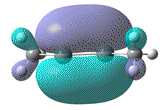MO DOI	DOI:10042/to-4611	DOI:10042/to-4610	DOI:10042/to-4609	DOI:10042/to-4608

A look at the HOMO-1 MO of Si₂Me₂, suggests that it is formed from overlap of 2x py AOs and does indicate a larger and equal amounts of electron density on sites where a radical elctron may be expected to occupy. Whether or not this is speculation, it does perhaps explain the triple bond character.

Homo-1 MO of Si₂Me₂

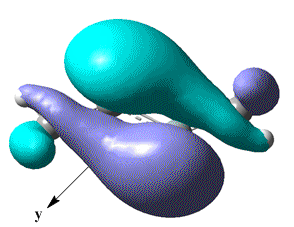
Unfortunately mini project is not quite complete (ran out of time).