Rep:Mod1:zy909
Molecular Mechanics
Molecular mechanics is an empirical approach to geometry optimisation in chemical systems, employing a parametric force field that determines the steric strain associated with any conformer. This is coupled to an optimiser that adjusts molecular conformations to minimise this steric energy.
The force field employed is based on empirical parameters defined for each pair or set of atoms. The popular MM2 force field developed by Allinger[1] has proven to be a robust and reliable method for modelling hydrocarbon skeletons, and includes the following factors:
- Bond lengths
- Bond angles (triatomic)
- Dihedral angles (torsion)
- Van der Waals interactions (through-space interactions)
- Dipole-dipole interactions (electrostatic)
For example, the ideal C-C single bond length is defined based on actual bond lengths in a wide variety of molecules; any deviation from this ideality contributes to the total strain energy of the molecule. Bond lengths and angles are modelled as harmonic oscillators, with the ideal length and angle corresponding to an energy minimum; dihedral angles are modelled analytically using a cosine relation; Van der Waals interactions are simulated using a 6-12 Lenard-Jones potential; while dipole-dipole interactions are modelled by classical electrostatics.
Further developments in molecular mechanics include larger parameter sets or additional factors that improve the correlation between experimental and theoretical results, and include the MM3[2] and MM4[3] force fields. Another line of development involves the modelling of large macromolecules such as proteins and DNA, for which the speed and computational simplicity of the method proves superior to slower ab initio methods, and include the AMBER[4], CHARMm[5] and OPLS[6] force fields.
However, molecular mechanics methods are limited to the modelling of stable molecules, as the empirical parameters are derived from known compounds. Any large deviation from this knowledge base, in modelling particularly strained systems or reaction transition states, falls outside the capabilities of such methods and cannot be simulated accurately. Furthermore, the simulated Van der Waals interactions are at best crude representations of non-bonded, through-space interactions, the full complexity of which can only be handled by quantum mechanical methods. These challenges are encountered in the course of this computational chemistry module, and throughout the rest of the report, it will be pointed out where these limitations arise, and how semi-empirical or fully ab initio quantum mechanical methods are used as more accurate representations.
Hydrogenation of Cyclopentadiene Dimers
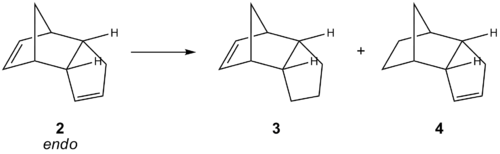
Cyclopentadiene dimerises on standing through a Diels-Alder reaction. Of the two possible isomers, only the endo isomer 2 is found to be formed experimentally. This reaction is studied with an MM2 model, which shows that the exo isomer 1 is the thermodynamic product, indicating that the reaction must be operating under kinetic control.
Further to this, the hydrogenation products of the cyclopentadiene dimer are modelled with MM2, indicating that the two possible hydrogenation isomers differ significantly in energy, due to differences in ring strain.
Dimerisation
The MM2 calculations show that the exo product 1 is thermodynamically more stable, as would be expected from simple steric considerations[7], due to the greater torsional strain from eclipsed interactions. With the exo product 1, ring A (blue - see structure) is eclipsed with a one-carbon bridge, whereas in the endo product 2, ring A (blue) is eclipsed with a two-carbon bridge. This explanation is supported by the MM2 calculations, which show that the difference in isomer energies is due primarily to differences in torsional strain.
As the endo product 2 is formed despite being less stable thermodynamically than the exo product 1, the dimerisation reaction must be operating under kinetic control, with a lower transition-state energy barrier for the reaction pathway to endo product 2. This selectivity is due to favourable secondary orbital interactions in the transition-state leading to the endo product[7], a key factor which is not modelled by molecular mechanics calculations, hence limiting its utility in predicting reaction products.
| Isomer | Energy / kcal mol-1 | |||||||
|---|---|---|---|---|---|---|---|---|
| Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VdW | 1,4 VdW | Dipole-Dipole | Total | |
| Exo isomer 1 | 1.29 | 20.58 | -0.84 | 7.66 | -1.42 | 4.23 | 0.38 | 31.88 |
| Endo isomer 2 | 1.25 | 20.84 | -0.84 | 9.51 | -1.55 | 4.33 | 0.45 | 33.99 |
Hydrogenation
The calculations show that isomer 3 is less stable than 4, due to the higher angle strain in 3. Comparing both isomers, the only difference is that 3 has a double-bond in a bicyclo[2.2.1] system composed of a 5-membered ring and a 6-membered ring, while 4 has its double bond in a 5-membered ring. It is expected that placing a double bond (with its enforced increase in bond angles) in a bicyclic ring system would introduce a greater degree of ring strain (isomer 3), as compared to a double bond in a monocyclic ring system (isomer 4); this prediction is borne out by the calculations, which largely attribute the greater steric energy of 3 to angle strain.
| Isomer | Energy / kcal mol-1 | |||||||
|---|---|---|---|---|---|---|---|---|
| Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VdW | 1,4 VdW | Dipole-Dipole | Total | |
| Isomer 3 | 1.23 | 18.93 | -0.76 | 12.13 | -1.50 | 5.73 | 0.16 | 35.92 |
| Isomer 4 | 1.10 | 14.51 | -0.55 | 12.50 | -1.05 | 4.51 | 0.14 | 31.16 |
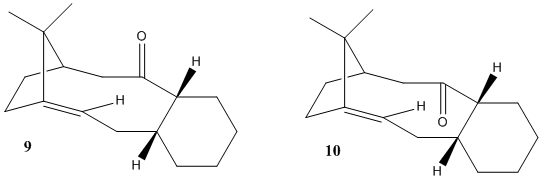
Stereochemistry of an Intermediate in the Synthesis of Taxol
Atropisomerism is a special case of optical isomerism caused by restricted rotation about single bonds, such that the energy barrier to interconversion is high enough to allow separation and isolation of unique conformers or atropisomers[8].
In the case of the isomeric forms of the Taxol intermediate synthesised by Paquette through an oxy-cope rearrangement[9], intermediate 9 is the only isomer formed; the carbonyl group isomerises to the down position, as in intermediate 10, upon epoxidation of the bridgehead alkene. An analogous oxy-cope rearrangement producing the intermediate with a dithiolane group on the cyclohexane ring also formed initially the isomer with carbonyl moiety pointing up (corresponding to isomer 9), and isomerised to the down-isomer (corresponding to 10) upon refluxing in THF[10]. This evidence suggests that the up isomer 9 is the kinetic product of the reaction, enforced by the stereochemistry of the pericyclic transition state, whereas isomer 10 is the thermodynamic product and should be more stable. In accordance with this experimental evidence, the down isomer 10 is indeed calculated to be thermodynamically more stable than the up isomer 9, using both the MM2 and MMFF94 models.
| Isomer | MM2 Energy / kcal mol-1 | MMFF94 Energy / kcal mol-1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VdW | 1,4 VdW | Dipole-Dipole | Total | |||
| Carbonyl Up Isomer 9 | Twist-Boat | 2.79 | 16.57 | 0.44 | 20.58 | -0.35 | 13.90 | 0.17 | 54.10 | 77.88 |
| Chair | 2.68 | 15.84 | 0.40 | 18.23 | -1.07 | 12.66 | 0.15 | 48.89 | 70.53 | |
| Carbonyl Down Isomer 10 | Twist-Boat | 2.64 | 11.15 | 0.30 | 21.92 | -1.26 | 13.59 | -0.19 | 48.15 | 66.28 |
| Chair | 2.55 | 10.70 | 0.32 | 19.74 | -1.40 | 12.55 | -0.18 | 44.28 | 60.54 | |
Intermediate 10 belongs to the class of hyperstable olefins, first defined by Maier and Schleyer[11] in systems of bridgehead olefins. Hyperstable olefins are found to be less reactive than typical olefins, owing to the unusual situation of having less ring strain than the parent olefin - this manifests in a resistance to hydrogenation[12][13] and other reactions.
Hyperstable olefins are defined as olefins with a lower strain energy (as calculated by molecular mechanics methods) than their parent alkanes[13]. Although molecular mechanics results are generally not directly comparable for molecules with different sets of atoms and bonds, in this case, as the force field calculations differ only at the olefinic site, the difference in calculated strain energies may be taken as a proxy for the hydrogenation process[11]. Nevertheless, this strain energy difference does not equate to the heat of hydrogenation.
| Compound | MM2 Energy / kcal mol-1 | |||||||
|---|---|---|---|---|---|---|---|---|
| Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VdW | 1,4 VdW | Dipole-Dipole | Total | |
| Alkene 10 | 2.55 | 10.70 | 0.32 | 19.74 | -1.40 | 12.55 | -0.18 | 44.28 |
| Alkane 11 | 2.64 | 11.75 | 0.57 | 22.69 | -1.98 | 15.17 | 0.00 | 50.84 |
In investigating the phenomenon of hyperstability, intermediate 10 is preferred over 9, as it is the thermodynamically more stable isomer. The MM2 calculations show a negative olefin strain energy of -6.56 kcal mol-1 with respect to the parent alkane 11, indicating that 10 is another example of a hyperstable olefin. As expected from the theory, the difference in strain energy is mostly due to torsional (dihedral) strain and 1,4 Van der Waals interactions. The torsional strain and 1,4 Van der Waals strains may be attributed to the two additional hydrogen atoms in 11, which are locked by the ring to take a 29° dihedral angle, deviating from the ideal 60° angle. In addition, a second 1,4-dihedral angle is reduced from the near-ideal 63° in alkene 10 to a more highly strained 10° in alkane 11.
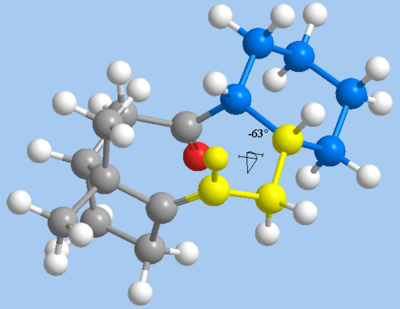
|
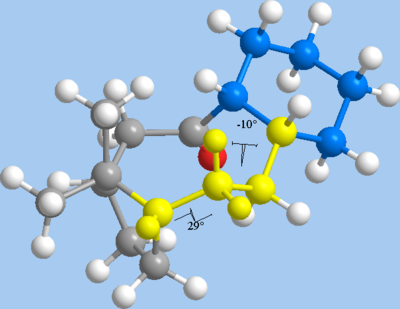
|
| Near-ideal dihedral angle in alkene 10 | Torsional strain and unfavourable 1,4 VdW interactions in alkane 11 |
Interestingly, despite the unfavourable transannular (non-1,4 Van der Waals) interaction arising from a H-H close contact of 1.9Å in 11, this strain is not reflected in the MM2 calculations (the same transannular distance is a more favourable 2.2Å in alkene 10). Non-bonded H-H Van der Waals interactions are increasingly repulsive under 2.4Å, so this should be extremely unfavourable, yet the non-1,4 Van der Waals strain energy is actually more favourable for 11 than for 10.

|
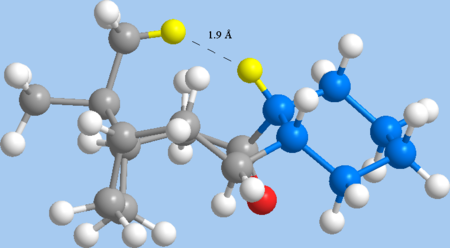
|
| Minimal transannular interaction in alkene 10 | Strongly unfavourable transannular strain in alkane 11 |
Semi-Empirical Methods
Regioselectivity of Nucleophilic Addition to an Alkene

|
|
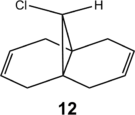
Compound 12 (visualise) demonstrates regioselective electrophilic addition by dichlorocarbene or peracid to give the trichloride 13 or epoxide 14 respectively[14]. The regioselectivity demonstrated here is two-fold: electrophilic addition occurs solely on the alkene endo to chlorine (regioselectivity), and on the face opposite the chlorine atom (π-facial stereoselectivity). These results were rationalised by semi-empirical PM3 calculations and X-ray crystallographic studies[15], which show a stabilising interaction between the πexo C=C and σ*C-Cl orbitals that reduces the nucleophilicity of the exo-alkene.
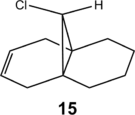
This study is repeated using the improved PM6 method, reaching the same overall conclusions. However, the ordering of molecular orbital by energy differs from that derived by PM3. Compound 12 was first optimised by MM2, before minimisation with PM6. However, the molecular orbitals obtained through this procedure were unsymmetrical and did not match those in the literature[15], as mathematical errors in optimisation had erased the symmetry in the molecule. As such, the molecule was symmetrised (Cs) and optimised with B3LYP/6-31G(d,p); this was then subjected to a PM6 minimisation to obtain the MOs shown below. The alkene 15 (visualise), used as a comparison in the vibrational frequency analysis, was similarly optimised by B3LYP/6-31G(d,p).
Molecular Orbital Analysis
As 12 is being subjected to electrophilic attack, the HOMO is the relevant orbital in considering reactivity. From the diagram, it is clear that the endo-alkene has the largest orbital coefficients in HOMO, and is therefore the most nucleophilic site. In contrast, it is the HOMO-1 where the exo-alkene is has its largest orbital coefficients, indicating that the π-system of the exo-alkene is stabilised. This is likely due to mixing with the LUMO+1, which is characteristic of the σ*C-Cl bond; indeed, the HOMO-1 shows the exo-alkene π-system being delocalised towards the C-Cl group. As such, a frontier molecular orbital consideration supports the observation of attack at the endo-alkene.
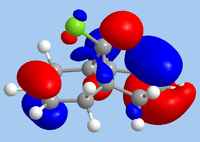
|
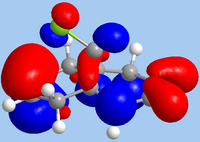
|
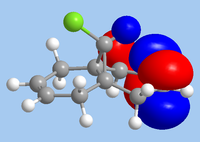
|
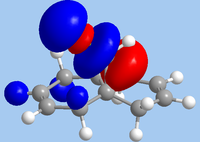
|
|
| HOMO-1 | HOMO | LUMO | LUMO+1 | LUMO+2 |
Although the selectivity for the face opposite the chlorine atom has not been explained in the literature, this can be easily rationalised by steric and electronic factors. In terms of sterics, approach by the electrophile is impeded by the chlorine atom, generating a preference for anti-attack. Furthermore, in the HOMO, the nCl-πC=C interaction results in destructive interference on the syn-face of the alkene, reducing electron density and thus favouring electrophilic attack on the opposite anti-face.
Vibrational Frequency Analysis

|

|
This phenomenon is further explored by considering compound 15, where the exo-alkene in 12 has been hydrogenated. By removing the σ*C-Cl-πC=C interaction, the C-Cl bond should be strengthened, which should manifest as a higher frequency for the C-Cl stretching mode. As expected, the C-Cl stretching frequency is lower in the diene 12, reflecting the weaker C-Cl bond resulting from electron donation by the exo-alkene into the σ*C-Cl orbital. In contrast, the endo-alkene, which is not directly affected by the hydrogenation, retains the same vibrational frequency in both molecules.
| Compound | Frequency / cm-1 | ||
|---|---|---|---|
| C-Cl stretch | Exo C=C stretch | Endo C=C stretch | |
| Diene 12 / SPECTRa | 771 | 1737 | 1757 |
| Alkene 15 / SPECTRa | 775 | - | 1758 |
Neighbouring Group Participation in Glycosidation
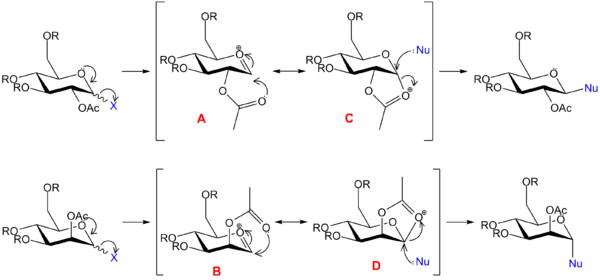
In the glycosidation reactions of sugars protected with an ester at the 2-OH, neighbouring group participation by the ester carbonyl stabilises the oxonium intermediate and gives rise to 1,2-trans substituted sugars. This is a non-bonded, through-space interaction, and is ideally modelled by semi-empirical or ab initio quantum mechanical methods. Nevertheless, to test the limits of molecular mechanics, a comparison is made between the MM2 and PM6 methods in modelling the oxonium species A - D. To minimise the computational demands, methyl groups are used to represent the generic alkyl R groups.
|

|
| cis ring junction, A | trans ring junction, A’ |
Structure Optimisation
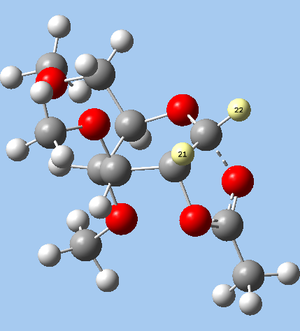
The oxonium intermediates were first optimised by MM2 methods. For A and B, the C=O double-bond within the 6-membered ring forces it to take on either of two twist-boat conformations. Conformations with the 3- and 4-OR in axial positions are found to be energetically preferable to conformations with equatorial OR groups, so this low-energy conformation is modelled for both A and B. Two conformers are possible for each of A and B, depending on whether the new 5-membered ring is fused to the existing 6-membered ring in a cis (isomers A and B) or trans (isomers A’ and B’) relationship. For all 4 possible species (A, A’, B, B’), the carbonyl group of the 2-OAc is oriented towards the oxonium intermediate, as this reduces strain energy through a stabilising charge-dipole interaction. Dihedral angles were optimised where possible using a dihedral driver, except in the case of the 6-OR group. In this case, it was noted that even greater stabilisation could be brought about by orienting the 6-OR towards the oxonium group. However, this hampered the interaction between the 2-OAc and the oxonium, hence opposing the formation of C and D. For consistency, the 6-OR group is oriented away from the oxonium group in all geometries. For C and D, the number of possible conformers is reduced by the fused ring junction. However, two distinct conformers can be identified for each of C and D, corresponding to their partner conformers A and B respectively.
The MM2-optimised geometries were then subject to a PM6 minimisation, which in the case of species A and B brought the 2-OAc carbonyl groups much closer to the oxonium ion. Geometry minimisations were first carried out until the RMS of optimisation fell below 0.1; the resulting structures were then further optimised till an RMS of 0.0001.
The differences in distance between the 2-OAc carbonyl and the oxonium group (O--C=O distance) reflect the characteristics of each method. In the case of A and B, the MM2 distance is an overestimate, failing to account for the stabilising orbital interactions that favour a closer distance; PM6 takes these into account, and gives a much closer bond distance for all A and B conformers. In contrast, for C and D, MM2 underestimates the bond distance, modelling a bond distance of 1.4Å for all C and D conformers, a result that reflects the empirical basis of the MM2 model.
For reference, the conformers of A and B were optimised by B3LYP/6-31G(d,p). The resulting geometries obtained were very similar the PM6 structures, indicating that PM6 is sufficiently accurate for this system. An exception was A', for which the optimised DFT structure did not show a stabilising interaction between the ester carbonyl and oxonium groups (highlighted in red), indicating that the PM6 geometry of A' is potentially imperfect.
| Species | Ring junction | Model | O--C=O+ distance / Å |
|---|---|---|---|
| A | cis | MM2 | 2.51 |
| PM6 | 1.60 | ||
| DFT SPECTRa |
1.59 | ||
| A' | trans | MM2 | 3.06 |
| PM6 | 2.75 | ||
| DFT SPECTRa |
3.75 | ||
| B | cis | MM2 | 2.65 |
| PM6 | 1.61 | ||
| DFT SPECTRa |
1.64 | ||
| B' | trans | MM2 | 3.16 |
| PM6 | 2.74 | ||
| DFT SPECTRa |
2.77 | ||
| C | cis | MM2 | 1.40 |
| PM6 | 1.60 | ||
| C' | trans | MM2 | 1.41 |
| PM6 | 1.53 | ||
| D | cis | MM2 | 1.41 |
| PM6 | 1.58 | ||
| D' | trans | MM2 | 1.40 |
| PM6 | 1.59 |
Thermodynamic Considerations
From the thermodynamic and bond-distance data, it is obvious that the species with cis ring junctions (A - D) are more stable energetically than the trans analogues (A' - D'), with both MM2 and PM6 models returning the same qualitative results. A visual comparison of cis and trans conformers reveals that the carbonyl moiety of the 2-OAc group can approach the oxonium group more closely in the cis conformer, giving rise to a better stabilising interaction.
This provides a rationalisation for the diastereoselectivity in glycosidation: neighbouring group participation by the 2-OAc group leads to intermediates C and D, with cis-5,6 ring junctions, via A and B respectively, as these are the lowest energy intermediates. Ring-opening of the transient 5-membered ring then occurs by backside nucleophilic attack, giving trans-1,2 products.
| Species | MM2 Energy / kcal mol-1 | PM6 ΔHf / kcal mol-1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VdW | 1,4 VdW | Charge-Dipole | Dipole-Dipole | Total | ||
| A | 2.69 | 11.91 | 1.01 | 2.69 | 0.87 | 19.22 | -31.32 | 8.58 | 15.65 | -91.65 |
| A' | 2.18 | 10.96 | 0.83 | 1.18 | -1.80 | 18.93 | -17.53 | 6.25 | 21.00 | -77.42 |
| B | 2.21 | 11.09 | 0.88 | 2.33 | -2.26 | 19.57 | -20.37 | 6.89 | 20.34 | -88.73 |
| B' | 2.16 | 10.63 | 0.79 | 1.47 | -1.75 | 19.18 | -14.30 | 5.67 | 23.85 | -77.51 |
| C | 1.92 | 12.07 | 0.69 | 8.01 | -3.68 | 18.04 | -6.46 | -1.13 | 29.36 | -91.66 |
| C' | 2.69 | 17.89 | 0.84 | 8.08 | -2.42 | 19.32 | -3.99 | -0.05 | 42.36 | -66.88 |
| D | 1.76 | 13.97 | 0.56 | 6.82 | -4.76 | 18.50 | -0.54 | -0.07 | 36.24 | -84.08 |
| D' | 2.59 | 16.64 | 0.72 | 6.94 | -2.70 | 19.39 | -3.10 | -0.88 | 39.60 | -66.73 |
While both MM2 and PM6 methods arrive at the same qualitative conclusion that the cis conformers are energetically preferred, the PM6 method gives much more realistic geometries that are not inferior to those obtained by ab initio methods. PM6 is therefore be preferred to MM2, which would be useful only for preliminary optimisation. Moreover, as molecular complexity increases, PM6 is likely to consistently return more accurate energies, whereas MM2 may not be able to handle systems more complex than these.
Ab-Initio Methods
Radical Cyclisation in the Total Synthesis of (-)-Maoecrystal Z
A total synthesis of (-)-Maoecrystal Z has been reported, with the key step being a samarium (II) iodide mediated radical cyclisation, simultaneously forming 2 rings and 4 stereocentres with impressive diastereoselectivity[16].
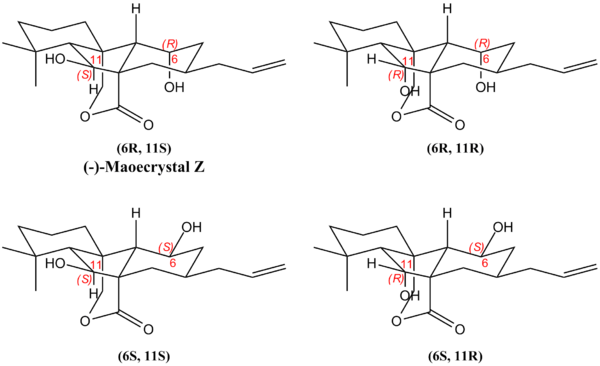
This reaction was chosen for investigation because of its elegance and because the rigidity of the tetracyclic carbon skeleton simplifies NMR prediction by limiting the number of conformers that must be considered. Steric considerations permit a straightforward assignment of the bridgehead carbon stereocentres, as tethering of the aldehyde groups to the carbon skeleton directs attack of each group to opposite prochiral faces of the alkene. This leaves the two alcohol alpha carbons as potentially ambiguous - with a total of 4 possible stereoisomers, the structural assignment of the experimental product as the (6R,11S) stereoisomer is re-examined by comparison with predicted 13C-NMR obtained from DFT-GIAO calculations.
Structure Optimisation
The structures were first optimised by MM2 and then PM6 (RMS < 0.0001). For all 4 possible stereoisomers, the most stable conformers were those with both cyclohexyl rings in chair conformations. As the δ-lactone and cyclopentyl rings are conformationally locked, the obtained structures can be safely assumed to lie on the global minimum of their respective potential energy surfaces. Finally, the geometries were optimised by MPW1PW91/6-31G(d,p), as the MPW1PW91 has been tested and found to be superior for NMR prediction.
NMR Prediction
The experimental and predicted NMR data are summarised in the following table, with deviations greater than 5.0 ppm highlighted in red.
| Experimental | Predicted | Assignment | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (6R,11S) SPECTRa | (6R,11R) SPECTRa | (6S,11S) SPECTRa | (6S,11R) SPECTRa | ||||||
| δ | Δδ | δ | Δδ | δ | Δδ | δ | Δδ | ||
| 176.2 | 172.9 | 3.3 | 169.7 | 6.5 | 169.5 | 6.7 | 168.2 | 8.0 | Lactone C=O |
| 136.6 | 135.4 | 1.2 | 135.1 | 1.5 | 135.5 | 1.1 | 135.4 | 1.2 | Alkene -C=CH2 |
| 116.3 | 114.3 | 2.0 | 114.5 | 1.8 | 114.0 | 2.3 | 114.1 | 2.2 | Alkene -C=CH2 |
| 78.5 | 73.1 | 5.4 | 78.4 | 0.1 | 73.9 | 4.6 | 77.5 | 1.0 | Alcohol; C-11 |
| 74.0 | 72.0 | 2.0 | 71.8 | 2.2 | 70.4 | 3.6 | 70.8 | 3.2 | Lactone δ-C |
| 72.2 | 66.7 | 5.5 | 66.3 | 5.9 | 68.2 | 4.0 | 68.0 | 4.2 | Alcohol; C-6 |
| 66.1 | 64.9 | 1.2 | 58.5 | 7.6 | 64.5 | 1.6 | 59.6 | 6.5 | |
| 54.4 | 56.2 | 1.8 | 56.1 | 1.7 | 57.2 | 2.8 | 58.5 | 4.1 | Lactone β-C |
| 51.5 | 52.9 | 1.4 | 55.8 | 4.3 | 56.1 | 4.6 | 57.1 | 5.6 | Lactone α-C |
| 42.9 | 44.4 | 1.5 | 43.9 | 1.0 | 44.4 | 1.5 | 44.2 | 1.3 | Lactone γ-C |
| 41.6 | 43.5 | 1.9 | 43.3 | 1.7 | 44.3 | 2.7 | 44.2 | 2.6 | |
| 41.1 | 41.3 | 0.2 | 42.6 | 1.5 | 43.4 | 2.3 | 43.2 | 2.1 | |
| 41.0 | 40.4 | 0.6 | 40.5 | 0.5 | 41.1 | 0.1 | 42.7 | 1.7 | |
| 34.0 | 34.3 | 0.3 | 37.5 | 3.5 | 36.2 | 2.2 | 37.6 | 3.6 | |
| 32.7 | 34.1 | 1.4 | 35.4 | 2.7 | 34.0 | 1.3 | 36.7 | 4.0 | |
| 32.6 | 33.7 | 1.1 | 35.1 | 2.5 | 33.9 | 1.3 | 35.6 | 3.0 | |
| 32.2 | 32.6 | 0.4 | 32.3 | 0.1 | 33.3 | 1.1 | 34.2 | 2.0 | |
| 28.2 | 29.1 | 0.9 | 29.8 | 1.6 | 32.5 | 4.3 | 32.0 | 3.8 | |
| 21.3 | 21.9 | 0.6 | 23.3 | 2.0 | 21.8 | 0.5 | 23.5 | 2.2 | |
| 19.3 | 21.2 | 1.9 | 21.3 | 2.0 | 21.1 | 1.8 | 21.2 | 1.9 | |
| Total | 34.6 | 50.7 | 50.4 | 64.2 | |||||
| Average | 1.73 | 2.54 | 2.52 | 3.21 | |||||
The experimental NMR spectrum most closely matches the predicted spectrum of the (6R,11S) isomer, having a lower average deviation than the other possible isomers, supporting the literature structural assignment. In particular, the key lactone C=O and alkene chemical shifts match the literature spectrum particularly well, as compared to the other isomers. However, it is noteworthy that with the assigned (6R,11S) isomer, the chemical shifts of the alcohol α-carbons deviate significantly from experiment, highlighting a key limitation of the exercise.
Conclusion
In summary, 13C-NMR prediction was used to validate the structural assignment of the key Maoecrystal intermediate as the (6R,11S)-isomer, proving the utility of the ab initio DFT-GIAO approach using MPW1PW91/6-31G(d,p) to predict NMR chemical shifts from first principles. Given more time, further supporting evidence for the structural assignment could be obtained by comparison of predicted optical rotations for each stereoisomer. As all 4 isomers bear diastereomeric relationships between each other, they would be expected to have different optical rotations, allowing differentiation between stereoisomers.
References
- ↑ N. L. Allinger, J. Am. Chem. Soc., 1977, 99, 8127-8134, DOI:10.1021/ja00467a001 .
- ↑ N. L. Allinger, Y. H. Yuh, and J.-H. Lii, J. Am. Chem. Soc., 1989, 111 8551-8565, DOI:10.1021/ja00205a001 .
- ↑ N. L. Allinger, K. Chen, and J.-H. Lii, J. Comput. Chem., 1996, 17, 642-668, DOI:http://dx.doi.org/10.1002/(SICI)1096-987X(199604)17:5/6<642::AID-JCC6>3.0.CO;2-U.
- ↑ S. J. Weiner, P. A. Kollman, D. A. Case, U. C. Singh, C. Chio, G. Alagona, S. Profeta, and P. Weiner, J. Am. Chem. Soc., 1984, 106, 765-784, DOI:10.1021/ja00315a051 .
- ↑ R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus, J. Comput. Chem., 1983, 4, 187-217, DOI:10.1002/jcc.540040211 .
- ↑ W. Damm, J. Tirado-Rives, and W. L. Jorgensen, J. Am. Chem. Soc., 1996, 118, 11225-11236, DOI:10.1021/ja9621760
- ↑ 7.0 7.1 J. P. Clayden, N. Greeves, S. Warren and P. D. Wothers, Organic Chemistry, Oxford University Press, Oxford, 2001, ch. 35, pp. 912.
- ↑ P. Crabbé, in Topics in Stereochemistry, ed. N. L. Allinger and E. L. Eliel, Wiley-Interscience, New York, 1974, vol. 1, p. 112
- ↑ L. A. Paquette, N. A. Pegg, D. Toops, G. D. Maynard and R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283.
- ↑ L. A. Paquette, Angew. Chem. Int. Ed., 1990, 29, 609-626.
- ↑ 11.0 11.1 W. F. Maier, and P. v. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891-1900, DOI:10.1021/ja00398a003
- ↑ J. E. McMurry, and C. N. Hodge, J. Am. Chem. Soc., 1984, 106, 6450-6451, DOI:10.1021/ja00333a074
- ↑ 13.0 13.1 A. B. McEwen, and P. v. R. Schleyer, J. Am. Chem. Soc., 1986, 108, 3951-3960, DOI:10.1021/ja00274a016
- ↑ B. Halton, and S. G. G. Russell, J. Org. Chem., 1991, 56, 5553-5556, DOI:10.1021/jo00019a015 .
- ↑ 15.0 15.1 B. Halton, R. Boese, and H. S. Rzepa, J. Chem. Soc. Perkin Trans. 2, 1992, 447-448, DOI:10.1039/P29920000447
- ↑ J. Y. Cha, J. T. S. Yeoman, and S. E. Reisman, J. Am. Chem. Soc., 2011, 133, 14964-14967, DOI:10.1021/ja2073356 .