Rep:Mod1:yz908

Introduction of Molecular Mechanics (MM) Modelling

Introduction

Chemical reaction is a transformation process that's taking place in order to change one substance to another. The conditions can be energy demanding, spontaneous, non-spontaneous, etc. Normally, some forms of energy source are needed in order to initiate the reaction by providing sufficience energy to overcome the barrier, such as those used for breaking and forming chemical bonds.

Chemical reactivity is the ability of a substance to undergo certain chemical reaction bearing a change of product. It reflects how fast, how efficient a certain reaction is. This parameter of a reaction often represents relative chemical properties, and is bearing a lot information about the specific starting materials. For example, different chemical processes are applied in synthetic routes in order to produce a desired product. In biochemical processes, enzymes are used in order to catalyse the reaction by lowering the energy barrier. This then increases the rate, at which the reaction goes to obtain a better performance. Therefore, the concept of equilibrium constant is introduced in order to have a better view of what's happening in a system.

In recent years, huge amount of money was spent on researches of various optimaisation of reactions. Both biologists and chemists are focusing on discovering new molecules and potential catalysts to speed up the reactions. Useful techniques to study the geometry of molecules in order to predict the products in certain chemical reacitons are widely analysed. Here, the Molecular Mechanics method is investigated and understood by analysing the structure of products and predicting the potential mechanism. This method is of wide use, and well understood and easy to apply. Models generated from this approach have been very successful in study chemical reactions.

In this study, the main aim is to optimise the total energy of structure and conformation of molecules in order to understand the relative reaction mechanisms.

Method used: Molecular Mechanics

Molecular Mechanics Calculation is introduced here. It is used to study the motion of molecules and nucleus by using classical physics predictions. Therefore the total energy of a certain geometry is calculated in a well settled force field. Energy is obtained in the following way: E = E_bond + E_angle + E_dihedral + E_{electrostatic} + E _{van der Waals}

To understand the 3D effects on chemical reactivity, various techniques can be used as essential tools. The traditional plastic models are widely applied in order to study the structures, strain, and steric hindrance effects, etc. However, there are certain physical limitations associated with these models. To solve the problem, theory tells us that Schrodinger Equation is a better way to calculate all the properties related to the molecule to a greater extend of accuracy. Now, another issue is raised when using this method, regarding errors. The source might come from computer calculation, length of running time, and other summation factors. Therefore, one has found a more effective method by using Molecular mechanics (MM) to summarize all the bond properties and then drives a better approach to solve the problem without the need of Schrodinger calculations. It is then possible to obtain an minimum energy by adjusting the molecular geometry to a optimised conformation with the best suitable bond angles. From the calculation, one can then analyse the bond properties, angles and dipole/dipole values for a much more stable structure.

In this experiment of Module 1, MM2 force field is used by ChemBioDraw Ultra 12.0 to perform the optimisation of energy for a better molecular geometry. Hence, the best conformation of molecule is determined and analysed accordingly.

The results of MM2 force field are summarized as follows: 1) value of diatomic bond stretches. 2) value of tri-atomic bond angle. 3) value of tetra-atomic bond torsions. 4) value of non-bonding Van der Waals' interactions (mainly repulsions). 5) value of electrostatic attractions of individual bond dipoles.

These calculations are very easy and simple to execute using the appropriate programme, computationally available. Therefore, the final total energy (in kJ/mol) is obtained by a summation of all these factors. However, MM2 force field is suitable for small molecule calculations. It works maximum on simple hydrocarbon chains with less bulky substituents.

Hydrogenation of Cyclopentadiene Dimer

Dimerisation of Cyclopentadiene

Cyclopentadiene has molecular formula C5H6. It has a uncomfortable odor and often appears as a colourless liquid. Normally, cyclopentadiene dimerizes in air at room temperature and pressure. This results in the formation of dicyclopentadiene undergoing a Diels-Alder reaction. The process is reversible. However, if treated under heat, the dimer will soon break into its original monomers. Under low temperature conditions (generally approx -20°C), the monomer could be stored for several days if no other reactions.

Cyclopentadiene dimerizes through a [_π4+_π2] cycloaddition reaction. This reaction then gives 2 different products, which are stereoisomers of each other. There are either endo- or exo- as indicated below:

Exo-dicyclopentadiene

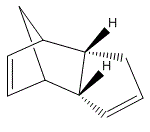Endo-dicyclopentadiene The dimerization proceeds via a concerted reaction, results in stereospecific products with dienophile. The reaction is also said to be stereoselective with respect to the relative position of the unsaturated C=C double bond to the diene. Exo-dicyclopentadiene: The Functional group or subsitutent is furthest from the 'original diene'. Endo-dicyclopentadiene: The Functional group or subsitutent is closest to the 'original diene'. Attractively, one of these stereoisomers is treated as a thermodynamic product, another as a more kinetic product. In the molecule of dicyclopentadiene, the 'original diene' is now the C=C on the left hand side of both molecules. Diels-Alder reaction is commonly found to give rise to two stereisomeric products. This is due to the fact that the reaction proceeds to form bicyclic or tricyclic compounds.

Upon calculations using ChemBioDraw Ultra 12.0, the results are summarized in Table 1 below:

Properties	Exo-dicyclopentadiene	Endo-dicyclopentadiene	Difference
Stretch	1.2829	1.2454	0.0375
Bend	20.6136	20.8603	-0.2467
Stretch-Bend	-0.8320	-0.835	0.003
Torsion	7.63302	9.5039	-1.8709
Non-1,4 VDW	-1.42138	-1.5083	0.08692
1,4 VDW	4.2377	4.3012	-0.0635
Dipole/Dipole	0.3770	0.4448	-0.0678
Total Energy (kcal/mol)	31.8915	34.0153	-2.1238

Table 1: Relative Energies in kcalmol^-1 for comparison

The thermodynamic product is the lowest energy product, whereas the kinetic product is the most easily obtained product. The thermodynamic product was found by calculating total energies of geometrically optimized final product confirmations. According to Table 1, it is seen that the total energy of Endo product is 2.1238 kcalmol^-1 higher than the Exo product, which shows that the Exo product is actually more thermodynamically stable. The biggest difference arises from the torsion strain, in which the Exo product is 1.8709 kcalmol^-1 more stable. This is attributed to the difference in torsional strain around the new C-C bond formed. The Endo product gives a 47° dihedral angle, corresponding to a gauche conformation around the new C-C. However, the Exo product gives a 168° angle, indicating an antiperiplanar conformation and appears less satirically bulky. Hence, the electrostatic repulsion between the π-electrons is minimized. This steric strain explans the reason why Exo isomer is more stable in energy term.

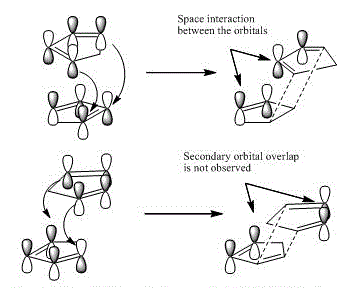
In the diagram above, the orbital interactions can be clearly seen at the transition states of the reaction process. Top case represents the endo- product, and the bottom case is therefore for exo- product. The stabilization of transition state comes from the fact that when the π-bond, and its p-orbitals approach the newly formed C-C bond, which also have π-electrons on it. The condition, in which the kinetic product is prefered, is when the energy of the reaction is not sufficient to overcome the high activation barrier, so the kinetic product forms at a best suitable transition state with smaller activation energy. On the other hand, when the energy of the reaction is high enough for all molecules to overcome the energy barrier, thermodynamic Exo-product will formed. The kinetic product can therefore be identified by comparing transition energies of the two optimized transition geometries. With further calculation, the Endo product has a lower energy of -75.976632697 Hartee, Exo of -75.9746926771 Hartee. The difference in transition energy is then calculated and converted to be 1.217 kJ. The following equation ΔΔG=-RTlnΔk is used to calculate the difference in rate constants. It is then found that the rate of Endo-product formation is much faster than the Exo-product formation. Therefore Endo product is obtained as kinetic product under normal temperature and conditions.

Now, one can summarize that cyclopentadiene dimerises to produce Endo Dimer rather than the Exo Dimer at room temperature and normal pressure.

Hydrogenation of Cyclopentadiene Dimer

Hydrogenation of Cyclopentadiene Dimer to tetrahydrodicyclopentadiene over catalyst is undergoing the reaction shown below. The reaction is a consecutive process with two types of intermediates. This experiment has confirmed the double bond in the 6-membered ring is easier to hydrogenate than that in the 5-membered ring, so the major intermediate is called 8,9-dihydrodicyclopentadiene (8,9-DHDCPD). The reaction proceed at lower temperature. The reaction conditions include temperature and hydrogen pressure being optimized.

Exo-dicyclopentadiene

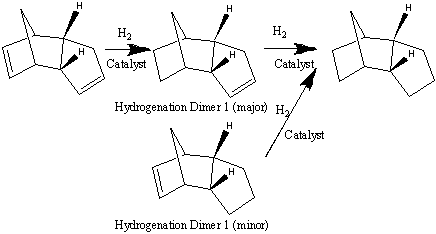
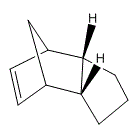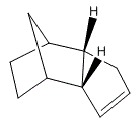Endo-dicyclopentadiene The total energies of the two hydrogenation product are compared to obtain a more thermodynamic prediction of pathway the reaction is under taking. According to the calculation from MM2, Hydrogenation Dimer 1 gives a total energy of 35.9307 kcalmol-1, which is less stable than the Hydrogenation Dimer 2, which gives a total energy of 31.1911 kcalmol-1. The Calculation is a summation of all the other factors, stretch, bending, torsion and interaction energy are combined to generate this optimized value. Therefore, the MM2 calculations show that Hydrogenation Dimer 2 is the thermodynamically more stable product with a total energy 4.7396 Jmol-1 lower than Hydrogenation Dimer 1. It is obvious that the main contribution to this difference is the bending energy.

Upon calculations using ChemBioDraw Ultra 12.0, the results are summarized in Table 2 below:

Properties	Hydrogenation Dimer 1	Hydrogenation Dimer 2	Difference
Stretch	1.235	1.1020	0.133
Bend	18.9652	14.5211	4.4441
Stretch-Bend	-0.7602	-0.5462	-0.214
Torsion	12.1494	12.5199	-0.3705
Non-1,4 VDW	-1.5548	-1.0414	-0.5134
1,4 VDW	5.7330	4.4950	1.238
Dipole/Dipole	0.1632	0.1409	0.0223
Total Energy (kcal/mol)	35.9307	31.1911	4.7396

Table 2: Relative Energies in kcalmol^-1 for comparison

According to the table above, the significant difference between the energy for Hydrogenation Dimer 1 and 2 include the bending and torsional energy. Hydrogenation Dimer 1 has a much higher bend energy, which can be attributed to the larger angle strain experienced by the C=C double bond in the 6-membered ring. The bond angle is slightly different from the optimal angle of 120°. However, upon hydrogenation of the C=C bond in 6-membered ring, the angle now becomes 110°, which is much closer to the optimal angle of 109°. For torsional angle, Hydrogenation Dimer 2 has a larger dihedral angle of around 0.39°, which is much larger compared to Dimer 1 0.02° and much favourable. In conclusion, the C=C double bond is long and therefore weaked, easier to break. All these terms calculated attribute to the fact of Hydrogenation Dimer 2 with 6-membered ring being hydrogenated, being more stable.

The experimental data has shown an very good agreement with the theory and actual observations. Hydrogenation of the Cyclopentadiene Dimer happens via two intermediates. However, when treated with prolonged hydrogenation is the tetrahydrogenated product formed, which is shown below:

Tetrahydrogenated Dimer Properties Tetrahydrogenated Dimer Stretch 1.1155 Bend 12.9776 Stretch-Bend -0.4828 Torsion 16.9124 Non-1,4 VDW -1.3354 1,4 VDW 6.0969 Total Energy (kcal/mol) 35.2842 Table 3: Energy for Tetrahydrogenated Dimer. From comparison of the energy of the tetrahydrogenated product with Hydrogenation Dimer 1 and 2, the total energy of the tetrahydrogenation product is slight higher. Hence, the tetrahydrogenated product is less stable. The main factor here is the torsional strain. The dipole/ dipole contribution for the tetrahydrogenated product also increased more than the previous hydrogenations, which gives rise to Hydrigenation Dimer 1 and 2. In general, this process of tetrahydrogenation is not particularly thermodynamically preferred. Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ analogue)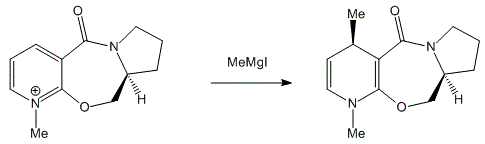 The N-methyl salt of pyridinium ring undergoes regio- and stereoselective addition with Grignard reagents methyl magnesium iodide (MeMgI) to give an selective product. Selectivities can be as high as more than 90% according to observations. The nucleophilic addition of Grignard reagents to N-methyl salt is both highly regio selective and stereo selective. When the methyl magnesium iodide (MeMgI) is attacking N-methyl pyridoxazepinone, it is suggested that the Mg atom, which is electropositive, binds onto the electronegative oxygen atom on the carbonyl group. The adduct is shown on the left. This would then allow the Methyl group to be added nucleophilically from the top phase of the molecule in order to obtain the stereoselective and regioselective product. A combination of different conformation energies of the N-methyl pyridoxazepinone (starting material 5 as suggested in the instruction wiki) was calculated using MM2 to obtain the best suitable and energetically favoured conformation. The result represents an equilibrium position and uniform conformation for the molecule. This finding is key to show the mechanistic process with the Grignard reagent MeMgI. The critical point here is to decide the relative position of C=O bond in the 7-membered ring structure on the right hand side of the molecule compared to the N-methyl ring in the aromatic 6-membered ring. The decision made from this calculation will ultimately determine the conformational outcome. From MM2 calculations by changing the optimal dihedral angle, the conformation of N-methyl pyridoxazepinone with lowest total energy was decided with a minimum of 37.6743 kcal/mol (around 157 kJ/mol). This is ptimised according to the analysis on dihedral angles between the amide carbonyl C=O bond and the neighbouring C4 C-H bond in the pyridinium ring. The graph on the left showns the relationship between the total energies against the dihedral angles. The optimised minimum appears at the position where dihedral angle is around 23.8 degrees, with C=O bond being above the plane of the neighbouring aromatic ring. 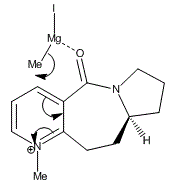Hence, this conformation analysis and the graph can clearly show the reason behind the nucleophilic attack by the Grignard reagent MeMgI. The regio and stereo selectivity are now obvious in confirming the attack from above the plane of the molecule. It is also shown the absence of a conformation with C=O abelow the pyridinium ring. Because of the 23.8 degrees in dihedral angle, electropositive Mg can therefore bind to the oxygen atom from the top face. This process is calculated to be very much favoured in term of total energy of the structure. Jmol of the lowest energy N-methyl pyridoxazepinone Reaction of Quinolinium Salt with Aniline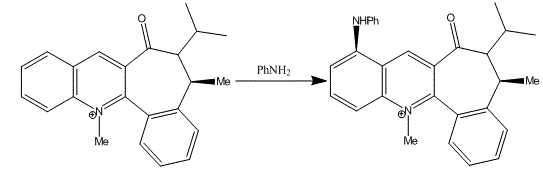 The reaction of Quinolinium Salt (Molecule 7 shown in the instruction wiki) with aniline has studied and the best conformation is analysed with MM2 calculations. Similarly, it is found that the nucleophilic addition of aniline to N-methyl quinolinium ring is also stereo and regioselective. An Energy Analysis of different conformations is studied by changing the optimal dihedral angle of the C=O bond with respect to the N-methyl quinolinium ring. The graph was plotted in order to determine the best conformation. Mechanistically, the aniline molecule attack nucleophilically by the lone pair of electrons on the nitrogrn atom to the N-methyl aromatic ring. Similar to the previous example, the geometry of N-methyl quinolinium was optimised by the dihedral angle, which shows a energy minumum at -20o, with the negative sign indicating C=O bond in the 7-membered ring staying below the plane of the molecule. Due to the presence of C=O being underneath the plane of the ring, when alinine molecule is attacking nucleophilically. The bottom face is very much sterically hindered and less energetically favourable. This is hence the reason why the newly added substituent appears at the top face of the N-Methyl aromatic ring on the left hand side of the molecule. Different from the previous Grignard reagent reaction, aniline molecule does not have such electropositive atom, for example: Mg. Therefore, the chelating effect observed before between the amide O atom and the nucleophile is not the case here. The transition state is not happening. Alternatively, this reaction proceeds via lone pair attack on the electrophilic C4 carbon in the neighbouring pydinium ring. This is the reason Leleu et al. has shown that the process is extremely stereo- and regioselective, with high yield of above 90%. 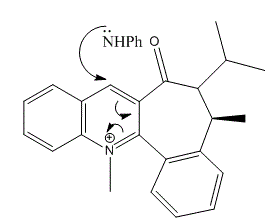Jmol of the lowest energy N-methyl Quinolinium Salt Potential Improvements on the MM2 Method From this experiment, it is obvious to agree that the MM2 method from ChemBio3D office is a useful way in optimising the structures resulting in stero- or regioselective products. It helps to obtain the best suitable geometry for nucleophilic reactions. The MM2 method uses a force field in applying eauqtion for minimal energy calculations. Due to this applied force field, not all the molecules with various conformation and characteristics are able to be calculated correctly. The calculations are based on the fact of nuclei interactions without the effect of any electron interactions. It is however the electons that act as importment players in these reactions involving bond making or breaking. Althought Molecular Mechanics is effective in finding the most stable conformation of a structure, there are potential improvements, which can be done. One way is to use Density Function Method, which applies the law of quantum mechanics to perform the calculation, and then solving the Schrodinger Equation. Alternatively, in order to improve the MM2 method, a better and more detailed force field could possibly be applied, or more potentially applicable parameters in the calculation. By including the electronic interaction might also be a good approach to potentially improve the solutions.The concept of orbital calculations, relative energies of HOMO and LUMO energy levels can also be studied and included for better optimisation of energies and geometries. Additionally, Gaussian Calculation could be used to minimise the energy of structures and obtain the best geometries. Another way is to add bulky substituent in order to make the molecule more rigid and less conformationally easy to handle. As a result, the regioselectivity and stereoselectivity of the reaction taking place will be improved. This is due to the large energy barrier raised by making molecules less flexible. Although in this method, the minimal energy might be increased by a small amount, the accuracy would be possibly improved. Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol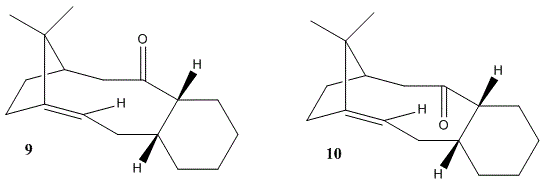 Taxol, called Paclitaxel in medicine, is a drug used in cancer treatment. Paclitaxel is normally used in cancer chemotherapy, and is therefore an anti-cancer drug. It has been around for many years now to be applied in generic formulation. Taxol is a white powder and processed to obtain a colorless liquid to treat the following cancers: such as Ovarian Testis, Breast Cancer, Head and neck cancer and Lung cancer. It is also used in conjuction with other drugs such as: Cytoxan and Cisplatinum, etc. In order to synthesize Taxol, it has been proved that the intermediates are atropisomers of each other. Atropisomerism shows stereoisomers due to the restricted rotation about hindered single bonds, in which the energy barrier to rotate is too high. This is therefore the reason why the isomers are able to be isolated for further analysis. The intermediates during the synthesis process are shown above as Molecule 9 and 10. Measurement C=O group pointing up C=O group pointing down Stretch 2.8309 2.7755 Bend 16.4731 12.2500 Stretch-Bend 0.4582 0.3648 Torsion 21.3974 22.6340 Non-1,4 VDW -0.9453 -0.7518 1,4 VDW 14.0500 13.7404 Dipole/Dipole 0.1365 -0.1906 Total Energy (kcal/mol) 54.4008 50.8223 Molecule 9: C=O group pointing up Molecule 10: C=O group pointing down Molecule 9 Molecule 10 In the synthesis of Taxol molecuel, the reaction undergoes via two intermediate either Molecule 9 or Molecule 10, with total energy of 227.76192 kJ/mol and 212.68944 kJ/mol respectively. In the first intermediate, the C=O bond is pointing upwards, and the second molecule has C=O bond pointing downwards. Another aspect, which is able to improve is the adjustment of the 6-membered ring, to make sure it has a chair shape instead of boat. The dihedral angle of the C=O bond is also optimised compared to the the 6-membered ring for both molecules. Although MM2 Calculation is able to optimise the energy of a molecular structure, there is still space to improve the method and use other principle in obtaining the optimum geometry. The starting material for the synthetic process can also be analysed in order to compare with the intermediate energies. By comparing the bending contribution to the difference in total energy, Molecule 9 has obviously higher strain than Molecule 10. This attributes to the higher total energy for this geometry. This is due to the cyclohexane ring is being sterically hindered and strained in a twist-boat conformation, C=O group in this case is pointing up in the molecule. However, in the intermediate molecule 10, the low energy happens due to C=O bond pointing below the plane, and the molecule takes a chair conformation. This is a much more stable geometry of structure. C=O carbonyl groups are very reactive in Chemistry, which occurs rapidly. Bearing the group inside the target molecule, it is therefore essentially to obtain an optimised geometry. In this experiment, MM2 methods and MM9 are used to determine the most suitable shape. This analysis hence shows that upon MM2 calculation, one is then easy to define the outcome of the reaction to obtain the product from intermediate molecule 10. Reactivity of Olefin functionality in the intermediates Olefins are recognised and identified by using the measurements of olefinic strain energy (OS). It indicates the relative strain behind the C=C double bond compared to the saturated chain. Olefin Strain Energy can be obtained by removing the strain energy from the alkene, and is driven by heating. In order to determine the activity of the reaction, Olefin Strain Energy (OSE) needs to be calculated. Olefin Strain Energy is the difference in energy between the olefin and the original hydrocarbon chain. Hyperstable alkenes are very stable commpared to straight hydrocarbon chains. Normally, the olefin is more hindered and hence geometrically strained than the single straight chain of alkene. Alkene is generally positive in olefin strain energy. This reflects itself to be capable of undergoing certain reactions. Some literatures have shown that certain olefin shows negative olefin strain energy, and more strained than the original hydrocarbon, the reactivity of the olefin is hence reduced . When different isomeric molecules are available for a particular reaction, the olefin will be discovered at the bridgehead positon, which are thought to be more thermodynamically stable. The lowering in energy is considered to be the increase in steric builk hence increase group repulsion between bridgehead and olefin functionality, decrease in rate of reaction. π-bond strength can also be increased. Prediction and conclusion It has been proved that the stability is at the bridgehead olefin. Therefore, the olefin strain energy is of a negative value, and found to be decreasing in reactivity in terms of comparing to C=C double bond. Due to this strain, the alkene functional group C=C in olefin reacts less rapidly compared to the hydrogenation. These alkenes are identified to be hyperstable. Hyperstable Olefins has therefore been defined as alkenes, that are more sterically strained, hence less reactive. Hyperstable olefins are identified by negative OS energies. In conclusion, hyperstable olefins are extremely important in synthesis processes, including reduction routes. Modelling Using Semi-Empirical Molecular Orbital Theory Short Introduction Molecular Mechanics is a very useful method in optimising energies. It has its strengths and also weaknesses. Due to the limitations associated with this calculations, it does not include the secondary orbital factors in discussing the examples, such as endo stereoselectivity in Diels Alder cycloadditions. Due to the only nucleus interations, an alternative method is used to take into account of the electronic contributions of the molecule, in which it is well analysed in the Semi-Empirical Molecular Orbital Theory. Semi-Empirical Molecular Orbital Theory is a better tool in modelling the target molecule in its best suitable geometry, this is well analysed compared to the previous method using MM2 calculations. As the title of Molecular Orbital implies, this approach optimises the geometry by considering the general shape of molecular orbitals, contains only the Semi-Emperical forms and energy terms. The best energy is also obtained by applying a field, in which all the calculations are taking place. It contains the ways of identifying the right atomic and molecular orbitals. As we all know, chemical reactions often happen in the HOMO-LUMO energy levels, because this is the region that the valence electrons are normally found and controlling the chemistry by bond formation and breaking. Therefore, HOMO-LUMO molecular orbitals are crucial in defining the chemistry. In this experiment, the aim is to learn to use computational models in building up HOMO-LUMO molecular structures. From analysing the shape and energy of such orbitals, the reactivity and reletive regio- and stereo-chemistry are studied. In this case, MM2 calculations and PM6 methods are both used in the calculation processes. It is obvious that the MM2 stimulation does not involve the electronic interaction into energy optimisation, however, is it efficient in obtaining the best geometry for the target molecule first. After the success in finding the structure, PM6 method is used to apply the Molecular Orbital theory in studying the electron cloud and orbital effects for energy understanding and optimisation. Procedures Part 1: Orbital contribution in defining reactivity is discussed here with molecule 12. The reagent is taken to react with chlorocarbene or peracid. We model the molecule according to their relative orbital interactions. In this experiment, quantum mechanical technique is applied in order to substitute the original classical physical in producing wavefunction to analyse the electronic effects. This is done by first using ChemBio3D to perform the MM2 calculation in and obtain the best geometry of the molecule. The MOPAC/PM6 or MOPAC/RM1 MO can be successful in representing valence-electron molecular wavefunction, hence susceptable to electrophilic attack. Part 2: The interaction of Cl-C bond with the vibrational frequencies of the whole structure is calculated. Molecule 12, in which the C=C bond is antiperiplanar to Cl-C bond is compared with the hydrogenated one, in which the antiperiplanar C=C bond is reduced to C-C single bond. For this process, MM2 is used first to obtain the best geometry of the molecule and then Gaussian geometry optimization and frequency calculation is performed. Part 3 Substituents are modified on the antiperiplanar C=C double bond. Electronic effect on the Cl-C and C=C frequencies is analysed. Molecular Orbital controlled reactions It is a better way to model molecules using Semi-Empirical Molecular Orbital theory. This method uses empirical forms and calculated the energies of the molecular orbitals in order to give the best suitable geometry. The optimisation is performed using self-consistent field. The method does not involve the differential overlap, nor the diatomic differental overlap. In this experiment, the reaction of Molecule 12 with electrophile dichlorocarbene and peracid showns the demonstration of orbital interactions. The whole process is seen as an electrophilic addition. Starting with molecule 12, the dichlorocarbene reagent is added in, a cyclic product is produced. This is driven by the movement of electrons in between the molecules. MM2 calculation is used first to obtain a best conformation for molecule 12. The total energy is calculated out as 17.9126kcal/mol from ChemBio3D. Molecule 122 During a certain reaction, the chemistry often happens at the HOMO-LUMO energy levels, in which the valence electrons are active. This is the the reason why normally the chemical reactivity is defined by the electrons and orbital characteristics in the HOMO-LUMO levels. In this experiment, the HOMO-LUMO orbitals are computed and explained here, the regioselectivity of the addition reaction is then defined. MM2 does not include any electronic effects in its calculation when obtaining the geometry optimisation. PM6 method was then applied, in which the electron wavefunction is analysed during the optimisation process to produce the orbitals. Molecule 12 has a structure shown above, which contains two C=C bond and they are susceptible towards electrophilic attack. Since there are two potential attacking points, the orbital interaction and other steric effects have to be taken into account. It is identified that the attack will normally happen 'syn' to the Cl atom (C=C closest to Cl-). This is due to the steric hindrance and also the stabilisation created between C-Cl σ*-orbital and pi-orbitals from the C=C bond. When dichlorocarbene is attacking the C=C of Molecule 12, endo product will form.. The Reaction Scheme and the HOMO-LUMO orbitals are shown below: 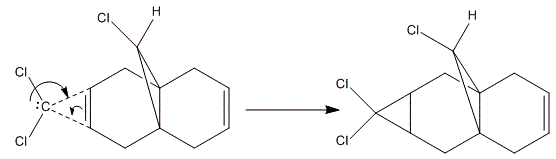LUMO +2 LUMO +1 LUMO HOMO HUMO -1 Orbital Analysis From the Orbital Analysis table, it is shown that a high electron density around syn C=C bond position in both HOMO and HOMO-1. This is why the 'syn' position is more nucleophilc compared to the 'anti' C=C position. This is the reason that 'syn' C=C is a better nucleophile and is better at electrophilic addition reaction. By looking at HOMO-1 and LUMO+1 orbitals, they are similar in shape and geometry. Therefore, they are app to both the C-Cl σ* orbital and HOMO-1. Due to the stabilisation energy of those orbital, the anti C=C, exo π-orbital of C=C is less stabilized and is not that likely to be able to get electrophilic attack. It is also suggested that HOMO and LUMO +1 have overlap due to similar shape and geometry. However, Halton et al have proved that if this is the case, the orbital energy will be 0.08eV higher than the one with HOMO-1 and LUMO. In general, the HOMO-1 orbital is the most stabilised one and the syn C=C bond is more likely to get attacked by nucleophile in the electrophilic addition. The MM2 calculation gives a optimisation shape of Molecule 12, in which the distance of exo C=C bond and the central bridgehead C-C bond are shorter than the endo C=C distance. This is due to the stabilisation from C-Cl o*-orital of LUMO+1 and exo C=C pi-orbital of HOMO-1. The pi-orbital donate electron density into the antibonding C-Cl o*-orital weakening the carbon to chlorine single bond. This is also a reaction for endo C=C bond being attacked by electrophiles showing its regioselectivity of this reaction. Infrared Analysis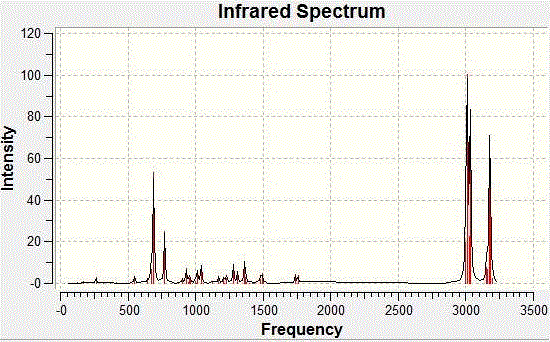 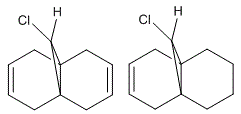Now, when the molecule 12 is hydrogenated, the exo C=C bond is changed into C-C single bond. To analyse the bonds, Vibrational frequencies of Cl-C and C=C and C-C bonds are obtained from IR spectra (shown above). The relative IR peaks and intensities are tabulated below for comparison. Bond Type IR peaks/cm-1 Intensity C-Cl 772.80 25.23 endo C=C 1758.11 3.68 exo C=C 1739.01 4.32 Bond Type IR peaks/cm-1 Intensity C-Cl 775.94 20.21 Syn C=C 1758.61 - Upon hydrogenation, the exo C=C bond is changed into C-C single bond, hence the exo pi-orbital and C-Cl o*-orbital interaction disappears. Therefore, less electron density is donated into the antibonding C-Cl orbital, bond order is higher, bonds stronger, and shorter. That's the reason why higher vibrational frequency shown for C-Cl in going from Molecule 12 IR (Table on the left) to Hydrogenated Molecule IR (Table on the right). The clear increase of the C-Cl bond length, when exo C=C bond is hydrogenated, is shown as about 3cm-1 in IR spectrum. The exo bond strength is about 18cm-1 weaker than the endo C=C bond. This can be explained by the fact of electron densitry being donated from C=C pi-orbital into the C-Cl antibonding orbital, which destabilises the C-Cl bond. After hydrogenation, the effect is not seen. Due to the only endo C=C bond existance, there is only one C=C IR frequency in the spectrum. The C-Cl bond is stronger, shown with higher IR frequency. Literature for IR frequency of C-Cl bond is at 740-780 cm-1 This has indicated that the results obtained from computational methods are ina a good agreement with the experimental values. This is also verified by showing the C=C bond frequencies similar to literature of 1630-1680 cm-1 However, the computational IR are around 1758.61 and 1758.11 cm-1, which is a little higher than normal. This attributes to the app position, which is high stabilising. Molecular Orbital Modelling Summary This experiment has clearly shown a success in using the Semi-Empirical Molecular Orbital theory to determine the optimised geometry of structures. In this metrod, the electronic interaction has been included in the optimisation process as well as the enery calculation. Structure Based Mini Project using DFT-based Molecular Orbital Methods Introduction Azetidinones are commonly known as β-lactams. The β-lactams are often used as synthons for many biologically organic molecules. This is partly the reason that the chemistry and biology of these substances continue to appeal in synthetic and medicinal fields. They are heterocyclic organic compounds, which are of great uses among the organic and medicinal industry. Azetidinone has a four membered ring structure at the centre of the molecule, with nitrogen atom at one of the vertices of the ring. The presence of the Azetidinone ring, in a lot of well-known antibiotics such as penicillins,cephalosporins and carbapenems, has great control over the activity and functions of those molecules. The large importance and geometrically diversity of the biologically active β-lactam antibiotics has contributed hughly to the development of Azetidinone synthesis with various functional group control and stereochemsitry. In recent years, other kinds of biological activities have been discovered in subtances containing Azetidinone ring. These activities include antifungal, antitubercular, cholesterol absorption inhibition and other enzyme inhibition activity. All these functionalities could be used as essential means for the protein characterisation, and cholestetol control in the human body. One of the means to synthesise Azetidinone is shown as follows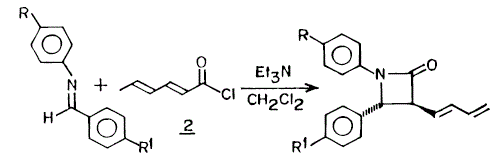: Another method to synthesise Azetidinones is the Staudinger keteneimine cycloaddition, which contains imines reacting with acid chloride in conditions with tertiary base. The conditions are usually highly sensitive to temperature, and some other external factors. The Azetidinones synthesised from imines of thiophene-2-carbaldehyde and diarylketenes, have also showed antibacterial and antifungal ability. The investigation of new directions into synthesis of β-lactams has been a centre of research on possible uses as biologically active molecules or as chiral structures. MM2 Optimisation of the Mini Project Azetidinones are useful reagents, which could be used with various nucleophiles in different reactions. In this experiment, Azetidinone was taken to react with maleic anhydride in order to undergo a [4π + 2π] Diels-Alder cycloaddition reaction. Toluene is chosen as the solvent. The reaction mechanism is shown below: The proposed mechanism for the reaction betweem Azetidinone with maleic anhydride is shown as follows: 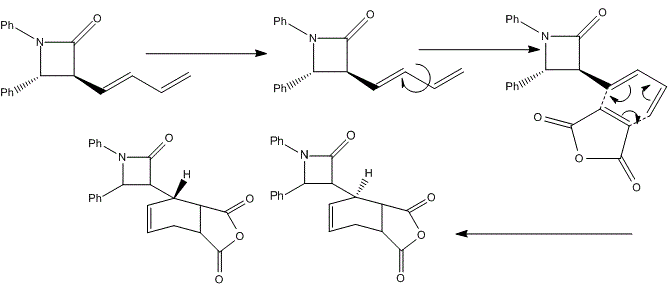During the discovery of Azadieneketene cycloadditions, it has been found that the use of butadinenylketene in this cycloadditions is a efficient synthetic route. It has been discovered that during the reaciton process, there are two different stereoisomers produced after reaction. Sharma et al has shown that the reaction of the Azetidinone with DMAD and PTAD resulted in diastereoselective synthesis of the corresponding Diels−Alder adducts. However, the reactions with MA and NPM yielded a mixture 2:1 of diastereoisomers. Therefore, the product mixture (shown above in the reaction scheme) has a weighting ratio of 2:1. This indicates that the product isomer with the hydrogen pointing 'up' will have the lowest energy, hence being produced with the most stable geometry. This result has then been analysed using computational methods to prove the finding. MM2 calculation is first used to minimise the total confirmation energy. The orbital interaction together with IR and NMR analysis are done for comparison with the literature values. The two products, which are stereoisomers of each other are shown below: H-pointing up H-pointing down H-pointing up H-pointing down Measurement Hydrogen pointing up Hydrogen pointing down Stretch 2.2394 2.1367 Bend 31.0745 24.1294 Stretch-Bend -0.6824 -0.7556 Torsion 10.5085 11.8821 Non-1,4 VDW -6.9839 -7.8900 1,4 VDW 19.9694 19.9255 Dipole/Dipole 3.3249 3.2763 Total Energy (kcal/mol) 59.4504 52.7044 According to literature, the -Ph group on the nitrogen is pointing inside the plane of the molecule. Hence, it is proved that the hydrogen atom as pointed in the reaction scheme (with either bonds pointing into the plane or pointing outside of the plane) is identified as having lower energy when pointing down into the plane of the molecule. This conformation is much more stable due to the reduced sterica hindrince effect with the big bulky group of maleic anhydride substituent. From MM2 calculation, the results have shown a good agreement with the theory. In the case of hydrogen atom pointing down (inside the plane of the screen), the total energy is seen to be much lower than when the hydrogen atom is pointing up (outside of the plane of the screen). The main contribution to the total energy of the molecule when hydrogen is pointing up is the bending energy, which arises from the strain of the builky phenyl groups. This difference in energy calculation shows then fact that the molecule is trying to reduce the steric hindrance between the neighouring phenyl group to have direct effects on each other. Hence, the MM2 optimisation is a useful tool to determine the most stable conformation of the molecule. 13C NMR Analysis of the two Diastereoisomers NMR for molecule with hydrogen pointing up: DOI:10042/to-7369 NMR for molecule with hydrogen pointing down: DOI:10042/to-7370 The molecule geometry is first optimised by following the instructions online. However, the only difference is that the maxcycle was corrected to 40 instead of 25 due to the relative large size of the molecule. This process has been done to increase the accuracy in order to obtain a much more stable conformation. The 13C NMR spectrum can be obtained using DFT technique. The results are shown as follows: The following table shows Computational and Literature Chemical Shift for conformation when hydrogen is pointing up: Arbitary Carbon Number Computational ppm Literature ppm 1 27 24.2 2 37 35.6 3 40.0 40.2 4 43.2 42.7 5 60.3 59.3 6 61.2 60.1 7 119.4 117.0 8 116.8 124.1 9 120.5 124.2 10 123.0 126.1 11 123.9 126.2 12 127.5 128.6 13 126.1 128.8 14 126.1 128.9 15 126.3 129.1 16 127.0 129.4 17 129.0 130.4 18 129.9 130.6 19 135.7 136.7 20 138.6 137.0 21 163.3 165.9 22 170.9 171.1 23 173.0 173.7 According to the NMR analysis, a good agreement has been shown with a matching in computational results and the literature results. This has indicated a successful characterisation through the computational NMR methods. 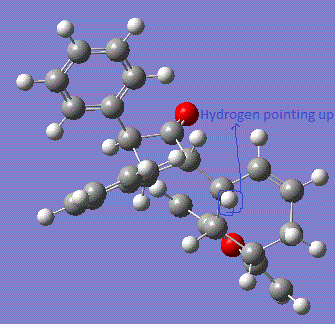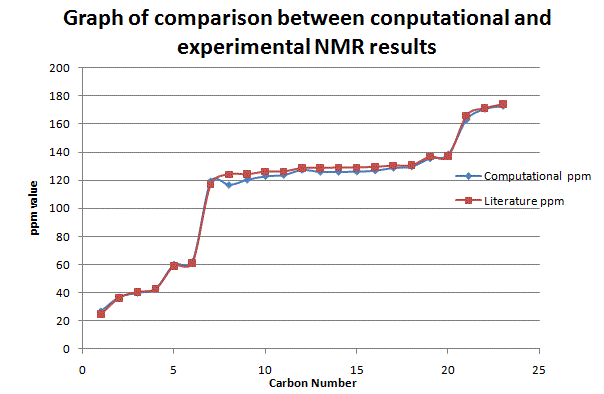The same procedure has been carried out to the other diastereoisomer, and the following table shows Computational and Literature Chemical Shift for conformation when hydrogen is pointing down: 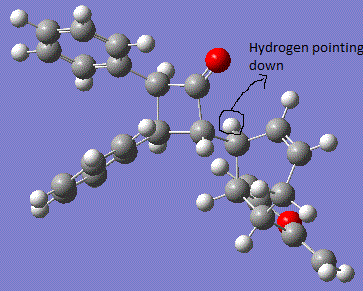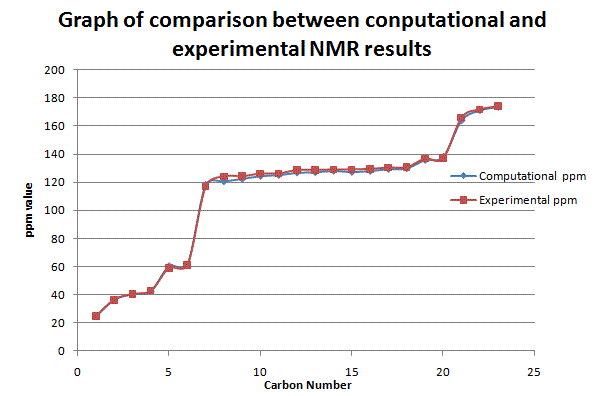Arbitary Carbon Number Computational ppm Literature ppm 1 25 24.7 2 36.9 36.4 3 40.5 40.5 4 42.7 42.9 5 60.7 59.1 6 61.6 61.1 7 118.3 117.0 8 120.7 124.1 9 122.5 124.2 10 124.5 126.1 11 125.2 126.2 12 126.9 128.6 13 127.2 128.8 14 128.2 128.9 15 127.4 129.1 16 128.1 129.4 17 129.5 130.4 18 130.0 130.6 19 135.9 136.7 20 138.3 137.0 21 164.0 165.9 22 171.2 171.7 23 173.6 174 According to the graphical results and computational NMR results, it has seen a clear agreement with the literature values. This shows that the computational mathods are successful in predicting the outcome of the reaction. Both of the diastereoisomers are correctly identified. Although there is a silight difference seen in both graphs between the computational and the literature values, the variation is very small. Further analysis has therefore carried out using Computational Infrared Technique to prove the findings as follows. Infrared Spectroscopy Analysis The computational IR spectra has been obtained in order to further analyse the product stereochemically. The tables below summarises the IR frequencies for stereoisomer with hydrogen pointing up, stereoisomer with hydrogen pointing down respectively. It is noted that the IR frequencies are similar for both conformations, which is due to the similar bonds and stretching in both molecules. However, the difference attributes to the fact that the intensities of peaks are varying. This is due to the change in dipole moment in IR environment. Results are shown below: Bond Type Computational Value/cm-1 Literature Value /cm-1 C=O bond stretch 1810 1771 C=C bond stretch 1711 1738 C=C bond stretch (close to nitrogen) 1553 1594 C=C bond stretch 1492 1496 The frequency range for C=O stretch is around 1660–1800 cm-1. Although the difference between the conputational results and the literature values is quite obvious, it is still within the correct range. All these findings indicate that the computational analysis is a reasonably good way for product prediction. Since Diels-Alder reaction normally react under kinetic conditions and the more kinetically stable product is formed. This computational analysis has given enough evidence in determing the correct product. Conclusion Molecular Modelling is a very effective way to determing the best conformation of molecules, which then allows the correct product being predicted and correct methods being delivered. MM2 Calculation, ChemBio3D and Gaussian are all useful tools of finding the best suitable geometry for certain types of molecules. In these methods, total energy is optimised and hence properties and reactivity of molecules can be predicted. By using computational NMR and IR, the arguments are proved and the molecular findings are hence characterised. This experiment has demonstrated a very efficient metrod to analyse stereochemistry and regiochemistry of various structures. Although this metrod has shown slight deviation from the literature and experimental values, the success in determing the correct geometries by using these methods has shown great uses for future computational chemistry studies. References