Rep:Mod1:yahtingkoh54321

Modelling Using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Dimerisation of Cyclopentadiene

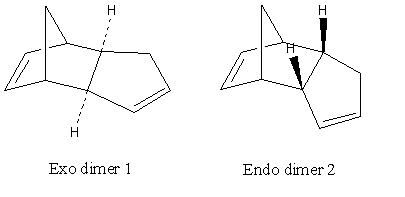
Cyclopentadiene dimerises to produce specifically the endo dimer 2 rather than the exo dimer 1. Using the Chem3D geometry optimisation under MM2, the total energy of the exo dimer 1 is found to be 31.8801kcal/mol, which is lower than that of the endo dimer 2, 34.0147kcal/mol. This shows that the endo dimer 2 is formed, even though it is of a higher product energy. This suggests that this reaction is kinetically controlled, such that the non - thermodynamic product is formed.

The dimerisation of cyclopentadiene is a Diels Alder reaction. It follows that the selection rules by Woodward and Hoffman results in the endo selectivity. Since the Diels-Alder reaction is irreversible, the endo product would be formed irreversibly on kinetic and electronic grounds.

Hydrogenation of Dicyclopentadiene

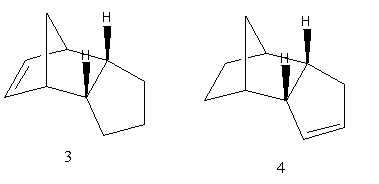
The total energies of the two products of hydrogenation of the endo dimer, products 3 and 4, are also compared. This is tabulated below:

Relative energies	Molecule3	Molecule4
Stretch	1.3040	1.0923
Bend	19.8180	14.5509
Stretch-bend	-0.8382	-0.5475
Torsion	10.8217	12.5014
Non-1,4 Van der Waals	-1.1994	-1.0865
1,4 Van der Waals	5.6307	4.5075
Dipole/dipole	0.1620	0.1406
Total Energy	35.6989	31.1588

The total energy of product 3 is higher than that of product 4. Hence, product 4 would be formed under thermodynamic predictions, and this suggests that the double bond within the cyclohexane ring is more easily hydrogenated than the double bond in the cyclopentane ring. On further analysis of the relative energies contributing to the total energies of 3 and 4, it is observed that the main contribution to the high energy of 3 is the bending energy, which is 5.2671 kcal/mol higher than the bending energy of 4. This high bending energy might be caused by the strain in the bond angles for the C=C bond on 3, 108°, which is smaller than the ideal sp² angle of 120°. Molecule 4 is less strained, with the C=C bond angle being 112°. On the other hand, the torsion energy of 4 (12.5014kcal/mol) is larger than that of 3 (10.8217kcal/mol). This is due to the torsion energy between the eclipsing hydrogens, when the C=C on the 6 membered ring is hydrogenated.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

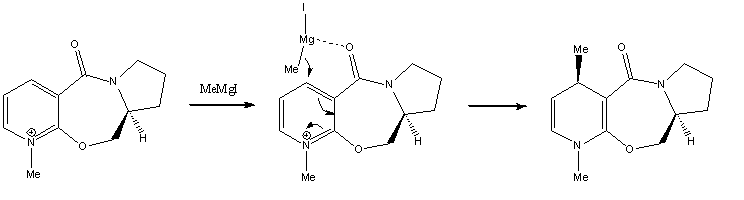
Reaction of N-methyl Pyridoxazepinone with Grignard Reagent

When the optically active derivative of prolinol 5 reacts with methyl magnesium iodide to alkylate the pyridine ring in the 4-position, the product has the absolute stereochemistry shown in 6. According to Schultz et al., this can be attributed to a chelation control, where the incoming Grignard reagent is coordinated to the electronegative oxygen of the carbonyl. Following coordination, the Me group is delivered to the pyridine ring via nucleophilic addition. Hence the geometry of the carbonyl group (above or below the plane of the aromatic ring) would determine the stereochemistry of the addition product.

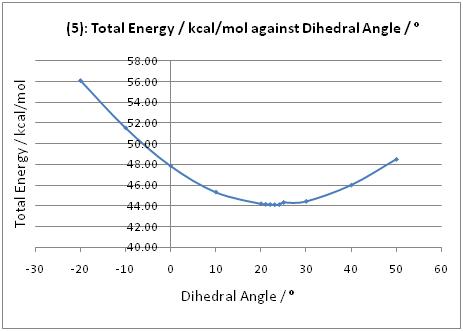
The geometry of the carbonyl group with respect to the aromatic ring was varied, and the energies of the molecules were recorded (see graph). The minimum energy was observed when the carbonyl group was 23.8° above the plane of the ring. Moreover, there were no low energy conformations with the carbonyl group below the plane of the ring. As such, the Grignard reagent would be chelated to the carbonyl group which is above the plane, and nucleophilic addition occurs on the top face of the ring, resulting in the product with the stereochemistry in 6.

The jmol applet of 5 is shown here. Note that the reagent MeMgI was not added, because ChemBio could not recognise Mg as an metal atom.

N-methyl pyridoxazepinone

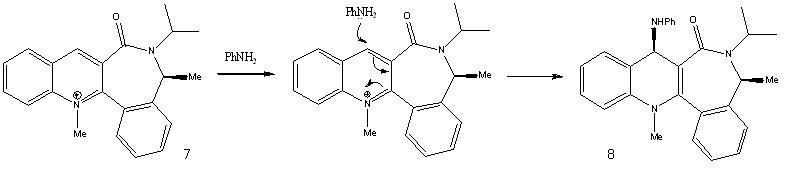
Reaction of N-methyl Quinolinium Salt with Aniline

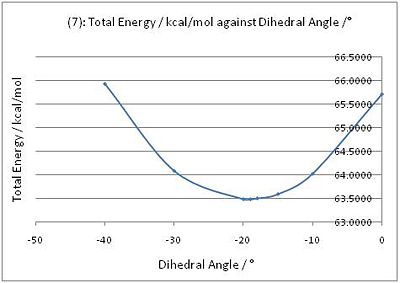
The pyridinium ring of 7 is reacted with aniline to form 8. According to Leleu et al., the incoming nucleophile would react on the opposite face with respect to the C=O group, assumed to originate from a steric control.

The geometry of the carbonyl group with respect to the aromatic ring was again varied, and the energies of the molecules were recorded. The minimum energy was observed when the carbonyl group was 19° below the plane of the ring. Hence, with a steric hindrance exerted by the carbonyl group below the plane of the ring, the aniline nucleophile would attack via the top face of the ring. This results in the stereochemistry as observed in product 8.

The jmol of 7 is shown here. In the optimisation of the geometry of 7, the reagent aniline was not included. However when included, the total energy of the system was in fact lower, by 6.39kcal/mol. This might be due to the nucleophilic aniline stabilising the electrophilic pyridinium ring, possibly through dipole interactions.

N-methyl Quinolinium Salt

Possible Improvements

ChemBio3D MM2 is a simple and less computationally intensive method of calculation. However, there is some trade off in the accuracy involved. A more intensive method like Gaussian density functional theory (DFT) would be able to give a more accurate energy and geometry optimisation.

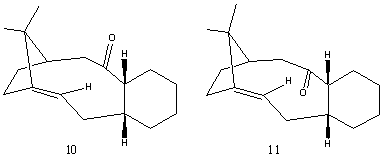
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Molecules 10 and 11 act as key intermediates in the total synthesis of Taxol, due to their high stability. On standing, 10 isomerises to 11, which is thermodynamically more stable. They are known as Atropisomers, which are stereoisomers resulting from hindered rotation about single bonds. Using Chem3D MM2, the total energy of 10 is determined to be 54.16kcal/mol, while that of 11 is 44.27kcal/mol.

In 10, the carbonyl is pointing upwards, close to the upward pointing Hydrogen atom. The cyclohexane ring is in a twist-boat conformation and there is a significantly higher strain in this twist-boat conformation as seen in the higher bend energy of 10 than 11 (16.55kcal/mol compared to 10.64kcal/mol). In 11, the carbonyl group is pointing downwards, away from the neighbouring upward pointing Hydrogen atom. Also, the cyclohexane ring is in a much more favourable chair conformation. This structure is in agreement with literature findings. This results in the overall lower energy of 11 and hence, 10 spontaneously isomerises to 11 on standing.

The unusual high stability of intermediates 10 and 11 is attributed to the stable bridgehead alkenes, which are termed hyperstable olefins. These alkenes are less strained than their parent saturated hydrocarbon, and they are generally trans-cycloalkene in medium/large sized rings. Hyperstable olefin have negative olefin strain energies (OS), where the strain energy of the olefin is less than its parent hydrocarbon. As such, they have lower than normal heats of hydrogenation. These olefins do not react easily (for example hydrogenation), which is suggested to be due to steric hindrance inhibiting approach to the reactant or catalyst. This property is useful in the synthesis of Taxol, since other groups can be reduced while retaining the hyperstable olefins.

Modelling Using Semi-empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene

Orbital Control of Reactivity

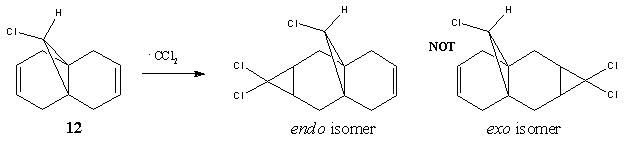
Orbital control of reactivity is observed in compound 12, 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene. The geometry of 12 is optimized and the energy and shape of the orbitals were analysed. Emphasis was placed on the Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO), since these orbitals control the reactivity of a molecule.

The reaction studied here is the electrophilic addition of electrophiles such as dicholocarbene with 12. As reported by Rzepa, the endo isomer is the only detectable product. This regioselectivity can be rationalised by molecular orbital (MO) theory.

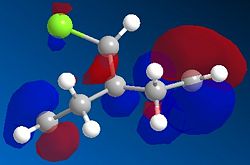
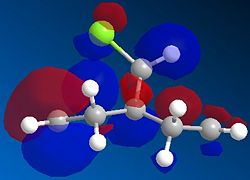
HOMO - 1	HOMO

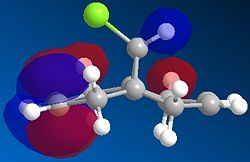
LUMO	LUMO + 1	LUMO + 2

With reference to the orbital diagrams above,

The HOMO shows a higher electron density at the syn-alkene compared to the anti-alkene (or exo; the C=C away from the C-Cl bond). This means that in the HOMO, the syn-alkene is more electron rich (hence more nucleophilic) compared to the anti-alkene. The HOMO-1 orbital shows a higher electron density at the anti-alkene. According to Rzepa et al., the orbital of the anti-alkene (HOMO-1) is stabilised relative to the syn-alkene orbital (HOMO), due to antiperiplanar overlap with the Cl-C σ* orbital (LUMO+1 here, although quoted as LUMO+2 in reference). Moreover, the syn-alkene also has a larger sterically accessible π orbital for electrophilic attack. Both arguments confirm the result obtained, that is, electrophilic addition occurs at the HOMO at the syn-alkene, giving the endo product.

There appears to be some discrepancy between literature and the results obtained here. This could be because the literature used the PM3 method for MOPAC calculation, while PM6 is used here. The conformation appears slightly bent in literature, whereas it is flat and symmetrical here. The LUMO+2 is reported to be Cl-C σ* orbital. We also know that since the HOMO and HOMO-1 are п orbitals, the LUMO and LUMO+1 are expected to be п* orbitals. However, it is not observed here, where the LUMO+1 is the Cl-C σ* orbital, and the LUMO+2 is the п* orbital. This might be caused by orbital mixing, where the Cl-C σ* orbital mixes with another σ* orbital of higher energy, resulting in the lowering of the energy of the Cl-C σ* orbital. Such orbital mixing might be present here due to the higher symmetry obtained in this optimisation.

Vibrational Frequencies of Molecules

The vibrational spectrum of 12 was studied, together with 13 which has the anti-alkene hydrogenated. The purpose is to determine

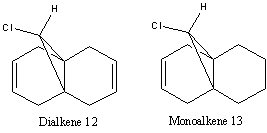
the influence of the C-Cl bond on the vibrational frequencies of this molecule.

The Infrared spectrum of the dialkene 12 and monoalkene 13 can be found at DOI:10042/to-2488 and DOI:10042/to-2487 respectively.

The C-Cl stretching frequency is determined by observing the animated motion of the molecule. There are many different frequencies which caused motion in the C-Cl part of the molecule, but the one identified as the stretching frequency involved the most distinct extension and compression of the C-Cl bond. The C-Cl stretching frequency is found to be 770.92cm^-1 in the dialkene 12, and 779.92cm^-1 in the monoalkene 13. This matches well with the literature stretching frequency of 780cm^-1.

There are two C=C stretches in the vibrational spectrum of 12, 1736.99cm^-1 for the anti-alkene and 1757.33cm^-1 for the syn-alkene. In 13, where the anti-alkene has been hydrogenated, there is only 1 C=C stretching frequency, at 1753.76cm^-1, corresponding to the syn-alkene stretch. The frequencies obtained for the syn-alkene are similar in both 12 and 13. All the C=C stretching frequencies obtained here are however much higher than the typical C=C stretch of 1670 - 1870 cm^-1. This might have been influenced by the C-Cl bond in the molecule. As noted above, there is a C-Cl σ* - exo π orbital interaction, which lowers the energy of the anti-alkene π orbital. A lowering of the orbital energy corresponds to a stronger bond, which in turn corresponds to a higher stretching frequency. Although not explicitly explained in literature, there might be a corresponding lowering of the energy of the syn-alkene, due to similar orbital mixing with higher energy orbitals, which stabilises the orbital of the syn-alkene, which therefore corresponds to a higher stretching frequency.

The anti-alkene has a lower stretching frequency, corresponding to a weaker bond. This might have the implication that the anti-alkene C=C bond should be easier to break, and hence the anti-alkene would react first, rather than the syn-alkene. There is hence a disagreement with the MO theory employed above, where the syn-alkene reacted with dichlorocarbene. A possible explanation for this apparent contradiction is that the stretching frequency takes into account the strength of both the σ and π C=C bond. The total bond strength of the σ and π carbon-carbon bond of the anti-alkene is therefore less than that of the syn-alkene, since the anti-alkene has a lower stretching frequency. However, when comparing reactivities, it is really only the π bond that is breaking, and MO theory would be more relevant, since it takes into account the energy of the particular molecular orbital involved. In this case, the syn-alkene is the HOMO, therefore it would react.

Structure-based Mini Project Using DFT-based Molecular Orbital Methods

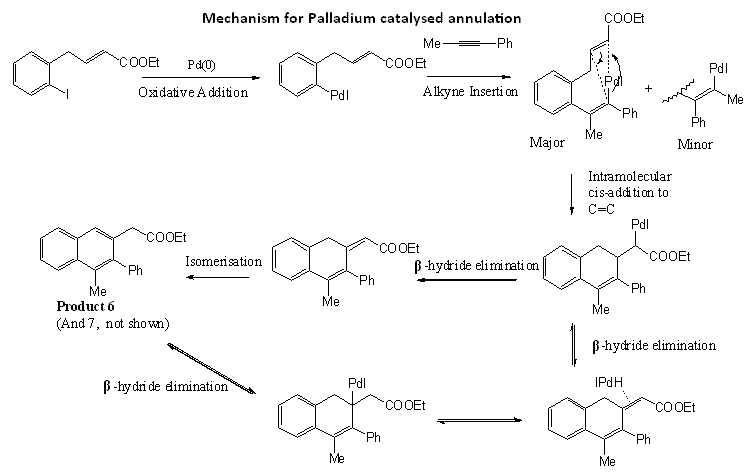
The reaction studied here is the synthesis of substituted naphthalenes by the Palladium-catalysed annulation of internal alkynes, by Q. Huang and R.C. Larock. This annulation process forms two C-C bonds in a single step, and the regioselectivity is examined in this mini project. This reaction was chosen for the project because it produces regioisomers which provides ¹³C NMR data for the isomers, and the products are not conformationally flexible.

Mechanism of reaction

The mechanism of the reaction is shown above, with reference to Huang and Larock's suggested scheme. Pd(0) undergoes oxidative addition and inserts into the C-I bond of the aryl iodide to form an arylpalladium species. This arylpalladium then adds to the alkyne and an intramolecular cis-addition to the C=C bond generates the fused cyclic rings. Beta-hydride elimination via one of two pathways would finally result in the products.

Since the alkyne contains two different substituents, two different products can be formed, due to the alkyne insertion in the 2nd step of this reaction. The arylpalladium intermediate is more likely to add to the less hindered end of the C-C triple bond. Hence, since the phenyl group is more bulky than the methyl group, the arylpalladium would more probably add to the carbon with the methyl substituent, forming the major product 6. However, Huang et al. reported that the regioselectivity appears to be significantly lower than normally observed in this synthesis. The regioisomers 6 and 7 were obtained in a 53:47 ratio.

Identification of Regioisomers

The objective of this project is to attempt to identify the two regioisomers produced in the reaction via various spectroscopic methods.

This is the information provided in the reference pertaining to products 6 and 7.

Ethyl (1-methyl-2-phenylnaphth-3-yl)acetate (6) and ethyl (2-methyl-1- phenylnaphth-3-yl)acetate (7). The reaction mixture was chromatographed using 20:1 hexane/EtOAc to afford 57 mg of a 53:47 mixture of regioisomers 6/7 as determined by 1H NMR spectral analysis of the yellow oil in a 75 % overall yield. 1H NMR (CDCl₃) for the major regioisomer 6: δ 1.26 (t, J = 7.2 Hz, 3H), 2.16 (s, 3H), 3.86 (s, 2H), 4.19 (q, J = 7.2 Hz, 2H), 7.20-7.52 (m, 8H), 7.73 (s, 1H), 7.79 (d, J = 4.8 Hz, 1H). 1H NMR (CDCl3) for the minor regioisomer 7: δ 1.13 (t, J = 7.2 Hz, 3H), 2.37 (s, 3H), 3.51 (s, 2H), 3.99 (q, J = 7.2 Hz, 2H), 7.20-7.52 (m, 7H), 7.67 (s, 1H), 7.83 (dd, J = 1.2, 4.8 Hz, 1H), 8.03 (d, J = 8.0 Hz, 1H). 13C NMR (CDCl₃) for the mixture δ 14.3, 14.4, 16.8, 17.7, 40.6, 40.6, 60.8, 61.1, 124.6, 125.3, 125.8, 125.9, 126.2, 126.5, 127.2, 127.2, 127.3, 127.6, 128.4, 128.5, 128.6, 128.9, 129.9, 130.4, 131.2, 131.9, 132.0, 132.2, 132.5, 132.6, 132.9, 132.9, 139.3, 139.8, 140.4, 140.8, 171.9, 172.1; IR (neat, cm^-1) for the mixutre 3056, 3022, 2981, 2934, 2870, 1731, 1599, 1572; HRMS Calcd for C₂₁H₂₀O₂: 304.1463. Found: 304.1467.

The two products can be identified using ¹H NMR Spectroscopy, since the protons are in different chemical environments. The integral of the peaks can be used to tell apart the peaks, since product 6 is expected to be the major product. Infrared analysis would be able to show what functional groups are in the compounds. However, since both products have similar functional groups, infrared analysis would not help in differentiating the products. Lastly, ¹³C NMR can be employed to distinguish between the different C chemical environments in the products. The ¹³C NMR data provided above is for the mixture of products, and no assignment was done for the peaks.

¹³C NMR Prediction using Gaussian

Below is the ¹³C NMR data, based on the predicted ¹³C spectra using the Gauge Including Molecular Orbital (GIAO) with Gaussian Density Functional Theory (DFT) method. The carbons are numbered as in the Gaussian log file, for easy reference. The related files can be found here:

For 6, DOI:10042/to-2511

For 7, DOI:10042/to-2510

Predicted 13C NMR data

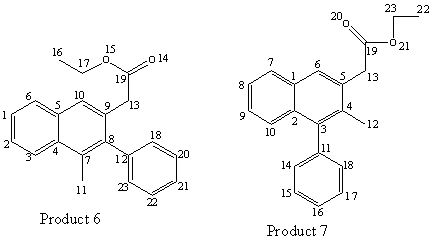
C on Pdt6	δ/ppm	C on Pdt7	δ/ppm
16	14.7	22	14.5
11	19.3	12	19.9
13	39.9	13	39.6
17	61.2	23	61.1
3	122.3	8	121.8
2	122.8 (deg=2)	9	122.2
1	122.8 (deg=2)	6	122.4
21	123.6	10	123.6
22	123.8	16	123.8
10	124.0	15	124.4
20	124.3	17	124.5
6	125.2	7	125.1
4	127.6	14	127.0 (deg=2)
5	127.8	1	127.0 (deg=2)
23	128.1	18	127.2
18	129.6	2	128.3
9	129.9	5	129.0
7	132.1	4	131.0
12	138.1	3	138.0
8	138.5	11	138.3
19	167.1	19	166.9

The ¹³C NMR predicted are very similar in both compounds, and it appears improbable to assign the peaks to those given in literature. There are, however, a few differences between the two spectra.

Firstly, there exists a degeneracy of 2 for the spectrum of 6 at δ122.8ppm and for the spectrum of 7 at δ127.0ppm. This is the clearest difference between the two spectra.

Next C-10 of 6 has chemical shift of δ124.0/ppm while C-6 of 7 has chemical shift of δ122.4/ppm. C-18 of 6, has chemical shift of δ129.6/ppm while C-18 of 7 has chemical shift of δ127.2/ppm. These differences are noticeable, but since the mean error is 1.4ppm for sp³ carbon and 5.1ppm for sp² carbon, these differences are not significant.

Apart from the degeneracy difference and the slight difference in chemical shifts mentioned above, the two spectra look highly similar, and cannot be differentiated. It was also difficult to assign the predicted chemical shifts to the literature chemical shifts, since the peaks were not assigned to each separate product, and the chemical shifts lie very close to each other.

Hence, although the ¹³C NMR prediction by the GIAO approach using the mPW1PW91/6-31G(d) as standard was in computational terms highly accurate, the error involved in the calculations was still too large to be used in this case, to differentiate between highly similar isomers.

Optical Rotation

Since the ¹³C NMR cannot be used to differentiate the isomers, an attempt was made to determine if the two isomers could be identified using optical rotation. The job was submitted to the ChemistryLab, even though this molecule was relatively big and the job was expected to take a long time. The calculations took more than 23 hours each, but no result was obtained. For both molecules, the convergence criterion were not met and the run was terminated.

The related files can be found here:

For 6, DOI:10042/to-2535

For 7, DOI:10042/to-2534

Separation of products

The products could be separated by chromatography, by Column Chromatography or High Performance Liquid Chromatography. High resolution separation can be obtained via this method and it would be possible to find better solutions to distinguish between the isomers once they are separated.

Conclusion

In conclusion, the Gaussian NMR prediction method cannot be used here to distinguish between the isomers. Also, since this molecule is large and non-chiral, it is difficult to find other methods to identify the two highly similar regioisomers. ¹H NMR appears to be a possible option, since the chemical shifts, coupling, and integral would help in identifying the regioisomers.