Rep:Mod1:summeisiuyee

Modelling using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

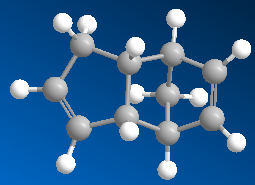
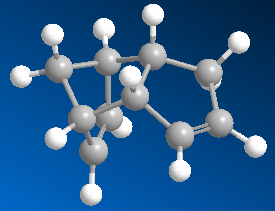
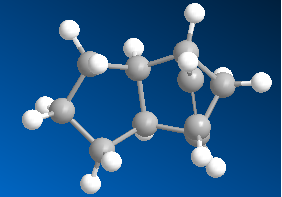
Via Diels Alder reaction, cyclopentadiene acts as both diene and dienophile to form dicyclopentadiene at room temperature which results in two ismomers: the exo and endo dimers as shown above. The highly favoured endo dimer can proceed to given two dihrdro derivatives via hydrogenation. Tetrahydro derivative can only be formed after prolonged hydrogenation.

The cyclodimerisation and hydrogenation can be due to either thermodynamic (product stability) or kinetic (transition state stability) factors. On the basis of the results obtained from the molecular mechanics technique, conclusion can be drawn to whether the cyclodimerisation of cyclopentadiene and the hydrogenation of the dimer is kinetically or thermodynamically controlled.

The reactant were drawn in Chembio3D and their geometries were optimised by the MM2 method force field option in order to obtain the minimized energies of the products.

Comparison Of The Two Dimers

	Exo Dimer 1	Endo Dimer 2
Images
Jmol
Stretch	1.2859	1.2439
Bend	20.5871	20.8701
Stretch-Bend	-0.8379	-0.8344
Torsion	7.6717	9.5092
Non-1,4 VDW	-1.4353	-1.5636
1,4 VDW	4.2335	4.3273
Dipole/Dipole	0.3778	0.4488
Total Energy	31.8829 kcal/mol	34.0013 kcal/mol

Analysation 1

From the table above, the minimised energy of the exo dimer 1 is lower than the energy of the endo dimer 2 which means the exo dimer is more stable in terms of energy and hence is the thermodynamic product. However, the kinetic product endo dimer 2, has a more stable transition state as a lower activation energy is required to overcome the barrier compare with exo dimer 1. According to the Endo Rule, this favours the Diels Alder reaction and so the kinetic product endo dimer 2 will be the major product of this reaction and this reaction is thus under kinetic control.

The two hydrogenated products 3 and 4 were dalso rawn in Chembio3D and their geometries were optimised by the MM2 method force field option in order to obtain the minimized energies of the products.

Comparison Of The Two Dihydro Derivatives

	Dihydro 3	Dihydro 4
Images
Jmol
Stretch	1.2797	1.1004
Bend	19.8615	14.5210
Stretch-Bend	-0.8384	-0.5462
Torsion	10.8144	12.5091
Non-1,4 VDW	-1.2242	-1.0548
1,4 VDW	5.6359	4.4963
Dipole/Dipole	0.1620	0.1407
Total Energy	35.6910 kcal/mol	31.1665 kcal/mol

Analysation 2

From the above table, the minimised energy of the endo dihydro derivative 4 is lower in energy than the exo dihydro derivative 3 which means the endo product is more stable in terms of energy and hence is the thermodynamic product. The fact that the calulated energy of transition state of 4 is higher than that of 3 suppports the above statement that the formation of the hydrogenated product 4 is under thermodynamic control.

It is quite easy to spot that the main contribution to the difference in energy between the two products comes from the bending energy. The bond angle of the C=C double bond is ~107 degree for 3 while the bond angle of the C=C double bond of 4 is ~112 degree. Since the bond angle of product 4 is closer to the ideal value for C=C double bond (i.e. 120 degree), this molecule is less strained and thus more favoured to be the major product.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD⁺ Analogue)

Two examples of nucleophilc additions to a pyridium ring are investigated here. The first one includes reacting the optically active prolinol 5 with the Grignard reagent methyl magnesium iodide to alkylate the 4th-position of the pyridine ring to form product 6. The other example includes derivating the pyridinium ring of reactant 7 to product 8. On the basis of the results obtained from the molecular mechanics technique, the origin of the stereocontrol in the foration of product 8 can be spectulated.

Prolinol 5, product 6 and its enantiomer were drawn using the Chembio3D program and their geometries were optimised by the MM2 method force field option in order to obtain the minimized energies of them.

Minimised Structures of 5, 6 and its enantiomer

	Prolinol 5	Product 6	Product 6 Enantiomer
Images
Jmol
Stretch	2.0467	2.2595	2.2813
Bend	14.2321	16.3532	16.3938
Stretch-Bend	0.1320	0.3468	0.3355
Torsion	5.1100	5.6372	5.4760
Non-1,4 VDW	-0.5892	-0.3094	-0.3165
1,4 VDW	16.5399	17.5024	17.5342
Charge/Dipole	9.3455	-	-
Dipole/Dipole	-3.9886	-4.3070	-4.3031
Total Energy	42.8283 kcal/mol	37.4826 kcal/mol	37.4012 kcal/mol

Analysation 1

By using the MM2 method, two configurations of 5 were found with different stereochemistry -- the more optimised one with C=O group coplanar to the aromatic ring and the other one tilted above the plane at a degree of ~35.

From the table above, the minimised energy of the product 6 (addition from above plane) and that of its enantiomer (addition from below plane)are very close to each other. This suggests that the above statement is correct that the configuration of 5 with C=O coplanar to the aromatic ring is more optimised. Although the values are very close to each other, the energy difference between the two suggests that addition is from below the plane as the enantiomer has a lower minimised total energy. This maybe due to the steric hindrance between the nucleophile and the carbonyl oxygen above the plane from the less favoured configuration of 5. However, because of the chelation between the carbonyl oxygen magnesium of the nucleophile, addition from above the plane is favoured and so product 6 will be formed under kinetical control.

Reactant 7, product 8 and its enantiomer were drawn using the Chembio3D program and their geometries were optimised by the MM2 method force field option in order to obtain the minimized energies of them.

Minimised Structures of 5, 6 and its enantiomer

	Reactant 7	Product 8	Product 8 Enantiomer
Images
Jmol
Stretch	3.6769	4.1235	4.1856
Bend	11.3289	18.4089	18.9837
Stretch-Bend	0.4004	0.8029	0.8387
Torsion	10.5902	4.8458	5.7453
Non-1,4 VDW	3.8770	1.67944	3.3784
1,4 VDW	29.3046	34.1034	34.0777
Charge/Dipole	3.3169	-	-
Dipole/Dipole	-34.8743	-6.7170	-6.3225
Total Energy	57.6207 kcal/mol	57.2468 kcal/mol	60.8868 kcal/mol

Analysation 2

From the table above, the minimised energy of the product 8 (addition from above plane) is lower than its enantiomer (addition from below plane) and more stable and hence is the major product. This is supported by visuallising the picture showing the optimised reactant 7. From the picture above, it is easy to spot out that C=O group is slightly below the aromatic ring and so nucleophilic addition is expected to attack from above the ring to minimised steric hindrance. Thus product 8 is formed under thermodynamic control.

References

1) A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

9 and 10 are the key intermediates for the total synthesis of Taxol with the carbonyl group pointing upwards for the former intermediate and the carbonyl group pointing downwards for the latter one. On the basis of the results obtained from the molecular mechanics technique, conclusion can be drawn to whether the most stable ismoer is 9 or 10 - whether the carbonyl group should be pointing upwards or downwards.

Intermediates 9, 10 and its hydrogenated form were drawn using the Chembio3D program and their geometries were optimised by the MM2 and MMFF94 method force field options in order to obtain the minimized energies of them.

Comparison Of The Two Intermediates And The Hydrogenated Form

	Intermediate 9	Intermediate 10	Hydrogenated 10
Images
Jmol
Stretch	3.0692	2.5772	3.1473
Bend	19.8179	13.4012	18.1098
Stretch-Bend	0.3042	0.3373	0.6814
Torsion	21.3779	21.0758	23.1188
Non-1,4 VDW	0.3251	-0.6315	0.8434
1,4 VDW	15.0155	13.5997	16.6920
Dipole/Dipole	0.0705	0.2607	0.0000
Total Energy by MM2	59.9793 kcal/mol	50.6204 kcal/mol	62.5927 kcal/mol
Total Energy by MMFF94	82.3381 kcal/mol	66.5773 kcal/mol	-

From the above table, comparing the Total Energy by MM2 and MFF94: it shows that comparison of MM2 and MMFF94 gives very different energies with the energies obtained by MMFF94 is in average ~20 kcal/mol higher than the energies obtained by MM2. This suggests that MM2 is a better model as using it a more stable compound can be obtained.

Comparing intermediate 9 and 10: both of the computing technique agrees that the intermediate 10 has a lower energy than the intermediate 9 and hence intermediate 10 is a more stable intermediate which favours thermodynamic control. The greatest contribution on the difference in energy between the two intermediates is from bending energy which is the strain on the system due to the change in geometry of the carbonyl group.

Comparing intermediate 10 and the hydrogenated product: the total energy of the hydrogenated product by MM2 is higher than intermediate 10 which suggests that the hydrogenation of the alkene is not thermodynamically favourable to proceed and hence this matches the literature that the 'hyper stable' alkene hydrogenates very slowly.

References

1) S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319. DOI:10.1016/S0040-4039(00)92617-0

2) J. G. Vinter and H. M. R. Hoffman, J. Am. Chem. Soc., 1974, 96, 5466 and 95, 3051. DOI:10.1021/ja00824a025

Modelling Using Semi-Empirical Molecular Orbital Theory

There are 2 parts in this session. The pros and cons of using purely mechanical molecular model will be shown in part 1. In the case of endo stereoselectivity in secondary orbital interactions, as Molecular Mechanics approach is not useful, electronic aspects of reactivity will be illustrated. The explicity of the electrons in molecules, the influence on bonds by electrons and spectroscopic properties will all be considered.

In part 2, the influence of Cl-C bond on the vibrational frequencies of molecule 12 and its hydrogenated version will be calculated and compared. Density functional approach will be introduced as the most relable procedure for obtaining vibrations.

Regioselective Addition of Dichlorocarbene

Part 1: Molecular wavefunction of compound 12 will be obtained by applying the electronic method MOPAC/PM6 after running MM2 to clean up the geometry. As the HOMO is the most nucleophilic, it is a good indication of which of the two alkenes in compound 12 will the dichlorocarbene react to.

Compound 12 drawn using the Chembio3D program and their geometries were optimised by the MM2 method force field option in order to obtain the minimized energies of them.

MM2 Minimisation Of Compound 12

	Compound 12
Image
Jmol
Stretch	0.6216
Bend	4.7232
Stretch-Bend	0.0394
Torsion	7.6824
Non-1,4 VDW	-1.1012
1,4 VDW	5.8256
Dipole/Dipole	0.1119
Total Energy	17.9030 kcal/mol

MOPAC/PM6 was then used to approximate the valence-electron molecular wavefunction including the HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2. The heat of formation of the HOMO formed was 19.74000 kcal/mol .

Visualisation Of Molecular Orbitals, Compound 12

Structure of optimised Compound 12	HOMO	HOMO-1
LUMO	LUMO+1	LUMO+2

Analysation

In order to determine which alkenes will the dichlorocarbene react to, the electronic effects must be considered to find out the more reactive alkene. Among the above molecular orbitals, HOMO alkene which has the chlorine closer to its side has the most concentrated electrons cloud and so it is the most nucleophilic (ie, most susceptible to electrophilic attack) and hence the dichlorocarbene will attack that alkene.

This can be supported by the fact that the other alkene in Compound 12 is more stable due to the antiperiplanar interactions between C-Cl sigma star orbiral and its occupied pi orbital. As it is more stable, it is more reluctant to have reaction with the dichlorocarbene and hence the alkene on the chlorine side is more reactive.

Some may counter argue that the dichlorocarbene should attack the alkene that is further away from chlorine due to steric reasons. However, as the sizes of H and Cl are both small, the steric effect is not strong enough to overcome the antiperiplanar interactions argument and so in conclusion, the dichlorocarbene will react on the alkene closer to the chlorine.

Part2: 12 B3LYP/6-31G(d,p)in Gaussian was used to calculate the stretching frequencies of the PM6 optimised geometries of compound 12 and monocarbene version of compound 12.

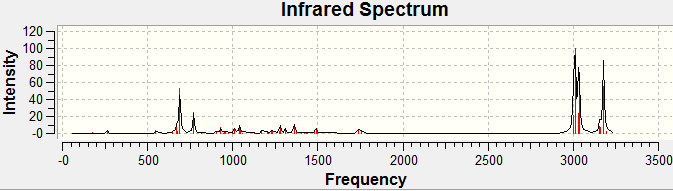
IR spectra of the Dicarbene:

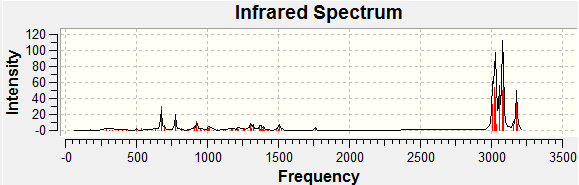
IR spectra of the Monocarbene:

The table below shows the stretching frequencies observed in both the dicarbene and monocarbene of compound 12 of C=C(endo & exo) and C-Cl bonds.

Stretching Frequencies (cm^-1)

	Dicarbene	Monocarbene
C=C (endo)	1757.38	1758.06
C=C (exo)	1737.14	-
C-Cl	770.872	774.962

From the result above, the c=c exo bond has a lower energy than the endo one supports the statement above that the alkene that is further away from the chlorine is more stable than the other and thus enhancing the suggestion that the alkene that is closer to the chlorine reacts with the dichlorocarbene.

The exo and endo bonds are allowed to be clearly differentiated by using the density functional approach. The presence of HOMO on the endo alkene was enhanced by the fact that the endo C=C stretching frequency is higher than the exo. It may be useful to note that there is also a little difference in the stretching frequencies of C-Cl bonds between the dicarbene and monocarbene.

References

1) B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447

Structure based Mini project using DFT-based Molecular orbital methods

In the mini project, different approaches such as the computational method from Gaussian and Chembio3D, ¹³C NMR chemical shift, ³J H-H coupling constants, IR spectra and optical rotation etc have to be considered to be used so as to confirm the product from experiment (literature) fit the computational calculatedand hence a correct model has been made.

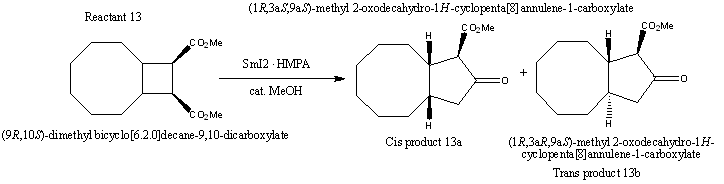
Reaction of (9R,10S)-dimethyl bicyclo[6.2]decane-9,10-dicarboxylate (12a) with Samarium(II) in the presence of HMPA

There will be a ring expansion when Reactant 13 reacts with Sm(II) in the presence of HMPA with a catalytic amount of methanol which will result in formation of both cis and trans products in a ratio of 1:1.5 (68%).

Reactant 13

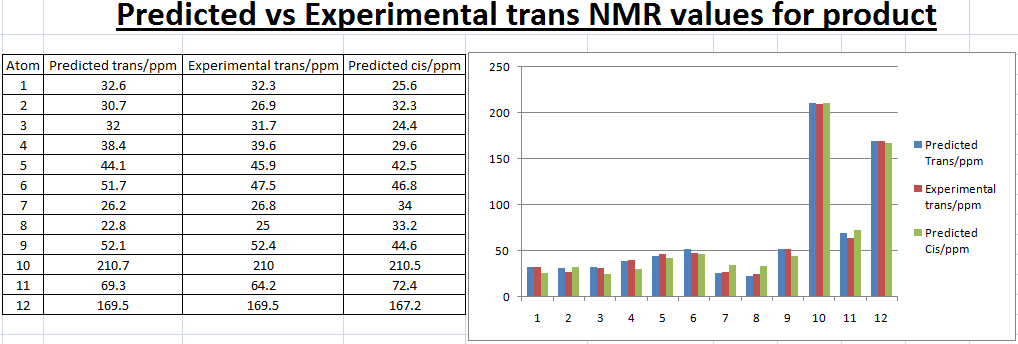
The predicted ¹³C NMR spectra was obtained by GIAO approach using quantum mechanical density functional theory which the molecule was first drawn in Chembio3D to perform an initial refinement of the 3D geometry using MM2.

Comparison Of The Two Isomers

	Cis 13a	Trans 13b
Images
Jmol
Stretch	1.5676	1.2810
Bend	11.4421	10.4777
Stretch-Bend	0.3983	0.3786
Torsion	9.6809	11.2228
Non-1,4 VDW	-1.7332	-3.1418
1,4 VDW	12.0670	12.2415
Dipole/Dipole	4.4994	4.4816
Total Energy	37.9222 kcal/mol	36.9413 kcal/mol

The optimised geometry then reached the DFT=mpw1pw91 by Gaussian program. NMR can then be obtained after calculation by supercomputer.

Images
Jmol
Carbon	Calculated Chemical Shift/ppm
1	37.4
2	32.3
3	24.4
4	29.6
5	42.5
6	43.1
7	34.0
8	33.2
9	44.6
10	210.5
11	72.4
12	167.2
16	55.2

NMR and the corresponding structure with atoms all labelled

Structure of Reactant 13	NMR of Reactant 13
Structure of Cis Product 13a	NMR of Cis Product 13a
Structure of Trans Product 13b	NMR of Trans Product

Since the compound has less than 25 non hydrogen atoms, it is regarded as small and IR specta of both cis and trans products were predicted by submitting the optimised geometry to the supercomputer and using Gaussien program to view the resulted IR specta.

Bond	Calculated Streching Frequency/cm-1	Reference 13a Frequency/cm-1	Reference 13b Streching Frequency/cm-1
C=O Ester	1802.71 (13a); 1821.36 (13b)	1732	1732
C=O Ketone, cyclic 5-membered	1849.66 (13a), 1849.08 (13b)	1755	1755

Analysation

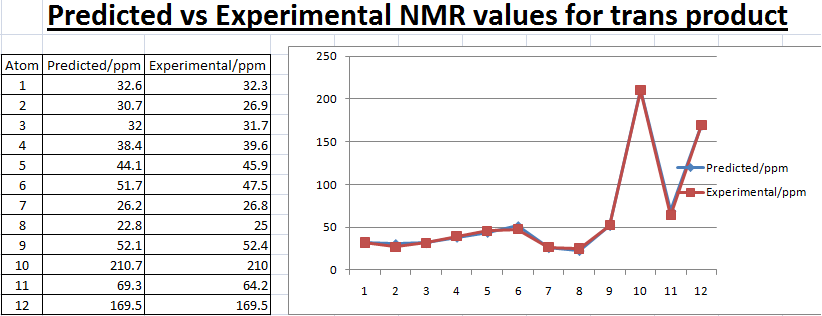
By using Molecular modelling MM2, minimised 13b has a lower energy than 13a suggesting 13b is thermodynamically favoured as from literature value the ratio of 13a:13b=1:1.5. Bar charts and line charts were used to show that the calculated chemical shift was well modelled as they are really close to literature values. This confirms that the two isomers 13a and 13b were both formed by the reaction. However, IR values do not match well with the reference which suggests that modelling of the molecules can still be improved by further minimzing the energy of the initial molecule.

References

1) I. Shinohara, H. Nagaoka, Tetrahedron Letters, 7 (45), 2004, 1495-1498 DOI:10.1016/j.physletb.2003.10.071

Additional References

1) DOI:10042/to-7393 -NMR of Reactant 13

2) DOI:10042/to-7396 -NMR of 13a

3) DOI:10042/to-7399 -NMR of 13b

Conclusion

The computational modelling is best performed by rearraging the initial structure of the molecule until the minimum energy is obtained. The best example comes from the cycloalkane example as if the molecule is not arranged in chair form, the energy obtained would be nearly 10 times bigger the the minimum energy we can get. The trick is that we move every atom the farest away from each other and by that, the minimum energy could be obtained and the result for further analysis such as IR or NMR would be much closer to the literature value.