Jump to content

Rep:Mod1:sherwingoh

From ChemWiki

Molecular Mechanics Modelling

Molecular mechanics is a method of 3D molecular modelling which optimises molecular geometry to an energy minimum and analysing the vibrational and bonding contributionts to the total energy. In this exercise, Allinger's MM2[1] force field is employed by ChemBioDraw Ultra 12.0 to conduct energy minimisation and geometry optimisation to identify the stable conformations of molecules. This information is utilised to deduce and explain reaction mechanisms and selectivity in products.

Hydrogenation of Cyclopentadiene Dimer

Dimerisation of Cyclopentadiene

Wilson et al[2] showed that cyclopentadiene dimerises rapidly at room temperature by the Diels-Alder[3] reaction to produce the endo dimer 2 as the only product, with no formation of the exo dimer 1.

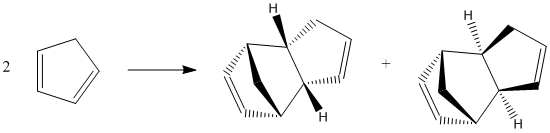
A comparison of the energies of the possible dimerisation products was conducted to determine their relative stabilities, as shown in the table below.

Table 1: Energies of Cyclopentadiene Dimers
Dimer Energy / kJ mol-1
exo-dicyclopentadiene 1
Cyclopentadiene Dimer 1
 133.4
endo-dicyclopentadiene 2
Cyclopentadiene Dimer 2
 142.3

The energy of the exo dimer 1 is lower than that of the endo dimer 2, indicating that the exo dimer 1 is the thermodynamically favourable product for cyclopentadiene dimerisation. This is consistent with experimental observation from Herndon et al[4] which indicates that the exo isomer is the slightly more stable of the dicyclopentadienes.

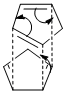
However, the endo dimer 2 is the kinetically favourable product, via a bispericyclic transition structure reported by Caramella et al[5]. The selection of the endo product follows Alder's endo rule[6] through the "maximum accumulation of unsaturated centers", shown on the right, which leads to a lower energy transition state and hence a more rapid reaction. This selectivity is also explained by Woodward-Hoffmann rules and secondary orbital interactions[7] for pericyclic reactions.

As the Diels-Alder[3] reaction is irreversible, the kinetic endo product dominates. Hence, it can be concluded that the dimerisation of cyclopentadiene is kinetically controlled.

Hydrogenation of Cyclopentadiene Dimer

Hydrogenation of endo-dicyclopentadiene 2 initially only gives the dihydro derivative 4[8] , without any of the dihydro derivative 3. Complete hydrogenation to the tetrahydro product is only possible after prolonged periods.

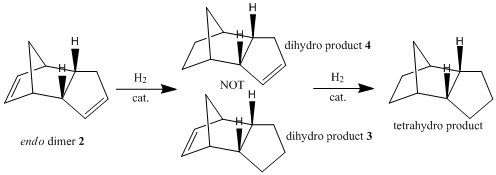
The energies of the possible dihydro products of hydrogenation were compared, as shown in the table below.

Table 2: Contributions to Energies of Hydrogenation Products
Hydrogenation Product Stretching / kJ mol-1 Bending / kJ mol-1 Torsion / kJ mol-1 Van der Waals / kJ mol-1 Hydrogen Bonding / kJ mol-1 Total Energy / kJ mol-1
Product 3
Cyclopentadiene Dimer 3
 5.4 82.9 45.5 23.6 0.7 149.5
Product 4
Cyclopentadiene Dimer 4
 4.6 60.8 52.4 18.9 0.6 130.5

Comparing the energy contributions from vibration and bonding modes, dihydro derivative 4 has significantly lower bending strain than dihydro derivative 3. This can be attributed to the higher bond and angle strain experienced by the norbernene C=C bond as compared to the cyclopentene C=C bond, since the norbernene C=C bond forms part of the bicyclic structure with the bridgehead methylene group. The norbernene C=C bond has a longer bond length and weaker bond strength than the cyclopentene C=C bond[9], thus explaining why the norbernene C=C bond is hydrogenated more easily to from dihydro derivative 4.

Overall, the hydrogenation product 4 has a lower total energy than the hydrogenation product 3, which corroborates with DFT simulations from Zou et al[9]. Thus, the thermodynamically favourable dihydro derivative of dicyclopentadiene is product 4. This observation is supported by experimental data which shows that the hydrogenation of the double bond in the norbornene ring of dicyclopentadiene to form dihydro derivative 4 has a reaction rate several times higher than the same hydrogenation in the cyclopentene ring to form dihydro derivative 3[10].

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ analogue)

Reaction of Pyridinium Ring in N-methyl Pyridoxazepinone 5 with Grignard Reagent

The nucleophilic addition of Grignard reagents[11] to N-methyl salts of pyridoxazepinone 5[12] is highly regio- and stereo- selective.

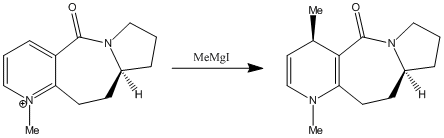
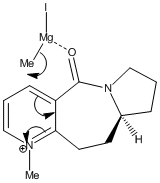
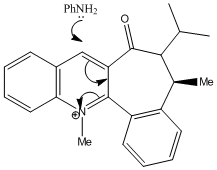
In the reaction of methyl magnesium iodide (MeMgI) with N-methyl pyridoxazepinone 5, Shultz et al[12] postulated that the electropositive Mg atom of the Grignard reagent[11] coordinates to the electronegative O atom of the amide functionality, as shown on the right. Coordination then allows conjugate delivery of the Me group to the top face of the adjacent C-4 position on the pyridinium ring via nucleophilic addition to generate the observed product with high regio- and stero- selectivity.

A comparison of the energies of different conformations of N-methyl pyridoxazepinone 5 was conducted to determine the most stable conformation. This is the equilibrium conformation of the molecule, which controls the mechanism of its reaction with MeMgI. Emphasis was placed on the geometry of the C=O bond of the amide functionality with respect to the aromatic pyridinium ring, as it influences the stereochemical outcome of the reaction.

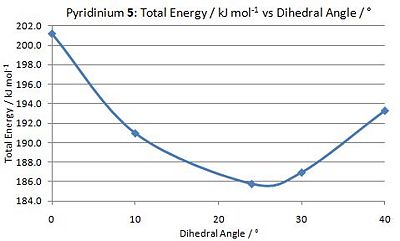
The geometry of N-methyl pyridoxazepinone 5 was optimised with respect to the dihedral angle between the O atom of the amide C=O functionality and the C-4 position of the pyridinium ring. A graph was plotted to determine the optimal angle at which the total energy of 5 is minimal. As shown in the graph on the left, the optimal dihedral angle between the O atom of the amide functionality and the C-4 position on the pyridinium ring is 23.8o, with the C=O bond pointing above the plane of the ring.

Click here to view a Jmol Applet[13] of N-methyl pyridoxazepinone 5.

This observation is useful in explaining the regio- and stereo- selectivity of the nucleophilic addition by MeMgI on N-methyl pyridoxazepinone 5. As the O atom of the amide functionality is angled 23.8o above the plane of the ring, coordination by the Mg atom of MeMgI results in the molecules being orientated such that the Me group of MeMgI is positioned directly above the C-4 position of the pyridinium ring. Nucleophilic attack by the Grignard reagent from the top face of the C-4 position is thus favoured.

Reaction of Pydridinium Ring in N-methyl Quinolinium Salt 7 with Aniline

Similarly, nucleophilic addition of aniline to N-methyl quinolinium salt 7[14] is highly regio- and stereo- selective.

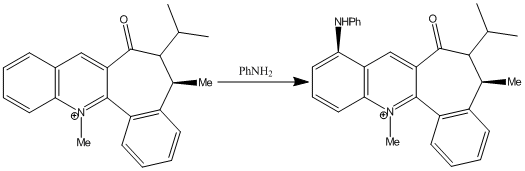
In the reaction of N-methyl quinolinium salt 7 and with piperidine and benzyl amine, Leleu et al observed that the amines react on the opposite face with respect to the C=O bond of the amide functionality, and attributed the diastereofacial selectivity to steric control exerted by the C=O group[14].

A comparison of the energies of different conformations of N-methyl quinolinium 7 was conducted to determine the equilibrium conformation of the molecule. The geometry of the C=O bond of the amide functionality with respect to the aromatic pyridinium ring was the focus of the study, as it exerts stereochemical control of the reaction with aniline, which proceeds by the mechanism shown on the right.

The geometry of N-methyl quinolinium 7 was optimised with respect to the dihedral angle between the O atom of the amide C=O functionality and the C-4 position of the pyridinium ring. As shown in the graph on the left, the optimal dihedral angle between the O atom of the amide functionality and the C-4 position on the pyridinium ring is -18.1o, indicating that the C=O bond is pointing below the plane of the ring.

Click here to view a Jmol Applet[13] of N-methyl quinolinium 7.

This observation is useful in explaining the regio- and stereo- selectivity of the nucleophilic addition by aniline on N-methyl quinolinium 7. As the O atom of the amide functionality is angled 18.1o below the plane of the ring, nucleophilic attack by aniline from the bottom face of the ring is electronically and sterically hindered. Hence, nucleophilic attack by the aniline from the top face of the C-4 position occurs instead.


Possible Improvements

Improvements to the computational calculations can be made by more accurate methods instead of molecular mechanics with MM2[1] force field. Dewar's MOPAC[15] method and Pople's Gaussian[16] density functional theory (DFT)[17]] method are more computationally intensive, but take into account the molecular orbitals and electronic structure of the molecules, and are thus give better calculations of the energy and geometry optimisation. In addition, Gaussian[16] is capable of minimising the energy of two molecules with respect to each other in the same computation. This is useful in examining reaction mechanisms since the optimal conformation of the reacting molecules can be determined, and thus the regio- and stere- chemistry of the reaction can be explained. ChemBioDraw Ultra 12.0 is unable to do this for the reactin of molecule 5 with MeMgI, as Mg cannot be recognised by the 3D-drawing program. For the reaction between molecule 7 and aniline, the program only optimises the energy of the molecules individually, but not with respect to each other.

Improvements to both the experimental and computational procedure can be made by introducing bulky groups to the alkyl rings to make them less conformationally flexible. Experimentally, this would improve the regio- and stereo- selectivity of reaction, as there is a larger energy barrier to ring-flipping of the cycloalkanes, thus restricting its conformation to the equilibrium position. An increase in rate would also result, as there is no need for reacting molecules to rotate into the correct orientation for reaction. The addition of ring-locking groups also benefits computational calculations as it is easier to optimise the molecule when there is a specific ring conformation which is preferred.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

15,15-Dimethyl-tricyclo[10.2.1.04,9]pentadec-11-en-3-one atropisomers 10/11 are a key intermediate in the total synthesis of Taxol[18] due to hyperstability[19].

Atropisomerism in 10/11

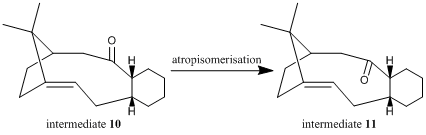
Atropisomers are stereoisomers in which steric strain hinders rotation about single bonds and prevents interconversion of isomers[20]. Paquette et al showed that intermediate 10 isomerises to intermediate 11 on standing[21].

The energies of the atropisomers were compared, as shown in the table below.

Table 3: Contributions to Energies of Atropisomers
Hydrogenation Product Stretching / kJ mol-1 Bending / kJ mol-1 Torsion / kJ mol-1 Van der Waals / kJ mol-1 Hydrogen Bonding / kJ mol-1 Total Energy / kJ mol-1
Intermediate 10
Taxol 10
 11.7 69.3 86.3 58.5 0.8 226.7
Intermediate 11
Taxol 11
 10.8 44.7 82.8 52.3 -0.8 185.4

Comparing the energy contributions from the vibration and bonding modes, the atropisomer 10 has significantly higher bending strain than atropisomer 11. This can be attributed to the different conformations of the cyclohexane ring in the isomers. In intermediate 10, the cyclohexane ring is locked in a strained high-energy twist-boat conformation with the carbonyl group pointing above the plane of the ring, while the cyclohexane ring in intermediate 11 has a lower energy chair conformation with the carbonyl group pointing below the plane of the ring[21].

Overall, the total energy of intermediate 11 is lower than that of intermediate 10. Therefore, upon standing, intermediate 10 spontaneously isomerises to intermediate 11.

Hyperstability of 10/11

Maier and Schleyer defined "hyperstable olefins" as alkenes which are less strained than their parent saturated hydrocarbons[19]. These isolabe olefins are generally bridgehead olefins contained in a trans-cycloalkene unit with at least 8 carbon atoms, as first recognised by Wiseman[22].

Hyperstable olefins are characterised by their negative olefinic strain (OS) energies, defined as the extra strain associated with the double bond compared to the parent saturated hydrocarbon. OS is calculated by subtracting the total strain energy of the most stable conformer of the parent hydrocarbon from that of the alkene, and is experimentally related to the heat of hydrogenation[19].

Hyperstable alkenes are unreactive due to a special stability conferred by the cage structure of the olefin, and also the greater strain of the parent hydrocarbon, thereby conferring resistance to hydrogenation[19]. Hence, they are useful in total synthesis, especially when there is a need for reduction of other functional groups.

Semi-Empirical Molecular Orbital Theory Modelling

Semi-empirical Molecular Orbital Theory is a method of 3D molecular modelling which considers electronic properties of molecules in computing optimal geometry and deriving spectroscopic properties. In this exercise, Dewar's MOPAC[15] PM6[23] MO method, and Pople's Gaussian[16] density functional theory (DFT)[17] method were used to to conduct energy minimisation and geometry optimisation, calculate molecular orbitals and derive the infra red spectral of molecules. This information is utilised to deduce and explain selectivity in reactions.

Regioselective Addition of Dichlorocarbene

Orbital Control of Reactivity

In the reaction of 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene 12 with dichlorocarbene, Halton et al observed high π-regioselectivity, with the only syn-monoadduct observed[24] (i.e. addition across the C=C bond on the same side as the Cl).

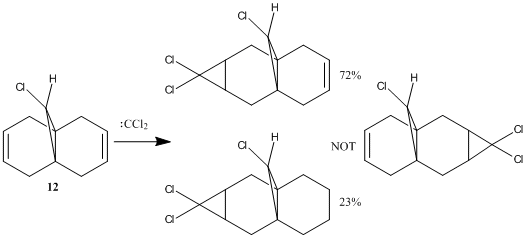
The energy and shape of the molecular orbitals (MO) of 12 are computed to determine the electronic structure of the molecule. As the orbitals with energies close to the HOMO (highest occupied MO) and LUMO (lowest unoccupied MO) control the reactivity of a molecule, the regioselectivity of the electrophilic addition reaction between 12 and dichlorocarbene, as shown on the right, can be explained by the MO diagrams shown below.

Table 4: Molecular Orbitals of 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene 12
HOMO-1

HOMO

LUMO

LUMO+1

LUMO+2

Examination of the HOMO shows that there is higher electron density at the syn-alkene than at the anti-alkene, so the syn-alkene is more nucleophilic. Since the reaction with dichlorocarbene is an electrophilic addition, it follows that electrophile will attack the electon rich syn-alkene rather than the electron poor anti-alkene. In contrast, the HOMO-1 has higher electron density at the anti-alkene. This findings are supported by MO calculations by Rzepa et al[25] using the PM3 method for MOPAC calculation, with some differences due to the variation of methods and conformations of the diene.

Rzepa et al[25] attributed the lower energy of the anti-alkene to stabilising antiperiplanar interactions between the C-Cl σ* orbital (LUMO+1 here, but LUMO+2 in reference[25]) and the occupied anti-alkene π orbital (HOMO-1). This results in the anti-alkene π orbital being stabilised with respect to the syn-alkene π orbital (HOMO). The build-up of electon density on the syn-alkene is also a result of the larger sterically accessible π orbital area at the syn-alkene, thus making it more susceptible to electrophilic attack.

From MO theory, the LUMO and LUMO+1 orbitals are expected to be π* orbitals, and Rzepa et al reported that the LUMO+2 is the C-Cl σ* orbital[25]. However, the results obtained in this exercise showed LUMO and LUMO+2 orbitals to be π* orbitals, and the LUMO+1 orbital to be the C-Cl σ* orbital. This discrepancy can be attributed to the flat conformation of the molecule obtained in this exercise versus the puckered version reported by Rzepa et al[25], which results in increased symmetry. Hence, orbital mixing between the anti-alkene orbital, the C-Cl σ* orbital and another higher energy σ* orbital can occur to stabilise both the 'anti-alkene orbital and the C-Cl σ* orbital, thus lowering the energy of both orbitals with respect to the other π and π* orbitals respectively.

Vibrational Frequencies

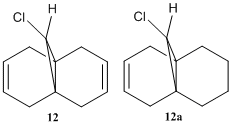
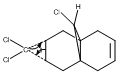
To study the influence of the C-Cl bond on the vibrational frequencies of 12, a comparison of the C-Cl and C=C stretching frequencies was made between molecule 12 amd its mono-hydrogenated derivative 12a in which the anti-alkene has been hydrogenated, as shown on the right.

Table 5: Infra Red Stretching Frequencies
Molecule C-Cl stretch /cm-1 syn C=C stretch /cm-1 anti C=C stretch /cm-1
Diene 12

DOI:10042/to-2483

770.9 1757.3 1736.9
Alkene 12a

DOI:10042/to-2482

775.0 1758.1 -

The stretching frequencies of the C-Cl bonds in both molecules correspond to the literature value for C-Cl at 780 cm-1[26]. The C=C stretching frequencies reported are, however, significantly higher than the literature value of 1620-1680 cm-1[27]. For the anti-alkene, this can be attributed to the stabilisation of the π orbital due to mixing with the σ* orbital of the C-Cl bond.

Comparing the IR of the syn- and anti- alkenes in diene 12, the syn-alkene has a higher stretching frequency, indicating a higher bond energy. This is in contrast with the molecular orbital discussion above which indicates that the syn-alkene is more reactive. This discrepancy results because the strength of the C=C bond depends on both the σ and π bond, while electrophilic addition reactions only attack the π bond. A σ effect of the C-Cl bond on the alkenes is the inductive withdrawal of electron density from the σ bond of the anti-alkene, thus making it weaker than the syn-alkene.

There is little difference between the stretching frequency of the syn-alkene in both the diene and the alkene, indicating that the anti-alkene does not affect the strength C=C bond of the syn-alkene in the diene.

Substitutents on the Anti-Alkene

To further study the effect of substituents on the stretching frequencies of diene 12, substituents with differente electronic properties were added to the anti-alkene.

The table below lists the stretching frequencies of the C-Cl and C=C bonds of the substituted dienes, with substituents in order from the most electropositive to the most electronegative groups.

Table 6: IR Stretching Frequencies of Substituted 12
Molecule Group C-Cl stretch /cm-1 syn C=C stretch /cm-1 anti C=C stretch /cm-1
12b SiH3 763.8 1756.3 1690.3
12c OH 765.3 1753.0, 1757.7 1753.0, 1757.7
12d CN 765.8 1756.5 1706.3

Comparing tables 5 and 6, it can be on deduced that substituents on the anti-alkene decrease the stretching frequencies of the C-Cl and both C=C bonds, indicating a decrease in bond energy. This effect is greatest at the anti-alkene, where the substituents are located. Thus it can be concluded that substitution at the anti-alkene makes weakens the bonds of the diene.

The more electropositive substituents decrease the stretching frequencies to a greater extent. This indicates that an increase in electron density in the diene destabilises molecules and weakens the bonds.

The OH group is inductively electron-withdrawing, but donates electrons by resonance. The addition of this substituent results in the two alkenes having the same two C=C stretching frequencies.

Structure-Based Mini Project

This mini-project is based on isomerism in 5-Benzotriazolyl-1-[(1S)-phenylethyl]-pyrrolidin-2-one, and utilises experimental data from Katritzky et al in their paper entitled[28].

The aim of this project is to use computational calculations of molecular properties, especially 13C NMR, to analyse the experimental data on 5-Benzotriazolyl-1-[(1S)-phenylethyl]-pyrrolidin-2-one isomers and attempt to characterise the isomers.

Isomerism in 5-Benzotriazolyl-1-[(1S)-phenylethyl]-pyrrolidin-2-one

In the novel synthesis of 1,5-disubstituted pyrrolidin-2-ones[28] via benzotriazole strategy[29], Katritzky et al reported the preparation of intermediate 5-Benzotriazolyl-1-[(1S)-phenylethyl]-pyrrolidin-2-one.

The reaction of 2,5-dimethoxy-2,5-dihydrofuran with benzotriazole and 1-phenylethylamine gave regioisomers 5-(benzotriazol-1-yl)-1-[(1S)-phenylethyl]-pyrrolidin-2-one 9h (67%) and 5-(benzotriazol-2-yl)-1-[(1S)-phenylethyl]-pyrrolidin-2-one 10h (15%), along with a minor by-product 1-(1-[(1S)-phenylethyl]-1H-pyrrol-2-yl)-1H-1,2,3-benzotriazole 11 (2%), as shown in the reaction mechanism below. Despite the use of chiral reagent 1S-phenylethylamine, there was little chiral control at the 5-position, and diastereomeric mixtures were obtained for both intermediates 9h (57:43) and 10h (53:47)[28].

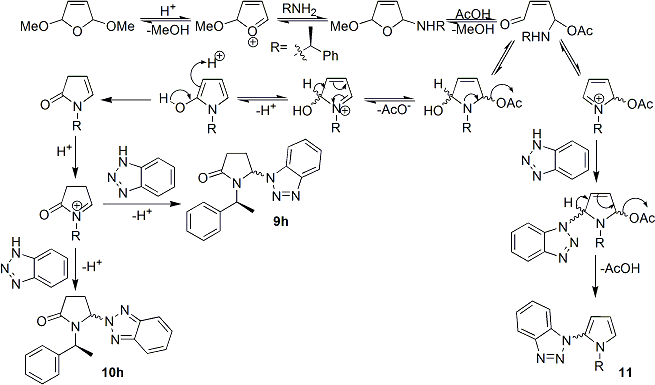
Data reported for both 9h and 10h is shown below[28]:

5-(1H-1,2,3-Benzotriazol-1-yl)-1-[(1S)-1-phenylethyl]-pyrrolidin-2-one (9h). Obtained as diastereoisomers in theratio 57:43 (minor isomer in the parentheses): yellow oil; 1H NMR δ 0.79 (d, J ) 7.2 Hz, 3H), 2.26-2.38 (m, 1H), 2.53-2.77 (m, 2H), 3.12-3.30 (m, 1H), 5.50-5.65 (m, 1H), 6.05-6.15 (m, 1H), 7.03 (d, J ) 8.0 Hz, 1H), 7.15-7.25 (m, 2H), 7.30-7.53 (m, 5H), 8.10 (d, J ) 7.6 Hz, 1H); 13C NMR δ 15.8 15.1), 26.8 (27.0), 29.7 (29.4), 50.2 (50.5), 69.9 (69.6), 109.3(109.1), 120.4 (120.1), 124.3 (124.2), 127.6 (127.5), 127.8 (127.6), 128.2 (127.9), 128.9, 131.3, 138.5, 146.1 (147.2), 174.9(175.2). Anal. Calcd for C18H18N4O: C, 70.57; H, 5.92; N, 18.29. Found: C, 70.23; H, 6.02; N, 18.46.

5-(2H-1,2,3-Benzotriazol-2-yl)-1-[(1S)-1-phenylethyl]-pyrrolidin-2-one (10h). Obtained as diastereoisomers in the ratio 53:47 (minor isomer in the parentheses): yellow oil; 1H NMR δ 0.79 (d, J ) 7.2 Hz, 3H), 2.13-2.28 (m, 1H), 2.37-2.63 (m, 2H), 3.15-3.35 (m, 1H), 5.52-5.65 (m, 1H), 6.09-6.15 (m, 1H), 7.25-7.51 (m, 7H), 7.83-7.95 (m, 2H); 13C NMR δ 15.3 (14.6), 27.3 (27.1), 29.1 (28.6), 50.1 (50.8), 76.5 (76.1), 118.3 (118.2), 126.7 (126.5), 127.4 (127.2), 127.9, 128.7, 138.9, 144.2 (144.7), 175.3 (175.0).

The table below shows the isomers of 5-(Benzotriazolyl)-1-[(1S)-1-phenylethyl]-pyrrolidin-2-one.

Table 7: Isomers of 5-Benzotriazolyl-1-[(1S)-phenylethyl]-pyrrolidin-2-one
5-(Benzotriazol-1-yl)-1-[(1S)-1-phenylethyl]-pyrrolidin-2-one 9hA
9hA

DOI:10042/to-2508

5-(Benzotriazol-1-yl)-1-[(1S)-1-phenylethyl]-pyrrolidin-2-one 9hB
9hB

DOI:10042/to-2485

5-(Benzotriazol-2-yl)-1-[(1S)-1-phenylethyl]-pyrrolidin-2-one 10hA
10hA

DOI:10042/to-2509

5-(Benzotriazol-2-yl)-1-[(1S)-1-phenylethyl]-pyrrolidin-2-one 10hB
10hB

DOI:10042/to-2507

Computational Calculation of 13C NMR for 5-Benzotriazolyl-1-[(1S)-phenylethyl]-pyrrolidin-2-one Isomers

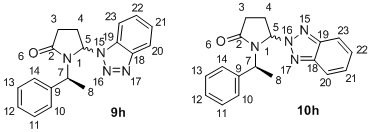
The 13C NMR of 9h and 10h reported by Katritzky indicates the signals belonging to the major and minor diastereomers of each intermediate. However, it neither assigns the signals to the specific conformation, nor to the individual carbon atoms. Hence, this mini-project aims to complete the assignment of 13C NMR. The diagram on the right shows the numbering of atoms, so the chemical shifts can be assigned to their respective C atoms.

13C NMR was predicted using the Gauge Invariant Molecular Orbital (GIAO)[30] approach with Gaussian[16] density functional theory (DFT)[17]. The method used was mPW1PW91, and the solvent CDCl3. Results obtained are shown below.

Computationally Calculated 13C NMR for Diastereomers

Table 8: 13C NMR Chemical Shift for Diastereomers
Carbon 9hA Shift / ppm 9hB Shift / ppm 10hA Calc. Shift / ppm 10hB Calc. Shift / ppm
8 16.2 15.7 16.4 15.5
4 27.2 25.9 29.8 29.8
3 31.2 31.3 30.1 31.1
7 51.8 50.2 51.6 49.5
5 71.6 71.7 76.3 76.0
23 107.3 107.0 116.4 (d=2) 115.8
20 118.9 118.2 116.3 (d=2) 116.1
21 121.2 120.6 123.8 123.5
10 124.2 120.3 123.7 120.5
12 125.0 (d=2) 123.1 124.6 122.9
11 125.0 (d=2) 123.7 124.7 122.8
22 125.4 124.5 124.0 123.4
13 126.0 124.6 125.5 124.1
14 126.9 126.5 126.9 126.7
19 127.1 126.2 141.2 138.6
9 137.6 137.6 134.8 136.6
18 145.7 143.1 139.2 140.6
2 167.6 167.7 168.2 169.6

Note: All chemical shifts are non-degenerate except for those labelled d=2, for which degeneracy is 2.

Discerning Isomers via GIAO 13C NMR Predictions

The GIAO calculation of 13C NMR can easily distinguish between regioisomers 9h and 10h, especially:

C-5, has chemical shift δ = 71.6 ppm for 9h and δ = 76.0 ppm for 10h.

C-23 has chemical shift δ = 108.3 ppm for 9h and δ = 116.0 ppm for 10h.

C-19 has chemical shift δ = 126.7 ppm for 9h and δ = 139.9 ppm for 10h.

For diastereomers, the difference in chemical shifts is smaller than the error in calculated chemical shifts. Sarotti et al showed that using mPW1PW91/6-31G(d) method with TMS as the standard, the mean-absolute-difference (MAD) error for the chemical shifts of sp3-hybridised carbon atoms is 1.4 ppm and that for sp2-hybridised carbon atoms is 5.1 ppm[31].

The only observable difference between the two diastereomeric pairs is the existence of degeneracy in the isomers where the benzotriazoloyl group is pointing out of the plane i.e. 9hA and 10hA. In 9hA, the degeneracy is at C-11 and C-12, which does not occur in 9hB. In 10hA, the degeneracy occurs at C-20 and C-23, but is not visible for 10hB.

Hence, 13C NMR can be used to discern regioisomers but is not a viable method for distinguishing between diastereomers.

Correlating GIAO 13C NMR Predictions with Experimental Data

The GIAO[31] calculations cannot be completely correlated to the experimental data, mainly because the 13C NMR reported by Katritzky et al[28] is incomplete, and many aromatic carbons are missing.

However, there is sufficient data for the GIAO[31] calculations to support the assignment of regioisomers by Katritzky et al[28]:

C-5, has experimental chemical shift δ = 69.9 ppm (computational δ = 71.6 ppm) for 9h and experimental chemical shift δ = 76.3 ppm (computational δ = 76.0 ppm) for 10h.

C-23 has experimental chemical shift δ = 109.2 ppm (computational δ = 108.3 ppm) for 9h and experimental chemical shift δ = 118.3 ppm (computational δ = 116.0 ppm)for 10h.

For diastereomer assignment, the experimental 13C NMR data between diastereomers are too similar to be accurately matched to the computationally predicted chemical shifts. This is in addition to the fact that the GIAO[31] calculations cannot distinguish between diastereomers as the difference in their chemical shifts is smaller than the error margin.

Thus the stereochemistry of the diastereomers cannot be assigned, and the major and minor diastereromers cannot be identified.

Other methods, discussed below, will have to be employed to separate and assign the stereochemistry to the diastereomers.

Computational Calculation of Optical Rotation for 5-Benzotriazolyl-1-[(1S)-phenylethyl]-pyrrolidin-2-one Isomers

Optical rotation can be utilised to distinguish between diastereomers. As the is no experimental optical rotation values for the diastereomeric paris in literature, the molecules were submitted to the Chemistry SCAN to determine their optical rotation using Gaussian.

The optical rotation for molecules 9hA and 10hA were submitted twice, but could not be calculated by SCAN, and convergence failure occurred, with the run being terminated.

For molecules 9hB and 10hB, the table below shows the predicted optical rotations in CDCl3 at 589 nm:

Table 9: Optical Rotation of Isomers
Molecule Optical Rotation [α] / o
Isomer 9hB DOI:10042/to-2544 110.3
Isomer 10hB DOI:10042/to-2543 -169.2

Optical rotation can be used to identify isomers 9hB and 10hB. However, as the optical rotation for molecules 9hA and 9hB cannot be obtained, this method cannot be utilised to distinguish between the diastereomers.

Further Work-Up and Analysis Techniques

Katritzky et al reported the separation of regioisomers 9h and 10h by flash column chromatography with hexanes-EtOAc (7:3)[28], with 1H and 13C NMR data analysis. However, separation of the diastereomer pairs 9hA and 9hB, as well as 10hA and 10hA was not conducted, and 13C NMR data of the each pair of diastereomers was reported together. This section aims to investigate techniques for separation and analysis of the diastereomers.

Separation of Diastereomers

Unlike enantiomers, diastereomers can be easily separated by chromatography.

Preparative thin layer chromatography (TLC)[32] can be utilised for small-scale separation of the diastereomeric mixtures, since the compounds on the developed plate can be observed under ultraviolet (UV) light due to the aromatic phenyl and benzotriazolyl groups.

Flash Column Chromatography[33], both in manual and automated form, is useful for larger-scale separations, and again the compounds can be visualised by TLC under UV light.

For high resolution separations, High performance liquid chromatography (HPLC)[34] can be utilised.

Analysis of Diastereomers

As highlighted above, 13C NMR is insufficient to provide a definitive assignment of diastereomers. This section will discuss further methods to characterise and assign the diastereomers.

2D NMR[35] can be utilised to characterise pure samples of diastereomers and thus assign the stereochemistry to the products.

Nuclear Overhauser effect spectroscopy (NOESY)[36] is capable of establishing correlations between atoms which are spatially close via through-space coupling, but only for a single isotope. NOESY can be used to determine the stereochemistry of the diastereomers since there is a spatial relationship between the benzotriazolyl group and the 1S-phenylethyl substituent on the Nitrogen atom of pyrrolidin-2-one.

Heteronuclear Single Quantum Coherence (HSQC)[36], the correlation of proton with heteronuclear NMR such as 13C or 15N, is also useful in differentiating between the diastereomers of 9h and 10h since correlation between protons and Carbon or Nitrogen atoms can be utilised to elucidate the structure of the molecule.

Selectivity in Nucleophlic Attack of Benzotriazole

Regioselectivity of Benzotriazolyl Group

From the ratio of regioisomers 5-(benzotriazol-1-yl)-1-[(1S)-phenylethyl]-pyrrolidin-2-one 9h (67%) and 5-(benzotriazol-2-yl)-1-[(1S)-phenylethyl]-pyrrolidin-2-one 10h (15%) obtained, it is observed that there is some regioselectivity in the nucleophilic attack of benzotriazole on the N-[(1S)-phenylethyl]-1,3-dihydro-pyrrol-2-one intermediate.

Benzotriazole exists in two tautomeric forms, 1H-benzotriazole and 2H-benzotriazole, as shown on the right. Experimental data indicates that 1H-benzotriazole is the only stable tautomer in solid state, and that in gas phase spectroscopy 1H-benzotriazole is more stable than 2H-benzotriazole by 5 kJ mol-1[37]. Computational studies by Novak et al[38] have also shown that 1H-benzotriazole is the more stable tautomer by 1.1 kJ mol-1 in gas phase. The existence of 1H-benzotriazole as its hydrogen-bonded dimer or in higher agglomerates[29], as well as intermolecular hydrogen bonding, also accounts for 9h being the major regioisomer.

Stereoselectivity at 5-position of Pyrrolidin-2-one Ring

There was little chiral control at the 5-position of the pyrrolidin-2-one ring despite the use of chiral reagent 1S-phenylethylamine, and diastereomeric mixtures were obtained for both 9h (57:43) and 10h (53:47)[28]. Even so, the diastereomeric ratio indicates that there is a favoured product for each regioisomer.

This section aims to use Allinger's MM2[1] force field to determine the energies of the diastereomers and thus assign the products to specific isomers.

Table 10: Energies of Isomers
Diastereomer Energy / kJ mol-1
Molecule 9hA 91.2
Molecule 9hB 79.1
Molecule 10hA 92.6
Molecule 10hB 85.6

Comparing the energies of 9h diastereomers, 9hB has a lower energy and thus it is expected to be the major product. Similarly, 10hB has the lower energy of the two 10h diastereomers, and is also expected to be found in greater yield. This observation indicates that thermodynamically a higher proportion of nucleophilic attack from the bottom of the plane of the pyrrolidin-2-one ring occurs.

However, kinetically it is difficult for the nucleophilic attack to occur from the same plane of the pyrrolidin-2-one ring as the phenyl ring due to steric hindrance. Hence, there is little chiral control at the 5-position of the molecule.

Conclusion

The computational methods used in this mini project were only able to distinguish between regioisomers 9h and 10h, but were unable to differentiate between the diastereomeric pairs 9hA and 9hB, as well as 10hA and 10hB. Methods of separation and characterisation of the diastereomers have been suggested, and experimental data will have to be obtained and analysed to determine if these methods are viable.

References

  1. ↑ 1.0 1.1 1.2 N.L.J. Allinger, CJ. Am. Chem. Soc., 1977, 99, 8127: DOI:10.1021/ja00467a001
  2. ↑ P.J. Jr. Wilson, J.H. Wells, Chem. Rev., 1944, 34, 1: DOI:10.1021/cr60107a001
  3. ↑ 3.0 3.1 J. Sauer, R. Sustmann, Angew. Chem, 1980, 19, 779: DOI:10.1002/anie.198007791
  4. ↑ W.C. Herndon, C.R. Grayson, J.M. Manion, J. Am. Chem. Soc.., 2002, 124, 1130: DOI:10.1021/jo01278a003
  5. ↑ P. Caramella, P. Quadrelli, L. Toma, Chem. Rev., 1944, 34, 1: DOI:10.1021/ja016622h
  6. ↑ K. Alder, G. Stein, Angew. Chem, 1937, 50, 514: DOI:10.1002/ange.19370502804
  7. ↑ R. Hoffmann, R.B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388: DOI:10.1021/ja00947a033
  8. ↑ D. Skála, J. Hanika, Pet. Coal, 2003, 45, 105: PDF
  9. ↑ 9.0 9.1 J.J. Zou, X. Zhang, J. Kong, L. Wang, Fuel, 2008, 87, 3655: DOI:10.1016/j.fuel.2008.07.006
  10. ↑ Kirk-Othmer: Encyclopedia of Chemical Technology, 2nd Ed., Vol 6, p.688, John Wiley and Sons, 1985
  11. ↑ 11.0 11.1 Y.H. Lai, Synthesis, 1981, 1981, 585: DOI:10.1055/s-1981-29537
  12. ↑ 12.0 12.1 A.G. Shultz, L. Flood, J.P. Springer, J. Org. Chem., 1986, 51, 838: DOI:10.1021/jo00356a016
  13. ↑ 13.0 13.1 Jmol: an open-source Java viewer for chemical structures in 3D: http://www.jmol.org/
  14. ↑ 14.0 14.1 S. Leleu, C. Papamicaël, F. Marsais, G. Dupas, V. Leavacher, Tetrahedron: Asymmetry, 2004, 15, 3919: DOI:10.1016/j.tetasy.2004.11.004
  15. ↑ 15.0 15.1 MOPAC2009, J.J.P. Stewart, Stewart Computational Chemistry, Colorado Springs, USA, 2008: web
  16. ↑ 16.0 16.1 16.2 16.3 Gaussian 09, Revision A.1, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009: web
  17. ↑ 17.0 17.1 17.2 JP. Hohenberg, W. Kohn, Phys. Rev., 1964, 136, B864: DOI:10.1103/PhysRev.136.B864
  18. ↑ K.C. Nicolaou, P.G. Nantermet, H. Ueno, R.K. Guy, E.A. Couladouros, E.J. Sorensen, J. Am. Chem. Soc., 1995, 117, 624: DOI:10.1021/ja00107a006
  19. ↑ 19.0 19.1 19.2 19.3 W.F. Maier, P.v.R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891: DOI:10.1021/ja00398a003
  20. ↑ G. Bringmann, A.J.P. Mortimer, P.A. Keller, M.J. Gresser, J. Garner, M. Breuning, Angew. Chem. Int. Ed., 2005, 44, 5384: DOI:10.1002/anie.200462661
  21. ↑ 21.0 21.1 S.W. Elmore, L.A. Paquette, Tetrahedron Lett., 1991, 32, 319: DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
  22. ↑ J.R. Wiseman, W.A. Pletcher, J. Am. Chem. Soc., 1970, 92, 956: DOI:10.1021/ja00707a035
  23. ↑ J.J.P. Stewart, J. Mol. Modeling, 2007, 13, 1173: DOI:10.1007/s00894-007-0233-4
  24. ↑ B. Halton, S.G.G. Russell, J. Org. Chem., 1991, 56, 5553: DOI:10.1021/jo00019a015
  25. ↑ 25.0 25.1 25.2 25.3 25.4 B. Halton, R. Boese, H.S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
  26. ↑ G. Socrates, Infrared and Raman Characteristic Group Frequencies, 3rd Edition, 2001, p. 65.
  27. ↑ J. Coates, “Interpretation of Infrared Spectra, A Practical Approach", Encyclopedia of Analytical Chemistry, John Wiley & Sons Ltd, Chichester, 2000
  28. ↑ 28.0 28.1 28.2 28.3 28.4 28.5 28.6 28.7 "Preparation of 1,5-Disubstituted Pyrrolidin-2-ones" A.R. Katritzky, S. Mehta, H.Y. He, X. Cui, J. Org. Chem., 2000, 65, 4364: DOI:10.1021/jo000219w
  29. ↑ 29.0 29.1 A.R. Katritzky, X. Lan, J.Z. Yang, O. Denisko, Chem. Rev., 1998, 98, 409: DOI:10.1021/cr941170v
  30. ↑ R. Ditchfield, J. Chem. Phys., 1972, 56, 5688: DOI:10.1063/1.1677088
  31. ↑ 31.0 31.1 31.2 31.3 A.M. Sarotti, S.C. Pellegrinet, J. Org. Chem., 2009, 74, 7255:DOI:10.1021/jo901234h
  32. ↑ E. Soczewinski, T.Wawrzynowicz, "Preparative TLC", Encyclopedia of Chromatography, Taylor & Francis, 2005, pp. 1355:DOI:10.1081/E-ECHR-120040097
  33. ↑ W.C. Still, M. Kahn, A. Mitra, J. Org. Chem., 1978, 43, 2923:DOI:10.1021/jo00408a041
  34. ↑ L.R. Snyder, J.W. W. Dolan, High-Performance Gradient Elution: The Practical Application of the Linear-Solvent-Strength Model, Wiley Interscience, 2006, ISBN 0471706469
  35. ↑ K. Wüthrich, NMR of Proteins and Nucleic Acids., John Wiley and Sons: New York, Chichester, Brisbane, Toronto, Singapore, 1986
  36. ↑ 36.0 36.1 S. Talluri, G. Wagner, J. Magn. Reson., Ser. A, 1996, 112, 200:DOI:10.1006/jmrb.1996.0132
  37. ↑ W. Roth, D. Spangenberg, Ch. Janzen, A. Westphal, M. Schmitt, Chem. Phys., 1999, 248, 17: DOI:10.1016/S0301-0104(99)00262-1
  38. ↑ I. Novak, T. Abu-Izneid, B. Kovač, l. Klasinc, J. Phys. Chem. A., 2009, 113, 9751: DOI:10.1021/jp905640b
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod1:sherwingoh&oldid=815427"