Rep:Mod1:rastaeatinpasta

Module 1: The Basic Techniques of Molecular Mechanics and Semi-Empirical Molecular Orbital Methods for Structural and Spectroscopic Evaluations

Thomas Waugh

Computational Chemistry Lab Module 1

Introduction and Aims

During this project I will demonstrate how computers can be utilised to precisely model aspects of structure and reactivity of certain organic molecules. These techniques an be used to not only predict the most likely outcome of a reaction but can also be used to identify potentially useful adaptations or even new reactions. Molecular mechanics or (MM) is a relatively quick method for calculating the energy and other properties of the molecules. It achieves this by optimising the geometry to obtain an energy minimum. Rather than calculating the energy by solving wave equations quantum mechanically the energy is assumed to consist of the summation of all the diatomic bond stretches, triatomic bond angle deformations, tetra-atomic bond torsions, non-bonded Van der Waals attractions and repulsions and finally the sum of all electrostatic attractions of individual bond dipoles.

However the molecular mechanics approach does have its limitations, most notably since it is a parametric method, and uses data from well characterised and known molecules it is very difficult to accurately model new molecules or molecules with unusual bonding as the electron distribution has to be taken into account. During this project both the Allinger MM2 and MMFF94 approximation methods will be utilised.

Modelling using Molecular Mechanics

Hydrogenation of Cyclopentadiene Dimer

Dimerisation of Cyclopentadiene

Cylcopentadiene dimerises via a [π4s+π2s] cycloaddition Diels-Alder reaction. The dimerisation occurs to produce only the endo dimer 2 as opposed to the exo dimer 1.

Cyclopentadiene 4+2 cycloaddition Diels-Alder

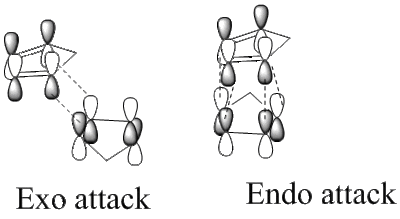
The stereo-specificity displayed in the reaction can be better understood via comparison of the relative energies of the dimers 1 and 2. this was carried out using ChemBio 3D, initially the molecule was drawn out with its approximate stereochemistry, then the MM2 force field option was used to optimise the geometry to give the lowest energy. The product with the lowest relative energy will be more thermodynamically stable but not necessarily the dominant product.

Energies for Cyclopentadiene Dimers

Molecule	Energy kcal/mol	Energy kJ/mol
exo dimer 1	31.88	133.41
endo dimer 2	34.00	142.29

As the table shows the exo product 1 (133.41 kJ mol^-1) is 8.88 kJ mol^-1 more stable than the endo product 2 (142.29 kJmol^-1). Therefore the exo product 1 is the more thermodynamically favoured product in the reaction. However it is known that when the reaction proceeds at room temperature it is the endo product 2 that dominates. This is due to the fact the reaction is under kinetic control since it is carried out at a fairly low temperature and the Diels-Alder reaction is effectively irreversible. Therefore the transition state with the lowest energy barrier will be the more favoured pathway hence the kinetic product (endo dimer 2) forms. The transition state for the endo product is slightly lower in energy than the exo product as it is stabilised by a secondary orbital interaction from the interaction of the p_z orbitals on the uninvolved double bond and the double bond being formed in the cycloaddition. Unfortunately the molecular mechanics approach being used does not allow the calculation of the energy of the transition states as it cannot take into account the sort of interactions described in the bond breaking/forming of the transition state. The endo-selectivity seen in this reaction can be confirmed via consideration of Alder's endo rule .

Hydrogenation of Cyclopentadiene dimer

The endo dimer 2 can be partially hydrogenated to give either products 3 or 4. To obtain the terahydro derivative further reaction with hydrogen in the presence of a catalyst is required.

Dihydro derivatives 3 and 4

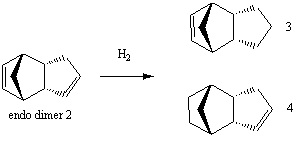
Again the molecules were drawn in ChemBio3D and their geometries were optimised using the MM2 force field option. This time the total energy was broken down into its energy contributions from stretching, bending, torsion etc.

Energy contributions for the products of the hydrogentaion of the endo isomer

	Energy kcal/mol
Energy Contribution	Product 3	Product 4
Stretch	1.27	1.10
Bend	19.81	14.51
Stretch-Bend	-0.83	-0.55
Torsion	10.87	12.51
Non-1, 4 VDW	-1.22	-1.10
1, 4 VDW	5.64	4.51
Dipole/Dipole	0.16	0.14
Total Energy	35.70	31.17

As it can be seen from the table above the dihydro derivative product 4 had the lowest total energy (4.53 kcal mol^-1 more stable) and as a result is the thermodynamically favoured product. This implies that the double bond in the six membered ring is more likely to be hydrogenated before the double bond in the 5 memebered ring. This is in agreement with the literature which states that the carbon carbon double bond in the norbornene moiety is hydrogenated prior to the double bond in the 5 membered ring.

The origin of this difference in energy can be traced back to the two molecules respective differences in their bending energy contributions. The bending energy of product 3 is 5.3kcal mol^-1 larger than in the expected product 4. This can be better rationalised by using ChemBio3D to calculate how strained the C=C bond angles are in the respective products. How strained the bonds are will depend how far they deviate from the idealised bond angle of a typical sp² centre (120^o). It was determined that the bond angle of the C=C double bond in the six memebered ring of product 3 was 107.8^o indicating the bond angle is very highly strained in comparison to the bond angle measured for product 4 (112.8^o). This still deviates quite significantly from 120^o but explains why product 3 is higher in energy and consequently less stable.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD⁺ analogue)

The Reaction of N-Methyl Pyridoxazepinone with Methyl Magnesium Iodide

Reactant 5 (N-methyl pyridoxazepinone) is an optically active derivative of prolinol and can react with a Grignard reagent (methyl magnesium iodide) to alkylate the pyridine ring at the 4-position. The reaction proceeds with the absolute stereochemistry seen in the product 6.

Reaction of N-Methyl Pyridoxazepinone with Methyl Magnesium Iodide

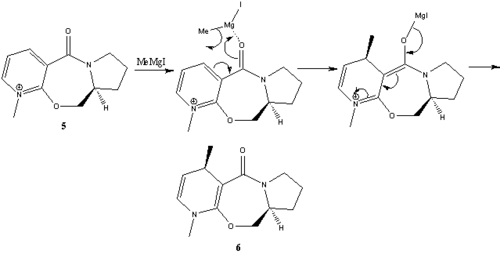
Both the stereo- and regio selectivity observed in the reaction can be understood by examining the interaction between the two reactants. As suggested in the literature by Schultz et al the electropositive magnesium atom of the Grignard reagent bonds to the electronegative oxygen atom of the carbonyl on the cyclic amide ring moiety. The coordination is then followed by the a nucleophilic attack of the methyl group at the 4-position on the pyridinium ring. The attack of the methyl group will occur on the same face that the magnesium is coordinated to the oxygen atom, therefore the geometry of the carbonyl group with respect to the aromatic ring will determine the stereochemistry of the incoming nucleophile. The geometry of the N-Methyl Pyridoxazepinone was optimised again using the MM2 approximation method, the dihedral angle between the oxygen atom of the carbonyl group and the carbon atom at the 4-position of the pyridinium ring was measured. The dihedral angle was then varied to see how this effected the relative energies of the optimised geometries.

Energy against pyridinium ring/carbonyl dihedral angle- Molecule 5

Dihedral angle	Energy kcal mol-1
0o	48.38
5o	46.94
10o	45.86
15o	45.15
20o	44.78
21o	44.75
22o	44.73
23o	44.73
24o	44.74
25o	44.77
30o	45.05
35o	45.65

As it can be seen from the above table and graph the optimised dihedral angle was found to be 23.4^o giving a total energy of 44.68kcal mol^-1. Since the carbonyl group points "up" slightly with respect to the pyridinium ring the nucleophilic attack of the methyl group approaches from the top face hence the stereochemistry observed in product 6. The model below shows the optimised geometry which gave the lowest total energy for molecule 5, it should also be noted that the dihedral angle was varied to negative values (i.e. the carbonyl points down with respect to the pyridinium ring) however the minimised energy values were all much higher than in the previous conformations (>50 kcal mol^-1). Unfortunately MeMgI could not be included in the calculations as Mg is not recognised by MM2 as an error message is displayed saying "atom type" for Mg is not defined.

Optimised geometry of N-Methyl Pyridoxazepinone

Reaction of N-Methyl Quinolinium and Aniline

The reaction shown below of N-methyl quinolinium salt 7 and aniline is another example of a stereo- and regioselective reaction which can also be modelled to better visualise the geometry of the substituents and gain insight into the observed stereo and regioselectivity of the product 8.

Reaction of N-Methyl Quinolinium and Aniline

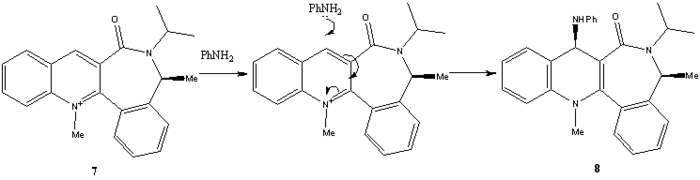
Again molecule 7 was modelled using ChemBio3D and the geometry was optimised to give the lowest energy conformation. The lowest enenrgy geometry can be seen below. As can be seen from the optimised geometry of molecule 7 the carbonyl group points downwards with respect to the planar pyridinium ring. Therefore the dihedral angle between the oxygen atom and the carbon atom at position 4 on the pyridinium ring was varied to optimise the total energy to find the lowest energy conformation.

Optimised energy against pyridinium ring/carbonyl dihedral angle

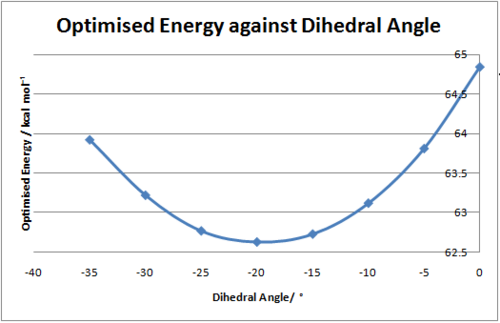
Dihedral Angle	Energy kcal mol-1
0o	64.84
-5o	63.81
-10o	63.12
-15o	62.73
-20o	62.63
-25o	62.77
-30o	63.22
-35o	63.91

The reaction mechanism is slightly different to the previous example because the nucleophile NPhH₂ doesn't coordinate to the oxygen lone pair of the carbonyl group. Although no coordination takes place this is not to say the carbonyl group and its associative geometry doesn't play an important role in determining the final stereochemistry of the product. Similarly like the previous example the nuclephilic addition occurs at the 4-position on the pyridinium ring as the is the only site of attack available.

The lowest energy geometry was found to have a total energy of 62.63 kcal mol^-1 whereby the dihedral angle was found to be -19.24^o, this clearly indicates that the carbonyl group points below the plane of the the pyridinium ring. As a result the incoming nucleophile would be expected to approach from the opposite face to the carbonyl to minimise the electrostatic repulsions of the nitrogen lone pair and the oxygen lone pairs on the carbonyl moiety. Thus the nucleophile will approach from the top face of the pyridinium ring and attack the 4-position to give the observed stereochemistry 8. The results obtained here are consistent with those found by Leleu et al who suggested the amine approaches the pyridinium ring from the opposite face to which the carbonyl is pointing. It should also be noted that the dihedral angle was varied to positive values (i.e. the carbonyl points above the plane of the pyridinium ring) however the optimised energies were higher than in the previous conformations (Dihedral angle = 20^o, Energy = 71.21 kcal mol^-1)this indicates that having the carbonyl pointing above the plane is disfavoured.

Optimised geometry of N-Methyl Quinolinium

Possible Improvements

To overcome the problem of not being able to model the magnesium atom an alternative method that can take into account more than one molecule could be used. Alternatively the MOPAC molecular orbital approach considers the electronic properties of a molecule e.g. the molecular orbitals involved in bonding. furthermore DFT calculations can estimate the energy variations as the Gignard interacts with the N-methyl pyridoxazepinone (molecule 5).

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

In the synthesis of Taxol the intermediates 9 and 10 are formed. At first both isomers are formed in which the carbonyl is either pointing up or down. The two isomers shown are examples of atropisomers ( these are stereoisomers brought about from restricted rotation about single bonds whereby the steric strain barrier to rotation is sufficiently large enough to allow separation of conformers). The rotation of the single bonds either side of the carbonyl group is restricted due to the high steric strain associated with the movement of the functionality. Over time it was discovered that molecule 9 isomerises to a single isomer (molecule 10).

Intermediates in the synthesis of Taxol

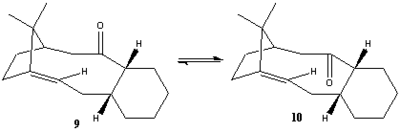
The lowest energy atropisomer was calculated using both the MM2 and MMFF4 approximation methods using ChemBio3D Ultra 12, the resulting energy contributions (MM2) are displayed below.

Energy Contributions for Intermediates 9 and 10

Energy contribution	Intermediate 9 (kcal mol-1)	Intermediate 10 (kcal mol-1)
Stretch	2.70	2.55
Bend	15.94	9.99
Stretch-bend	0.40	0.28
Torsion	18.26	19.39
Non-1,4 VDW	-1.22	-1.52
1,4 VDW	12.69	12.60
Dipole/dipole	0.14	-0.19
Total energy (MM2)	48.91	43.09
Total energy (MMFF94)	70.54	61.20
Structures

After consideration of both the stereochemistry in the reaction scheme and the literature it was concluded that both structures 9 and 10 could be wrong. For example in molecule 9 according to the literature proposed by Paquette et al the cyclohexane ring in molecule 9 should have the twisted boat conformation as opposed to the chair conformation as seen above. Although the structures in the literature were modified slightly with varying functional groups on the cyclohexane ring. It seems although not explicitly stated that structure 9 with the carbonyl pointing upwards should have the cyclohexane ring in the twist boat conformation, the modified energies and structure is shown below. As for structure 10 after the optimisation of the geometry to find the minimum in energy (MM2) it was assumed the observed energy was as expected because it was in agreement with the literature i.e. the energy for structure 10 should be lower in energy than structure 9 hence why 9 isomerises to 10 over time as it is the more thermodynamically stable product. this makes sense from the original energy calculations as in both the MM2 and MMFF94 calculations structure 10 was lower in energy than structure 9. However the stereochemistry shown above is not the same as depicted in the reaction scheme whereby the the two hydrogens attached to the cyclohexane ring are both pointing out of the plane and in the same direction whereas in the structure shown above they point in opposite directions. This was corrected by simply moving the atoms and re-optimising the geometry. I believe the final structure shown below does show the correct stereochemistry as the the hydrogen on the alkene is still cis to the gem-dimethyl bridge, the cyclohexane ring is in its lower energy chair conformation (this was in agreement with the literature) and the two hydrogen attached to the cycloheaxne ring both point in the same direction.

Corrected Energy Contributions for Intermediates 9 and 10

Energy contribution	Intermediate 9 (kcal mol-1)	Intermediate 10 (kcal mol-1)
Stretch	2.84	2.54
Bend	16.53	10.68
Stretch-bend	0.47	0.32
Torsion	21.25	19.77
Non-1,4 VDW	-0.91	-1.39
1,4 VDW	14.09	12.56
Dipole/dipole	0.14	-0.18
Total energy (MM2)	54.41	44.29
Total energy (MMFF94)	76.29	60.57
Structures

In both cases whether structure 9 adopts the higher energy twist boat conformation or the lower chair conformation (54.41 and 48.91 kcal mol^-1) the total energy is always higher than the energy of the structure 10 which adopts the chair conformation (44.29 kcal mol^-1). By far the most significant difference between the two structures is the contribution of the bending energy. In both the the twist boat and chair conformations of structure 9 the bending energy is substantially higher than in the chair conformation of structure 10 (16.53 and 15.94 kcal mol^-1 compared to 10.68 kcal mol^-1). It would be expected that structure 9 would take the chair conformation as it is lower in energy and thus more thermodynamically stable and since there are many structures known for cyclohexane (chair, boat, twist boat etc) it may be possible to obtain different conformations depending on the substituents. However the calculations here show that structure 10 is slightly more stable and explains why over time 9 isomerises to 10. The difference in bending energy could be attributed to the deviation of the sp² carbon atom from its idealised bond angle of 120^o, the further it deviates from this bond angle the higher the bending energy. For the twist boat conformations of intermediate 9 the bond angle was found to be 126^o this is quite a large deviation compared to the chair structure for 10 which has a bond angle of 118^o. Hence the geometry of the carbonyl (up or down relative to the ring) determines the conformation of the cyclohexane moiety and also explains why intermediate 10 is lower in energy and hence the most thermodynamically stable.

The total energy was also calculated using the MMFF94 force field option and in all cases the total energy was higher than in the MM2 option. However the energy calculations still show the same trend in that structure 10 is lower in energy than either the twist boat or chair conformations of structure 9.

Hyperstable Alkenes

The intermediate shown react much more slowly to hydrogenation than other strained alkenes due to the high stability of the bridgehead alkene. Hyperstable alkenes or olefins are said to have negative 'olefin-strain energy' (OSE) this is described as the difference in strain energy of the olefin and its parent hydrocarbon. Therefore hyperstable alkenes are less strained than their associated hydrocarbon and as a result show decreased reactivity. The hyperstable alkene arises due to the position of the bridgehead which in this case results in a twist in the double bond reducing the pi overlap (smaller HOMO-LUMO gap). The bridgehead carbon also increases the steric hindrance of the double bond to incoming attack again resulting in a much slower reactivity.

Modelling Using Semi-empirical Molecular Orbital Theory

There are many limitations of the molecular mechanics approach mainly its inability to take into account electrons within molecules. However the molecular orbital approach shows how electrons manipulate bonds and generate spectroscopic characteristics. In all the calculations the MM2 force field was used to optimise the geometry then minimised again using the MOPAC PM6 molecular orbital. approach.

Regioselective Addition of Dichlorocarbene

Orbital Control of Reactivity

The reaction of dichlorocarbene with molecule 11 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanoaphthalene was shown to be highly regioselective as observed by Halton et al. The reaction produced almost exclusively the endo product (mono-adduct 72%) from the addition across the syn alkene. The di-adduct adduct was also formed (23%) although the exo product was not observed. The rationale behind this can be better understood if the molecular orbtals involved are considered.

Reaction of Dichlorocarbene with molecule 11

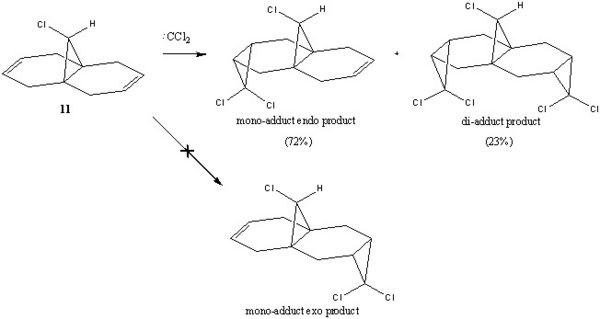
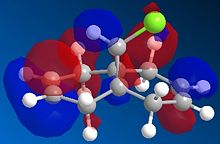
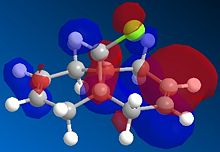
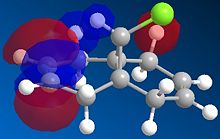
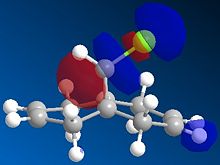
The regioselectivity of molecule 11's reactivity with the electrophile dichlorocarbene cannot be rationalised by considering the mechanical characteristics of the molecule as neither double bond is particularly strained or sterically hindered for electrophilic attack. Therefore the more nuclephilic double bond will determine where the addition occurs on the molecule. For this example the semi-empirical molecular orbital approach was used to model the molecular orbitals to gain a better understanding of the electron density in the frontier molecular orbitals. The molecules geometry wast first optimised using the MM2 force field followed by a further optimisation using the MOPAC/PM6 method. From the resulting optimisation the heat of formation was found to be 19.74 kcal mol^-1. The frontier molecular orbitals were as follows.

Frontier Molecular Orbitals for Molecule 11

HOMO-1 (N=31)	HOMO (N=32)	LUMO (N=33)	LUMO+1 (N=34)	LUMO+2(N=35)

The diagrams above clearly shows that the HOMO (highest occupied molecular orbital) has most of its electron density at the syn alkene this is the alkene on the same side as the chlorine atom. As a result the syn C=C double bond will most nuclephilic due to the fact it has the greatest degree of electron density. Therefore it is most likely to react with the electrophile giving the mono-adduct (the endo-product).

The HOMO-1 shows the majority of the electron density on the anti C=C double bond, since this orbital is lower in energy than the HOMO this explains the extra stability of the anti double bond and why the syn alkene reacts more readily. The anti double bond is also lower in energy due to an antiperiplanar interaction between the (σ*(C-Cl)) depicted in the LUMO+1 diagram and the occupied (π(C=C))shown in the HOMO-1 diagram. The resulting stabilisation lowers the energy of the anti alkene (by 0.08eV relative to the syn double bond) leading to its lower reactivity with electrophiles as proposed by Rzepa et al.

Vibrational Frequencies

The vibrational frequencies associated with molecule 11 notably the C-Cl stretch as well as the two C=C double bonds (syn and anti). The dialkene was compared to its hydrogenated form the mono-alkene (molecule 12 with the exo bond hydrogenated). The vibrations were calculated by using a density functional approach, this utilised the B3LYP/6-31G(d,p) Gaussian geometry optimisation and frequency analysis.

C-Cl and C=C stretching frequencies for molecule 11, 12 and their derivatives

Molecule	C-Cl/ cm-1	C=C (anti)/ cm-1	C=C (syn)/ cm-1	Structure
dialkene 11	770.81	1737.04	1757.44
monoalkene 12	774.96	N.A.	1758.06
=C-OH	766.78	1776.61	1756.24
=C-CN	765.77	1706.28	1756.54
=C-BH2	759.05	1657.20	1756.55
=C-SiH3	763.83	1690.35	1756.25

The stretching frequencies calculated for the C-Cl bond for each molecule were all in the region expected at ~770cm^-1. The IR spectrums for the dialkene (molecule 11) and the monoalkene (molecule 12) are quite similar, this is expected since most of the functional groups are present in both molecules. The main difference between 11 and 12 is that in the dialkene both the anti (1737.04cm^-1) and syn (1757.44cm^-1) C=C bonds are present whereas in the monoalkene only the syn (1758cm^-1) C=C bond was observed. It is important to note the calculated C=C stretching frequencies were higher (larger wavenumber) than the expected region for C=C bonds (1600-1700cm^-1). The reason for this may be partly due to the electron withdrawing nature of the Cl atom but it is more likely due to the fact stretching frequencies are systematically calculated too high so have to be corrected for by 8%. Also a larger wavenumber indicates a stronger bond, therefore the same rationale for the stabilisation of the anti double bond via the antiperiplanar interaction of the (σ*(C-Cl)) and the occupied (π(C=C)) can be applied. From molecule 11 it can be seen that the stretching frequency for the anti alkene (1737.04cm^-1) is lower than the syn alkene (1757.44cm^-1). This implies that the syn double bond is stronger than the anti which is the reverse of what the molecular orbitals suggest in terms of stability. The reason that the anti double bond is more stable than the syn double bond yet stretches at a lower frequency can be explained from consideration of the π electrons. In the anti double bond electrons are withdrawn towards the Cl partially forming the Cl anion. As a result of this the π electron density in the double bond decreases meaning the bond has more σ character and since σ electrons are lower in energy the bond is more stable but vibrates easier hence at a lower stretching frequency. Finally the reason the C-Cl stretching frequency of 11 (770.81cm^-1) was lower and hence weaker than 12 (774.96cm^-1)was due to the fact that the dialkene has the π(C=C) to σ*(C-Cl) donation, this weakens the C-Cl bond and hence it has a lower stretching frequency.

To take this further one of substituents on the anti alkene was modified to see what effect this had on the C-Cl and C=C stretching frequencies, their structures are also shown in the table. As it can be clearly seen from the table changing the substituent on the anti alkene has little effect on the C-Cl and syn C=C stretching frequencies. Upon the addition of a hydroxyl group to the anti alkene the bond strength increases (stretching frequency moves to a higher wavenumber relative to the dialkene). The reason for this is because the oxygen atom donates electron density via resonance to the π orbitals of the C=C bond, this resonance stabilises the bond meaning it has a higher stretching frequency. As for the addition of the cyano group it can be seen from the data that this addition weakens the bond (lower stretching frequency) due to the nitrogen atom which withdraws electron density away from C=C bond. By far the largest substituent effect seen is the addition of the BH₂ and SiH₃ groups, BH₂ acts like a lewis acid capable of accepting electron density from the π C=C bond into its unoccupied p orbitals. A similar effect was observed with the siyl group however the effect is not as dramatic since SiH₃ is less lewis basic since it accepts electron density into unoccupied more diffuse d-orbitals which are higher in energy. the result of both groups was to weaken the C=C bond hence the stretching frequency was at a lower wavenumber relative to the original dialkene.

Structure Based Mini Project

Most reactions give a mixture of products these can sometimes by regioisomeric, stereoisomeric etc. The most likely outcome of a reaction i.e. which product dominates can usually be understood from the mechanism, however since the mechanism cannot be observed the structure of the resulting product(s) needs to be carefully analysed. The analysis is usually best characterised by NMR spectroscopy (¹H or ¹³C to name a few). This project demonstrates how ¹³C NMR can be used to distinguish between two regioisomeric products as well as other techniques which can further predict the different spectroscopic properties including their short comings. All of the data included was calculated and that in its self demonstrates how powerful computational chemistry is as it allows the outcome of a reaction to be understood despite not entering a synthetic laboratory.

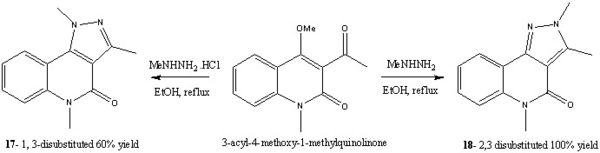
Introduction: Regioselective Cyclisation of 3-Acyl-4-Methoxy-1-Methylquinolinones with Hydrazines

Pyrazoles are heterocycles often found in many biological systems and have therefore found themselves at the core in many anticancer, antiviral, anti-inflammatory and antidepressant pharmaceuticals. Chimichi et al reported on the regioselective synthesis of 1,3-disubstituted- and 2,3-disubstituted-pyrazolo[4,3-c]quinolin-4(5H)ones, compounds 17 and 18 respectively. Both of the regioisomers were formed from the reaction between 3-acyl-4-methoxy-1-methylquinolinone and N-methylhydrazine under different reaction conditions. It was found that the reaction proceeded selectively and exclusively to give either the 1,3-disubstituted- or 2,3-disubstituted-pyrazolo[4,3-c]quinolin-4(5H)one depending on the reaction conditions.

Regioselective Cyclisation of 3-Acyl-4-Methoxy-1-Methylquinolinones withN-methylhydrazine

Mechanistic Analysis

Reaction mechanism for the formation of 17

Reaction mechanism for the formation of 18

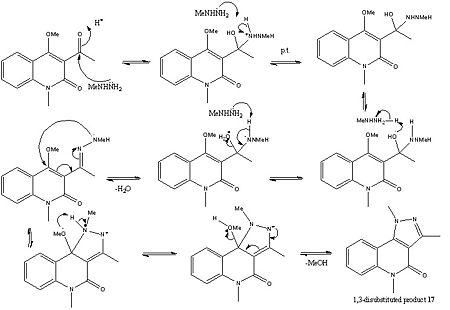
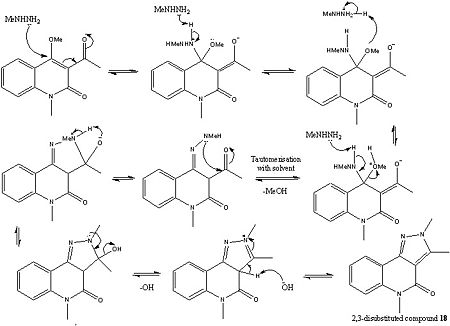
As it can be seen from above the pyrazole ring formation is strongly dependant upon the acidity of the solution, as this has a strong effect on governing the site of attack of the N-methylhydrazine. For example in an acidic medium i.e. when hydrazine hydrochlorides were used to form molecule 17 (1,3-disubstituted product), this was described in the literature as being the normal site of attack for the N-methylhydrazine. Although not explicitly stated in the literature this could be due to the fact the acidic conditions protonate the carbonyl and therefore make it more electrophilic. On the other hand when N-methyl hydazine free bases were used the 2,3-disubstituted product was obtained (molecule 18). In the literature this was attributed to the fact that the initial site of attack was at the 4-position on the pyridine like ring (carbon atom 10), in other literature by Sloop et al this was described as a Michael-fashion attack although in both pieces of literature neither explains why this attack happens over the addition to the carbonyl. Importantly though in both reactions the same lone pair on the nitrogen atom of the NH₂ moiety is the nuclephilic lone pair which starts the reaction. The reason for this is probably due to sterics, in that this lone pair is less sterically hindered and can therefore more easily attack the carbonyl and the C=C double bond respectively.

Computational Analysis

The geometries of the two products 17 and 18 were optimised to find the lowest energy conformations. Initially both the MM2 and MOPAC/PM6 force fields were used to "tidy up" the structure before the final optimisation using the Gaussian (mpw1pw91/6-31g(d,p)) method. Again ChemBio3D Ultra 12 was used to calculate the energy. Using the Gaussian optimised geometry the ¹³C, ¹H NMR and IR spectrums were predicted.

Optimised Structure	Total Energy/ kcal mol-1
	24.4
	19.3

Due to the highly rigid structure of the fused rings there was very little room for any conformational flexibility. All three rings and the carbonyl were planar in both molecules and the only groups that changed during the optimisations were the methyl groups which made a negligible difference to the total energy calculated. The total energy values quoted above were from the MM2 force field optimisation the structure did not change after the Gaussian optimisation but the data was used to calculate the predicted ¹³C NMRs.

The data above suggests that molecule 18 is the more thermodynamically stable product as it was lower in energy by 5.1 kcal mol^-1. This can be somewhat rationalised from the respective yields found in the literature which stated that when the N-substituted hydrazine free bases were used the reaction yield was 100% for molecule 18. Whereas when the acidic N-substituted hydrazine hydrochlorides were used molecule 17 was only obtained in a 60% yield.

¹³C NMR

The ¹³C NMR spectra was predicted using the Gaussian mpw1pw91/6-31(d,p) or GIAO method. The literature spectra showed differences between the two regioisomers of the reaction therefore the predicted NMR spectrums should also show the same differences. This will be used to decide whether or not ¹³C NMR can be effectively predicted by a computer. The carbon atom assignments are as follows.

C atom assignments for molecules 17 and 18

Product 17				Product 18
Carbon Assignment	Predicted δ / ppm	Literature δ / ppm	Difference in δ / ppm	Carbon Assignment	Predicted δ / ppm	Literature δ / ppm	difference in δ / ppm
C-15	16.1	12.8	-3.3	C-15	11.6	10.5	-1.1
C-16	28.3	28.9	0.6	C-16	28.1	28.4	0.3
C-17	40.4	39.9	-0.5	C-17	38.0	36.4	-1.6
C-5	110.9	112.5	1.6	C-9	110.3	109.4	-0.9
C-9	111.6	110.9	-0.7	C-3	112.4	114.9	2.5
C-3	112.7	115.8	3.1	C-5	114.3	115.7	1.4
C-1	118.0	122.0	4.0	C-1	118.0	122.0	4.0
C-6	121.3	122.8	1.5	C-6	120.3	122.5	2.2
C-2	126.5	127.9	1.4	C-2	125.1	129.0	3.9
C-4	136.4	139.8	3.4	C-4	135.1	139.0	3.9
C-10	136.4	139.7	3.3	C-12	139.2	141.1	1.9
C-12	143.9	147.4	3.5	C-10	141.8	144.7	2.9
C-8	153.2	159.3	6.1	C-8	153.8	160.0	6.2

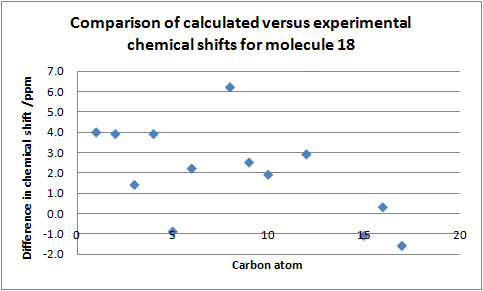
¹³C NMR data for molecule 17: DOI:10042/to-7416 , and 13C NMR data for molecule 18:DOI:10042/to-7417

From the graph it is clear to see that the calculated ¹³C NMR chemical shifts are in good agreement with the literature values with one or two exceptions. In some cases there is quite a significant difference between the calculated value and the literature value but between regioisomers show a very similar trend. For example the carbon atom labelled C-1 from the literature was expected to have an identical chemical shift (122.0ppm) since it is quite far from the regioselective centres (N-14 and 13). This was in fact observed in the calculated spectrum as the chemical shift was identical (118.0ppm) albeit the difference between literature and calculated value was quite large (4.0ppm). Again this is also seen in molecule 17 for the carbon atoms labelled C-4 and 10 whereby their chemical shifts were expected to be very similar (139.8.4 and 139.7ppm) from the literature. This clearly demonstrates the effectiveness of the ¹³C NMRs predictive capabilities as the calculated chemical shifts were 136.4ppm. Since the calculated chemical shifts match fairly well to the experimental values it would also be a reasonable assumption to say the structure of the molecule calculated by Gaussian is quite similar to that of the actual structure quoted in the literature.

In order to use the ¹³C NMR to distinguish and determine which regioisomer was produced in a reaction you would need to examine which chemical shifts change the most from one regioisomer to the other, therefore both the difference between the literature values and the calculated values were plotted.

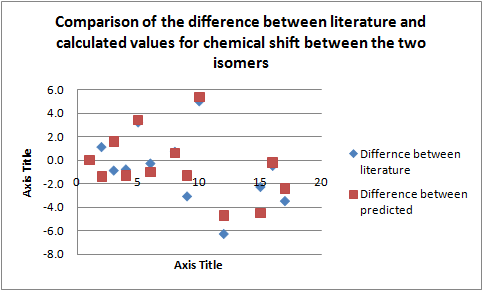
From the above graph it is seen that the largest differences in chemical shift quoted in the literature are very similar to those calculated therefore carbon atom labelled C-15, C-5, C-10 and C-12 (i.e. the carbon atoms closest to where the methyl group is situated on N-14 and N-13 respectively)can be used to distinguish between isomers. The reason these carbon atoms see the largest change in chemical shift between regioisomers is because of their proximity to the methyl group which changes the electron density near the nucleus and thus the chemical shift. It should be noted however the largest difference between chemical shifts expected was 6.3ppm (C-12) the largest difference calculated was 5.0ppm and although these values are relatively small the fact a significant difference was calculated simply from the knowledge of the structure clearly shows that ¹³C NMR can be used to distinguish between regioisomers.

One of the main problems with the calculated chemical shifts and the main reason why there is often a large difference between calculated and literature values is due to conformational flexibility. Since all the calculated values are based on a single structure where the atoms do not move whereas experimental NMR takes into account all the conformations to give an average signal.

¹H NMR and ³J_H-H coupling constants

Product 17					Product 18
Hydrogen Assignment	Predicted δ / ppm	Literature δ / ppm	Predicted 3JH-H coupling constant/ Hz	Literature 3JH-H coupling constant/ Hz	Hydrogen Assignment	Predicted δ / ppm	Literature δ / ppm	Predicted 3JH-H coupling constant/ Hz	Literature 3JH-H coupling constant/ Hz
C-15	2.38-2.75	2.66 (s, 3H)	-	-	C-15	2.35	2.75 (s, 3H)	-	-
C-16	2.88	3.69 (s, 3H)	-	-	C-16	2.86	3.66 (s, 3H)	-	-
C-17	4.24	4.30 (s, 3H)	-	-	C-17	3.95	4.00 (s, 3H)	-	-
C-1	7.70	7.30 (ddd, 1H)	8.2, 8.2	8.0, 7.8	C-1	7.62	7.25 (ddd, 1H)	8.2, 8.2	7.8, 7.2
C-3	7.75	7.43 (dd, 1H)	8.2	8.4	C-3	7.65	7.33 (dd, 1H)	8.2	8.6
C-2	8.00	7.56 (ddd, 1H)	8.2, 8.2	8.6, 7.8	C-2	7.87	7.49 (ddd, 1H)	8.2, 8.2	8.6, 7.2
C-6	8.50	8.04 (dd, 1H)	8.2	8.0	C-6	8.63	8.20 (dd, 1H)	8.2	7.8

The table demonstrates that calculated ¹H NMR spectrums was not very useful in distinguishing between the regioisomers. Firstly the calculated spectrums themselves did not match the literature very well and it was often found that peaks were observed corresponding to single hydrogens on methyl groups instead of a single peak. Furthermore the ¹H NMR spectrums of the regioisomers do not differ significantly to be able to determine which isomer is which. one of the main drawbacks of using these calculated ¹H NMR spectrums is that the multiplicities of the peaks cannot be resolved, however the vicinal coupling constants (³J_H-H) can be calculated using Janocchio). Unfortunately though in both products the six memebered ring must be too rigid as identical coupling constants were seen for every ³J_H-H coupling whereas this was not the case from the literature. This therefore implies that the structures obtained from the Gaussian geometry optimisation do not represent accurately enough the actual structures of the products.

Infrared Spectrum

The two infrared spectrums obtained were very similar since the same functional groups are present in both regioisomers. Also due to the large error associated with the calculation of the stretching frequencies in particular (8%) this makes the calculated infrared data highly inaccurate. As a result of this infrared vibrational frequencies should not be used to distinguish between the regioisomers. Furthermore the vibrational frequencies quoted in the literature were very similar for the two regioisomers.

Calculated Vibrational Frequencies

Vibration	17 / cm-1DOI:10042/to-7432	18 / cm-1DOI:10042/to-7433	Lit./ cm-1 17	Lit./ cm-118
C-H Stretch	3046	3045	2936	2927
C=O Stretch	1759	1745	1651	1656
C=C Stretch	1624	1638	1577	1592
C-N Stretch	1496	1492	1497	1426
CH3 Deformation	1462	1468	1328	1342

The data shows the stretching frequencies calculated were all higher than their corresponding literature values as described earlier from the 8% error associated with their calculation. However the data is in agreement that that the two regioisomers have similar vibrational frequencies as predicted in the literature.

Nuclear Overhauser Effect

The Nuclear Overhauser effect is transfer of spin polarisation from one population to another via cross relaxation in NMR spectroscopy it differs from coupling of spins (calculated earlier) in that the NOE effect is observed through space rather than through bonds. This allows a better description of the 3D structure than normal spin coupling as atoms only have to be close to one another to see a strong NOE effect rather than bonded. NOE is used in NOESY spectroscopy a 2D spectroscopy technique and was used in the literature to distinguish between which regioisomer was formed in the reaction. The distance information derived from NOSEY spectroscopy comes from the fact that the intensity of the NOSEY cross peak relating two protons is inversely proportional to the sixth power of the distance between them. Therefore the stronger the cross peaks the closer the proximity of the protons. In the literature it was reported although no values were stated that for molecule 17 there was a strong NOE effect observed between the proton attached to C-6 and the protons of the methyl group of C-17 attached to N-14 of the pyrazole ring. This would make sense from the structure of 17 and from the optimised structure which shows the protons in very close proximity. The relative NOE effect can be calculated using the same program that was used to calculate the coupling constants, although the values are relative to a reference from a known bond distance. Since there are no values to compare them to the distance and calculated NOE values are as follows. There was a strong NOE effect (<2.7 Angstroms) observed between the proton at C-6 and the protons at C-17 of 0.68 giving a bond distance of 2.27 Angstroms. This was the conclusion found in the literature hence this was assigned molecule 17. Similarly there was a strong NOE effect observed between the protons on C-15 and the protons on C-17, NOE was found to be 0.12 with bond distance still in the strong region (2.72 Angstroms). Again the same NOE effect was observed in the literature and so this structure was assigned molecule 18. The reference used in both cases was the H-H bond distance on the benzene ring since it was identical in both regioisomers (2.49 Angstroms).

Conclusion

This report has demonstrated how computers can be used to predict many useful properties of many different organic molecules. The mini project has shown how many different spectroscopic properties can be estimated with reasonably accuracy and how this data can be used to distinguish between regioisomers.

Although many of the techinques have fundamental flaws with continued research improvements could be made and improvements to basis sets, density functions etc will show that computational chemistry can be a very powerful, accurate and quick method for predicting the outcome of many organic reactions.