Rep:Mod1:llama2822

Computational Labs Module 1: Organic Chemistry

Introduction

This wiki page reports a number of computational experiments done between the 22nd February and the 5th March. They comprise of four introductory experiments involving simple conformational and stereochemical analysis which is then followed by a mini-project showing various spectral calculations obtained from various computational techniques. Each experiment has a separate discussion; regarding inferences from the results obtained and additionally reports and possible reasons for them, a results section which mainly consists of data tables and graphs and finally an experimental section which gives a method and specifications of the code and programs used.

The Hydrogenation of Cyclopentadiene Dimer

This first segment looks into the dimerization reaction of cyclopentadiene and determines which product is dominant via analysis of their conformational energies. From this the thermodynamic and kinetic products can be identified. The endo product can be hydrogenated into the fully reduced tetrahydrodicyclopentadiene system. However it is found that one of the double bonds is reduced more readily than the other, therefore it will also be investigated via computational techniques.

Discussion

Figure 1; Clockwise from top left; Endo, Exo, Form 3, Form 4

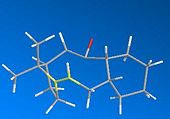
Formation of endo-dicyclopentadiene

The dimerization of cyclopentadiene readily occurs at room temperature through a diels alder reaction. By analysis of the mechanism two distinct forms can be synthesised and initial experiments showed that the endo form is favoured. Usually diels alders reactions are not reversible and only product this endo product, however this dimerization reaction can produce the exo form via heating of the system.

Figure 2; Interaction lowering the endo transition state

The calculations performed in ChemBio3D show that the endo product is 2.12kcalmol^-1 higher than the exo form (Table 1). This shows that the exo form is the thermodynamic product which is preferred when the reaction is heated. However it is shown that the endo product is produced at lower reaction temperatures, meaning that this is a result of a kinetic pathway with a lower energy transition state. Stabilization of this transition state is a result of a favourable interaction between the HOMO (Ψ3) of one of the Cp rings and the non-participating alkene and its LUMO (Ψ4) segment, which stabilises the endo transition state relative to the exo (figure 2).

Hydrogenation of endo-dicyclopentadiene

With the endo form preferred in the diels alder reaction the alkene bonds can be reduced to its alkyl form. From the results table Form 4 is 4.53kcalmol^-1 lower in energy than Form 3, showing that the stability of the molecule is increased more with the removal of the cyclohexene alkene (Form 4) compared to Form 3. This removal is favoured due to the bridgehead strain which minimises the double bond geometry away from 120^o. This is supported by the work done by Bartlett. The removal of the Cp alkene is harder to remove due to it being sterically hindered by the bridgehead carbon, therefore this reaction proceeds again via a kinetic pathway to give Form 4 and then the fully hydrogenated tetrahydrodicyclopentadiene. Enthalpic terms support the cyclohexene alkene being more labile with an enthalpy of -138.8kJ/mol^-1 compared to 109.5kJmol^-1.

Results

	Diels Alders Product		Hydrogenated Product
	Exo Product	Endo Product	Form 3	Form 4
Stretch /kcalmol-1	1.28	1.25	1.27	1.10
Bend /kcalmol-1	20.59	20.84	19.78	14.53
Torsion /kcalmol-1	7.64	9.52	10.88	12.51
van der Waals /kcalmol-1	4.24	4.34	5.64	4.50
Total Energy /kcalmol-1	31.88	34.00	35.69	31.16

Table 1; Showing the calculated energies of the dimerization and hydrogenated product

Experimental

ChemBio3D Ultra (ver. 12.0) software was used with the Molecular Mechanics (MM2) force field code used to calculate the dimer energy in kilocalories per mole (kcalmol^-1). Note that these numbers are not the molecule’s enthalpic value and are only relative to the other calculations performed in this force field; therefore comparison of the different dimer energies can be acceptable, but not with literature values.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD⁺ analogue)

Moving on from using the MM2 force field for calculations to minimise the energies of molecules this second section will introduce the MMFF94 force field. By using this on the NAD⁺ analogue the highly stereoselective addition in the para position for which NAD is famed can be discussed. The geometry of the analogues and their relative energies will also be discussed.

Discussion

NAD⁺ is a vital molecule in organisms which have a role in hydrogen transfer for redox reactions. The hydrogen adds to the para position on the pyridine ring and as a result loses the aromaticity of the ring resulting in the NADH product. In recent years many models such as those being discussed have been used to try and understand the very high stereospecifity of the hydrogen transfer in the redox process. In this segment two analogues have been modelled using MMFF94 and possible explanations of the observed stereochemistry have been reported.

Figure 3; Reactant 5 and mechanism of formation with chelation of the metal ion

Geometry of Reagents

Ring Conformations

As shown in the results table (Table 2) only one extra conformation could be determined from the two reactants which is that of the conformation of the flipped 5 membered ring in reactant 5 (Figure 3). This results in a 0.53kcalmol^-1 increase in energy. This is due to the large 7 membered ring connected being relatively flexible, therefore allowing ring flipping with only a small cost in energy. If the 7 membered ring was reduced to a six or five membered ring this ring flipping energy would increase as these rings will less flexible. A possibility of why the ring flipped version is higher in energy is that a hydrogen on the carbon alpha to the nitrogen is closer to the carbonyl oxygen (2.56Ǻ) which also results in a longer amide linkage (1.377Ǻ) compared to the alternative, non ring flipped lower energy version of (2.732Ǻ) and (1.373Ǻ).

Carbonyl Orientation

The carbonyl group of reactant five and its ring flipped conformation both point above the plane of the aromatic ring and other than the flipped ring, the conformations are identical which is supported by the similarity in energy. The carbonyl group is stabilised by the lone pair on the Nitrogen into the pi* orbital of the carbonyl. The carbonyl of reactant 7 (Figure 4) also points above the rings however it is of a lower angle. This could potentially be due to the lack of the oxygen in the 7 membered ring, which reduces the twisting of the ring. Also the addition aromatic ring is in the same orientation as the pyridinium ring however it slightly below it and slightly bent to conform with the larger ring.

Stereochemistry Determination of the Products

Reactant seven forms the most stable enantiomer R when reacted with Phenylamine. This is due to the electronegative atoms of the carbonyl and amine are pointing away from each other giving an energy of 42.80kcalmol^-1 compared to the S enantiomer of 50.22kcalmol^-1. This lowers the dipole of the final molecule with the nitrogen and oxygen pointing away from each other. Additionally sterics between these two groups in the S form also contribute to R being the more stable of the two. In comparison Reactant five forms the R enantiomer when reacted with magnesium methyl iodide despite the S enantiomer being slightly more stable (0.83kcalmol^-1). By looking at the mechanism this is due to the magnesium coordinating to the carbonyl oxygen and pointing up, whilst the methyl anion attacks the pyridine ring in a classic 6 membered Grignard reagent transition state.

Figure 4; Reactant 7 and mechanism of formation

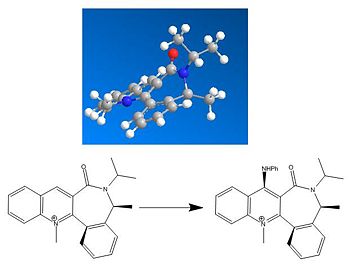
Results

	Reactants			Products
	Reactant 5	Reactant 5 Alt.	Reactant 7	Product 6	Product 8
Total Energy/kcalmol-1	59.16	58.63	85.24	/	/
R Enantiomer Total Energy /kcalmol-1	/	/	/	39.98	42.80
S Enantiomer Total Energy /kcalmol-1	/	/	/	39.15	50.22

Table 2; MMFF94 results from the NAD⁺ Analogue

Experimental

For this section ChemBio3D Ultra was used and the MMFF94 force field was run to minimize the energy of the reactant 5 and reactant 7. Further to this the Cp ring was flipped to provide an alternative, higher energy. No alternative configurations could be found for reactant 7. The two products were modelled and both enantiomers were minimized to compare these values and determine partly the enantiomer preference of the reactions shown. With respect to the first reactant when the reagent was added to the modelling system the minimization could not run. This is due to the Magnesium atom not being recognised by the MMFF94 force field and therefore cannot be considered. A possible program that could be used instead of the MMFF94 method is the gaussian optimization method by first using an MM2 force field to optimize the geometry in ChemBio3D Ultra and then creat an input file to run in gaussian as an optimization. This is a more thorough method which will be used later in this module.

Intermediates in the Synthesis of Taxol

Taxol is a chemotherapy drug commonly used in the treatment of ovarian and breast cancer. In this segment an intermediate in the synthesis of Taxol will be considered comprising of an 8 and 6 membered ring. Two major isomers arise in this intermediate which depend upon the orientation of the carbonyl group either pointing up or down. A smaller change in the 6 membered rings from boat to chair conformation can also be made. However the chair cannot be ring flipped due to its binding on two sites. The force field MMFF94 will be used primarily however an analysis will be done with MM2 and look at the comparisons between the two.

Discussion

Geometry of the carbonyl group

As shown in table 3 there are two distinct isomers of this intermediate, depending on the carbonyl group in the larger ring. Isomer 9 has the carbonyl group in the higher energy position pointing upwards with an energy of 77.97kcalmol^-1 compared to the lower energy 66.47 kcalmol^-1 with the carbonyl pointing down. This is due to the former conformation having a very strained bond angle of the carbonyl group which strains the larger ring.

Conformation of the cyclohexane ring

As shown in the results table the boat conformation can transform into the chair conformation and two inferences have been identified. Usually the chair conformation is the more stable one due to the reduced sterics of the system. For both isomers this statement is true, for isomer 9 this yields an energy difference of 7.44 kcalmol^-1 and isomer 10 of 5.03 kcalmol^-1. This energy gain could potentially be due to the relaxing of the bond strain at the carbonyl carbon resulting in a lower energy molecule.

Differences of the MM2 and MMFF94 force field

As shown the MM2 force field gives roughly the same differences between the molecules relative to its energy zero. However there are two differences, for the boat and chair conformations the variation in the energy difference for isomer 9 by MM2 is 2.14kcalmol^-1 lower than the MMFF94 whereas for Isomer 10 there are almost identical energy differences for the fields. Additionally for the energy difference between Isomers, the MMFF94 field calculates the difference 5.71 and 3.6kcalmol^-1 higher than it's respective MM2 calculation between the boat and chair isomers respectively.

Hydrogenation of the alkene bond

By modelling of the products of this hydrogenation (that of the R and S enantiomers at the bridgehead carbon) the energies for Isomer 10 are 102.34 and 72.76kcalmol^-1 for R and S respectively. Both of these energies are substantially higher than the 61.23kcalmol^-1 observed in the starting material. This could potentially be due to the decreasing distance between the methyl groups on the 5 membered ring and one of the ring hydrogens. The closest hydrogen nearest the methyl protons are 1.897Ǻ for the product and 2.045Ǻ for the reactant, therefore the hydrogenation actually decreases the stability of the molecule.

Hyperstable alkenes

Hyperstable alkenes occur in medium size rings where alkene is actually more stable with respect to strain energies than its respective alkyl derivative. This olefin strain energy is actually negative which arises to its hyperstability. Experiments done by McEwen supports the inference that the bridgehead alkene hydrogenates very slowly by stating that trans-cycloalkene in 9- or 12-membered rings exhibit hyperstability.

Results

Isomer	9	10
Boat Conformations
MM2 Total Energy /kcalmol-1	54.19	48.22
MMFF94 Total Energy /kcalmol-1	77.97	66.31
Chair Conformations
MM2 Total Energy /kcalmol-1	48.89	43.19
MMFF94 Total Energy /kcalmol-1	70.53	61.23

Table 3; Alternative Intermediates in the Synthesis of Taxol, note alkene FG coloured in yellow

Experimental

Structures of the two isomers were drawn up in ChemBio3D and their geometries minimized by both MM2 and MMFF94 force fields. The conformations adopted first were that of the boat conformation of the six membered ring and these were changed to form chair conformations and their geometries minimized by the same two force fields.

Regioselective Addition of Dichlorocarbene

This section of the report will model a bicyclohexene derivative with a chloromethylene bridge and calculate the energy surfaces of molecular orbitals to shed light on the reactivity of the molecule towards both nucleophiles and electrophiles. A geometry optimization will be run to produce the most stable form and then the molecular orbitals will be calculated via a MOPAC/PM6 method and then the surfaces analysed. Furthermore this molecule with the corresponding mono-alkene will then be formatted into a gaussian input file and the frequency vibrations optimized producing a calculated IR spectrum. These two molecules will then be compared and the varying vibrations of bonds within the molecule due to changing electronic effects will be deduced.

9-Chloro-1,4,5,8-Tetrahydro-4A, 8A-Methanonaphthalene

Molecular Orbital Calculations

Discussion

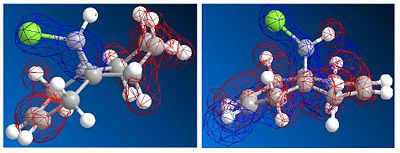
The molecule shown is labile to both electrophilic and nucleophilic additions. These two additions depend on the HOMO and LUMO respectively. By looking at the resulting molecular orbitals from the MOPAC calculation it is clear that for the homo, the majority of the highest occupied molecular orbital are based on the alkene below the chlorine. These large lobes on the alkene make it very susceptible to attack by the electrophile due to its high electron density. In contrast by looking at the LUMO of the molecule, it is dominated by the alternate alkene, making this alkene susceptible to nucleophilic attack into this unoccupied orbital.

The difference in energy of these orbitals is dominated by the presence of the chlorine group over one of the alkenes. This strongly electronegative atom has its valence orbitals deep in energy and stabilises the nearer of the two alkenes. Therefore this orbital with the chlorine orbital contribution lies deeper in energy, and is designated the HOMO. In comparison the LUMO is placed away from the carbon chlorine bond and therefore there is no stabilization effect felt.

The same can be said for the orbital designated LUMO +1. This orbital is destabilised by the chlorine atom and is higher in energy than that of the LUMO, which is dominated by the alkene away from the chlorine atom.

Hydrogenation of the allylic bond

All hydrogenation reagents are effectively "H^-" in nature, meaning that they react via nucleophilic addition. This nucleophilic addition will occur via the LUMO of a molecule, by inserting it's electrons into an unoccupied orbital and destabilising the double bond. Therefore the lowest unoccupied orbital that this "H^-" species can interact with is the LUMO, which resides over the alkene anti to the chlorine, therefore it is this bond that reacts first. If the other allylic bond were to be hydrogenated first, the nucleophile would have to place its electrons into the LUMO of that alkene. The first unoccupied orbital which has any reasonable density across this endo alkene is that designated LUMO+1 which as discussed, is higher in energy. Therefore the incoming nucleophile would prefer the lower energy LUMO, resulting the the hydrogenation of the anti bond.

Dichlorocarbene addition

Comparatively all carbene molecules are electrophilic and will interact with the HOMO meaning that their alkene of preference is that of the endo alkene which is dominated by the HOMO. The dichlorocarbene, being a singlet would first interact with the HOMO via it's empty p orbital between the double bonds, and then attack the LUMO +1 as opposed to the LUMO, due to the lack of density on the reacting carbon. The resultant species would then be a cyclopropane. The involved mechanism would be one concerted step rather than the radical addition displayed by triplet carbenes.

Results

Molecular Orbital
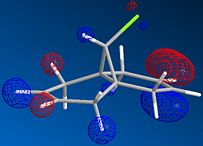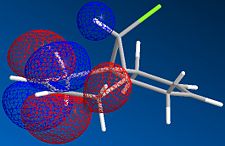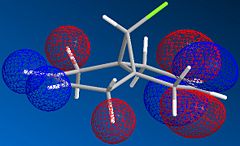Designation	HOMO -1	HOMO	LUMO	LUMO +1	LUMO +2

Table 4; Showing the calculated Molecular Orbitals of 9-Chloro-1,4,5,8-Tetrahydro-4A, 8A-Methanonaphthalene

IR Spectrum Determination

Discussion

C-Cl bond stretch analysis

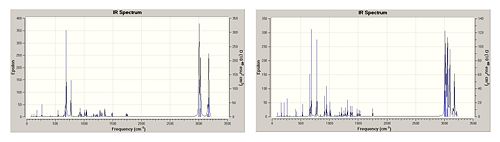
From the IR spectra (Figure 6) it shows that the dialkene has a C-Cl vibration energy of 770.9cm^-1 which is 8.1cm^-1 lower than the hydrogenated monoalkene. From this inference it can be said that the hydrogenation of the exo double bond has strengthened the C-Cl bond as it's vibrational frequency is larger. However the calculated bond length is slightly longer, which goes against this inference. The removal of the double bond could potentially strengthen the C-Cl bond by destabilising the LUMO+1 orbital, increasing its energy, as this has the antibonding component of the sigma bond of the C-Cl. This can be supported by figure 5. By looking through the calculated molecular orbitals, the HOMO-5 of the dialkene shows the high sigma bonding interaction of the C-Cl bond compared to the HOMO-29 of the monoalkene. This deepening in energy of the C-Cl sigma bond in the monoalkene compared to the dialkene strongly supports a strengthening of the bond, however this is only relative to the molecule's respective HOMO and LUMO orbitals.

Figure 5; (Left to Right) HOMO-5 of the dialkene), HOMO-29 of the monoalkene

C=C bond stretch analysis

The stronger of the two allylic bonds in the dialkene is that of the endo alkene, which is confirmed both by the higher energy of vibration (1757.4cm^-1 compared to 1737.1cm^-1) and it's corresponding bond length (1.3355Ǻ compared to 1.3319Ǻ). This supports the reported stabilisation of the allylic bond described earlier when the molecular orbitals were compared. Compare this endo bond with that of the hydrogenated product, it loses some of it's stabilisation energy, which is supported by the lower wavenumber vibration and it's slightly longer bond length. By measurement of the distance between this double bond and the chlorine atom, in the monoalkene derivative the distance is slightly less (3.254Ǻ compared to 3.543Ǻ) which could potentially rise to destabilisation of the double bond by the close proximity of the chlorine atom.

Results

Figure 6; IR Spectrum of (From Left to Right) Dialkene, Monoalkene

Dialkene				Monoalkene
Bond Length/Ǻ	Wavenumber/cm-1	Mode #	Vibration	Mode #	Wavenumber/cm-1	Bond Length/Ǻ
1.7889	770.9	19	C-Cl stretch	20	779	1.7904
1.3355	1737.1	55	exo-allylic stretch	/	/	/
1.3319	1757.4	56	endo-allylic stretch	60	1753.8	1.3327

Table 5; Showing the vibrational stretches of the di- and mono-alkene

Experimental

Molecular Orbital Calculation

In ChemBio3D Ultra the 9-Chloro-1,4,5,8-Tetrahydro-4A, 8A-Methanonaphthalene was drawn and the geometry optimised with MM2 code. Further to this the Mopac interface was used to map out the molecular orbital surfaces using MOPAC/PM6, and the HOMO, HOMO-1, LUMO, LUMO+1 and LUMO+2 were displayed using a wire mesh surface and at higher resolution.

Calculated Hypothesised IR Spectrum

From consideration of the orbitals the monoalkene was also created and had the same treatment. These two molecules which are PM6 optimised were then subject to the Gaussian interface, running a DFT method with B3LYP hybrid functional and 6-31G basis set. Polarisation was set to d and H: to the p form and the input file was formatted so the top line read ‘# b3lyp/6-31G(d,p) opt freq.’ This was run on SCAN under queue Chem Lab 1 and took ca. 30 minutes. The Formatted Checkpoint file was downloaded and opened in Gaussview 5.0 where the calculated IR spectrum and subsequent stretches could be determined. Vibrational modes are correlated from the gaussian interface and the bond lengths have been determined from the gaussian optimization.

Final Project; Calculation of spectra for Trans-Substituted Cyclopentenes via Cope Ring-Opening Rearrangement

Introduction

This final segment of this page documents the computational experiment of calculating the spectra of a literature compound, and comparing the experimental values with that of the calculation. A recent article was picked from the Journal of Organic Chemistry which contained a reaction producing a product which was not highly flexible and had associated ¹³C NMR values. Additionally the product have to have scope to be a stereospecific reaction with the potential for isomerization. The product in its major isomer will be modelled and changed to identify possible other stable conformations. Following on from this the other isomeric products will be modelled and two will be forwarded for geometric optimization by the program Gaussian. From this the NMR spectra will be calculated, including the ¹³C and also the ³J coupling constant values. Furthermore the IR will be calculated and from the experimental data in the literature, the preferred conformation will be identified.

Article Discussed

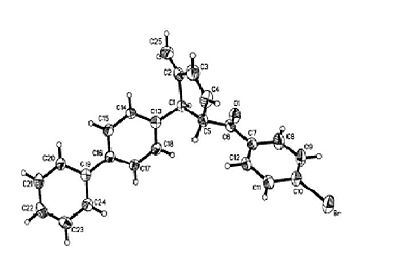
The proposed article for analysis is from the Journal of Organic Chemistry and submitted by Xiang-Ying Tang from the Chinese Academy of Sciences. The article documents the synthesis of methylenecyclopropanes via a Wittig reaction, followed by a thermally induced rearrangement to form a stereospecific cyclopropene ring with a variety of substituents. The molecule chosen contains a para substituted bromobenzaldehyde group and a biphenyl group, which through consideration of the mechanism adopt a trans arrangement on adjacent carbons on the cyclopentene ring. The compound, labelled 2p by the author additionally has X-ray crystallography information available in the supporting information.

Discussion

Mechanism

The precursor to the Cope rearrangement can be synthesised via Wittig reaction of a propanecarbaldehyde and the appropriate ylide. The negative charge on the ylide can resonate with the adjacent benzaldehyde and due to this stabilization the allyl product produced is of E regiochemistry. The waste product produced is the high molecular weight phosphate oxide which precipitates out of the toluene solvent. Following this the Cope rearrangement is thermally induced under an Argon atmosphere to yield the cyclopropane ring opened cyclopentene product.

This reaction was initially thought to be a radical initiated reaction, however adding TEMPO to the reaction mixture did not affect the products formed so it is not speculated that it occurs via a cope rearrangement. This pericyclic reaction is supported by it being thermally induced and additionally having small solvent effects on yield and stereoselectivity, with yields only varying by around 5% for a wide range of solvents.

Formalisation of the reaction

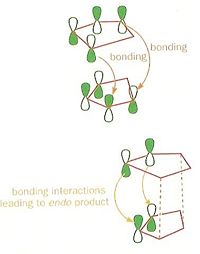
As discussed the reaction is a cope rearrangement (figure 7) which is thermally induced. This is a [3, 3] sigmatropic rearrangement which shows conrotation of the substituents on both of the sp² carbons giving an s shaped bond forming which leads to antarafacial component in the reaction. Due to the six electrons involved in the rearrangement and the thermally induced reaction it leads to the Hückel Transition State. However this Hückel state requires either a suprafacial component or two antarafacial ones, meaning that the breaking of the cyclopropane ring occurs in an antarafacial way.

Figure 7; Mechanism of the Ring-Opening Rearrangement and preceding Wittig reaction and Transition State of the Ring-Opening Rearrangement

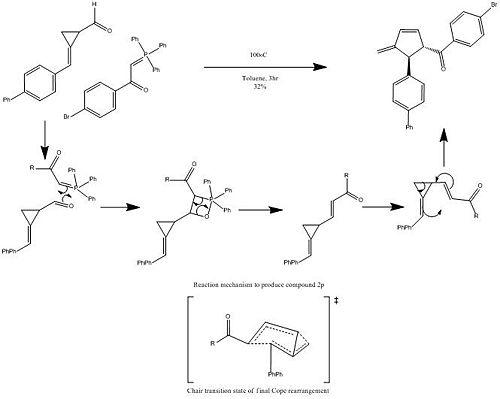
The control of the stereochemistry is dependent of the regiochemistry of the formed alkene bond in the Wittig reaction, whereby if the alkene is of E regiochemistry the formed product will be that of the trans cyclopentene product. If a Z alkene is used the product produced will be the cis product; however the journal states that due to the high steric interactions between the two groups the product will automatically rearrange into the trans cyclopentene product.

The precursor to the thermally induced rearrangement can actually be made in situ by heating the initial products under Argon. The phosphate oxide waste product precipitates out of the reaction and results in the rearrangement happening instantaneously.

Isomeric Products

As detailed in the mechanism section, the only isomer that is formed is the trans product, and if the cis product was formed due to the thermal lability of the complex, it will rearrange into the trans isomer. All four isomers have been modelled and from looking at the pericyclic mechanism, only one isomer can be determined. However if a Z alkene is used the sterochemistry of the carbonyl group can be changed, with the two substituents being cis on the ring. However it states in the article that the product must automatically rearrange to form the trans isomer which has been confirmed spectroscopically. However two isomers will be considered, that of the trans isomer and also that of the cis. Additionally an alternate conformation of the trans isomer will be modelled and all the spectra compared with the literature.

Isomer	I	II	III	IV
Stereochemistry at C1	R	S	S	R
Stereochemistry at C5	S	S	R	R
MMFF94 Total Energy /kcalmol-1	113.53	118.17	115.76	118.48
Jmol popout Images

Table 6; Table showing the isomer energy of compound 2p

Product Conformation

The molecule was chosen in light of its relatively rigid structure, with a large amount of aromatic rings and a cyclopentene ring which cannot be flipped. However there are a variety of conformations which will be modelled and analysed before choosing two to move onto the spectral calculations.

Biphenyl Ring Conformation

The first inference is the biphenyl rings which, due to it being unsubstituted, has a torsion angle of 40.4^o. For the simple biphenyl molecule the energy barrier for torsion being 1.65 kJ mol^-1 and an experimental torsion angle of 42^o. This 4^o error is relatively small and is not due to any interactions as the second ring being so far out in space. A calculated value using a Molecular Mechanics method returned a result of 42^o. From the article's supporting information, X-ray crystallography data shows that the biphenyl rings are 37.9^o rotated with respect to each other, which is now lower than the calculated value.

An interesting inference is the preferred slanting that is chosen by the bi phenyl group. Nearly all conformations prefer the second ring to be slating left (up) and right (down) with respect to looking down the axis of the two aromatic cycles. This is approximately in line with the C₁-C₂ bond on the cyclopentene ring. However conformation D prefers to slant right (up) left (down), pointing to the side containing the carbonyl molecule. This could potentially be due to the free space which was either occupied by the carbonyl or bromo-substituted phenyl group in all other conformations. However the preference for this slant cannot be explained.

Figure 8; Molecular structure of molecule 2p from X-ray crystallography

Cyclopentene Ring

Due to the three sp² hybridised carbons around the ring, it is completely planar with only the two substituents on the sp³ carbons providing any change. Only the trans- isomer will be considered and this is reasonable in light of the mechanism. However there is a slight twist of the ring in conformation E, due to the large phenyl ring sitting on top of the cyclopentene ring, twisting the C₅-C₁ bond to minimise the steric bulk near the ring.

Carbonyl Positioning

Again through the five conformations chosen there are a number of different conformations regarding the carbonyl geometry. Conformations A, C and E have their carbonyl positions within the plane of the bromo- substituted ring. For conformation B it can be seen that the hydrogen in the ortho- position interacts with the hydrogen at the C₅ position. The same can be said for conformation E except where the same hydrogen will interacts with the hydrogen at the C₁ position.

The orientation of the carbonyl bond also changes through the conformations with A, B and C having the oxygen pointing up, away from the biphenyl rings, D with the oxygen pointing away from the cyclopentene ring and perpendicular to the biphenyl rings and finally E where the oxygen points down, back towards the biphenyl ring.

Diagram	A	B	C	D	E
Boat Conformations
MM2 Total Energy /kcalmol-1	22.73	23.43	25.36	24.07	23.95
MMFF94 Total Energy /kcalmol-1	113.57	115.00	113.66	118.70	119.53
Jmol popout Images

Table 7; Major conformations of product 2p (Isomer I)

Spectral Analysis

¹³C NMR Analysis

The calculated spectra for all compounds can be found here (Conformation A, Conformation E, Isomer II)

General Analysis

Figure 9; Graph showing the variation of the calculated shifts of conformations with respect to the experimental data

Figures 9 and 10 show the variation of the calculated shift with the experimental values. With first comparison of the two conformations of Isomer I it shows that the variation is minimised with conformation A, the lower energy of the two. The biggest variations are of the C15-C20 carbons, based on the biphenyl rings where the correlation breaks down with a larger error in the calculation. This is common for all the calculated isomers and conformations. Additionally the paper does not document 25 shifts due to the large size and small shift change of the phenyl rings, and for that reason 5 variations are absent. One anomaly is the C10 carbon with the bromine atom attached to it does not seem to require any adjustment (usually due to uncalculated spin orbit coupling with heavy atoms such as Br).

Conformation comparison

As shown clearly in Figure 10 the conformation with the smallest difference to the experimental data is conformation A with an average variation of 2.8ppm (compared with 3.33) over all carbon environments. Conformation E fits well with A in places, however C5 (on the ring of the cyclopentene) shows a very large difference with the experimental value.

Isomer comparison

Figure 10; Graph showing the variation of the calculated shifts of isomers with respect to the experimental data

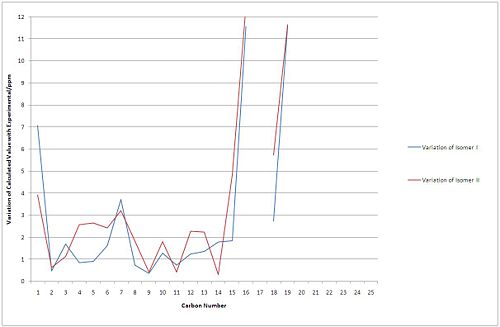
Isomer I (the formed product) shows good correlation with the experimental data as discussed above. Isomer II (the cis product) is on average 3.20ppm out per carbon atom and shows similar flaws as the other two spectra.

A full results table of the calculated ¹³C NMR can be found here.

Infra Red Analysis

		Isomer I				Isomer II
		Conformation A		Conformation E		Conformation A
Stretch	Carbons involved	Mode #	Energy/cm-1	Mode #	Energy/cm-1	Mode #	Energy/cm-1
Symmetric C-H stretch	C1, C5	115	3048	115	3055	115	3069
Asymmetric C-H stretch	C1, C5	114	3040	114	3047	114	3004
C=O stretch	C6	113	1757	113	1757	113	1760
C=C stretch	C2, C25	112	1717	112	1714	112	1717
C=C stretch	C3, C4	110	1664	109	1647	110	1661
Ar bending	C14&C15, C17&C18	43	751	43	747	43	747
C-Br	C10	41	716	42	736	41	718
Ar bending	C20&C21, C23&C24	40	714	41	714	40	714
Ar bending	C8, C9, C10, C11	39	706	40	714	39	704

Table 8; Showing the variation of particular vibrational stretches within Conformations A, E and Isomer II

Conformation A Conformation E Isomer II

Of particular note is the symmetric and asymmetric stretches of the 2 protons on the stereogenic carbons at ca. 3048 and 3040cm^-1. These show the variance of the stereocentres where the energy of vibration dramatically changes for the cis isomer where the energies are much further apart. The characteristic stretch is that of the C=O bond at 1757 however the nearest vibration reported by the article is 1685cm^-1, a considerable difference between the values gained in these calculations. This value of 1685cm^-1 is more in line with the allylic bonds in the cyclopentene. Of additional note these vibrations of the allylic bonds in and around the cyclopentene ring also vary little with the calculations except for conformation E where the stretch is remarkably low compared to the other two calculations. This weakening of the bond could be due to the hydrogen on the bromo substituted ring provide clashes with the orbitals of the alkene.

³J H-H coupling

Unfortunately the article did not report the coupling constants at the hydrogens around the ring and as shown in table 9 the coupling constants around the phenyl ring hydrogens effectively don't vary due to them being effectively isolated in free space and therefore in the same environments. However the table shows the variance of the coupling constants around the cyclopentene ring which varies due to the angle between the hydrogens. The hydrogen couplings of note is between the two stereogenic hydrogens which obviously vary for either isomer, but also varies slightly with conformation with conformation E having a slightly lower dihedral angle which results in a lower coupling constant.

	Isomer I Conformation E		Isomer I Conformation A		Isomer II
3J Linkage	Dihedral Angle/o	3J Coupling constant/ Hz	Dihedral Angle/o	3J Coupling constant/ Hz	Dihedral Angle/o	3J Coupling constant/ Hz
H-C1-C5-H	143.6	7.667	144.3	7.785	6.5	9.251
H-C3-C4-H	0	8.22	1.3	8.22	0.7	8.22
H-C4-C5-H	69.8	0.736	72	0.534	69.2	0.788

Table 9; Coupling constants between select hydrogens

Conclusions

Through computational techniques it has been confirmed predominantly by ¹³C NMR that the compound 2p is in its trans isomer, and the data also strongly suggests that the conformation of A predominates largely due to sterics rather than stereoelectronic interactions. The Carbon NMR has proved the most useful tool with a large number of carbons to correlate to with little variance in chemical shift with the calculated ones. Comparatively the IR and ³J coupling constants have proved less useful, mainly due to the lack of information within the article, however comparisons have been made and further, more detailed spectroscopic experiments could prove conclusive on the techniques discussed.

Experimental

Geometry Optimization

Using ChemBio 3D Ultra 12.0 the molecule 2p was drawn out and the first conformation drawn as in the X-ray crystallography diagram from the literature. Following this the Molecular Mechanics 2 force field was used to optimise the geometry, however it was found that the MM2 did not let the biphenyl ring substituent be twisted, which is the low energy conformation compared to the two phenyl rings in plane (due to ortho hydrogen steric interactions). Therefore the MMFF94 force field code was used and this corrected the problem, favouring the lower energy non planar biphenyl rings.

This initial conformation was changed to other conformations, in particular moving the carbonyl group pointing in different directions yielding five different conformations. From this conformation A and E were picked and from the MMFF94 geometry optimized molecule, a gaussian input file was created using Method DFT, with MPW1PW91 hybrid functional and a 6-31G(d,p) basis set. The gaussian optimization was limited to 25 cycles and the molecules were put into Chemistry Lab 2 pool which yielded an optimized molecule in 2.5 hours. Both conformations were checked against their original MMFF94 optimizations.

¹³C NMR Calculation

The gaussian optimized conformations were then resubmitted with the top line of [# mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform)] and put into Chemistry Lab 1 with the calculation taking 15 minutes and then the gaussian log file was downloaded and opened in gaussview. The NMR spectrum were automatically brought up and the carbon spectra selected defining the references as TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO. The summary of the spectra was then exported, the carbon atoms reassigned to fit the X-ray crystallography numbering and then plotted against the experimental data. From this the variation between the two was calculated and finally the variations of the isomers and conformations were compared.

IR Calculation

The gaussian optimized conformations were then resubmitted with the top line of # b3lyp/6-31G(d,p) opt freq and put into Chemistry Lab 2 with the calculation taking 2 hours and then the formatted checkpoint file was downloaded and opened in gaussview. The IR spectra were compared with each other and the experimental values and the stretches identified.