Rep:Mod1:jg1208

Modelling with Molecular Mechanics

Introduction

In computational chemistry, there are a number of approaches that allow calculation of molecular geometries, reactivities, spectra and other properties. The four most popular ones are molecular mechanics, ab initio methods, semi –empirical methods and density functional theory (DFT) methods.

In this module molecular mechanics, semi-empirical and DFT methods are employed to examine a series of reactions and molecules with comparisons to literature. A brief explanation of each approach will be given as they are introduced throughout the module.

---

Molecular mechanics is based on a model of a molecule as a collection of balls (atoms) held together by springs (bonds) . If we know the normal spring lengths and angles between them, and how much energy it takes to stretch and bend the springs, we can calculate the energy of a given collection of balls and springs (i.e. a molecule). By changing the geometry until the lowest energy is found, a geometry optimisation can be performed to find the most stable conformation of a given molecule.

Compared to other methods discussed later in this module, molecular mechanics is a cheaper, simpler and therefore quicker approach, which is therefore often preferred when chemists wish to confirm a molecule’s optimum geometry. More complicated information related to reactivity such as nucleophilic and electrophilic behaviour can only be determined from electron distribution – this is given by a molecule’s wavefunction, which can only be determined by quantum mechanical methods such as ab initio, semi-empirical and DFT.

Molecular mechanics assumes that the energy of a molecule can be split into contributions from diatomic stretches (str), triatomic bond angle deformations (bnd), tetra-atomic bond torsions (tor), van der Waals repulsions (vdw) and dipole-dipole (dip-dip):

E = E(str) + E(bnd) + E(tor) + E(vdw) + E(dip-dip)

The explicit form used for each of these contributions is called the force field (note: the usage of the term “force field” in computational chemistry differs from the standard usage in physics: In physics it is a gradient of scalar potential, while in chemistry it is a system of potential energy functions.)

For example, for the bond stretching term, E(R) = D(1-exp(-F(R-R₀))²

where D=dissociation energy, F = force constant, R₀ = natural bond length.

The parameters D, F and R₀ are part of the so-called force field, and their values are determined either experimentally, or by ab initio calculations. Analagous formulas and parameters are defined for bond angle bending, torsions, dipole-dipole etc.

Commonly used force fields in molecular mechanics simulations are MM2, MM3 and MM4. In this module, the MM2 force field was used in the ChemBio 3D program to characterise a number of reactions and molecules.

The dimerization of cyclopentadiene and its endo/exo selectivity

Fig.1 – Dimerisation of cyclopentadiene showing the exo and endo products

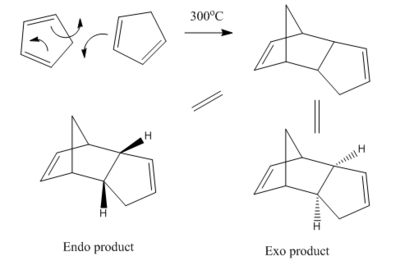
Cyclopentadiene undergoes a [4+2] cycloaddition dimerization to yield the endo product rather than the exo product as shown in fig.1. This preference for the endo was measured computationally using the MM2 force field. The total energies for each of the molecules was minimised using geometry optimisation, and the results are displayed in table 1.

Table 1: Minimised energies of endo and exo dimers of cyclopentadiene

	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 Van Der Waals	VdW	Dipole-Dipole	Total Energy
Exo	1.25	20.84	-0.84	9.51	-1.54	4.32	0.45	34
Endo	1.29	20.58	-0.84	7.65	-1.42	4.23	0.38	31.88

Fig.2 The 1,4 strain encountered by the endo product

To understand the outcome of a reaction in terms of the ratio of isomers formed, one has two consider two factors:

1. The relative stability of the products – thermodynamic factors

2. The rate of product formation – kinetic factors

Table 1 shows that the exo product is more than 2kcal/mol lower in energy than the endo product, due to less torsional strain. This is to be expected if we draw the molecules from a different perspective:

The endo product has 1,4 strain between the two carbons indicated in fig.2 – the exo product does not, so is more stable.

Fig.3 Frontier orbital explanation of endo rule

We can therefore identify the exo product as being the dominant isomer when the reaction is under thermodynamic control (higher temperatures). But under kinetic control (lower temperatures), one has to look at not at the stability of the products, but the stability of the relative transition states, i.e. how long it takes to reach them. The stabilities of transition states will be examined more thoroughly in Module 3. For now, we can give a ‘hand waving’ explanation in terms of frontier molecular orbital theory, first described by Woodward and Hoffmann. The basic idea is that the occupied orbitals of one molecule and the unoccupied orbitals of the other (particularly the HOMO and LUMO) interact with each other causing attraction (Fig 3)

Fig.4 Dimerization energy diagram

A better explanation is provided by secondary orbital interactions, which will be discussed in the mini-project later on in this module, which tackles a similar cycloaddition reaction.

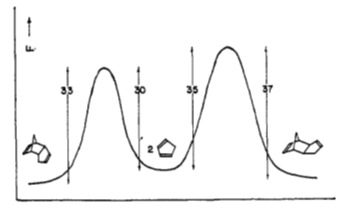
To further elucidate the distinction between the thermodynamic and kinetic products, the following graph has been taken from John Baldwin’s original paper on the dimerization. It shows the transition state of the endo product having a lower energy than that of the exo product (Fig 4)

Fig.5 Hydrogenated products (1) and (2)

The dimer can then be subjected to hydrogenation, in which the hydrogen molecule attacks one of the two C=C bonds to form either product (1) or (2): Which product will predominate? Again the MM2 force field was used to optimize the geometries of the molecules and determine which has the lowest total energy:

Table 2 - Energies of the products of hydrogenation

	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 Van Der Waals	'VdW	Dipole-Dipole	Total
Product 1	1.28	19.86	-0.83	10.81	-1.22	5.63	0.16	35.69
Product 2	1.1	14.52	-0.55	12.5	-1.07	4.51	0.14	31.15

As the table shows, product 2 is the more stable one by about 4.5 kcal/mol, with this difference largely accounted for by the difference in bending energies. How does this arise? We can answer this by examining the molecules: In product 1 the double bond is located close to the norbornene bridge, which destabilises this dicyclopentadiene, reducing the sp2 carbon bond angle from 120° to about 107°. In product 2, however, the double bond is further away from the bridge, so reduced strain means that the sp2 carbon’s bond angle is reduced by less, to around 113°. This means that product 2 is overall more stable, so we can identify this as the thermodynamic product of the hydrogenation.

---

Sterochemistry and reactivity of an intermediate in the synthesis of taxol

Taxol is an important drug in the treatment of ovarian cancer, so its synthesis and therefore structure is of particular interest to organic chemists. Paquette proposed 2 possible key intermediates (3) or (4) in its synthesis, which are differentiated by atropisomerism – that is, by restricted rotation about a single bond due to high steric demand.

Fig.6: 2 key intermediates in the synthesis of taxol

The stereochemistry of the carbonyl addition depends on which isomer is more stable – this is where molecular mechanics comes in! This time, two force fields – MM2 and MMFF94 – were used to determine the relative energies of the two isomers. The MM2 and MMFF94 approaches are both molecular mechanics methods, however, MM2 (which was invented by Allinger) uses different parameters, and is better suited to medium-sized organic molecules. MMFF94 (Merck molecular force field 94) is a more recent force field which can be used for larger biological molecules such as proteins and nucleic acids. It was found that each isomer has two distinct minimum energies, corresponding to the chair and twisted boat conformations of the analogous cyclohexane molecule. The relative energies of these conformations are shown in table 3.

Table 3: Energies of the different conformations of the two intermediates.

Conformation	Total Energy kcal mol-1		MM2 Parameter Energies kcal mol-1
	MM2	MMFF94	Stretch	Bend	Torsion	Van der Waals	Dipole-Dipole
3a Carbonyl up, chair	48,73	66.60	2.63	13.96	20.98	13.93	-1.57
3b Carbonyl up, twisted boat	53.01	77.97	2.88	17.28	20.61	14.37	-1.71
4a Carbonyl down, chair	42.69	60.56	2.51	11.33	19.67	12.88	-2.00
4b Carbonyl down, twisted boat	48.16	66.32	2.70	11.81	22.89	14.34	-2.00

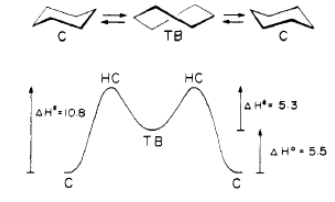
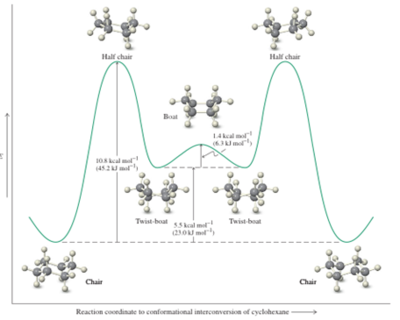
These results were obtained by manually changing the conformations of the molecules in order to minimise the repulsion between atoms due to the van der Waals force. The data shows that the largest contribution to the total energy comes from torsional strain, or Pitzer strain - this is a potential energy that is caused by cyclohexane adopting the chair structure in order to minimise the likelihood of vicinal hydrogens eclipsing each other around the ring. The MM2 and MMFF94 show similar results, although they cannot be compared directly because they use different parameters for the calculation. They show similar trends for both molecules – namely that the conformational isomers with the carbonyl up are less stable than those with the carbonyl down by 6-10kcal/mol. Within these two sets of isomers, the chair structure is more stable than the twisted boat by about 5 kcal/mol. This can be explained in terms of the hydrogen atoms bonded to the carbons - in the chair structure they are staggered so do not eclipse each other, reducing strain and therefore stabilising the molecule. Confirmation of this difference in stability is found in literature – in 1975 Squillacote et al provided an energy diagram of the ring-flipping of cyclohexane (fig.7) to show that the chair structure is the most stable conformation – the global minimum on the diagram, while the twisted boat is a less stable minimum on the energy diagram – the local minimum. A more detailed version of this diagram showing conformations is provided by Vollhardt and Schore (fig.8).

Fig.7 Squiallacote's cyclohexane energy diagram

Fig.8 A more detailed version of the cyclohexane energy diagram

Our attention now turns to the reactivity of taxol – what happens when it is functionalised? It is found that the molecule reacts very slowly, because both of the isomers (3) and (4) are bridgehead olefins which are hyperstable. According to McEwen and von Rague Schleyer, double bonds at bridgehead positions are generally destabilized by strain, but in larger polycyclic systems like isomers (3) and (4), such locations may actually be preferred – such olefins are referred to as being hyperstable, and have negative olefin strain energies – that is, the strain energy of the olefin is less than that of its parent hydrocarbon.

This unexpected stabilization by the double bond can be explained by examining the bond angle between the bridge and the ring in the most stable chair conformation. This was calculated on chembio3d for both the sp3 carbon in alkanes (which have an ideal bond angle of 109.5°) and the sp2 carbon in alkenes (which have an ideal bond angle of 120°), and is shown in table 4.

Table 4: Bridge-ring bond angles in hydrogenated taxol

Conformation	Bridge-ring bond angle (°)
	Calculated	Optimal
Product 3 (chair)	119	120
Hydrogenated product 3 (chair)	117	109.5
Product 4 (chair)	122	120
Hydrogenated product 4 (chair)	118	109.5

As shown, the sp2 carbons are within a 1-2° range of the optimal 120° bond angle, suggesting that these are quite stable. On the other hand, the sp3 carbons in the hydrogenated products have angles that differ by 8-9° from their optimal ones, so they are less stable than the alkenes.

Another reason for the increased stability of the intermediate as an alkene is the fact that at shorter distances the van der Waals interaction increases according to the Lennard Jones potential This states that at short H-H distances the interaction becomes very repulsive. This repulsive interaction is more pronounced in the alkane structures, thus increasing preference for the alkene structure.

Thus we can explain the slowness in the functionalization of this alkene by its hyperstability – it is too stable to react quickly. This in turn leads to heats of hydrogenation that are lower than normal.

As an interesting side note, it is worth noting the unusual mechanism for interconversion between isomers (3) and (4) shown in fig. 9. According to H. Rzepa the process is as follows.

Fig.9 Atropisomerism in taxol

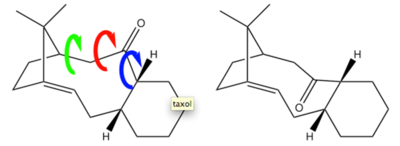
1. Firstly, the carbonyl group (red and blue bonds) rotates

2. This then stops, and the methylene group starts to rotate (green and red bonds) – at the transition state it is this motion that is occurring

3. The rotation of the methylene group then slows down, and the carbonyl group starts to rotate again (red and blue bonds)

---

Modelling using semi-empirical Molecular Orbital theory

Fig.10 Product (5)

Up until now we have used molecular mechanics to determine molecular energies – but this is a limited approach when we want accurate data which allows us to make predictions of reactivity. For this, we need to know more about the electronic distribution in a molecule, which can only be determined with a quantum mechanical approach. However, purely quantum approaches known as ab initio methods are expensive, and their solutions require calculation of complicated 3- and 4-centered integrals which were very difficult to solve quickly in the 1960s. Thus, semi-empirical methods were developed and became popular. These are also based on the Schrodinger equation, but more approximations are made in solving it, so that instead of calculating 3- and 4-centered integrals, the program draws on a library of integrals that was compiled by finding the best fit of some calculated entity like geometry or heat of formation to the experimental values. This plugging of experimental values into mathematical procedure to get the best calculated values is called parameterization, and it is this mixing of theory and experiment that makes the method ‘semi-empirical’.

Despite these large approximations, suitable parameterization can adjust answers back into a correct or at least reasonable range. One semi-empirical method that has been very successful is Huckel theory, which is a simple linear combination of atomic orbitals molecular orbitals (LCAO MO) method for the determination of molecular orbitals of pi electrons in conjugated hydrocarbon systems.

In the most simple case, the semi-empirical method used was called CNDO (complete neglect of differential overlap), and over the years this has been modified and replaced by the MNDO, MINDO/3 and AM1 methods and later by PM3 and in 2007 PM6 parameterization .

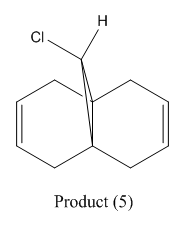
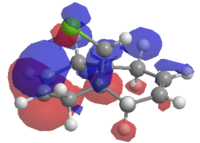
In our first application of the semi-empirical approach, the regioselective addition of product (5) (fig.10) with the electrophilic reagent dichlorocarbene (fig.11) was investigated using the PM6 method via the MOPAC program, which can make quantum calculations using a variety of semi-empirical algorithms. Following minimisation of energy by MM2, MOPAC/PM6 produced an approximation of the frontier molecular orbitals, which allows us to explain why according to Rzepa et al the dichlorocarbene adds regioselectively on to the π-face endo to the chlorine

Fig.11 Regioselective addition of dichlorocarbene

HOMO-1	HOMO	LUMO
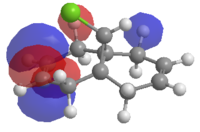LUMO+1	LUMO+2

Since the HOMO is the highest energy MO that product (5) has, it is this one which is involved in the nucleophilic attack of dichlorocarbene, and therefore the orbital that we are interested in. Examination of the MOs reveals that the HOMO is located such that it can overlap well with the endo double bond. This partly explains the regioselectivity. Further detail is provided by the LUMO+1 and HOMO-1 orbitals, which show antiperiplanar overlap of the σ* C-Cl antibonding orbital and the π-orbital of the exo double bond respectively. As noted by Rzepa et al, this stabilising interaction causes a geometrical distortion of the two rings, and causes the exo double bond orbital to be lowered in energy, so its nucleophilicity is reduced. Correspondingly, as the interaction leads to greater electron density in a C-Cl antibonding orbital, the C-Cl bond is weakened. When the dialkene is hydrogenated across the exo double bond there is no more overlap between the HOMO-1 and LUMO+1, so the interaction is lost. In principle, this should lead to shorter C-Cl bonds. The best way to confirm this is to inspect the molecule's vibrational behaviour in IR spectroscopy.

Vibrational frequencies of molecules is best studied computationally using density functional theory, which like the semi-empirical approach is based on the Schrodinger equation. However, DFT does not calculate a wavefunction, but rather derives the electron distribution (or electron density function) directly. The basic idea is that the properties of a many-electron system can be determined using functionals, i.e. functions of another function, which in this case is the spatially dependent electron density – hence the name DFT!

Although DFT methods are slower than semi-empirical ones, they are generally more accurate because electron correlation effects are built into the approximate energy functionals – this means that DFT could in theory be used to analyse the entire periodic table!

The popular B3LYP functional was used for this investigation, and the basis set was 6-31G(d,p). A basis set is a set of functions representing atomic orbitals, which are expanded in a linear combination to create molecular orbitals. Its history in computational chemistry is an interesting one: Initially these atomic orbitals were used in the Hartree-Fock method (an ab initio method) and were represented as Slater orbitals, which corresponded to a set of functions which decayed exponentially with distance from the nuclei. Later, Frank Boys realised that the Slater orbitals could themselves be approximated as a linear combination of Gaussian orbitals. These Gaussian basis functions are much easier to compute, because they reduce the 4-centre integrals found in Slater orbitals to finite sums of 2-centre integrals and then 1-centre integrals. These are around 5 orders of magnitude quicker to solve than Slater orbitals, so Gaussian basis functions are much cheaper to use.

The software used to calculate these Gaussian basis functions is called Gaussian, a software program designed in 1970 by John Pople. It is a monolithic ab initio program, which also includes some semi-empirical and molecular mechanics methods. There are a wide range of molecular properties that can be computed such as NMR chemical shifts, nonlinear optical properties, several population analysis schemes, vibrational frequencies and intensities and data for use in visualization programs.

Compound	Spectrum	Vibrations (cm-1)
Monoalkene	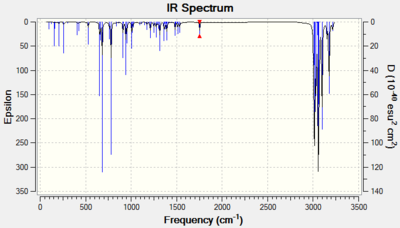DOI:10042/to-11781	C-Cl 779
		C=C 1753
Dialkene	DOI:10042/to-11787	C-Cl 770
		C=C (exo) 1737
		C=C (endo) 1757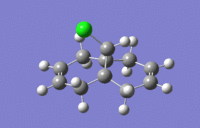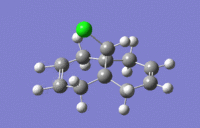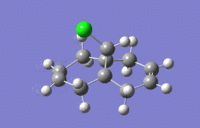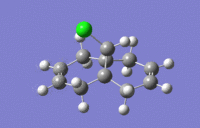
Optional with CN substituent	DOI:10042/to-11780	C-Cl 765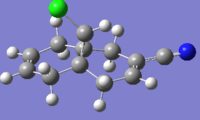
		C=C (exo) 1706
		C=C (endo) 1756

As shown in the spectra, the C-Cl vibrates at 9Hz higher when the exo double bond has been lost - this corresponds to a strengthening of the C-Cl bond, as predicted.

In addition to the above, the option to investigate substituent effects was taken. An electron withdrawing CN group was substituted onto the exo alkene, and the result was that the the C=C endo bond dropped its vibrational frequency by 1Hz, i.e. it grew weaker. This is because the CN group withdraws electron density from the double bond, which weakens it.

Glycosidation

Fischer glycosidation involves the acid-catalysed addition of alcohols to cyclic hemiacetals to form cyclic acetals at an anomeric centre. The product is called a glycoside, and the α-glycoside is favoured due to the anomeric effect: This is due to the presence of an oxygen substituent α to the anomeric carbon that makes any carbocation formed there more stable than it would otherwise be. This is an SN1 process which forms an initial oxonium ion after loss of water, followed by attack of the alcohol in the second step to give the acetal product as shown in fig.12

Fig 12 Mechanism of Fischer Glycosidation

One way to exert control over the stereochemistry of the new anomeric bond involves neighbouring group participation of an ester protecting group such as an acetate group on the 2-hydroxyl group. As shown in fig.13, following loss of the anomeric leaving group, the carbonyl oxygen of the acetate group interacts at the 2-position and can stabilise the intermediate oxonium ion by cyclisation. The nucleophile can then open the new ring by attacking from the opposite side to the large protecting group in an SN2 manner. Following deprotection of the acetate, the final result is a new anomeric linkage located trans to the 2-hydroxyl group i.e. either the α- or β-anomer depending on the orientation of the original acetate group.

Fig 13 Neighbouring group participation by acetate group

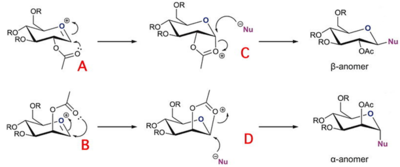
The diastereospecificity of glycosidation was modelled using molecular mechanics by the MM2 method, and using semi-empirical quantum mechanics by the MOPAC/PM6 method. Naturally, the semi-empirical approach will give more accurate results because using quantum mechanics it is able to take into account the effect of secondary orbital interactions, which MM2 lacks as it sees molecules as classical balls on a spring, not as wavefunctions.

A methyl group is chosen as the R group because it is complex enough to represent realistic chemistry, but simple enough to keep the calculations fairly quick. The simplest group of all, hydrogen, would be unsuitable here as it would engage in H-bonding.

The heats of formation of the oxonium ion rings A, B, C and D plus their ring flipped derivatives are shown in table 5.

Table 5. Heats of formation of A, B, C and D plus their ring-flipped derivatives

Contribution (kcal/mol)	A	A(prime)	B	B(prime)	C	C(prime)	D	D(prime)
Stretch	1.76	2.67	3.04	2.59	2.01	2.59	1.87	3.02
Bend	16.34	11.58	13.21	10.44	13.51	16.6	20.47	18.91
Stretch-Bend	0.733	0.97	1.23	0.81	0.71	0.71	0.76	0.92
Torsion	7.68	1.76	4.29	1.13	10.17	6.93	8.27	9.52
Non-1,4 VDW	-4.14	-0.43	1.22	-0.84	-2.98	-2.69	-3.19	-2.58
1,4 VDW	17.47	18.36	18.99	19.5	18.13	19.39	17.21	19.15
Charge/Dipole	-4.65	-7.28	-11.6	-13.7	-6.06	-3.1	-4.49	0.048
Dipole/Dipole	-0.96	5.29	4.65	5.98	-2.42	-0.88	-1.87	-0.72
MM2 Total energy	34.24	32.91	35.03	25.9	33.07	39.6	39.02	48.25
MOPAC PM6 Energy	-91.66	-77.51	-85.9393	-68.61	-91.66	-66.7	-88.71	-66.8

Structure A has the acetate group below the ring so it interacts from this side, meaning that the nucleophile attacks the oxonium ion intermediate from above. The MOPAC method determined the heat of formation of A and C to be exactly the same at -91.66 kcal/mol.

Meanwhile structure B has the acetate group above the ring, so in the next step the nucleophile attacks from the bottom – again, like for A and C, the heats for formation of B and D are very similar, within 2 kcal/mol of each other.

The reason for this similarity lies in the way that PM6 does its calculations: it views the molecule as a single unit, and finds its lowest energy by moving around electrons in the molecule until the optimal conformation is reached. The actual structure of the sugar is thus in between A and C, and in between B and D - a structure known as a cyclic dioxolenium ion . It is also worth noting the relative instability of C compared to C' (25kcal/mol) and D compared to D' (22kcal/mol). This is explained by the anomeric effect mentioned earlier, which favours the formation of axial α-anomers, even though equatorial β-anomers are normally preferred due to sterics. The anomeric effect is only significant when substituents are axial, so C and D gain stabilisation from this effect unlike C' and D'. It is worth noting that the stereoelectronic cause of the anomeric effect is the hyperconjugation of a lone pair on the anomeric oxygen with the antibonding σ* orbital of the C-O in the dioxolenium ion. This is only possible when the C-O is axial.

Miniproject: High stereoselectivity on low temperature Diels-Alder reactions

The Diels Alder reaction is a cycloaddition reaction between a conjugated diene and dienophile to form a substituted cyclohexene system and is considered one of the most beautiful reactions in organic chemistry due to its simultaneous simplicity and elegance. This was recognized in 1950 with the award of the Nobel Prize in Chemistry to its discoverers Otto Diels and Kurt Alder.

Today it remains one of the most powerful reactions possible in organic synthesis, particularly for obtaining polycyclic rings, due to the rapid accumulation of polyfunctionality and stereochemical control that it offers.

Normally the cycloaddition proceeds quite well by simply mixing the substrates, because the usual dienophiles have a carbonyl or equivalent group that, through conjugation, lower the energy of the LUMO antibonding pi orbital to an appropriate level for reaction with the diene HOMO.

However, in cycloenones this energy lowering is not enough to produce a reaction. This poses a problem, as cycloenones are very useful dienophiles in the synthesis of octalones and related bicyclic olefinic ketones, such as steroids.

To rectify this, Lewis Acids catalysts such as AlCl₃ can be used to enhance the reactivity of these poor dienophiles, and in the following investigation by da Silva Filho et al the stereoselectivity of the Diels Alder reaction of various 2-cycloenones with cyclopentadiene was measured with a niobium pentachloride (NbCl5) catalyst at different temperatures (fig.14).

Fig.14 Mechanism of the Diels Alder reaction of a 2-cycloenone with cyclopentadiene catalysed by niobium pentachloride

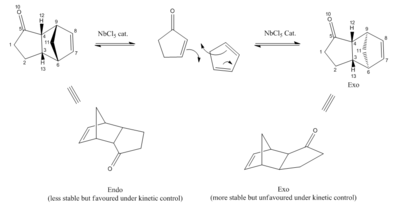
It was found that the corresponding endo and exo products were formed in a ratio depending on the reaction temperature – as expected, lower temperature resulted in higher selectivity as the reaction was then under kinetic control. In such conditions, the endo product is favoured due to an effect known as the endo rule which was explained earlier in this module using frontier molecular orbitals in the context of the dimerisation cyclopentadiene. Another more thorough explanation comes in the form of secondary orbitals.

Any reaction in which a kinetic effect dominates a thermodynamic effect on a reaction is usually explained based on the signs of the coefficients of the frontier orbitals. This is best illustrated using an example from literature (fig.15), which employs ψ2 of butadiene as the HOMO of the diene, and ψ3* of acrolein as the LUMO of the dienophile.

Fig.15 a)Illustration of primary and secondary orbital overlap b) in ortho adducts c) in meta adducts

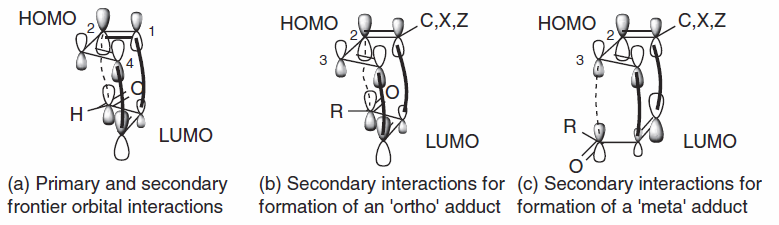
Placing these orbitals in the right places for the endo reaction, we can see the primary interaction explained earlier (solid bold lines ) with overlap of orbitals with matching signs. But there is also an additional bonding interaction (dashed lines) between the lower lobe of the p-orbital on C2 of the diene and the upper lobe on the carbonyl carbon of the dienophile as they too have the same sign. This interaction is called a secondary orbital interaction, and doesn’t result in a bond, but is likely to make a contribution to lowering the energy of this transition structure relative to that for the exo reaction, where it is be absent. Thus Alston suggested that regioselectivity in Diels-Alder reactions may be better attributed not to the primary interaction of C1 and C4, but to a secondary one, which is larger for the orbital on C2 (fig 15b) than with the smaller lobe on C3 (fig 15c), even though it is not forming a bond.

In this mini-project, I chose to test two hypotheses, namely that a) computational techniques are capable of confirming the structures of compounds found experimentally by characterising the two isomers formed in the reaction described above, and b) that DFT can distinguish between the isomers. The way I did this was to use computational chemistry to find properties of the molecules that can be found in wet labs, namely their NMR and IR spectra and optical rotation, and to compare this with the literature.

First, the molecules were drawn in chembio3D and optimized by MM2 and MOPAC/PM6 methods.

DFT was then used in the form of the mpw1pw91 functional and 6-31g basis set, and a spectrum was predicted in GaussView using the GIAO approach. GIAO stands for ‘gauge invariant atomic orbital’, and this approach was developed in the 1990s to deal with the fact that in more approximate schemes, the requirement for gauge invariance in not fulfilled, meaning that computationally predicted magnetic properties depend on the choice of the coordinate system

The jmol of the endo product can be found here, and the exo product is here The 13C NMR data found by DFT is compared to experimental data from the literature in table 6, and the spectra are shown in fig. 16 and 17.

Fig.16. The 13C NMR Spectrum of the endo product DOI:10042/to-11786

Fig.17. The 13C NMR Spectrum of the exo product DOI:10042/to-11776

Table 6: 13C NMR data for endo and exo products, with carbon assignments based on numbering in fig.14

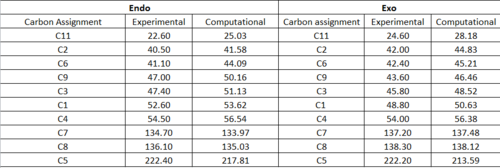
Happily, comparison of the two sets of data show an almost perfect match between the computational calculation of the 13C NMR spectra and the experimental one found by da Silva Filho et al - nearly all the expected chemical shifts are within 2-3 ppm of those obtained, suggesting that the first hypothesis of this mini-project is true. Further confirmation of this can be found in the IR spectra - data for this is in table 7 and figs 18 and 19.

Fig.18. The IR Spectrum of the endo product DOI:10042/to-11785

Fig.19. The IR Spectrum of the exo product DOI:10042/to-11784

Table 7: IR data for the exo and endo product

Inspection of the spectra reveals identical peaks for both the exo and endo isomers, with the endo product showing a higher absorption due to its greater prevalence as detailed in the explanation of the endo rule above.

Having confirmed the first hypothesis, our attention now shifts to the second one: Can computational techniques tell the difference between two isomers? The endo and exo products differ merely in the stereochemistry of the bridge (see fig. 14). I therefore chose to analyse the j-coupling constants of the geminal hydrogens on this bridge - according to theory these values should be different for the isomers, as was found in the literature. Computational techniques should provide similar results. The ¹H NMR spectra of both molecules are given in figures 20 and 21.

Fig.20. The 1H NMR Spectrum of the endo product DOI:10042/to-11786

Fig.21. The 1H NMR Spectrum of the exo productDOI:10042/to-11776

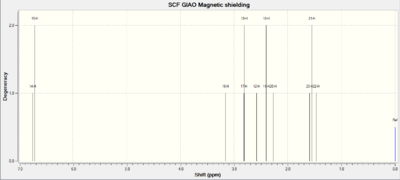This calculation was harder to approach than others because the software provided to analyse j-values, Janocchio, was found to give very inaccurate results. However, after many attempts, a new, more accurate method was found: The file that was orginally input into SCAN to calculate the NMR spectrum was edited to include the keywords 'NMR=SpinSpin' - this was then used by the Gaussian software to compute all the coupling constants for both the endo (DOI:10042/to-11778 ) and the exo (DOI:10042/to-11777 ) products. In both of the output files, the key coupling constants are the ones between atoms 22 and 23. The results are shown in table 8.

Table 8: Coupling constants for geminal hydrogens

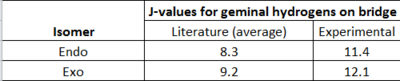
While the computational and experimental values do differ by about 3 Hz, there is a definite trend: the coupling constant of the geminal hydrogens on the bridge of the endo isomer is about 0.8 Hz less than that for the exo isomer. Thus the DFT method has been proven to provide a way of differentiating two isomers, confirming the second hypothesis of this mini-project.

As an 'after-thought', the optical rotation of the molecules was also calculated. Its values were deemed less important than the others described due to the fact that they are often calculated erroneously. For the record, the optical rotation of the endo product was found to be 196.7° (DOI:10042/to-11783 ), and for the exo product was found to be -83° (DOI:10042/to-11782 ). This is not necessarily a good or bad result, as these values would only be equal in magnitude and opposite in sign if the isomers in question were enantiomers, which they clearly are not.

---