Rep:Mod1:jc808

Molecule Mechanics Modelling

Molecular modelling has shown itself to be effective and reliable way to predict the physical properties of molecules and the outcome of reactions in silico. During the course of this module, the ChemBio and Gaussian suites will be employed to investigate the following problems:

The hydrogenation of a Cyclopentadiene dimer The stereochemistry of nucleophilic addition to two different pyridinium rings (NAD⁺ analogues The conformation/atropisomerism of a large ring ketone intermediate in one synthesis of the anti-cancer drug Taxol

The origins of the regioselectivity of the electrophilic carbenylation of a chloro-substituted bicyclic diene The use of DFT molecular orbital theory to investigate Neighbouring group participation (NGP) on the C-Cl and/or C=C stretching frequency of the above bicyclic diene A Mini-project investigating stereochemistry and spectroscopic simulation in an intermediate of the synthesis of Baclofen

Hydrogenation of Cyclopentadiene dimer

Dimerisation of Cyclopentadiene

Cyclopentadiene is observed to form homodimers at room temperature via a Diels-Alder cycloaddition. Two isomer could result from the thermal cycloaddition, the exo 1 and endo 2. At room temperature, the endo 2 is exclusively formed. this result can be investigated using Molecular Modelling.

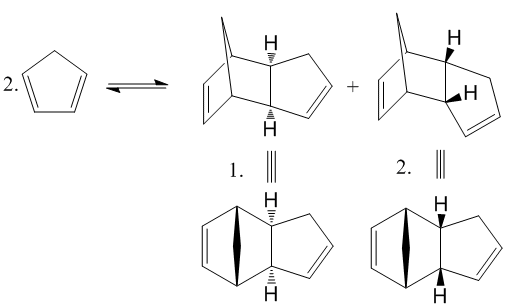
Fig. 1: dimerisation of cyclopentadiene

Analysis of the relative energies of each stereoisomer using the MM2 force field function of ChemBio3D yields the energy of the most stable geometry of each molecule.

The results are tabulated below:

Table 1: Cyclopentadiene dimer energies

Dimer	Energy / kcal mol-1	Energy / kJ mol-1
exo-dicyclopentadiene 1	31.9	133.5
endo-dicyclopentadiene 2	34.0	142.3

Dimer 1 has the geometry with the lowest energy and so must be the thermodynamic product. However, experimentally, the endo dimer 1 is the only isomer present at room temperature. This implies that the reaction is kinetically controlled and therefore, the endo configuration forms more rapidly. This can be explained by looking at the transition states.

It can also be concluded that the reaction must be irreversible at room temperature, otherwise the ratio of products would equilibrate, with the more stable endo product 1 dominating. At higher temperatures, 200-250°C, the thermal barrier can be surmounted and the exo product can be produced. It is known that tri-, tetra- and pentamers can be formed and have a lower energy, but the rate of formation is so much slower than dimerization that they do not normally exist.

The Hydrogenation of Cyclopentadiene Dimer

The kinetic dimer 2, as determined above, can be hydrogenated via the use of a palladium catalysts for example. Two possible dihydro derivatives are possible, 3 and 4.

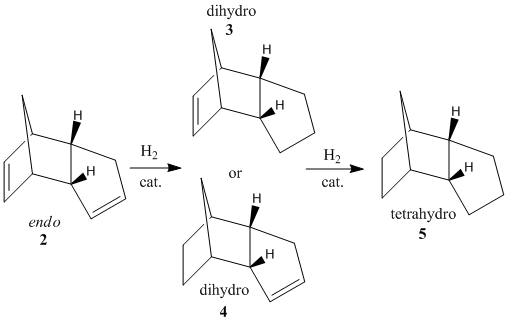
Fig. 2: hydrogenation products of dicyclopentadiene

Prolonged hydrogenation will result in the tetrahydro-derivative 5. The energy of each isomer was again analysed using MM2 in ChemBio3D.

Table 2: hydrogenation product energies

Hydrogenation Product	Stretching / kJ mol-1	Bending / kJ mol-1	Torsion / kJ mol-1	Van Der Waals / kJ mol-1	H-Bonding / kJ mol-1	Total energy / kJ mol-1
di-hydro product 3 dihydro3	5.37	83.2	45.2	23.6	0.678	149
di-hydro product 4 dihydro4	4.56	60.9	52.4	18.8	0.589	130
tetra-hydro product 5 tetrahydro5	4.64	54.0	71.2	25.5	NA	147

It can be seen that the greatest difference between the products lies with the bending strain. The greatest value is found for product 3. This is due to the fact that the double bond in product 3 is found on a norbornene-type ring. The bridging means that the ring cannot deform to adjust for the presence of the double bond, causing noticeable strain. This is not a problem for product 4 as the double bond is found on an un-bridged 5-membered ring, which can make small changes to it's geometry to lessen the strain. In fact, it is this norbornene strain on the double bond that causes the hydrogenation to take place here, at rates several times higher than at the cyclopentene ring. Therefore, product 4 is both the kinetic and thermodynamic product with a lower energy than that found in product 3. This observation is supported by a journal which found the same result through moleculat modelling. It is only with prolonged hydrogenation that the tetra-hydro product will be made.

The tetra-hydro product 5 has a very high torsional energy. Obviously, the rigidity of the double bond helps to hold the geometry and reduce unfavourable rotation about bonds. In fact, this high torsional energy raises the total energy to almost as high as the di-hydro product 3. The stretching, Van der Waals and H-bonding energies are all similar. As all three products are composed of the same atoms, this is to be expected. Note that there is a very small H-bonding value for the di-hydro products due to the possibility of a dipole being formed across the double bond. Of course this is not possible for the tetra-hydro product.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

Reaction of Pyridinium Ring in N-methyl Pyridoxazepinone 5 with Grignard Reagent

Two reactions on pyridinium rings will be investigated. The first involves the methylation of N-methyl pyridoxazepinone (prolinol) 5, using the Grignard reagent, methyl magnesium iodide. The reaction shows superior regio- and stereo-selectivity, up to 19:1 in favour of the below product. Note that the alternative regio-isomer would be attack on the carbon adjacent to the nitrogen on the pyridine ring. The cause of this is likely due to the presence and angle of the carbonyl with respect to the pyridinium ring. As Grignard reagents are known to coordinate to carbonyls before nucleophilic attack, the regio-selectivity is clear. The magnesium coordinates to the carbonyl oxygen and brings the nucleophilic methyl into close proximity to carbon 4 of the pyridinium ring.

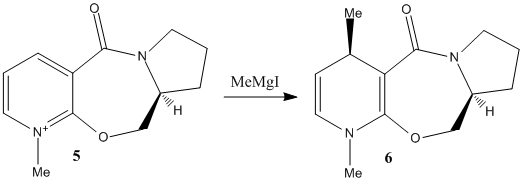
Fig. 3: methylation of prolinol 5 using a Grignard reagent

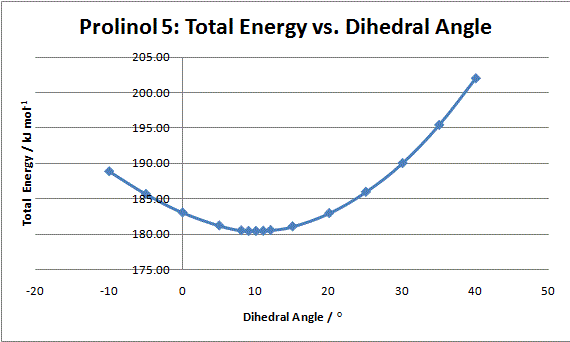
Graph 1: Total energy vs.dihedral angle between carbonyl and pyridinium ring of prolinol

The sterospecificity is most likely decided by the orientation of the carbonyl with respect to the aromatic ring. Using ChemBio3D, the dihedral angle can be set and the energy minimised using MM2. The angle with the lowest energy will therefore be the most stable geometry. The result are summarised in graph 1. It can be seen that an energy minimum lies around 10°. Further analysis around this angle shows 9° to be more precise. This means the carbonyl lies slightly out of the plane as shown in fig. 3. Once the magnesium of the Grignard reagent has complexed, the nucleophilic methyl lies slightly closer to the aromatic antibonding orbital. Electron tranfer results in the methyl adding to the top face of the ring (as shown) while the hydrogen moves to the underside.

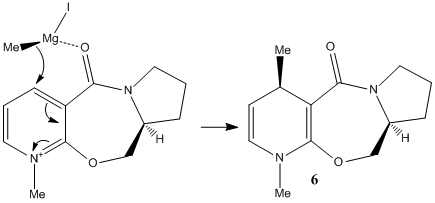
Fig. 4: orientation of nuclephilic methyl with respect to the pyridinium ring

Reaction of Aniline on Pydridinium Ring in N-methyl Quinolinium Salt 7

The second example involves the transfer of an NHPh group from aniline to carbon-4 of the pyridinium ring. A similar reaction conducted found a greater than 98% enantiomeric excess.

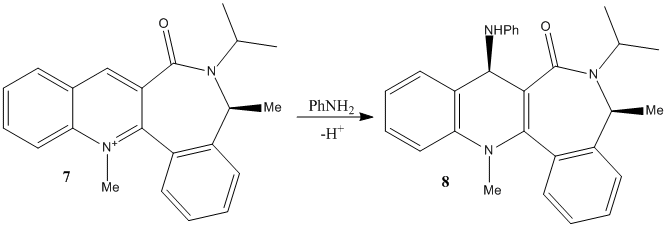
Fig. 5: Reaction of aniline and N-methyl Quinolinium Salt 7

By performing a similar analysis of the dihedral angles between the carbonyl oxygen and the pyridinium ring, the most stable geometry can be found.

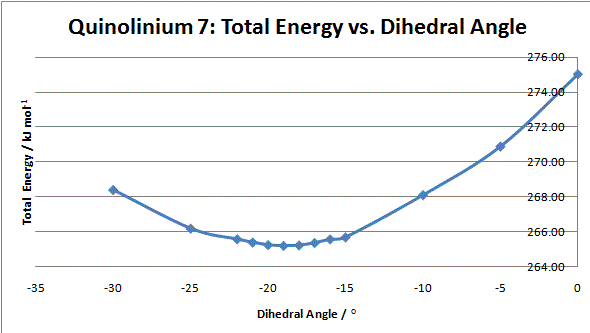
Graph 2: Total Energy vs. Dihedral Angle for N-methyl Quinolinium Salt 7

It can be seen that the optimum geometry is -19°, i.e. the carbonyl below the plane of the ring as shown. This means that it is sterically and electronically unfavourable for the aniline to approach from this direction. The top face of the ring is relatively unhindered and so the nitrogen approaches from this side and attacks via its lone pair. If the reaction taking place involved complexation, such as that seen for prolinol, the carbonyl would direct the nucleophile to the opposite face and the alternative enantiomer would be formed.

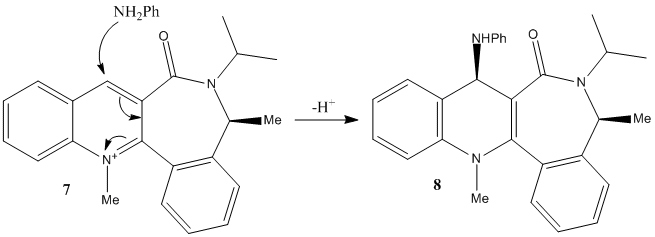
Fig. 6: Mechanism of the nucleophilic attack of aniline on N-methyl Quinolinium Salt 7

The loss of a proton completes the reaction.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Atropisomerism

Compounds 9 and 10 below are intermediates of the synthesis of the anti-ovarian cancer drug Taxol. The reaction creates both 9 and 10, but will isomerise to the most stable isomer. Which form this is can be found be using the MM2 function of ChemBio3D, to find the isomer with the lowest energy.

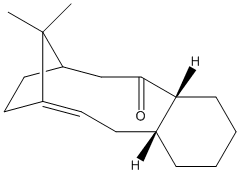Fig. 7: atropisomers of an intermediate of taxol

Table 3: Relative energies of isomers 9 and 10

Isomer	Stretching / kJ mol-1	Bending / kJ mol-1	Torsion / kJ mol-1	Van Der Waals / kJ mol-1	H-Bonding / kJ mol-1	Total energy / kJ mol-1
Isomer 9 taxol9	11.2	66.3	76.5	53.1	0.601	205
Isomer 10 taxol10	10.7	44.6	82.9	52.4	-0.755	185

It can be seen that the total energy of isomer 10 is lower than that of 9. The greatest difference is found for the bending energy, with isomer 10 being the lowest. This is likely due to the fact that the orientation of the carbonyl forces the decene ring in isomer 9 to be more removed from the ideal. Isomer 10 allows the decene ring to adopt a more favourable geometry. This is an example of atropisomerism. The flipping of the decene ring to the most stable conformer is hindered by the cyclohexane ring and the bridging propylene. This explains the observed result of the reaction products slowly adopting the conformation of isomer 10. As it is the most stable geometry it becomes the dominant product, but only after the energy barrier to rotation has been exceeded.

Hyperstable Alkenes

The taxol intermediates described above are observed to react very slowly with respect to the double bond. This can be explained by hyperstability. It is known that double bonds adjacent to bridging carbons are considerably less strained than the equivalent hydrocarbon. The stability is brought about by the fact that the bridgehead allows the olefin carbon to adopt the preferred 120° of an sp² carbon. A study conducted by Maier and Schleyer used an MM1 empirical force field program to confirm that bridged compounds with an adjacent alkene are considerably more stable than saturated equivalents. This stability imbues resistance to reaction and can be used to direct addition reaction to a certain double bond in a molecule.

Modelling Using Semi-empirical Molecular Orbital Theory - Regioselective Addition of Dichlorocarbene

Part 1: Molcular Orbital Analysis

The outcome of a reaction can be accurately modelled using semi-empirical Molecular Orbital Theory. The electrophilic attack of dichlorocarbene on the diene 12 will be directed at the double bond with the highest electron density in the Highest Occupied Molecular Orbital (HOMO). The electron pair in the double bond will attack the empty p orbital on the carbene. If the reaction studied was to be a nucleophilic attack, it would be the electron density of the Lowest Unoccupied Molecular Orbital (LUMO).

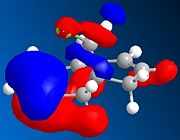
The relative energies of the molecular orbitals (MOs) can be calculated using the MOPAC function of ChemBio3D. For the following simulations, the PM6 method will be employed. Note that the alkene proximal to the chlorine atom will be described as the syn-alkene and the distal alkene called the anti-alkene

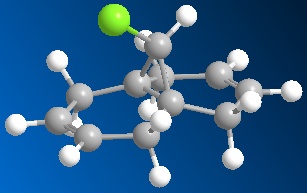Fig. 8: Compound 12

Table 4: Frontier orbitals of compound 12

HOMO-1	HOMO	LUMO	LUMO+1

It can be seen in the above MOs that the syn-alkene has the greatest electron density in the HOMO. As described above, the reaction proceeds via attack from the double bond into an empty p-orbital on the carbene. This means that the addition will take place at the syn-alkene. A similar study using PM3 calculations came to the same conclusion. This regio-specificity is so strong that a study by Halton and Russell was conducted exclusively to find a method of obtaining the anti-addition product.

Fig. 9: Electrophilic attack of dichlorocarbene by compound 12

Due to the steric bulk of the chlorine atoms, the carbene will likely approach from the underside of the molecule. This is also confirmed by the studies mentioned above.

Part 2: Vibrational Frequency Analysis

Structures for the diene 12 and the monoalkene 12a analogue (syn-double bond, fig. 10) were generated in ChemBio3D. The MM2 and PM6 optimised structures were imported into Guassian and set to run B3LYP/6-31G(d,p) opt freq. The saved .gjf file was submitted to the Chemistry Scan and the left to run over the weekend.

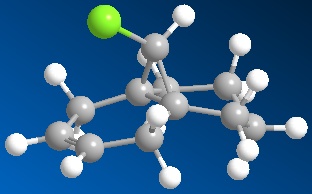
Fig. 10: monoalkene ananlogue

The Formatted Checkpoint Files were retrieved from the service and imported to Gaussian. This allowed the stretching frequencies of the various bonds to be analysed.

Table 5: Stretching modes of 12 and 12a

Compound	syn-double bond stretch / cm-1	anti-double bond stretch / cm-1	C-Cl stretch / cm-1
Diene 12	1757	1737	771
Alkene 12a	1758	-	775

It can be seen that the syn-alkene stretching energy is very similar in both compounds, the removal of the anti-double bond has little effect on it. This is most likely due to the bridging carbon found between the two rings. The rigidity conferred means that vibrations cannot effectively propagate past it and the two double bonds essentially vibrate independently.

The carbon-chlorine stretching frequencies are similar for both molecules. The chlorine is bound to the bridging carbon and so vibrations from the rest of the molecule will not affect it. The mass of the halogen also allows it to vibrate independently of the rest of the molecule. Note that the carbon-chlorine stretching vibration involves very little movement of the chlorine. Its mass means that it stays almost still while the bridging carbon is displaced.

Alkene stretching frequencies are usually found in the region 1630-1680 cm^-1. For reasons explained later in the report, this method of IR prediction usually overestimates the IR stretch by 8%. Adjusting for this brings the calcualated stretch down to 1627 cm^-1 for the syn-

and 1608 cm-1 for the anti-alkene. This brings it closer to expected values.

There is a significant difference between the two double bonds. The syn-double bond has vibration frequency 20cm^-1 higher than the anti. This implies that the anti- is a weaker bond, likely due to an inductive effect from the chlorine, and so the dichlorocarbene reaction would take place here. The previous MO analysis proved that the HOMO lies on the syn- and so these two results seem to counteract each other. However, even though the anti- double bond may be weaker, the electron density is found on the syn-double bond. The electrophilic addition of dichlorocarbene has little choice but to attack the syn-double bond. The computional study referenced earlier proposed that the attack occurs exclusively at the syn-alkene.

Structure based Mini project using DFT-based Molecular orbital methods

Enantioselective Michael Addition of Nitromethane to α,β-Enones Catalyzed by Chiral Quaternary Ammonium Salts

(R)-baclofen hydrochloride is a therapeutically useful GABA_B receptor agonist, making it effective against diseases as varied as spastic diplegia, multiple schlerosis, alcoholism and even hiccups. Both enantiomers are known to be active, but for most applications, the (R)-enantiomer has been found to be 100-1000 times more effective. A means of producing this enantiomer to a high enantiomeric excess has been widely investigated. One study by E. J. Corey and Fu-Yao Zhang devised a synthesis using chiral cinchoma ligands to afford high enantiomeric purity in an intermediate of 97.5:2.5 (after recryst.) in favour of the (R)-enantiomer, compound 6 in the scheme below.

Fig. 11: Reaction scheme for the synthesis of (R)-baclofen

The reaction of nitromethane with 4-chlorobenzylidineacetophenone 4 and the chiral cinchonium salt 5 with cesium flouride in toluene at -40°C gives Michael adduct 6 with R/S selectivity of 85:15 and 89% yield. Recrystallisation with ethyl acetate and hexane gave a 95% ee for the R-enantiomer. This enantiomerically purified compound can be oxidised to the ester 7, from which it is a simple process to reduce the nitro group with sodium borohydride. Note that the amine and ester will spontaneously react in a Michael addition to eliminate the phenoxy group. Hydrochloric acid is introduced to hydrolyse to amide and afford the target molcule (R)-baclofen hydrochloride 3.

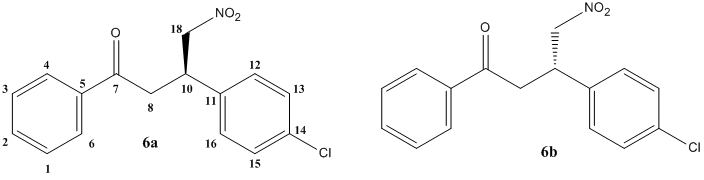
Fig. 12: (R)(6a) and (S)(6b) enantiomers of baclofen

The structure of each enantiomer was entered into ChemBio3D and the geometry minimised using the MM2 function. Several attempts were made to find the lowest energy by manual adjustment then re-minimisation. The lowest found was 47.98 kJ mol^-1 for the (R)-enantiomer and 41.64 kJ mol^-1 for the (S)-enantiomer. The molecules were saved as Gaussian input files set to minimise with the Method DFT=mpw1pw91 and the basis set 6-31G(d,p). The maximum number of cycles was limited to 25 to prevent meandering very close to convergence. These files were then uploaded to the SCAN suite.

¹³C NMR analysis

The ¹³C NMR of the product was given in the journal. This data will be compared to other literature values for both the (R),6a, and (S), 6b, enantiomers as well as the calculated values found through Molecular Modelling.

The optimised geometries for each enantiomer were re-uploaded to the SCAN suite to perform a NMR Chemical Shift calculation using the same method and basis set, using chloroform as the solvent.

Once complete, the file could be opened using Gaussian and the ¹³C NMR data analysed. Note that the reference was set to TMS mPW1PW9/6-31G(d,p) CDCl₃ GIAO as this was the solvent used in the journals.

(R)-enantiomer results: DOI:10042/to-7435 (S)-enantiomer results: DOI:10042/to-7434

Table 6: ¹³C NMR Chemical Shifts

Carbon Atom	(R)-baclofen 6a, Reported Shift / ppm	(R)-baclofen 6a, Literature Shift / ppm	(S)-baclofen 6b, Literature Shift / ppm	(R)-baclofen 6a, Calculated Shift / ppm	(S)-baclofen 6b, Calculated Shift / ppm
7	196.3	196.5	196.4	194.2 (198.7)	195.3 (199.7)
11	137.6	137.6	137.5	135.3	135.8
5	136.2	136.2	136.1	131.2	131.6
14	133.7	133.7	133.6	133.5	133.1
2	129.2	129.2	(not given)	130.8	130.7
13,15	129.0	129.2	129.2	126.0 and 125.9	125.5 and 125.4
12,16	128.9	128.9	128.8	127.0 and 124.5	128.4 and 127.8
1,3	128.8	128.7	128.7	125.2 and 125.1	125.1 and 124.9
4,6	128.0	128.0	127.9	126.0 and 125.6	125.7 and 125.5
18	79.5	79.3	79.3	78.2	74.2
10	41.5	41.3	41.3	41.9	41.2
8	38.9	38.7	38.6	40.8	40.0

The calculated shifts called for two adjustments to be made. Firstly, the carbon bound to the chlorine required a spin-orbit coupling correction to be made. This was achieved by subtracting 3ppm from the observed value. This brought to shifts for each isomer closer to the literature and reported value. Secondly, carbonyl carbons have been found to be incorrect by about 5ppm and so the formula δcorr = 0.96δcalc + 12.2 is recommended. However, this brings the corrected value (in brackets in the table) well above the observed value. This may be caused by secondary effects from the benzene ring or even the nitro group, so this correction was not implemented.

It can be seen that the correlation between the spectra reported by Corey and Zhang and that reported by Vakulya is high. Unfortunately, so is that found for the (S)-enantiomer by Kim and Huh. It appears that there is little difference between the magnetic properties of either structure. The spectral data for the (R)-enantiomer is confirmed by a study by Jiang, Zhang, Chan and Wang. An alternative spectrum for the S-enantiomer could not be found, so this cannot be confirmed.

However, the calculated NMR shifts for each molecule match quite well, except for carbons 8, 10 and 18. These carbons are on or adjacent to the stereocentre and so are likely to have the most varied electronic properties. For the literature spectra, the shifts for these carbons match very well, being identical in some case. This might signify that the molecule synthesised by Kim and Huh was in fact the R-enantiomer. But as stated above, another journal containing the S-enantiomer could not be found to prove this hypothesis.

The correlation between the calculated shifts and that found in literature was not exceptionally good. One discrepancy was as high as 5ppm (this carbon, 5, was located next to the carbonyl so perhaps this needed a similar correction). The remaining shifts generally had a difference of approximately 2ppm. Perhaps the fact that the molecule contains two aromatics as well as a carbonyl and a nitro group could have had acute effects on the electronic properties of the molecule and effected the SCAN. Alternatively, the fact that the connecting carbon chain and nitro group chain allows some conformationally flexibility, could mean that the geometry optimization wasn't accurate. The molecules were redrawn and the above procedure repeated to see if different results would be obtained. After experimentation, the minimum energies found this time were 46.58 and 47.81 kJ mol^-1 for the (R) and (S) enantiomers respectively. The NMR data was retrieved and summarised below:

(R)-enantiomer, geometry 2: DOI:10042/to-7437 (S)-enantiomer, geometry 2: DOI:10042/to-7436

Table 7: Repeated ¹³C NMR Chemical Shifts

Carbon Atom	(R)-baclofen 6a, Reported Shift / ppm	(R)-baclofen 6a, Literature Shift / ppm	(S)-baclofen 6b, Literature Shift / ppm	(R)-baclofen 6a repeat, Calculated Shift / ppm	(S)-baclofen 6b repeat, Calculated Shift / ppm
7	196.3	196.5	196.4	193.8 (198.2)	193.4 (197.8)
11	137.6	137.6	137.5	131.2	135.6
5	136.2	136.2	136.1	130.5	131.1
14	133.7	133.7	133.6	133.6	133.2
2	129.2	129.2	(not given)	130.5	130.9
13,15	129.0	129.2	129.2	125.8 and 125.9	125.7 and 125.4
12,16	128.9	128.9	128.8	127.4 and 124.5	128.4 and 124.1
1,3	128.8	128.7	128.7	125.2 and 125.1	124.9 and 124.1
4,6	128.0	128.0	127.9	127.1 and 126.0	125.7 and 125.7
18	79.5	79.3	79.3	79.4	79.0
10	41.5	41.3	41.3	43.5	39.9
8	38.9	38.7	38.6	41.8	41.9

It seems that in some cases the shifts are closer to those found in literature and in others, further away. I believe the problem lies in the flexibility afforded by the chain between the two aromatics. Looking at the returned optimised geometries, it is obvious that radically different structures are possible.

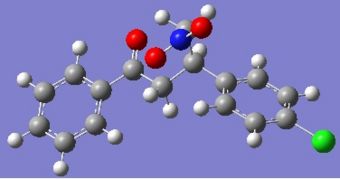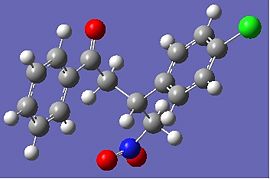Fig. 13: Geometry 1 and 2 of R-baclofen (above) and S-baclofen (below)

Even small differences in geometry can cause differences in calculated NMR, so it is no surprise they do not match literature values.

IR analysis

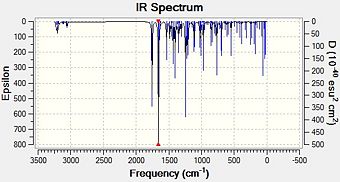
Due to the geometry problems outlined above, both calculated geometries will be submitted for IR analysis in the hope that one lies close to literature.

Using ChemBio3D, .gjf files were created for each of the four molecules being analysed. They were submitted to the SCAN procedure using # b3lyp/6-31G(d,p) opt freq as a method. Once complete, the spectra could be analysed using Gaussview.

Fig. 14:IR spectra for R-baclofen, geometry 1 and 2

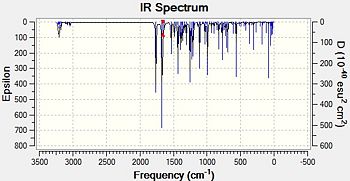Fig. 15:IR spectra for S-baclofen, geometry 1 and 2

The expected peaks are present. Firstly, those around and above 3000 cm^-1 are caused by C-H stretches, both aliphatic and aromatic. There are two very prominant peaks around 1660 cm^-1 and 1760 cm^-1 on all spetra. These must be due to the nitro and carbonyl groups on the molecule and looking at the animation provided. Nitro group asymmetric stretches usually show up in IR at around 1550 cm^-1, while ketones adjacent to aryl groups are approximately 1690 cm^-1. Obviously, the calculated spectra gives higher values than this. However, it is known that stretches are normally about 8% too high for these types of spectrum. Correcting for this gives values of:

Table 8: IR data (raw data in brackets)

Stretch	(R)-baclofen, Reported IR peak / cm-1	(S)-baclofen, Literature IR peak / cm-1	(R)-baclofen Geometry 1, Calculated IR peak / cm-1	(R)-baclofen Geometry 2, Calculated IR peak / cm-1	(S)-baclofen Geometry 1, Calculated IR peak / cm-1	(S)-baclofen Geometry 2, Calculated IR peak / cm-1
Nitro asymmetric	None given	1551	1536 (1659)	1542 (1665)	1542 (1665)	1546 (1670)
Carbonyl	1683	1684	1625 (1756)	1636 (1767)	1623 (1753)	1630 (1761)

The calculated nitro peaks are very close to that reported in the journal, giving peaks close to 1550 cm^-1. The carbonyl peaks are slightly further to literature values. This may be because of the fact that this stretch involves two N-O bonds vibrating and so the method of decreasing by 8% may not work. In fact, the literature and calculated values differ by 4%, which may reflect the stretching of two bonds. Decreasing each value by 4% gives 1688, 1699, 1686 and 1693 respectively, bringing them closer to the literature values.

Each geometry of an isomer gives similar calculated peaks, showing that the IR spectrum is not majorly affected by geometry. The nitro peak was not reported in the original journal, so a comparison cannot be made. A journal containing IR data for the (S)-enantiomer could not be found at all meaning it is not known if each enantiomer would produce different shifts. This lack of research reflects the relative pharmacological uselessness of the (S) enantiomer.

Optical Rotation

Literature sources give optical rotations of [α]_23D = +17.9 and [α]_25D = -10.8 for the (R) and (S) enantiomers respectively. This would have been a useful way to differentiate the isomers. However, the modelling method used is limited to only being able to accurately predict the optical rotations of molecules showing [|α|] > 50. Therefore, this is not applicable to the molecule being studied.

Conclusion

Molecular modelling using Guassian, ChemBio and the SCAN suites has proved to be useful in predicting and assigning the spectral data for organic compounds. For both ¹³C and IR spectra, the calcuations have returned figures that are at least similar to those found in literature. However, due to the fact that the molecule is not fully constrained means that baclofen has many geometries, each with similar energies but highly varied structures. Submitting, these differing geometries returned a range of results. Even so, the peaks and shifts gathered were accurate enough to prove that this method can at least confirm the structure of a molecule. A slight degree more constraint in the structure may allow more definitive identification.

The ¹³C literature values of each enantiomer were almost identical. This could mean that each enantiomer was so electronically similar that it is not suitable for this type of analysis. However, the calculated values I generated were close in both cases except for three key carbons, implying they are related to the isomerism. This could mean that the (S)-baclofen synthesised by Kim and Huh was in fact the (R). They achieved their synthesis with the use of a chiral cinchona catalyst, similar to Corey and Zhang, perhaps the outcome was not what they expected.

Overall, the concept of using molecular modelling to predict reaction and identify compound has been proven. Ideally, better choice of analyte should have been made. Firstly, one with a more constrained structure and secondly, one with more literature data available to compare against. Lack of time meant that a new molecule could not be found and analysed.