Rep:Mod1:fkl2010

Third Year Computational Organic Chemistry

Third Year Computational Organic Chemistry

Introduction

In the past decades, huge amount of money was spent on researching new molecules and reaction. Moreover, chemists are also interested in modifying and developing new catalysts and reaction scheme. When a new reaction scheme is proposed, it is essential to investigate whether the reaction could give the desired product and understand how the reactants react with each other.

By introducing molecular mechanics stimulation method, the structure of the product(s) and the mechanism can be predicted. This could make the research process to be much more efficient and could prevent any potential hazards when this reaction is to be performed in the laboratory.

Molecular Mechanics

In this section molecular mechanics is introduced. This is to describe the motion of the molecules using classical physics. The potential energy of the molecule will be calculated and is defined as the force fields. Here below shows an equation describing the energy contributed in the force fields in the molecular system.

E = E_bond + E_angle + E_dihedral + E_{electrostatic} + E _{van der Waals}

where

E_bond = bond stretching within the molecule

E_angle = the bond angle between the atoms in the molecule

E_dihedral = the dihedral (torsion) angle between the atoms

E_{electrostatic} = electrostatic force found between the atoms

E_vanderwaals = the van der waal interaction betweenthe atoms

Program Used in This Exercise

There are two types of stimulation method involved in this exercise: MM2 and MMFF94 found in ChemBio 3D Ultra. The former method is used to calculate the static energy of simple molecules and give the values that contributed to each of the energy terms. The later method contains a better set of atom types than MM2 is used when the structure of the molecule is more complex (e.g DNA, peptide chain…etc).

Aim of This Exercise

In this exercise, it is aimed to determine the minimum point of energy of the product and its conformations. As such the reaction mechanism and the reaction pathway could be visualized.

The Hydrogenation of Cyclopentadiene Dimer

Dimerisation of Cyclopentadiene

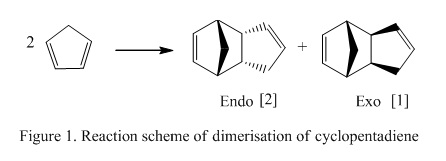
When cyclopentadiene is placed under room temperature, it will slowly react with itself to form a dimer known as dicyclopentadiene. It is an example of [4π + 2π ] (if referring to the number of π electrons in the system) or [3+2] (if referring to the number of atoms involved in the reaction) cycloaddition. As the electron count shows that there are 6 electrons involved in the reacting system. Therefore, the reaction is known to undergo Huckel transition and will also have a suprafacial arrangement. Note that sometimes, this reaction is also known as the Diels-Alder reaction. This reaction is known to be stereospecific and would generate two possible products: endo- and exo-. Endo product is formed when the bonds formed are on the top phase (i.e Hydrogen atoms) where exo product is formed when the bonds formed are on different phase.

The overall dimerization process and the proposed mechanism is shown in Figure 1 and 2 as below:

The energy of the endo and exo product was calculated and shown in Table 1 and the structure of the optimized geometry is shown below.

Exo Product

Endo Product

Table 1. Comparison between the energy of the endo and exo product

Product Conformation	Energy /kcal mol-1	Energy /kJ mol-1
Endo	34.00	142.47
Exo	31.81	133.29
Energy Difference between endo and exo product	2.19	9.18

The endo conformation is of a higher energy than the exo product. This showed that the formation of the endo product is less thermodynamically favorable and it is expected that the majority of the product found in the product mixture should be the exo conformer. However, Alder et al showed that the endo product exist as the major product. This shows that the reaction is under kinetically control.

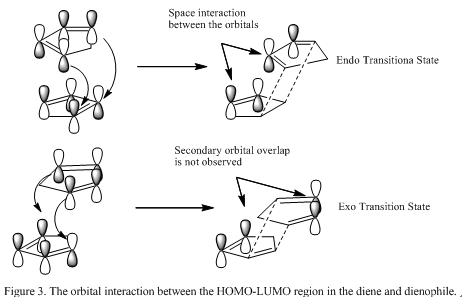
One of the approaches to understand the reason for the formation of the kinetically stable product is to consider the Transition State (TS) formed during the reaction using Endo rule. The endo rule stated that the TS is stable when there is a maximum overlapping between the diene and the substituents bonded to the double bond of the dienophile. Consider the endo TS, the substituents orientated towards the diene where the substituent in the exo TS orientated away from the diene. As such, stabilization between the substituent and the diene is achieved in the endo TS and the energy of the TS is lower. Hence, the endo product is formed.

Another way to understand formation of the endo product is to study the secondary orbital overlap (SOO) between the diene and the dienophile. In the endo TS, there is orbital overlap between the HOMO of the diene and the LUMO of the dienophile which further stabilizes the reaction. This interaction of orbitals is shown in Figure 3.

Pulling all the explanation together, it is found that the endo conformer is the major and kinetic product of this reaction where the exo product is the thermodynamic product due to the fact that it is less steric hindered. However, if the dimerization reaction is made to be irreversible, it is predicted that the exo conformers will be the major product due to the stability its geometry.

The Hydrogenation of Cyclopentadiene Dimer

By hydrogenating the endo product formed in the above section, there are two possible isomers, which is shown on the right and in Figure 4. The energies of the molecule is calculated and is shown in Table 2. Note that the ideal Sp ² hybridized angle = 120 DEG

Structure of molecule 3

Structure of molecule 4

Table 2. The energy contributions and their difference between molecule 3 and 4.

Type of Energy	Molecule 3 /kcal mol-1	Molecule 4 /kcal mol-1	Difference of Energy /kcal mol-1
Stretch	1.24	1.10	0.14
Bend	18.97	14.51	4.46
Stretch-Bend	-0.76	-0.55	-0.21
Torsion	12.15	12.50	-0.35
Non-1,4 VDW	-1.56	-1.51	-0.05
1,4 VDW	5.73	4.51	1.22
Dipole/dipole	0.16	0.14	0.02
Total Energy	35.93	31.51	22.42
H-C=C Bond Angle /DEG	127.1	124.4	N/A
H-C-C Bond Angle	112.4	110.4	N/A
C=C Bond Length	133.0	133.0	N/A

Consider the total energy of the molecules; it is found that the overall energy of molecule 4 is lower than molecule 3. This indicated that molecule 4 is more stable thermodynamically and is reckoned to be the major product in the hydrogenation. On the other hand, molecule 3 will result as the kinetic product and will form if the reaction is under kinetic control.

In order to show that molecule will be the major product in this reaction, it is intended to analyse the breakdown of the total energy and compare each of the energy in detail:

1. The energy of the endo product, molecule 2, was found to be 34.00 kcal mol^-1 in the previous section. From table 2, it is found that the energy of molecule 3 is higher than that of molecule 2 (i.e molecule 2 = 34.00 kcal mol^-1 and molecule 3 = 35.93 kcal mol^-1). Hence, the formation of molecule 3 is energetically unfavorable whereas there is a reduce in energy by forming molecule 4 (i.e molecule 2 = 34.00 kcal mol^-1 and molecule 4 = 31.51 kcal mol^-1, ΔE = -2.49 kcal mol^-1). This showed that by forming molecule 4, the energy barrier for the reaction will be lower and stabilize the structure.

2. The difference between the stretching energy for both molecule 3 and 4 is relatively small (i.e different by 0.14 kcal mol^-1). This indicates that the structures of the molecule are similar to the ideal bond length (i.e the bond length of C=C was found to be 133pm where the actual C=C bond length is 134pm)

3. The value and the difference of the Non-1,4 VDW energy (contributed from Hydrogen-Bonding) is relatively small compare to the rest of the energies found in the table. This is due the fact that there is not electronegative atoms presented in the molecule and hence, there is not much hydrogen bonding interaction.

4. The bending energy of molecule 3 is much higher than in molecule 4 (i.e ΔE = 18.69 kJ mol^-1). This showed that the structure of molecule 3 is relatively unstable with a large deviation of bond angles from the ideal molecule. Furthermore, by considering the position of the double bond in both molecules. The C=C bond is found closer to the bridging carbon in the norbornene in molecule 3 than in molecule 4. This showed that there is an increase in steric hinderance and strain in the molecule. As a result, the rotation of the bond is restricted and the increase in bending would lead to the relief of strain in the norbornene.

5. Finally, a comparison is made between the H-C=C and C-C=C bond angles found in the molecules, which is related to the above argument. The ideal angle for a sp² hybridized carbon should be about 120^o. Consider the H-C=C bond angle in molecule 3 and 4, which is 107.6^o and 112.5^o, it can be seen that the bond angle between molecule 3 is smaller than molecule 4, indicating that the strain found in molecule is larger than in molecule 4 and hence, the energy of molecule 4 would be relatively lower. On the other hand, consider the C-C=C bond angles found in both molecules, which are 112.4^o and 110.4^o respectively. This showed that the C-H bond formed after hydrogenation in molecule 4 is having an angle close to a sp³ centre (i.e 109.5^o) rather than molecule 3, indicating that molecule 4 is more stable.

Pulling all the facts together, it can be concluded that molecule 4 will dominant in the product mixture as the thermodynamic product whereas molecule 3 will be the kinetic product, which will be formed when the reaction is under kinetic control. In fact, this is prediction matches the experimental results reported by Shala et al which stated that hydrogenation would take place in the norbornene part of the molecule and is proceeded several times faster than the hydrogenation in the cyclopentene ring. The hydrogenation process is found to be exothermic as well (i.e -138.8 kJ mol^-1 for norbornene hydrogenation and -109.5 kJ mol^-1 for the hydrogenation of the cyclopentene ring. The reaction scheme for the further hydrogenation process is shown in Figure 5. Further calculation was done for the complete hydrogenated species, which is shown below labeled as molecule 4A. The energies are summarized and is shown in Table 3.

Structure of molecule 4A

Table 3. The energy contributions and their difference between molecule 4A and 4.

Type of Energy	Molecule 4A /kcal mol-1	Molecule 4 /kcal mol-1	Difference of Energy /kcal mol-1
Stretch	1.11	1.10	+0.01
Bend	12.90	14.51	1.61
Stretch-Bend	-0.48	-0.55	+0.07
Torsion	16.94	12.50	+4.44
Non-1,4 VDW	-1.29	-1.51	+0.22
1,4 VDW	6.08	4.51	+1.57
Total Energy	35.28	31.51	+3.77

From the table, it can be seen that molecule 4A is less thermodynamically stable than 4A. If the endo product, molecule 2, is to be hydrogenated to form molecule 4A, the energy barrier that needs to be overcome will be large (i.e different by +1.28 kcal mol^-1). There is also a significant increase in the 1,4 VDM energy, showing that as the number of hydrogen atoms add to the molecule increases, the strength of hydrogen bonding increases. As such, the formation of molecule 4A is energetically unfavourable.

Stereochemistry of Nucleophilic addition to a pyridinium ring (NAD⁺ analodue)

Reaction of Pyridinium Ring in Molecule 5 with Grignard Reagent

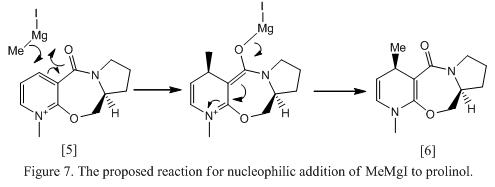
In this part of the exercise, two examples of nucleophilic addition reactions to a pyridinium ring are studied and their origin of stereocontrol in the formation of the products is investigated. As the structure of the molecule is getting more and more complex compared to the molecules studied in the previous section. It is therefore decided to use MMFF94 method instead of MM2 method as MMFF94 would provide better set of atom types than MM2.

The first reaction studies involves nucleophilic addition of MeMgI to prolinol, which the reaction scheme is shown in Figure 6. Note that MeMgI is not added to the structure during optimization as MMFF94 is used for investigating organic molecules. As Mg is an inorganic component, it could not be included in the structure. Addition of Mg would also increase the energy of the molecule, which would lead to a difficult optimization.

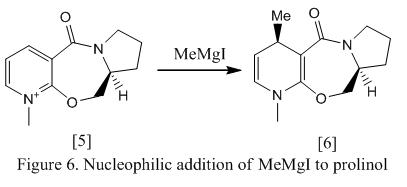
When the structure was first input for optimization, it was found that the C=O bounded in the 7-membered ring is lying above the ring (i.e having a positive dihedral angle). The structure was then alternated by moving the atoms in the molecule manually, for example, the oxygen atom in the 7-membered ring was moved below the plane of the ring where the neighbouring carbon atoms were moved above the plane of the ring. The structure was then re-optimised again. It turned out that the oxygen in the C=O bond was now lying below the plane of the ring (i.e having a negative O=C-C-C dihedral angle) with a different energy. Knowing that changing the orientation of the carbon and oxygen atoms would lead to different conformers with different values of dihedral angle, several stimulations were therefore run and the energies of the molecule were recorded for comparison purpose. The energies of the conformer are shown under Table 4.

Table 4. The energies and the dihedral angles of the conformers

Conformer	5a	5b	5c	5d
Carbonyl position w.r.t the C-H bond	Up	Down	Up	Up
Dihedral Angle (O=C-C-C)	18.1	-26.5	16.8	9.9
Energy/ kcal mol-1	57.48	59.05	57.40	57.46
Jmol	-			-

Table 4 shows that in most cases, the carbonyl group prefers to remain above the plane of the ring rather than below. The dihedral angle of most stable structure is found to be 16.8^o with a total energy of 57.40 kcal mol^-1. If the carbonyl group is placed below the plane of the ring, optimization will still succeed but lead to a higher energy complex. The structure of the most stable molecule with oxygen pointing above the plane (i.e 5c) and the structure with oxygen pointing below the ring (i.e 5b) is under Table 4 as well.

Knowing that conformer 5b is most stable and is favouable in formation, when MeMgI approaches the molecule, alkylation will occur in the same face as the oxygen atom in the carbonyl (i.e top face). The electron deficient Mg would attract to the electron rich amide oxygen, forming a 6 electron and magnesium enolate as transition state. This is known as chelate control.5 The mechanism of the reaction and the structure of the product, molecule 6, is shown in Figure 7 as below. The energy of the product is found to be -2.68 kcal mol^-1.

Molecule 6

Consider the structure of the product, it is believed that there will be steric effect contribute to the molecule. However, as the size of the methyl group is small, the steric hinderance effect will not be significant. Although molecule 6 appears to be the major product in the reaction, however, as this reaction is not 100% region- and stereo- specific, there will be chance for the formation of region-selective product (6A). This is shown in Figure 8.

In order to improve the selectivity of this reaction (i.e from 19:1 to >99:1), it is suggested to use Grignard with bulky R groups such as PhMgBr. This would improve the selectivity of the reaction (as indicated in figure 8). It is also worth knowing that alkyllithium reagents are not suitable for this reaction as this will result in region and stereorandom reaction.

Reaction of Pydridinium Ring in Molecule 7 with Aniline

The next part of the investigation based on a nucleophilic addition of aniline to a complex molecule, molecule 7, which contains a pyridinium ring. The structure of molecule 7 is shown in Figure 9.

During the stimulation process, It was found that like molecule 5, there were different points of minima found in molecule 7. In order to obtain the most stabilized structure (i.e with the lowest energy), several optimizations were run. The energies and the dihedral angles of the conformers are shown under Table 5 whereas the structure of the optimized can be viewed using jmol template.

Table 5. The energies and the dihedral angles of the conformers

Conformer	7a	7b	7c	7d
Carbonyl position w.r.t the C-H bond	Down	Down	Up	Down
Dihedral Angle (O=C-C-C)	-37.9	-40.6	53.7	-34.6
Energy/ kcal mol-1	98.46	101.67	130.03	101.71
Jmol

From Table 5, it is found that unlike molecule 5, the C=O lactam preferred to stay below the plane of the ring (i.e in most of the optimized structure, the carbonyl group is found to be below the plane of the ring). This can be explained by the fact that if the C=O bond lactam is placed above the plane of the ring, this will increase the steric repulsion between C=O and the adjacent methyl group. As a result, this will lead to a high energy molecule, which is thermodynamically unfavourable.

The chemistry is likely to occur if the C=O lactam is placed below the plane of the ring (i.e away from the external methyl group attached to the 7-membered ring). If a bulky aniline nucleophilie (due to the large size of Ph attached to the ring) approaches the molecule, the aniline will attacked the top face of the ring which is opposite to the C=O lactam to avoid steric repulsion between the large phenyl group and the carbonyl group.

Unlike the Grignard reagent used in the previous reaction, aniline does not contain any electropositive element (e.g Mg). As a result, there is no chelation effect observed between the amide oxygen and the nucleophile (i.e N), hence, an enolate transition state will be not observed. Instead, the lone pair on the nitrogen will attack the electrophilic carbon (carbon 4) in the pydinium ring and the PhNH- group is added syn to the methyl group attached to the 7-membered ring. In addition, another advantage of having aniline attacking the pydinium ring is that the repulsion between the lone pair on the nitrogen and the relatively negative oxygen in the carbonyl can be reduced. Leleu et al. showed that this reaction is highly stereoselective, giving a yield of >95%. The proposed reaction mechanism is shown under Figure 10.

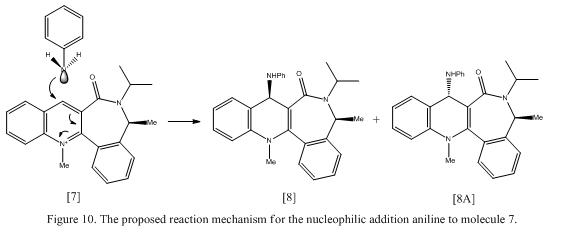
Although this reaction is highly stereospecific, there formation of product 8A is also possible. Calculations were done to compare the energy of the product. The energy of product 8 was found to be 60.11 kcal mol^-1. However, by changing the atoms in the molecule manually, the optimized structure was still found to have the oxygen atoms in the carbonyl group to be below the plane of the ring. This showed that the oxygen atom prefers to remains below the plane of the ring to avoid steric interaction. Note that this reaction has demonstrated atropenantioselectivity, which refers to the rotation motion of a single bond is inhibited due to high steric strain barrier.

Improvement of The Models used

Although molecular mechanics is able to predict the most stable conformation of the product, there are still rooms for improvement of the modeling system. Molecular mechanics stimulations use classical physics to predict the conformation and the properties of the product. In the previous experiment, the molecular mechanics methods used are MM2 and MMFF94 respectively. Each method contains a particular set of force field which contains equations that used to describe the potential energy of the molecule.

As each of the method contains a specific force field, only a certain types of molecules can be included in the calculation as the force field cannot be use for all type of different molecule with different character. In addition, the calculations preformed by molecular mechanics only depend on the interaction of the nuclei within the molecule and neglect the impact of the electrons in the molecule. As a result, if electronic effect plays a large role in a reaction (i.e bond making and bond breaking) or contribute to the property of the molecule, molecular mechanics method cannot be used.

In order to improve the modelling method, it is suggested to use electron structure method (e.g Density Function Method). This method uses the law of quantum mechanics in the calculation, which stated that the structure of the molecule, as well as its energy and properties can be obtained by solving the Schrodinger equation.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Taxol, also known as paclitaxel is a drug that used in cancer treatment. During the synthesizing process of Taxol, Paquette et al proposed that the imtermediates formed can be isomised to form atropisomerism. By definition, atropisomerisms are formed when the free rotation about the single bond is prohibited due to high steric repulsion between the neighbouring groups. As a result, the isomers can often be isolated and studied. The proposed intermediates and its conversion is shown in Figure 11.

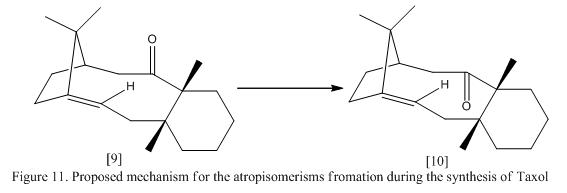
Chemistry will often occur in the carbonyl group as a carbonyl addition. Therefore, it is important to determine the lowest possible geometry of this isomer. In this exercise, molecular mechanics (MM2 and MMFF94) were used to optimize the intermediate in order to determine the most stable geometry. This orientation and the energies of the molecule are shown in Table 6 and the structure are shown using jmol in Table 6.

Table 6. Energy and orientation of carbonyl oxygen in the geometries

Computational Method	MM2	MM2	MM2	MM2	MMFF94	MMFF94	MMFF94	MMFF94
Molecule	9	9A*	10	10A*	9	9A*	10	10A*
Orientation of the carbonyl oxygen w.r.t the ring	Up	Orthogonal	Down	Down	Up	Orthogonal	Down	Down
Bend Energy/ kcal mol-1	16.43	17.09	12.91	11.27	N/A	N/A	N/A	N/A
Total Energy/ kcal mol-1	54.38	58.18	44.95	48.18	76.2	81.53	60.03	66.37
Energy Difference / kcal mol-1	9.35				16.7

• Note that 9A and 10A was found when the positions of the atoms were changed manually.

Molecule 9	Molecule 9A	Molecule 10	Molecule 10A
Molecule 9	Molecule9A	Molecule 10	Molecule 10A

From the table, it is found that both method generate the similar result, showing the same trend (i.e energy 9 > energy 10). Note that the energies produced by two methods were difference as different set of field was used.

Consider the optimized energies of the molecules, the energy of the molecule will be different if the hydrogen found in the C=C bond pointing up or down. The structure is more stable if both the C=O lactam and C-H bond found in alkene is pointing to the same direction. It is reckoned that the stability is achieved by having the carbonyl oxygen hydrogen bonded to the hydrogen atoms attached to the alkene group. Consider the conformer of the 6-membered ring in the intermediate, the structure of the ring tends to remain in the chair conformation rather than in the twisted boat structure. This will further stabilize the structure of the geometry. Notice that if the carbonyl lactam is placed orthogonal to the ring, the energy rises dramatically, this is due to the strain found in the C=O lactam. A normal Sp² hybridized molecule often has a bond angle of 120^o where in this molecule, the O=C-C angle was found to be about 116^o. To sum up the finding, it is found that molecule 10 is having the lowest energy and hence, if the intermediate [9] is generated in the reaction process, it will isomerize to intermediate [10] gradually such that reaction can be preceded further.

Reactivity of the Olefin found in the Intermediate

In order to determine the activity of the olefin, the Olefin Strain Energy (OSE) has to be taken into account. OSE refers to the energy difference between the olefin in the molecule and the parent hydrocarbon of itself. An alkene molecule always has a positive OS energy, indicated that it is susceptible towards reaction. By using the energy obtained, the stability and the reactivity of the olefins at the bridgehead can be determined. Maier et al showed that if the olefin is found at the bridgehead tends to have a negative OSE and less strain than its parent hydrocarbon and hence, the reactivity of the olefin reduced. If positional isomers are presented for this molecule, one would expected that the one with the olefin found at the bridgehead would be more thermodynamically stable.

It is first suspected that this stabilization is achieved by the increase in steric repulsion between the bridgehead and the olefin as well as the enhanced π-bond strength. However, Liebman et al proved that this stability is achieved by the cage structure of the olefin as well as the strain contributed from the parent cycloalkane found in the molecule.

Consider the structure of molecule 10, which contains a bridgehead olefin. It is therefore reckoned that the OSE will be negative with decrease in reactivity found in the double bond. This can be used to explain why the alkene reacts slowly and likely to resist to hydrogenation. As this type of alkene is stable towards hydrogenation and further attack, this type of alkenes are known as “hyperstable” alkene.

Modeling Using Semi-empirical Molecular Orbital Theory

Orbital Control of Reactivity

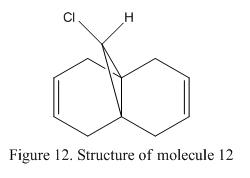
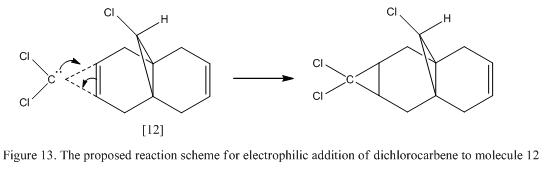
As discuss in the previous section that one of the limitations of using molecular mechanics to analysis the geometry of the molecule is that the impact of the electrons have during the reaction is neglected. Hence, if the endo stereoselectivity is about to be examined in Diels Alder reaction, this method is no longer useful. Figure 12 shows the structure of molecule 12. If dichlorocarbene is added to compound 12, a cyclic product will formed via electrophilic addition. This reaction process involves movement of the electrons between the molecules. In order to study this reaction more in depth, a better method is needed.

Molecule 12

The chemistry of reactions always occurs between the HOMO-LUMO region of a molecule as this is where the valence orbitals and electrons are found and is available for bond formation and breakage. In the other words the reactivity of the molecule is controlled by the orbitals in the HUMO-LUMO region. In this case, it is intended to compute the HOMO-LUMO in molecule 12. By studying these orbitals, the regioselectivity of this electrophilic addition (or similar types of reactions) can be evaluated.

Two molecule mechanics methods are involved in this stimulation process; MM2 and PM6. It is known that MM2 method will not include electronic interactions during optimisation. However, it is a relatively inexpensive computational method and can be used to generate the optimised structure in the first stage. Stimulations are then run using PM6 method, which will include valence-electron molecular wavefunction during optimisation. This will allow the HOMO-LUMO orbitals to be visualised for further analysis.

The structure of molecule 12 (which is also known as (9-ChIoro-1,4,5,8- tetrahydro-4a, 8a-methanonaphthaIene) is shown in Figure 12. It contains two C=C double bond in the molecule and is susceptible towards electrophilic addition. As there are two possible positions for addition reaction to occur, therefore, the interaction of the orbitals and as well as the stabilizing effect achieved have to be considered. Halton et al showed that electrophlic addition will mainly occur on the the π-face syn to the chloride (i.e C=C that is close to the Cl^-). This is mainly due to the stabilization effect achieved by the C-Cl σ* orbital and the anti π-orbital in the ring as well as some steric efffects. Therefore, if molecule 12 is reacted against dichlorocarbene, the addition of the CCl₂ molecule will be found along the endo side of the molecule. This is illustrated in Figure 13.

In order to further analysis the interaction of the orbitals, the HOMOs and LUMO of molecule 12 are generated. This is shown below.

LUMO +2	LUMO +1	LUMO	HOMO	HUMO -1

From the figure, it can be seen that the LUMO shows that the electron density around the anti-alkene where a high electron density is found around syn-alkene in the HOMO and HOMO-1. This shows that the syn-alkene is more nucleophilc relative to the anti-alkene. As a result, the syn-alkene is more susceptible for electrophilic addition.

Moreover, consider the shape and the structure of HOMO-1 and LUMO+1, it is realized that these two orbitals are having a similar shape and structure. Therefore, there will be antiperiplanar overlapping between LUMO+1 (i.e the C-Cl σ^* orbital) and HOMO-1. This will further stabilize the orbital. As such, the anti-alkene (i.e the exo π-orbital) is stabilized and is less likely to be attacked by the electrophile. One would expected that there will be overlapping effect between HOMO and LUMO +1 as the orbitals have similar shape and orientation. However, this is not the case, Halton et al showed that if this overlapping would occur, the resulting orbitals will be 0.08eV less stabile than the interaction between HOMO-1 and LUMO.

They have also preformed calculations on the p_π-orbital coefficient on each side of the alkene. It was found that the coefficient for the syn and anti alkene was 0.58 and 0.54 respectively. Hence, the HOMO-1 is known to be a more delocalized orbital and the syn-alkene will likely to be attacked first in an electrophilic addition.

Vibration Frequency

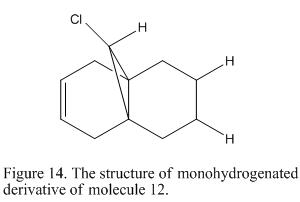
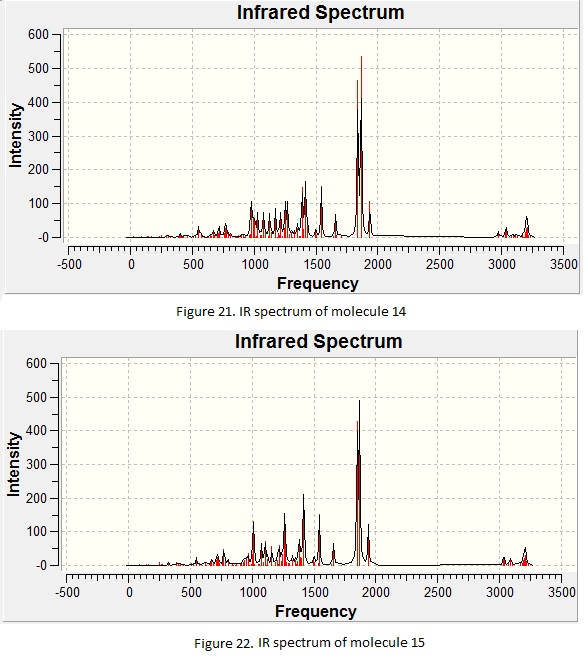
Molecule 12 is able to undergo hydrogenation to form molecule 13. In the previous section, it is found that there will be antiperiplanar overlapping between LUMO+1 (i.e the C-Cl σ^* orbital) and HOMO-1. It is reckoned that this overlapping would change the strength of the bond. In order to investigate the strength of the C=C and C-Cl bond found in the molecule, a frequency analysis was carried out and its stretching frequency is calculated and record as shown in Table 7 and 8 for both molecule 12 and 13. An infrared spectrum is generated for each molecule. This is shown under Figure 15 where the structure of molecule 13 is shown in Figure 14.

Molecule 13

Table 7. The bond stretching frequencies found in molecule 12

Types of bond	Frequency /cm-1	Infrared Intensity
C-Cl	770.80	25.14
Syn C=C	1757.44	3.94
Anti C=C	1737.01	4.19

Table 8. The bond stretching frequencies found in molecule 13

Types of bond	Frequency /cm-1	Infrared Intensity
C-Cl	774.94	20.02
Syn C=C	1758.05	4.34

Compare with the literature of the stretching frequency of C-Cl bond (740 - 780^-1), this shows that the computational results made a good agreement with the experimental results. The C-Cl bond length is found to be 770.08 and 774.94cm^-1 for molecule 12 and 13 respectively, showing that the C-Cl bond in molecule 12 is shorter than in molecule 13 and hence, the C-Cl bond in molecule 12 is much stronger. The intensity decreases as the molecule undergoes mono-hydrogenation. This is due to the fact that the anti-periplanar stabilization effect is no longer exists after hydrogenation.

The literature value of a C=C bond stretching frequency is found to be 1630 – 1680 cm^-1. However, the computational stretching frequency are found to be 1757.44 and 1758.05 cm^-1 respectively, which is higher than expected. Again, this is due to the anti-periplanar stabilization effect. Notice that the syn-alkene is having a higher frequency than the anti-alkene, this provide evidence that that the C=C bond energy must be higher and electrophilic addition should occur in the syn-alkene instead. This is not in the actual case because the frequency calculated is depended on the σ and π found in the molecule. However, only π bonding electrons are involved during the electrophilic addition process.

These results can be illustrated graphically using Figure 19. It can be seen clearly that the intensity of the C-Cl peak at about 780cm^-1 decreases once the anti π-orbital disappear upon hydrogenation. This observations also valid for describing the change in intensity of the C=C bonds as well. As molecule 13 is the mono-hydrogenated product, there is only one C=C presented in the molecule. Hence, only one C=C stretching band is found on the spectrum.

Structure Based Mini Project using DFT-based Molecular Orbital Methods

Optimisation of the Proposed Products from the Reaction

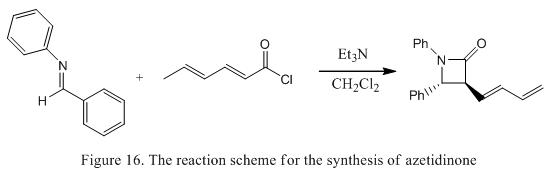
Azetidinone is a heteroaromatic organic compound with contains a four membered ring with a nitrogen atom. The azetidinone compounds are useful as they can be used as an inhibitor of cholesterol absorption and as a tool for characterizing the protein that helps to absorb cholesterol in the body. There are various methods of synthesizing azetidinone. One of which is illustrated in Figure 16.

In this mini-project, it is intended to investigate the reaction between azetidinone and maleic anhydride using toluene as solvent, which is an example of [4π + 2π] Diels-Alder reaction. The proposed reaction scheme and mechanism is shown in Figure 17 and 18 respectively.

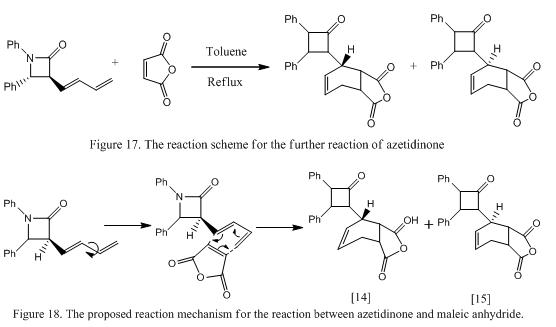
Sharma et al reported that in this reaction two distereoisomers will exist in the product mixture (labeled as 14 and 15) at a ratio of 2:1. Clearly, one would expected that molecule 14 should have a more stable geometry. In order to prove this observation, computational methods are used to minimized the energy and calculated the expected NMR and IR spectra and to compare with the literature results. The structure of molecule 14 and 15 is minimized and is shown below respectively. The energies and the dihedral angles of the stererisomers formed are shown in Table 9. Note that molecule 14A was found when the positions of the atoms were changed manually.

Table 9. The energies and conformation of molecule 14, 14A and 15

Molecule	14	14A	15
Orientation of the H atom on C3	Down	Down	Up
Orientation of H atom of 6-membered ring	Up	Up	Down
Orientation of the 6-membered ring w.r.t azetidinone	Up	Up	Down
Dihedral Angle of H-C-C-H between the azetidinone and 6-membered ring	-179.2	-168.1	164.6
Total Energy /kcal mol-1	61.57	63.65	61.87
Energy difference between molecule 14 and 15 /kcal mol-1	0.3

The structure of the product proposed by Sharma et al showed that the phenyl group adjacent to the nitrogen atom in the azetidinone is “pointing down” (i.e into the plane of the screen). Therefore, it is reckoned that the small hydrogen atoms found adjacent to this phenyl group will be pointing down to avoid steric interaction between the phenyl group and the large bulky group found in the 3 position. Compare with the computational results obtained, it was found that results stimulated matches well with the prediction. With the hydrogen atom pointing down, the overall energy of the molecule is smaller than with the hydrogen atom pointing up. Notice that if the hydrogen is to point up in the structure, the energy of the complex will increase. Also, the dihedral angle measurement shows that the bulky group will not align exactly 180^o with the hydrogen atom. This provides evidence that the molecule tries to avoid direct interaction with the neighbouring phenyl group.

However, the hydrogen atom that is attached to the phenyl ring will have the same orientation as the ring (i.e if the ring points down, the hydrogen attached to the ring points down too) as this would produce the most stable geometry. If not, there is likely to be repulsion effect observed with the C2-H.

Note that the structure has been optimised twice. This was because in the first optimisation, the maximum cycle was set to be 25. However, as the size of molecule is relatively large such that the there was error occurring in the file with the line “optimisation limit exceed”. In order to generate a fully optimised structure, the number of cycle used was changed to 40. By changing the number of cycle, the optimisation was able to complete with the most stable geometry obtained.

¹³C NMR Prediction of the Diastereoisomers Products

The ¹³C NMR spectrum can be predicted using DFT via GIAO approach. The ¹³C NMR spectrum for molecule 14 calculated and is shown in Figure 19a. The numbering system of the molecule is shown under Figure 19b. The NMR shifts obtained from the computational calculation are compared with the literature values and is shown under Table 10. A graph has been drawn to show the difference between the computational and experimental results. This is shown under Figure 19c.

Table 10. Comparison between experimental and computational NMR shifts for molecule 14

Carbon Number	Arbitary Carbon Number	Chemical Shift (Computational) /ppm	Chemical Shift (Experimental) /ppm	Difference between computational and experimental values /ppm
21	1	28	24.7	+3.3
18	2	39.8	36.4	+3.4
22	3	43.0	40.5	+2.5
23	4	45.2	42.9	+2.3
3	5	60.2	59.1	+1.1
2	6	62.4	61.1	+1.3
10	7	110.9	117.0	-6.1
6	8	115.7	124.1	-8.4
8	9	119.4	124.2	-4.8
16	10	121.5	126.1	-4.6
14	11	124.1	126.2	-2.1
9	12	125.0	128.6	-3.6
12	13	125.2	128.8	-3.6
13	14	125.5	128.9	-3.4
7	15	125.9	129.1	-3.2
11	16	126.1	129.4	-3.3
20	17	128.2	130.4	-2.2
19	18	130.4	130.6	-0.2
5	19	134.3	136.7	-2.4
15	20	134.6	137.0	-2.4
4	21	161.6	165.9	-4.3
24	22	171.2	171.1	+0.1
26	23	172.1	174.0	-1.9

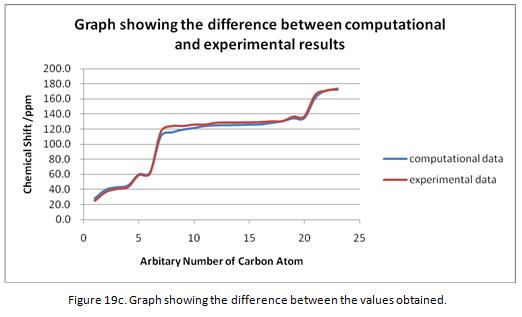
From the table, it can be seen that the computational and the experimental results are similar with a difference no more than 10ppm. This showed a good correlation. However, the computational NMR predicted tends to underestimate the chemical shift. It is reckoned that this is due the method used in the computational process. It was found that if the other basis set are used (e.g aug-cc-pvtz instead of 6-31G(d,p)), this would result in different values in the chemical shift. In general, by using computational methods, the relative position of the peaks can be defined. However, the method of the calculation has to be taken into account. The NMR spectrum of molecule 15 was generated using the same method. The spectrum is shown under Figure 20a where the numbering system of the carbon atoms is shown in 20b. The comparison between the experimental and computational results is made and is shown in Table 11.

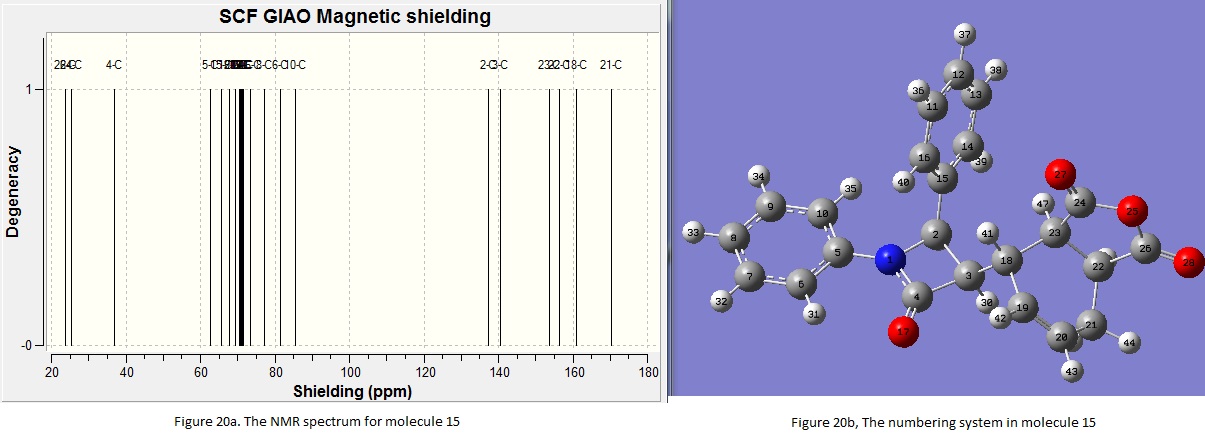
Table 11. Comparison between experimental and computational NMR shifts for molecule 15

Carbon Number	Arbitary Carbon Number	Chemical Shift (Computational) /ppm	Chemical Shift (Experimental) /ppm	Difference between computational and experimental values /ppm
21	1	26.1	24.2	+1.9
18	2	35.6	35.6	0.0
22	3	40.2	40.2	0.0
23	4	42.9	42.7	+0.2
3	5	56.0	59.3	-3.3
2	6	59.2	60.1	-0.9
10	7	111.0	117.0	-6.0
6	8	115.1	121.4	-9.0
8	9	119.3	124.2	-4.9
16	10	123.2	126.1	-2.9
9	11	125.0	126.2	-1.2
14	12	125.3	128.6	-3.3
12	13	125.6	128.8	-3.2
13	14	125.5	128.9	-3.1
7	15	125.9	129.1	-3.2
11	16	126.2	129.2	-3.0
20	17	127.2	129.4	-2.2
19	18	128.9	129.8	-0.9
15	19	130.9	130.6	+0.3
5	20	134.0	137.3	-3.3
4	21	159.7	165.9	-6.2
24	22	171.2	171.1	+0.1
26	23	172.7	173.7	-1.0

The results can be illustrated graphically; this is shown in Figure 20c. Again, from both the table and graph, it can be seen that the difference between the predicted values and the experimental values are fairy similar with the difference of chemical shift no more than 10 ppm. The same trend of prediction is observed: the computational method tends to underestimate the value of the actual chemical shift. This might have due to the computational method used during the simulation. Also, notice 27 peaks are identified in the literature where there is only 23 peaks identified in the computational process (there are 23 carbon atoms found in the molecule only). This may due to the overlapping of the peaks during the stimulation or unexpected splitting peaks found during the experimental process. Hence, this is recognized as one of the limitations of using computational method, which cannot be able to generate an identical NMR spectrum as the one obtained in the actual experiment. The NMR spectrum for both molecules are shown in here:

NMR for molecule 14: DOI:10042/to-5674

NMR for molecule 15: DOI:10042/to-5673

IR Analysis

The IR spectra for both molecules are stimulated. The stretching frequency identified from the computed IR spectrum is shown in Table 10 where the computed IR spectrum for molecule 14 and 15 are shown in Figure 21 and 22 respectively. Notice that both diastereoisomers give the same IR spectrum with same frequency as the type of bondings found in the molecule is the same. However, the intensities of the peaks are not the identical to each other. This is due to the change in dipole moments in the molecules which give arise to this difference. The major peaks are identified and compared to the experimental values. This is shown under Table 12.

Table 12. Comparison between the computed and experimental frequencies.

Types of bond	Computationan frequency /cm-1	Experimental frequency-1	Difference (computational-experimental) /cm-1
C=O bond stretching	1849	1770	+79
Aromatic C=C bond stretching (6-membered ring attached to C3)	1722	1739	-17
Aromatic C=C bond stretching (Phenyl ring attached to N)	1543	1596	-53
Aromatic C=C bond stretching (Phenyl ring attached to C2)	1498	1497	+1

Only four IR frequencies are reported by the literature. Although Table 10 showed that the difference between the predicted and actual frequency is differ by 100cm^-1 (maximum), however, the bond stretching frequency is still within the range (e.g the possible range for C=O bond stretching is 1670 – 1820cm^-1). This showed that the computed results are still reliable for prediction. The sum of free electronic and thermal free energies is compared between the two isomers. The free energy for molecule 14 and 15 are found to be -1243.28 and -1243.25 Hartrees, which is differ by 18.8kcal mol^-1. From the free energy obtained, it is found that molecule 14 has a more negative value than molecule 15. This showed that molecule 14 is more stable. According to the literature, it was found that the molecule 14 dominates in the product mixture. This showed that the computational method produces an accurate prediction. Notice that Diels-Alder reaction often produces the kinetic product (due to secondary orbital stabilization). In this case, both computational and experimental results showed that molecule 14 is formed. This indicates that this reaction is under thermodynamic control.

Conclusion

By using MM2, PM6 in ChemBio3D and Gaussian, the geometry with the lowest possible energy can be determined. By using the structure optimized, the properties of the molecules can be determined such as the free energy of the molecule, its NMR and IR spectrum. One would predicted that the NMR and IR spectrum may not look similar to the experimental results as obviously there might be errors occurring in the actual experiment and the parameters used in predicting the spectrum might be different to the actual parameters used. However, it turns out that the computation results matches quite well with the experimental result. Hence, it is possible to use these methods to predict the experimental outcome before carrying out the actual experiment in the future. In order to improve the computational results (i.e making the results more accurate compared to the experimental ones), it is suggested that to use a better basis set, for example B3LYP 6-311G (d,p). This could improve the accuracy of the prediction.