Rep:Mod1:david90
Module 1
David Freeman
The Hydrogenation of Cyclopentadiene Dimer
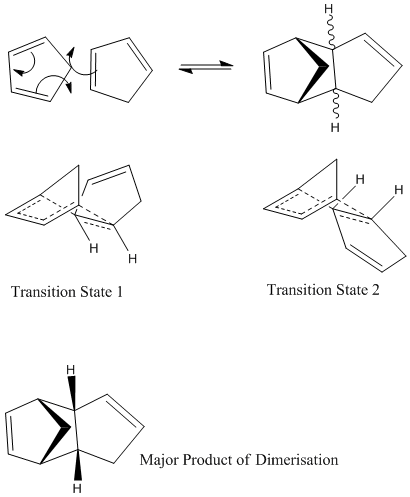
Molecules 1 and 2 were drawn using ChemBio3D and the minimum energy of each isomer found using the MM2 force field option. The energies found were:
1: 31.8812kcal/mol
2: 34.0017kcal/mol
The endo dimer will therefore be the predicted major product of the dimerization of cyclopentadiene since it is thermodynamically more stable. Experimentally isomer 2 is formed suggesting that kinetics have a larger effect than thermodynamics in this case. The Diels-Alder mechanism leaving the predicted isomer is shown below with the transition states of 1 and 2 as well as a picture of 2, the kinetic product.
Looking at the transition states shows why 2 is formed rather than 1, even though 1 is more stable. The transition state of 2 is much less sterically hindered than that of 1 meaning it will form much faster, resulting in 2 being the major product of dimerisation.
The same process was then performed on 3 and 4:
3:
Stretch: 1.2778 Bend: 19.8520 Stretch-Bend: -0.8347 Torsion: 10.8187 Non-1,4 VDW: -1.2249 1,4 VDW: 5.6398 Dipole/Dipole: 0.1621
Total Energy: 35.6907 kcal/mol
4:
Stretch: 1.0982 Bend: 14.5418 Stretch-Bend: -0.5478 Torsion: 12.5071 Non-1,4 VDW: -1.0766 1,4 VDW: 4.5011 Dipole/Dipole: 0.1407
Total Energy: 31.1643kcal/mol
The energy profiles show that 4 is the more themodynamically stable molecule and would be the result of monohydrogenation. It should be noted that the total energy of 3 is actually more than the dimer 2, meaning hydrogenation at this alkene is unlikely compared to the much lower energy molecule 4. Most of the energy in 3 comes from bending. This means that the bond angles in this conformation are further away from the natural angles than in conformer 4. The bond angle of the double bond around the ring in 3 was calculated using ChemBio3D and was found to be 108o, far from the ideal 120o. These very strained angles appear at either end of the bond, and both contribute to the high bend energy of molecule 3. The bond angles of the double bond around the ring in 4 are 112o and 113o, clearly much closer to the ideal which results in a lower bend energy. There is still a significant contribution to the overall energy from bending however, as the ring systems force the bond angles between carbons to be smaller than 109.5o which is the ideal for sp3 hybridized carbon.
A further minimisation was performed on the completely hydrogenated form which gave the following energy profile.
Stretch: 1.1215 Bend: 13.0004 Stretch-Bend: -0.4831 Torsion: 16.8784 Non-1,4 VDW: -1.3033 1,4 VDW: 6.0757
Total Energy: 35.2896 kcal/mol
This is slightly more stable than 3, but much less stable than 4. For this is the reason it is easy to hydrogenise the first alkene but the totally hydrogenated molecule forms only after prolonged hydrogenation.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
Molecules 5 and 6
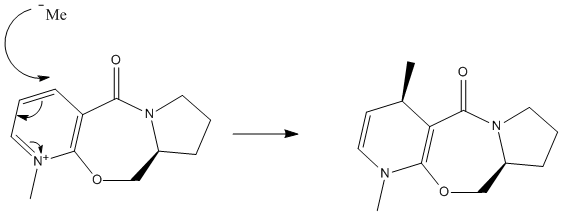
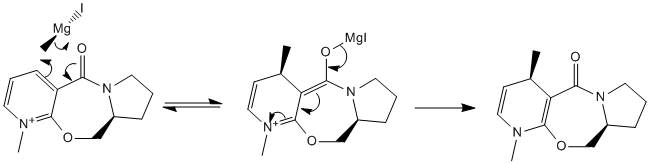
MeMgI cannot be used in the first example because Mg is unknown to the programme. This is unfortunate as (as discussed later) the Grignard actually forms a complex with molecule 5 to give the product and it would have been interesting to see the difference in energy between the starting material, the product and this intermediate.
Molecule 3 was drawn and minimized. Total energy was found to be 43.0843kcal/mol. Components of the rings were then moved to different starting positions and the molecule again minimized to try and find a lower energy configuration. Initially looking at the product suggests that the methyl nucleophile will likely attack from above. This suggests that the carbonyl group will be angled downwards (this turned out to be incorrect but was initially taken as a starting hypothesis) so as to create steric problems when attacking from below. This was taken as a starting point when looking for the lowest energy configuration. A proposed mechanism assuming the carbonyl is angled downwards in 5 is shown below.
The two total energies and torsion angles of the carbonyl to the pyridinium rings of the lowest energy minimisations of the molecule are shown below.
43.0678kcal/mol angle = 11
43.0550kcal/mol angle = 9
These two minimisations have the carbonyl group above the ring. It was in fact found that there was no configuration in which the carbonyl was angled downwards due to the rigidity of the ring systems, meaning the mechanism above must be wrong and another must be proposed. If the magnesium were to coordinate to the carbonyl oxygen then the methyl would then only be able to attack from above (since this is where the carbonyl oxygen is) and would give the product 6. This agrees with the literature[1]. A revised mechanism is shown below.
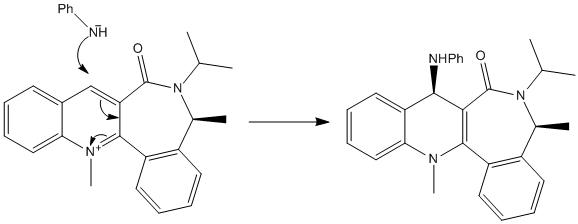
Molecules 7 and 8
At first glance this seems to be a very similar reaction to that above which suggests a similar mechanism. However, looking at the reactant (NH2Ph) shows that there is no way for it to coordinate to the carbonyl as Mg could, in fact the nucleophillic nitrogen would be repelled by the lime pairs on the oxygen atom. This means in this case the carbonyl must be on the opposite face to that which is attacked, namely the carbonyl must be pointing downwards so as to repel nucleophiles as well as causing steric hindrance. The mechanism must therefore be:
The MM2 minimisation was used and conformers with the carbonyl group both up and down were found. The details of the lowest energy conformers are shown below.
Stretch: 4.0345 Bend: 11.8641 Stretch-Bend: 0.4068 Torsion: 9.3072 Non-1,4 VDW: 3.4829 1,4 VDW: 29.4140 Charge/Dipole: 9.0703 Dipole/Dipole: -4.8987
Total Energy: 62.6811 kcal/mol angle = -19 (carbonyl below ring)
Stretch: 3.8676 Bend: 11.4637 Stretch-Bend: 0.4003 Torsion: 10.4438 Non-1,4 VDW: 3.8576 1,4 VDW: 29.3467 Charge/Dipole: 9.0402 Dipole/Dipole: -4.8793
Total Energy: 63.5406 kcal/mol angle = 21 (carbonyl above ring)
The total energies of the two conformers suggest, as expected, that the conformer with the carbonyl pointing downwards is the most stable. This supports the theory that the lone pairs on the carbonyl oxygen repel the attacking nucleophile and cause addition to the top face.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
The two atropisomers were drawn and minimized using MM2. Both are shown below in jmol applications with the relevant energy data. The most stable isomer will be the one that is formed on standing by the other isomer so it will therefore be this that reacts further in the formation of taxol.
Carbonyl group down
Stretch: 2.4988 Bend: 12.8527 Stretch-Bend: 0.2886 Torsion: 17.6687 Non-1,4 VDW: -0.7518 1,4 VDW: 12.1406 Dipole/Dipole: 0.2600
Total Energy: 44.9576 kcal/mol
Originally the structure minimised with the cyclohexane ring in the boat formation which gave a slightly higher energy. This was changed to the chair formation to give the result above. A jmol image has been included to show how the carbonyl is pointing below the ring in this molecule.
The atoms were then moved around to give the alternative isomer in which the carbonyl is above the ring. This was then minimised using the same techniques as above.
Carbonyl group up
Stretch: 2.9539 Bend: 18.9616 Stretch-Bend: 0.2552 Torsion: 18.7343 Non-1,4 VDW: -0.0635 1,4 VDW: 13.6713 Dipole/Dipole: 0.0639
Total Energy: 54.5767 kcal/mol
The most stable isomer using the MM2 force field was isomer 10 with the carbonyl group pointing downwards.
Using the MMFF94 minimisation showed that isomer 9 had an energy of Final Energy: 82.7857 kcal/mol and isomer 10 had an energy of Final Energy: 61.0339 kcal/mol. This is the same result as the MM2 force field and means that the predominant form of the taxol intermediate is that in which the carbonyl is angled downwards.
The alkene in this molecule reacts slowly because it is hyperstable[2]. Hyperstability occurs when the olefin strain energy is negative. In most alkenes this is positive but in the example above the interactions between hydrogens on the alkene (1,3 effect or gecko effect) lower the overall energy of the double bond, stabilizing it. It should be noted however that although the olefin strain energy is lowered, the corresponding alkane is still thermodynamically more stable (ΔH(alkene) - ΔH(alkane)>0)
Modelling Using Semi-empirical Molecular Orbital Theory
Molecule 12 was drawn in ChemBio3D and minimized using the MM2 force field. The results are shown below.
Stretch: 0.6129 Bend: 4.8462 Stretch-Bend: 0.0415 Torsion: 7.5971 Non-1,4 VDW: -1.0849 1,4 VDW: 5.7885 Dipole/Dipole: 0.1113
Total Energy: 17.9126 kcal/mol
The molecule was then further minimised using the MOPAC/PM6 force field.
Mopac Job: AUX PM6 CHARGE=0 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09750 (< 0.10000) Heat of Formation = 19.74037 Kcal/Mol
The molecule is shown below and the HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 are shown below that.
 |
 |
 |
 |
 |
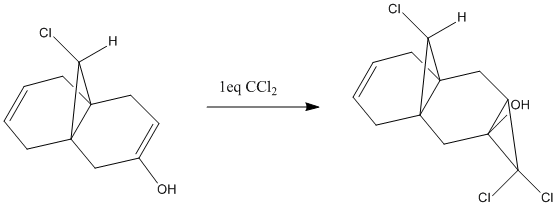
The HOMO of molecule 12 has electron density at the cis alkene, indicating that this would be the alkene to nucleophillically attack the dicholorcarbene. This is backed up by the literature[3]. A mechanism is shown below. The next highest occupied molecular orbital (HOMO-1) has electron density at the other double bond, meaning this is likely to react with a second dichlorocarbene, again nucleophillically attacking it. Looking at the LUMO+1 orbital shows that this orbital and the HOMO-1 may mix, raising the energy of the LUMO+1 but lowering the energy of the HOMO-1[3]. In this way the sigma* orbital of the C-Cl bond stablisises the pi orbital of the C=C and makes it less reactive to electrophiles such as carbenes, with the result that the cis alkene is the one to react.
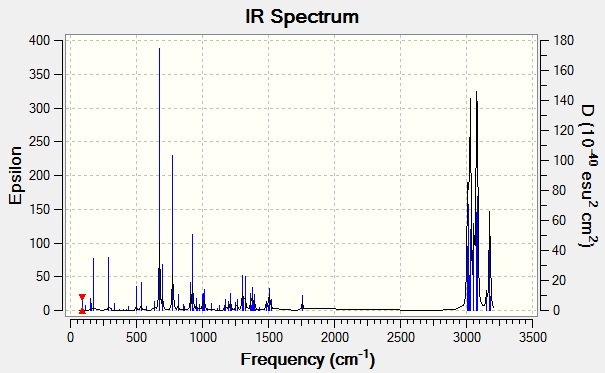
The stabilisation of the trans alkene means that it will have a lower bond energy than the cis alkene. This can be seen in the IR spectrum where the vibrational wavenumber for the cis bond is higher for the cis than for that of the trans. A higher wavenumber means a higher energy (E = hc/λ where 1/λ is the wavenumber), indicating that the cis bond will be more labile to electrophillic attack.
The density functional approach was used to find the vibrations of molecule 12, the predicted IR spectra is shown below with an assignment of the relevant peaks below that.
Main peaks:
| Wavenumber | Intensity | Bend/Stretch |
|---|---|---|
| 772.62 | 25.2742 | C-Cl stretch |
| 1740.88 | 4.1535 | anti C=C stretch |
| 1760.99 | 3.9050 | cis C=C stretch |
| 3000+ | various | various C-H stretch |
The literature[4] reports the frequency of vibration of a C-Cl bond as 785-540cm-1, which agrees with the calculated result. The literature value for an alkene stretch is 1690-1630cm-1. Both values of the calculated alkenes are too high. This could be because of two reasons, the calculation uses a harmonic approximation which assumes the bonds and atoms to act as springs and solid spheres. This is not like the real molecules which are anharmonic and not ideal. The second reason could be the chosen basis set. The basis set used was 6-31G and is a medium level basis set. If a higher degree of accuracy is required then a larger basis set is needed. This would dramatically increase computational time however.
As expected the cis bond frequency is higher than that of the trans. This agrees with the evidence given above with regards to the molecular orbitals.
The trans-monohydrogenated form of 12 was then analysed.
An MM2 minimisation was run for the trans-monohydrogenated molecule shown below.
Stretch: 0.8985 Bend: 4.7226 Stretch-Bend: 0.0156 Torsion: 10.7422 Non-1,4 VDW: -1.0538 1,4 VDW: 6.9473 Dipole/Dipole: 0.0709
Total Energy: 22.3432 kcal/mol
which was then subjected to a MOPAC minimisation:
Mopac Job: AUX PM6 CHARGE=0 EF GNORM=0.100 GRAPH SHIFT=80 Finished @ RMS Gradient = 0.08565 (< 0.10000) Heat of Formation = -2.43076 Kcal/Mol
The HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 are shown below for the monohydrogenated molecule.
 |
 |
 |
 |
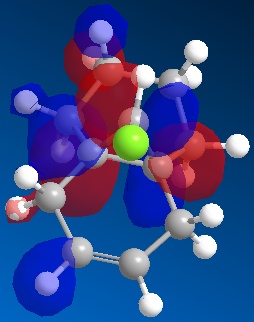 |
The LUMO is now the molecular orbital comprised mainly of the C-Cl sigma* orbital. This orbital is lower in energy than it's equivalent in 12 because it can no longer mix with the alkene orbital. This means the bond energy will not be raised for the C-Cl bond.
An IR spectrum was calculated for comparison with 12.
Main peaks:
| Wavenumber | Intensity | Bend/Stretch |
|---|---|---|
| 774.95 | 29.4751 | C-Cl stretch |
| 1758.05 | 4.3358 | cis C=C stretch |
| 3000+ | various | various C-H stretch |
Again the HOMO shows that the alkene is likely to be electrophillically attacked as this is where most of the electron density is. The frequency of the bond is similar to that of the cis bond in molecule 12 indicating the bond strength has not been largely changed by the loss of the other alkene.
The same procedure was run again using molecule 12 with OH on the anti alkene to analyse the effects of adding an electron withdrawing group. The oxygen will remove electron density from the alkene bond, increasing the energy of the bond. This will raise the wavenumber of the anti alkene.
Bend: 5.5975 Stretch-Bend: 0.0302 Torsion: 7.5922 Non-1,4 VDW: -1.4785 1,4 VDW: 5.5534 Dipole/Dipole: -0.0767
Total Energy: 17.8294 kcal/mol
Mopac Job: AUX PM6 CHARGE=0 EF GNORM=0.100 GRAPH SHIFT=80 Finished @ RMS Gradient = 0.08512 (< 0.10000) Heat of Formation = -27.01251 Kcal/Mol
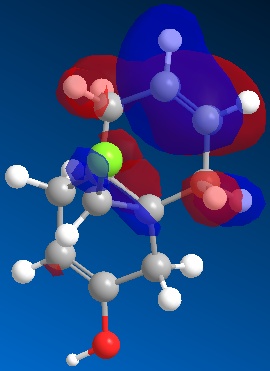 |
 |
 |
 |
 |
The HOMO in this case has electron density on the anti alkene, opposite to that of molecule 12. The bond has been destablised by the alcohol and is now higher in energy than the cis alkene. This will obviously mean the site of electrophillic attack by dicholorocarbene has changed to the anti alkene. The reaction scheme is shown below.
Main peaks:
| Frequency | Intensity | Bend/Stretch |
|---|---|---|
| 766.78 | 10.4226 | C-Cl stretch |
| 1756.28 | 4.8891 | cis C=C stretch |
| 1776.59 | 34.1913 | anti C=C stretch |
| 3000+ | various | various C-H stretch |
The IR data shows that the anti C=C bond orbital has indeed increased in energy. This was expected as it is now attached to an electron withdrawing group. The cis bond is similar to the other molecules, as can be seen in the diagrams the orbital that makes up this bond doesn't interact much with the substituents that have been changed.
Structure based Mini project using DFT-based Molecular orbital methods
The literature I have chosen to base my mini project on is:
A β-Lactam-Based Stereoselective Access to β,γ-Dihydroxy α-Amino Acid-Derived Peptides with Either α,β-Like or Unlike Configurations
Claudio Palomo, Mikel Oiarbide, Aitor Landa, Aitor Esnal and Anthony Linden[5]
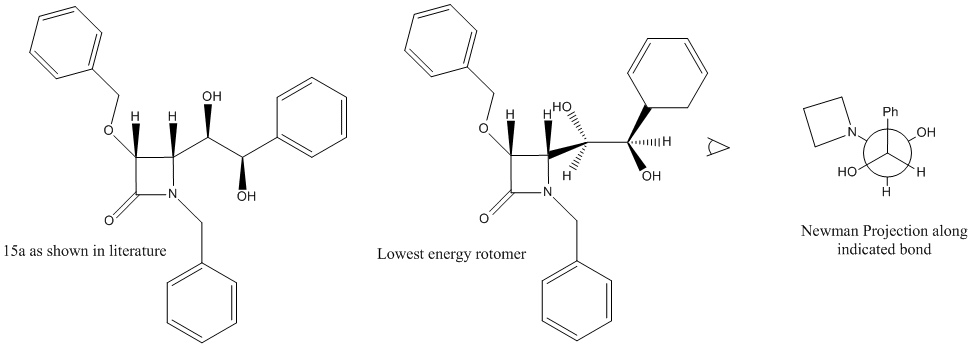
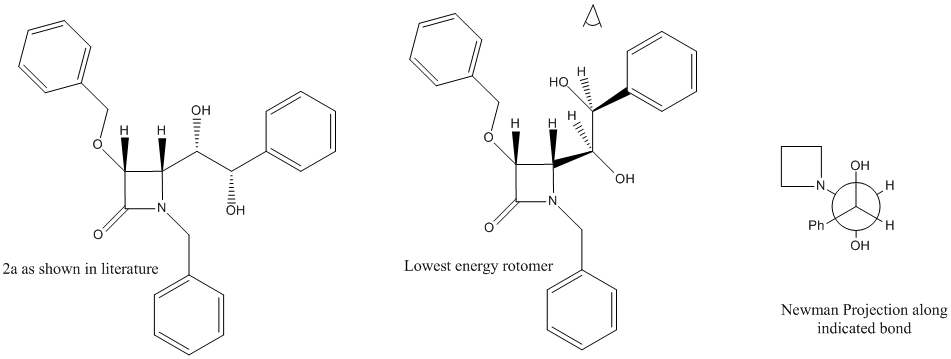
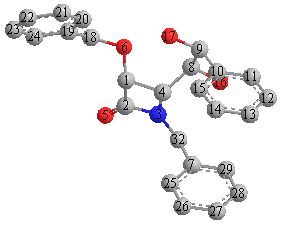
The specific part I will be focusing on is under scheme 4, the osmium catalysed dihydroxylation of 3a into the regioisomers 15a and 2a. It took some time to find the correct conformers of both 2a and 15a due to the rotation about two of the bonds. The structures were drawn and minimized using MM2 to find the lowest energy conformers with the help of drawn newman projections. There are 9 possible rotomers for each molecule if both bonds are rotated, each was tried and the two conformers of lowest energy are shown below in jmol applications.
For 15a the lowest energy was 45.7224kcal/mol and was found to be that in which the alcohol groups are antiperiplanar to each other.
Stretch: 3.6026 Bend: 42.1186 Stretch-Bend: -0.8053 Torsion: -7.4132 Non-1,4 VDW: -10.8515 1,4 VDW: 23.2032 Dipole/Dipole: -4.1320
Total Energy: 45.7224 kcal/mol
A MOPAC/PM6 minimisation was then run before the molecule was submitted to SCAN.
Mopac Interface ------------
Model: checkpoint_29547.fchk
Mopac Job: AUX PM6 CHARGE=0 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.08524 (< 0.10000) Heat of Formation = -78.57857 Kcal/Mol
For 2a the lowest energy conformer had an energy of 47.6799 kcal/mol and was also one of the rotomers in which the alcohol groups were antiperiplaner.
Stretch: 3.4859 Bend: 41.6460 Stretch-Bend: -0.7457 Torsion: -6.3981 Non-1,4 VDW: -13.1165 1,4 VDW: 23.3244 Dipole/Dipole: -0.5162
Total Energy: 47.6799 kcal/mol
Mopac Interface ------------
Model: Mod 1 miniproject 2a
Mopac Job: AUX PM6 CHARGE=0 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09052 (< 0.10000) Heat of Formation = -78.37620 Kcal/Mol
The literature reports that flash column chromatography was used to separate the isomers and their structures determined by X-ray crystallography. This would clearly be the best method, IR would give the same spectra for both isomers and NMR is also likely to give similar results.
MM2 minimizations were then run on two different molecules, 15a(Ph) and 2a(Ph) in which the benzyl group attached to the nitrogen has been swapped for a phenyl group. Drawings of both molecules are shown below.
15a(Ph)
Stretch: 2.5651 Bend: 36.8068 Stretch-Bend: -0.3961 Torsion: -5.5161 Non-1,4 VDW: -16.6072 1,4 VDW: 24.0178 Dipole/Dipole: -7.3788
Total Energy: 33.4915 kcal/mol
2a(Ph)
Stretch: 1.2753 Bend: 19.9190 Stretch-Bend: -0.8336 Torsion: 10.7651 Non-1,4 VDW: -1.2295 1,4 VDW: 5.6411 Dipole/Dipole: 0.1621
Total Energy: 35.6996 kcal/mol
The total energies of the two molecules are lower than that of their benzyl equivalents.
C13 NMR Analysis
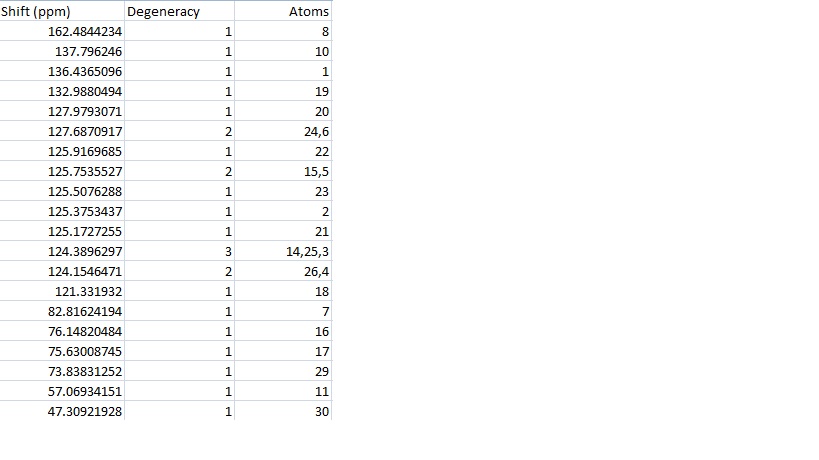
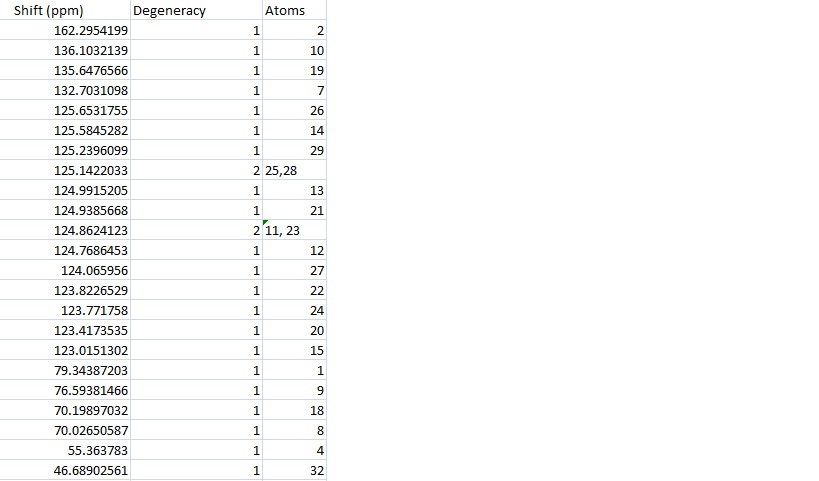
Both isomers were submitted to SCAN and their NMR data calculated. The calculated data for 15a was put into excel and is shown in the table, the carbon numbers are shown in the diagram.
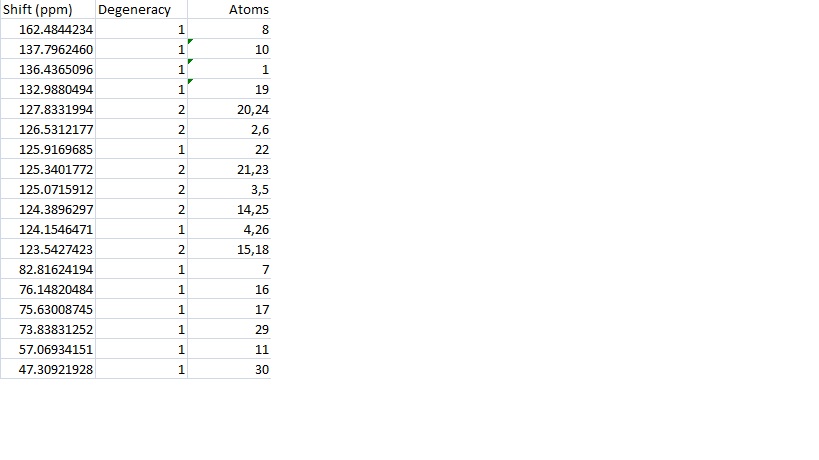
Looking at the data reveals that there are 21 peaks in the calculated data and only 18 in the literature. There are 19 individual carbon environments in the molecule. The calculation takes each carbon separately so has more peaks while the literature only has an accuracy of 1dp so two similar environments have been reported as the same. Since the atoms are labelled in ChemDraw it is possible to average the peaks given for atoms in the same environment however this may not be a good approximation because the calculation can't take this into account at all and reports only the shifts for a static molecule. This was done to give 19 calculated peaks and then two peaks were found that were equal to 1dp and averaged to give 18 peaks.
The peaks that were combined have the following corresponding carbon atoms and averaged frequencies:
| Atoms | Averaged Shift |
|---|---|
| 2,6 | 126.5312177 |
| 3,5 | 125.0715912 |
| 14,25 | 124.3896297 |
| 15,18 | 123.5427424 |
| 21,23 | 125.3401772 |
| 20,24 | 127.8331994 |
This seemed to be a good approximation as all the combined sets seemed to be made up of two very similar peaks (14 and 25 are actually the same peak anyway). This was the case for all apart from 15 and 18 which had shifts of 125.7535527ppm and 121.3319320ppm respectively. The two peaks that were found to be equal to 1dp were 4 and 26 which actually gave the same peak anyway at 125.8352606ppm.
Combined peaks
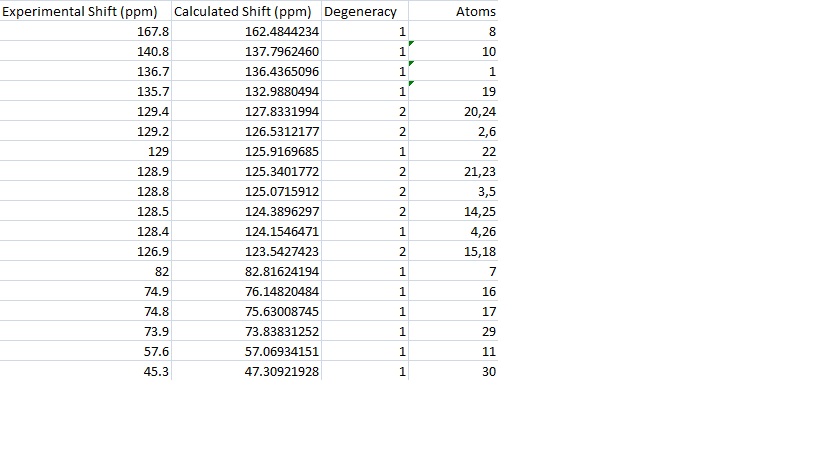
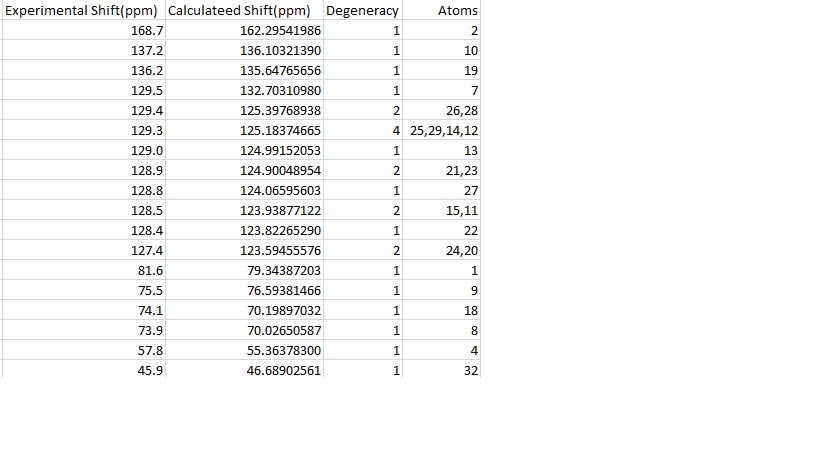
These peaks are shown again in the table below with their corresponding experimental peaks. The differences in these results were then calculated and have been shown graphically.
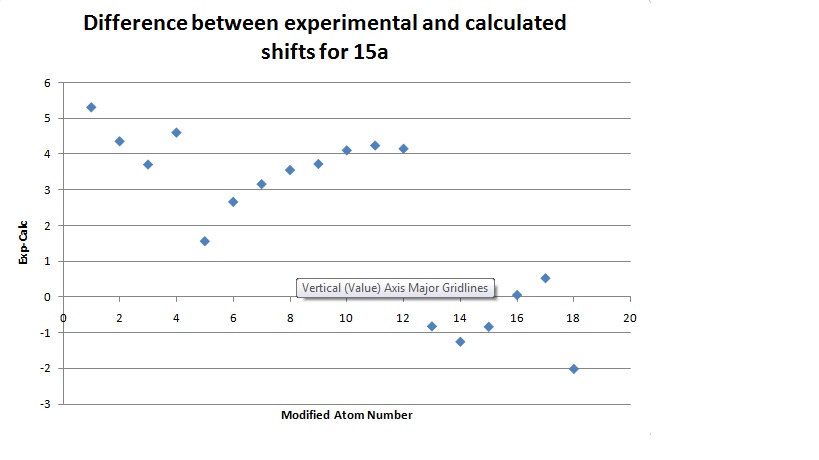
Comparison
The graph shows that the calculation is generally a good one with only one calculated peak being more than 5ppm away from the experimental value. The calculation seemed to work very well at low ppm and less well at high and middle shifts. This may be because of the approximations involved in combining peaks in the same environment. It is clear from the graph that most of the differences are positive, indeed the average of the results is 1.8502. This may be because of problems in modelling a molecule that can rotate it's bonds as much as 15a, but it may also be a problem in the calculation itself. If the latter is the case then it may be possible with more examples to find a fudge factor to correct for this. The average deviation from the experimental results was 2.3950 and was found by finding the average of the mods of the results. This is a relatively small error and shows that this calculation is good for predicting real molecules.
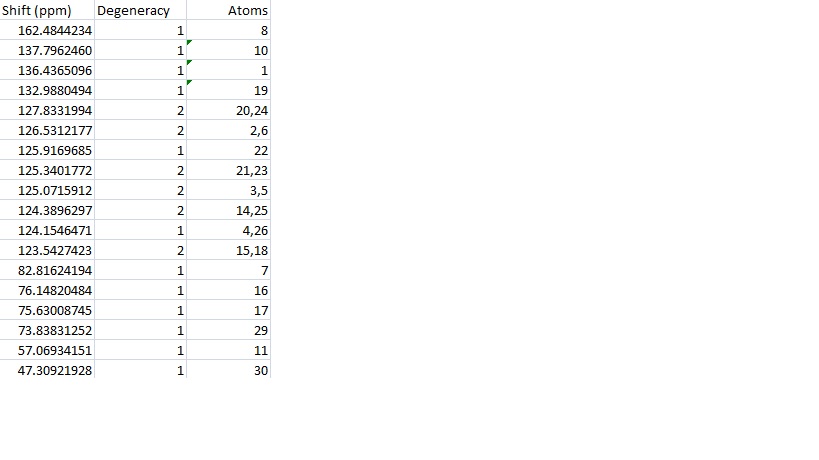
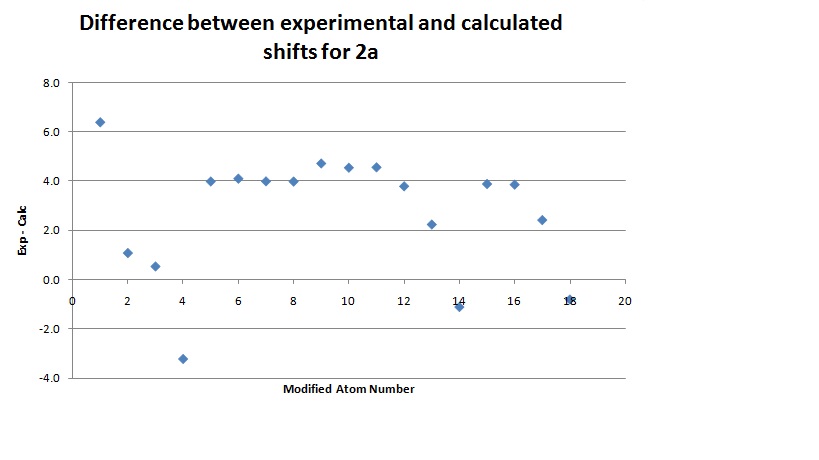
The same technique was then used for 2a.
This data was then combined with the literature values for comparison and a graph of the differences drawn.
The differences between the results are again encouraging. There is only one result above 5ppm which suggests again that the calculation has been successful. There is again many more positive differences than negative (average of the results is 2.7355) which supports the idea of including a fudge factor. In this calculation there doesn't seem to be any difference between the modified peaks and the others which, contrary to 15a, suggests this approximation is a good one.
A proton NMR was considered, however as it would show no differences between the isomers and demonstrates the same understanding as was used for the C13 NMR analysis this has not been included in the project. The J3 couplings would also not provide any additional information so, like the proton NMR, have not been included.
Mechanism
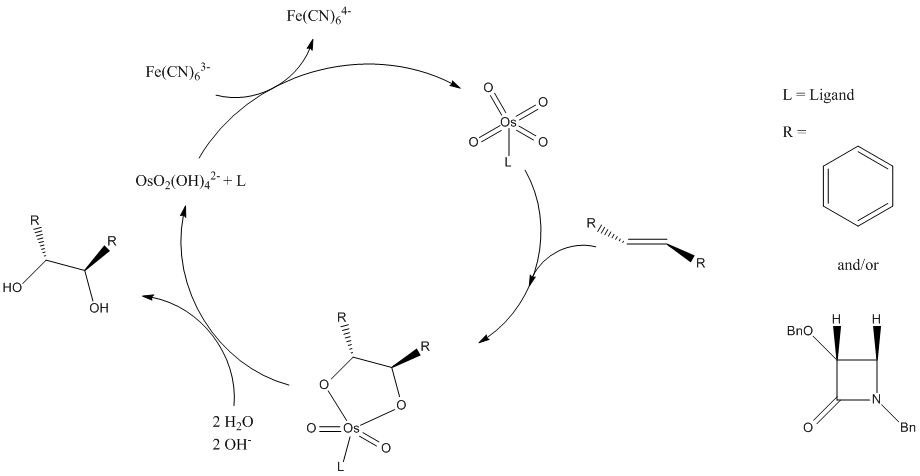
The mechanism from 3a to 15a and 2a is a Sharpless dihydroxylation. The reaction mechanism shown below is from the point of view of the osmium catalyst and the two mechanisms below that explain how two isomers are produced. Since osmium is expensive, it is desirable that it should act like a catalyst rather than as a reagent in reactions, so it can be used again. In this reaction the osmium is reduced in the formation of the product, if left in this reduced state a stoichiometric amount of osmium would be needed. Instead a much cheaper iron oxidising agent (in this case the Fe(CN)63- anion with iron in oxidation state +3) is added to restore the osmium and allow it to act as a catalyst. It then undergoes a [3+2] cycloaddition with the reactant
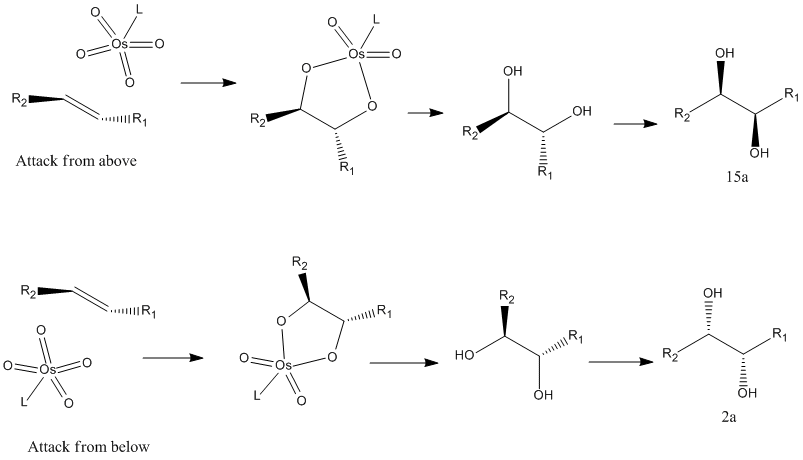
The alkene can be attacked from two directions which results in the formation of the different isomers 15a and 2a. The image below shows how this occurs. In the literature the ratio of the products is determined by the ligand used with the osmium catalyst. If α ((DHQ)2PHAL)) is used the ratio is 15:85 while if β ((DHQD)2PHAL) is used the ratio is 98:2. Clearly this change is hard to model with the methods in this course. Both isomers show similar energies using MM2 and MOPAC minimizations so thermodynamically there would not be much selectivity. The choice of ligand on the catalyst must therefore affect the kinetics of the reaction, giving the product that takes the least amount of energy to form.
References
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838.[1]
- ↑ 2. Pentacyclo[8.2.1.12,5.14,7.18,11]hexadeca-1,7-diene and its 4,5,10,11-tetramethyl derivative, two highly hyperstable next term slightly pyramidalized dienes Pelayo Camps*, Francesc Pérez and Santiago Vázquez [2]
- ↑ 3.0 3.1 B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447
- ↑ IR Absorptions for Representative Functional Groups [3]
- ↑ A β-Lactam-Based Stereoselective Access to β,γ-Dihydroxy α-Amino Acid-Derived Peptides with Either α,β-Like or Unlike Configurations, Claudio Palomo, Mikel Oiarbide, Aitor Landa, Aitor Esnal and Anthony Linden [4]