Structural and Spectroscopic Evaluations using Molecular Mechanics and Semi-empirical Molecular Orbital Methods

The Hydrogenation of the Cyclopentadiene Dimer

Introduction

Dimerisation of cyclopentadiene, the original Diels-Alder diene, proceeds via Huckel topology involving only suprafacial components: a _π4_s + _π2_s cycloaddition:

The endo dimer predominates. Hydrogenation of the product gives two dihydro derivatives (below).

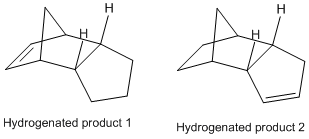
The purpose of this part of the module is to verify/determine the type of control (thermodynamic vs. kinetic) which gives the products of both sets of reaction. The MM2 method with Chem3D is used to optimise the geometry of the cycloaddition products first: comparing the energies of the endo and exo products determines the type of control which gives the endo product predominately. Using the MM2 method to compare the energies of both dihydro derivatives gives a qualitative prediction of the product formed on a thermodynamic basis. The stretching, bending, torsion, van der Waals and H-bonding energy terms are used to compare the relative stability of the dihydro derivatives.

Results and Discussion

Fig. 1.1c Product 1: Endo-dimer, 34.0005 kcal/mol	Fig. 1.1d Product 2: Exo-dimer, 31.8832 kcal/mol	Fig. 1.1e Product 3: Dihydro derivative 1, 35.6948 kcal/mol	Fig. 1.1f Product 4: Dihydro derivative 2, 31.1540 kcal/mol

The MM2 calculation identifies the endo product as the kinetic product and the exo product as the thermodynamic product (34.0005 kcal/mol vs. 31.8832 kcal/mol). The stability of the exo product over the endo product can be rationalised by considering Newmann projections along the two new C-C bonds: the R groups are syn-periplanar in the endo form and anti-periplanar in the exo form. Since the endo product predominates, it is evident that this reaction is under kinetic control.

Table 1.1 - MM2 Geometry Optimisation
Product	1	2	3	4
Parameter	Energy / kcal mol^-1
Stretch	1.2566	1.2896	1.2751	1.0967
Bend	20.8548	20.5855	19.8565	14.5079
Stretch-bend	-0.8350	-0.8393	-0.8333	-0.5504
Torsion	9.5063	7.6715	10.8156	12.4976
Non-1,4 VDW	-1.5368	-1.4355	-1.2195	-1.0513
1,4 VDW	4.3075	4.2335	5.6381	4.5127

Out of the dihydro derivatives, product 4 is thermodynamically more stable than product 3 (hydrogenation at the Diels-Alder double bond preferred over the cyclopentene moiety). On the basis of thermodynamic considerations, product 2 is formed. Looking at the table opposite, the main gain between products 3 and 4 comes about as a result of a 5.3 kcal/mol stabilisation of bend energy for product 4. There is, however, a 1.7 kcal/mol gain in torsion energy, most probably since the cyclopentene moiety is forced to adopt a strained planar geometry rather than the “envelope” conformation of cyclopentane in product 3. This is offset by a relative gain for product 3 in 1,4 VDW interactions: a difference of 1.1 kcal/mol. Differences in stretch, stretch-bend, and non-1,4 VDW energies are marginal and don’t contribute significantly to the overall energy difference.

In summary, the endo product predominates the cycloaddition as the kinetic product, and product 4 predominates the dihydrogenation as the thermodynamic product.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD⁺ analogue)

Introduction

This part of the project investigates the conformations available to 2 pyridinium rings, "A" and "B", with a view to explaining the apparent stereochemistry of the products. The reactions are shown below:

Pyridinium ring “A”, an optically active prolinol derivative, undergoes nucleophilic attack by the Grignard reagent MeMgI at the carbon para- to nitrogen.

Pyridinium ring “B” reacts with aniline to form the addition product.

The conformational analysis using the MM2 force field focuses more on the relative rather than absolute energies of products in various conformations. This allows an explanation of why the methyl/aniline groups are delivered with the stereochemistry displayed. The orientation of the carbonyl group on each pyridinium ring is of particular interest since two potential outcomes are possible: 1) the carbonyl group acts to chelate the incoming nucleophile, the nucleophile adds to the same face as the carbonyl group, or 2) the carbonyl group increases steric repulsion on one face, the nucleophile adds to the opposite face as the carbonyl group.

Results and Discussion

Cycloheptane has 4 major conformations: boat, twist-boat, chair, and twist-chair^[2]. Accordingly, 4 starting conformers are drawn for each pyridinium ring system, one for each major conformation. The energy difference between the two major conformers of cyclopentane is small and so only the envelope conformation is considered in the starting geometries.

Table 1.2a - Pyridinium ring "A" MMFF94 Geometry Optimisations
Starting geometry
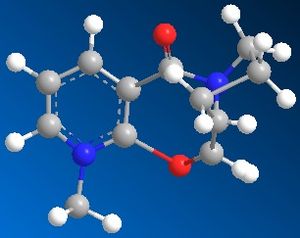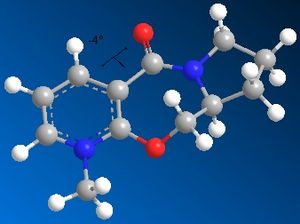
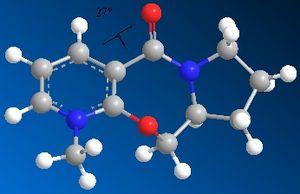
Optimised geometry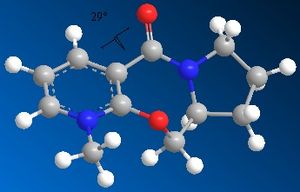
Energy kcal/mol	60.7734	60.9119	57.5094	60.8662
Dihedral angle ^o	29	27	-4	27

The optimised geometries from the boat, chair, and twist-chair conformations give very similar values for energy, and the carbonyl group is raised above the plane of the benzene ring moeity by ~27^o. The conformation resulting from the twist-boat geometry gives the lowest energy, with the carbonyl group below the plane of the ring.

The Me group adds to the same face as the carbonyl group. This occurs via chelation of the nucleophile.

Table 1.2b - Pyridinium ring "B" MMFF94 Geometry Optimisations
Starting geometry
Optimised geometry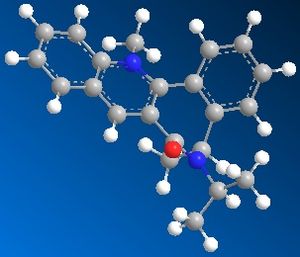
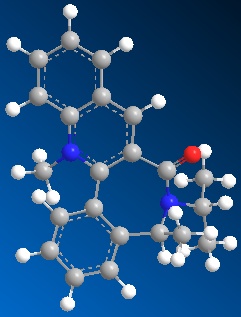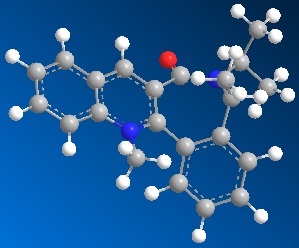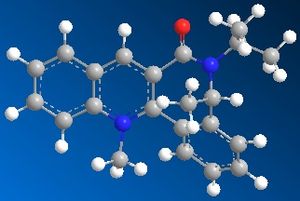Energy kcal/mol	99.6208	112.992	98.4863	98.6754
Dihedral angle ^o	-35	27	-35	-34

The optimised geometries from the boat, twist-boat, and twist-chair conformations give very similar values for energy, and the carbonyl group is below the plane of the naphthalene moeity by ~35^o. The conformation resulting from the chair geometry gives the highest energy, with the carbonyl group above the plane of the naphthalene moeities.

The NHPh group adds to the same face as the carbonyl group. This occurs via steric repulsion between the incoming nucleophile and the carbonyl group.

To improve the study, possible effects of stereochemical control can be investigated by using a quantum mechanical method (e.g.: B3YLP) to calculate the MOs, in particular the LUMO of the pyridinium ring systems as electrophiles and the HOMO of the nucleophiles. This may absolutely determine the stereochemistry of the resulting products. Also, a QST2 or QST3 study may be employed to map out the PES: possible kinetic barriers to reaction may be identified.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Introduction

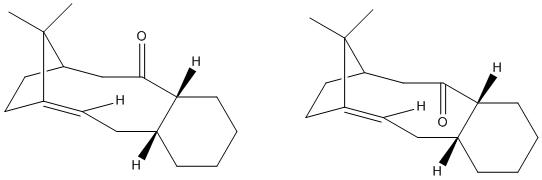
Fig. 1.3a^[1] Atropisomers of taxol total-synthesis intermediates

A key intermediate in the synthesis of Taxol has the carbonyl group orientated either up or down. On standing, the intermediate undergoes atropisomerism: the molecule explores the local PES and isomerises to the lower energy isomer, which is a thermodynamically driven process. The MM2 force field is used to determine the most stable isomer and to rationalise why the subsequent functionalisation of the alkene occurs slowly. The results from the MM2 method are compared with those from the MMFF94 field.

Results and Discussion

With the starting geometries shown below, the two isomers and their energies are found via MM2:

Fig. 1.3b Isomer 1, starting conformation	Fig. 1.3c Isomer 1, MM2 geometry optimisation, 41.2110 kcal/mol	Fig. 1.3d Isomer 2, starting conformation	Fig. 1.3e Isomer 2, MM2 geometry optimisation, 35.5189 kcal/mol

The starting geometries were chosen to be as close as possible to one another, apart from the orientation of the carbonyl group, to allow a fair comparison to be made after MM2 optimisation.

Evidently isomer 2, with the carbonyl group pointing down, is of lower energy than isomer 1, and it thus the isomer observed on standing. The difference is torsional strain is a key factor for this result (see table below), which is rationalised by observing that for isomer 1, the C=O bond is in the same plane as C-H bonds for carbons β, γ, δ, but for isomer 2 the synplanar C-H bonds are located further away at carbons γ, δ, δ.

Table 1.3 - MM2 and MMFF94 Geometry Optimisations
Method	MM2	MM2	MMFF94	MMFF94
Isomer	1	2	1	2
Parameter	Energy / kcal mol^-1
Stretch	2.0129	1.6675	-	-
Bend	11.5787	9.3227	-	-
Stretch-bend	0.2586	0.2360	-	-
Torsion	17.7227	15.5720	-	-
Non-1,4 VDW	-1.8513	-2.4532	-	-
1,4 VDW	11.3007	10.9465	-	-
Total	41.2110	35.5189	51.3835	43.7177

Both isomers 1 and 2 are hyperstable olefins^[3], meaning that they are reluctant to undergo hydrogenation across the double bond against conventional theory. Performing an MM2 calculation starting at the geometrically optimised hydrogenated derivative of isomer 2 shows than the final energy of the product is 40.0509 kcal/mol vs. 35.5189 for the unsaturated product. The proposed hydrogenation is endothermic and must possess a high activation energy to the TS as a kinetic barrier to reaction. The origin of the increase in energy is from an increase in the already constricted ring strain going from sp² to sp³.

MM2 optimises the structure by "jiggling" the bonds in a molecule rather than investigating the effects of moving individual atoms, which can lead to additional strain terms and lead away from the intended minimum. In this case though the optimised structures seem close to the global minimum: there are good indicators that the energy cannot get much lower (e.g.: the cyclohexane moeity in both isomers has adopted a chair conformation).

Using the MMFF94 force field generates higher estimations for energy (~+9 kcal/mol in each case). MMFF94 doesn't account for olefinic strain energy.

Modelling Using Semi-empirical Molecular Orbital Theory

Part 1 Introduction

The reaction of the dialkene structure given with electrophiles such as dichlorocarbene or peracid is dictated by orbital control. In modelling, quantum mechanical methods are required rather than molecular mechanics methods (e.g.: B3LYP rather than MM2) to predict starting geometries, molecular orbitals and energies.

The MM2 force field is applied prior to the quantum mechanical method to get close to the optimised geometry. Then the geometry is optimised under the MOPAC/PM6 method to show molecular orbitals and energies.

Results and Discussion

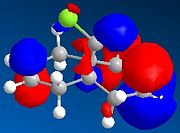
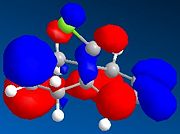
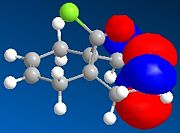
The HOMO-1, HOMO, LUMO, LUMO+1, LUMO+2 molecular orbitals are displayed below:

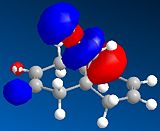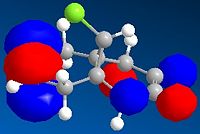Fig. 1.4b HOMO-1	Fig. 1.4c HOMO	Fig. 1.4d LUMO	Fig. 1.4e LUMO+1	Fig. 1.4f LUMO+2

In the reaction, the dialkene acts as the nucleophile. Therefore, it is the HOMO of the dialkene which interacts with the LUMO of the electrophile. Clearly, the double bond with the most electron density in the HOMO diagram is the one on the same side as the Cl atom (the more favred alene is the endo alkene). Not considering kinetic or steric factors (which may prevent the proposed reaction from occuring), the quantum mechanical method shows that it is this bond which participates in the reaction.

Considering the LUMO of the electrophile dichlorocarbene, the symmetry of the proposed frontier orbitals match along the plane of the ring, suggesting a possible mechanism and resulting stereochemical selectivity to attack the face away from the Cl atom (proposed due to steric factors).

Part 2

IR spectra were calculated after specifying the following route section for both files:

# B3LYP/6-31G(d,p) Opt Freq

The two molecules considered were "A" and "B":

Fig. 2.1h	Fig. 2.1i

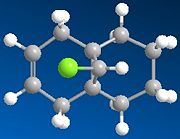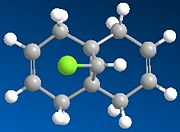The spectra are below:

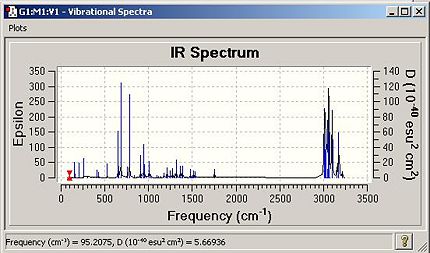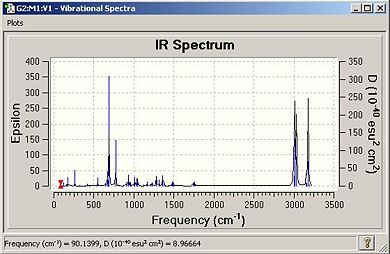Fig. 2j IR single bond	Fig. 2k IR double bond

The table lists the major stretches for each molecule:

Table 1.3 - IR data for "A" and "B"
Stretch	"A"/cm-1	"B"/cm-1
C-Cl	770.91	779.93
C-Cl	930.07	910.37
C-Cl	952.35	940.29
C=C(opposite side from Cl)	1737.12	N/A
C=C(same side as Cl)	1757.37	1753.76

The double bond of “A” is stronger than that in “B”, confirming that the electron density at the double bond in A is greater than that in B as found in part 1 via the MO studies.

Mini project: High-level Geometry Optimisation and Spectroscopic Characterisation of Z,E isomers from the HWE reaction

Introduction

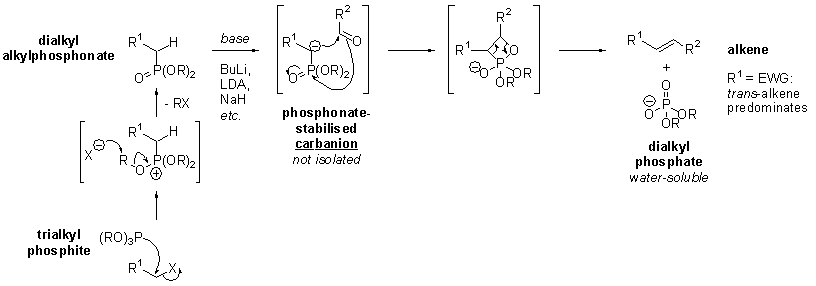
The Horner-Wadsworth-Emmons reaction (HWE reaction) is a significant modification of the Wittig reaction (Nobel Prize, 1979), giving predominantly E-alkenes via stabilised phosphonate carbanions and aldehydes:

Fig. 2.1a^[4]: Mechanism of the HWE reaction

The reaction chosen is the formation of ethyl (4S,2Z)-4,5-(cyclohexylidenoxy)pentenoate via the HWE reaction, recorded by Ando et al ^[5]. Given that the HWE reaction is generally E selective, it is of great interest to synthesise Z-α,β-unsaturated esters via the HWE route.

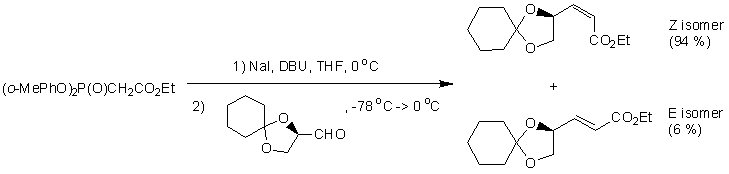
Fig. 2.1b^[2]: Scheme of case study reaction

This reaction is suitable for study since only two diastereoisomers can form (Z and E), the experimental data is well documented (¹H NMR,¹³H NMR, optical rotations, mass spectrum available), the molecule has a low degree of conformational flexibility ignoring the alkyl chain (the cyclohexane moeity only adopts chair and boat conformations, the cyclopentane moeity only adopts an envelope conformation), the molecular formula is C₁₃H₂₀O₄ so a preliminary molecular mechanics refinement is possible for geometry optimisation, and there are only 17 non-hydrogen atoms in the system so the computation is not excessively expensive.

Results and Discussion

Geometry optimisation

Several conformational possibilities were initially sampled in ChemBio3D using the MM2 method:

Fig. 2.1c E conformation 1, 32.2638 kcal/mol	Fig. 2.1d E conformation 2, 42.5715 kcal/mol	Fig. 2.1e Z conformation 1, 34.6108 kcal/mol	Fig. 2.1f Z conformation 2, 52.5795 kcal/mol

All conformers have the cyclohexane moeity in a chair configuration and the cyclopentane moeity in an envelope conformation. The conformers with the lowest energy have the R-C and the O-R' sigma bonds of the RCOOR' ester group app. Not only does this reduce steric hindrance (cf. spp), the app conformation allows a n_Osp2->σ*_C=O anomeric interaction not achieved in the spp conformation. For the Z conformer then, there exists a local minimum on the PES at 52.5795 kcal/mol and the global minimum at 34.6108 kcal/mol. The Z conformer is the thermodynamic product of the pair.

After the initial MM2 geometry optimisation, the route sections for both input files (one for the Z isomer, one for the E isomer) were specified as such:

# MPW1PW91/6-31G(d,p) Opt (maxcycle=25)

After submitting both files to SCAN, the following .chk files were obtained:

Fig. 2f Z isomer	Fig. 2g E isomer

¹³C NMR

The route sections were specified for the optimised geometries of both isomers:

# mpw1pw91/6-31g(d,p) geom=connectivity NMR scrf(cpcm,solvent=chloroform)

The carbon atoms are numbered as above in Fig 2h and i. The journal records the solvent as CDCl₃.

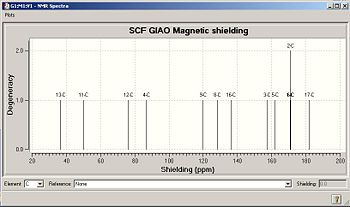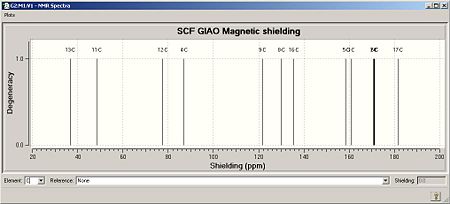Fig. 2f ¹³C NMR Z isomer	Fig. 2g ¹³C NMR E isomer

Table 2a - NMR Data for Z isomer
Carbon No.	Calculated shift/ppm	Literature shift/ppm
13	36.84	14.16
11	50.11	23.81
12	76.37	25.12
4	86.96	34.89
9	119.92	36.20
8	128.28	60.39
16	136.24	69.31
3	157.24	73.14
5	162.05	110.38
6	170.80	120.64
2	170.90	149.54
17	182.03	165.89

The comparison beteen the computed and literature values is very poor: there is little similarity even in differences between peaks. There are limitations in the computational approach, and challenges in obtaining the same conformation between computational studies and experimental results. These will be identified later when considering the results from the IR spectra.

Published locations: Z isomer NMR: http://hdl.handle.net/10042/to-3724 E isomer NMR: http://hdl.handle.net/10042/to-3725

³J_H-H coupling

The Karplus equation is:

J (ϕ) = A \cos^{2} ϕ + B \cos ϕ + C

J is the ³J coupling constant, $ϕ$ is dihedral angle, A, B, and C are empirically-derived parameters^[6].

Considering the vinyl protons, the dihedral angle on the Z isomer is approximately 180^o while the dihedral angle on the E isomer is approximately 0^o. It is therefore expected that the two isomers can be distinguished by considering the ³J_H-H coupling constants of these protons.

Using the Janocchio facility, the following coupling constants are found:

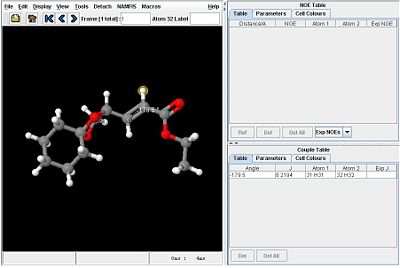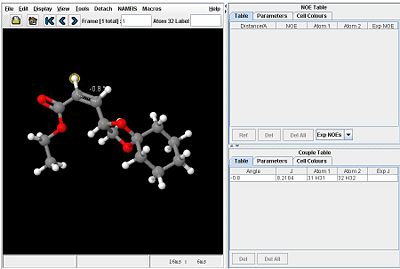Fig. 2h ³J_H-H coupling Z isomer: 8.2194 Hz	Fig. 2i ³J_H-H coupling E isomer: 8.2184 Hz

Since the coupling constant of the Z isomer is slightly higher than that of the E isomer, the value of B in the Karplus equation must be small and negative.

IR spectra

The IR spectra for each isomer was calculated, the route section specified as:

# b3lyp/6-31G(d,p) freq geom=connectivity

Fig. 2j IR Z isomer	Fig. 2k IR E isomer

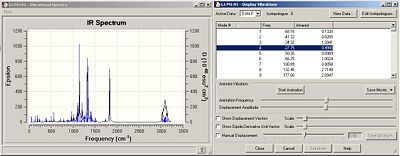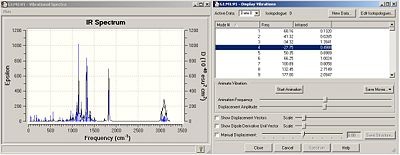There are 4 imaginary frequencies for each isomer. This shows that the optimised geometries are, in fact, transition states. This explains why the ¹³C NMR computed and literature values are so different (the geometries are non-identical).

References

^[1] - Henry Rzepa, "Module 1", last modified 18 Jan 2010, last acessed 29 Jan 2010, http://www.ch.ic.ac.uk/wiki/index.php/Mod:organic

^[2] - Pickett et al, "Conformations of Cycloheptane", JACS (1975), (97), 688, http://pubs.acs.org/doi/pdf/10.1021/ja00837a001

^[3] - W. F. Maier, P. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891-1900. DOI:10.1021/ja00398a003

^[4] - Donald Craig, Lecture 6, "Organic Synthesis" lectures at Imperial College London

^[5] - Ando et al, "Z-Selective Horner-Wadsworth-Emmons Reaction of Ethyl (Diarylphosphono)acetates Using Sodium Iodide and DBU", J. Org. Chem., 2000, (65), 4745-4749

^[6] - Dalton, Louisa (2003-12-22). "Karplus Equation". Chemical & Engineering News 81 (51): 37

Structural and Spectroscopic Evaluations using Molecular Mechanics and Semi-empirical Molecular Orbital Methods

The Hydrogenation of the Cyclopentadiene Dimer

Introduction

Results and Discussion

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ analogue)

Introduction

Results and Discussion

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Introduction

Results and Discussion

Modelling Using Semi-empirical Molecular Orbital Theory

Part 1

Introduction

Results and Discussion

Part 2

Mini project: High-level Geometry Optimisation and Spectroscopic Characterisation of Z,E isomers from the HWE reaction

Introduction

Results and Discussion

Geometry optimisation

13C NMR

3JH-H coupling

IR spectra

References

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD⁺ analogue)

¹³C NMR

³J_H-H coupling