Rep:Mod1:axg2010autumn
Third Year Computational Laboratory 2010 - Organic Module
Modelling using Molecular Mechanics
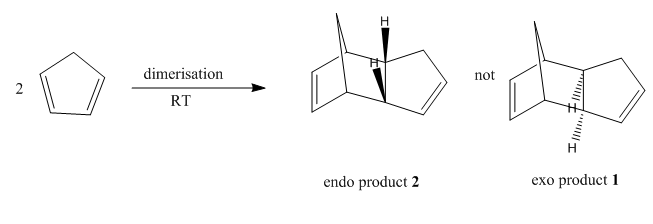
Dimerisation of Cyclopentadiene
It was shown by Wilson et al[1] that cyclopentadiene readily dimerises at room temperature via an Diels Alder cycloaddition, giving only the endo product 2 instead of the exo product 1. The reaction scheme is shown below:
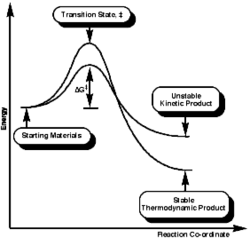
Looking at the reaction scheme of the formation of both products on the left, it is clearly seen that the starting material passes over a smaller energy barrier to give the relatively unstable kinetic product, which is shown to be at higher energy. Nonetheless, this product can climb back this small barrier and then overcome a larger activation energy barrier to furnish the more stable thermodynamic product. This product is not likely to come back over to the starting point due mainly to the activation energy being very large.

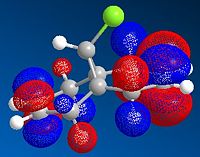
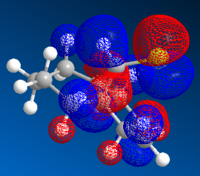
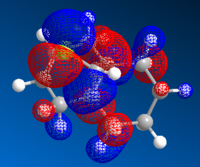
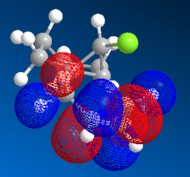
The exo product 1 is the thermodynamic product, which is considered to have lower energy than the kinetic endo product as the exo dimer is less sterically hindered. The endo dimer demonstrates 1,4 strain resulted from the hydrogens on the alkene double bond on the hexene ring and the pentene ring, and therefore less thermodynamically favoured. This result is consistent with the energy generated in Molecular Mechanics 2 calculation (Table 1), in which the endo product 2 has a total energy of 34.0022kcal/mol whereas the exo product 1 is only 31.8834kcal/mol in energy. Most Diels Alder reactions are governed by endo rule[3], i.e.the endo products are preferentially formed, which is the kinetic product with higher energy. Specifically speaking, the secondary p orbital interactions between the HOMO of the diene and LUMO of the dienophile readily stabilise the endo transition state (see picture on the right), and hence enable the reaction to proceed irreversibly.
| Dimerisation Product | Stretching / kcal mol-1 | Bending / kcal mol-1 | Torsion / kcal mol-1 | Van der Waals / kcal mol-1 | Dipole-Dipole / kcal mol-1 | Total Energy / kcal mol-1 |
|---|---|---|---|---|---|---|
| exo product 1 | 1.2923 | 20.5870 | 7.6715 | 4.2320 | 0.3778 | 31.8834 |
| endo product 2 | 1.2466 | 20.8677 | 9.5082 | 4.3321 | 0.4485 | 34.0022 |
Hydrogenation of Cyclopentadiene Dimer
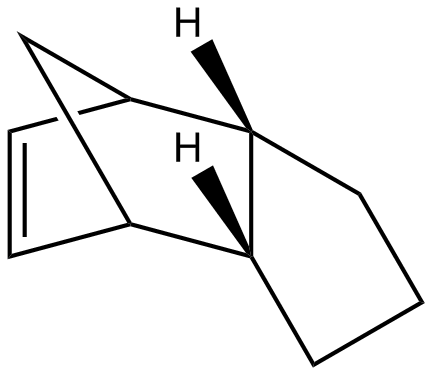
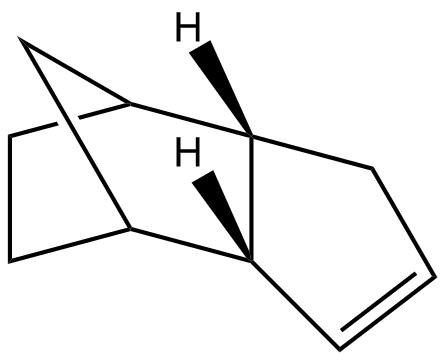
The endo-dicyclopentadiene 2 can be further hydrogenated to give monoalkene and even a tetrahydro product if long reaction period is allowed. The reaction scheme is shown below:

Similarly the hydrogenation process has its thermodynamic and kinetic selectivity. To explore the dominating pathway, the energies of the two monoalkene products 3 and 4 were calculated using Molecular Mechanics 2 method and compared as the following:
| Energy Type | Monoalkene 3 (Endo Dimer) | Monoalkene 4 (Exo Dimer) |
| Energy/kcalmol-1 | Energy/kcalmol-1 | |
| Stretch | 1.2729 | 1.1016 |
| Bend | 19.8541 | 14.5118 |
| Stretch-Bend | -0.5483 | -0.5483 |
| Torsion | 10.8175 | 12.5061 |
| Non-1,4-VdW | -1.2079 | -1.0588 |
| 1,4-VdW | 5.6326 | 4.5042 |
| Dipole/Dipole | 0.1621 | 0.1407 |
| Total Energy | 35.6990 | 31.1574 |
Discussion of Thermodynamic v.s. Kinetic In Hydrogenation
Referring to the reaction profile shown previously, the lower activation energy barrier will yield the less stable kinetic product and the higher activation energy barrier will lead to the thermodynamically stable product. Comparing the total energy illustrated in Table 2, monoalkene 4 has an overall energy of approximately 4.5kcal/mol lower than monoalkene 3. Therefore monoalkene 4 is concluded to be the kinetic endo product and monoalkene 3 is the thermodynamic exo product. Again governed by endo rule, the kinetic product 3 was expected to predominately formed. This is consistent with the experimental observation by Skala et al[4]. The energy difference between two potential products is resulted mainly from the bending energy of ca. 5kcal/mol, which means that product 4 contains fewer deviations from the desired bond angles, i. e. it is subject to more ring strain than product 3, more specifically, product 3 has its double bond in a six-membered ring whereas product 4 bears the latter in a five-membered ring (smaller ring size). The bond angle for an sp2 is ideally 120˚; the bond angle is however 112.2˚ for product 4 and 107.9˚ for product 3, which is even smaller and thus more strained. The other energy contributions are similar in general.
The Molecular Mechanics 2 calculation provides reasonable minimised energy data within short calculation time, which is a useful means of predicting the major product in a range of reactions that may potentially yield mixtures and exploring the more stable transition states.
Stereochemistry of Nucleophilic Addition to A Piridine Ring (NAD+ Analogue)
Chelation of Grignard with N-Methylpyridiniumoxazepenone
Molecule 5 can undergo alkylation with Grignard on 4-position of its pyridinium ring to give a methylated product with its formed methyl anti-periplanar to the hydrogen shown in the scheme below. Usually Grignard reagents readily attack from either face of a flat aromatic system, however this is not the case here:
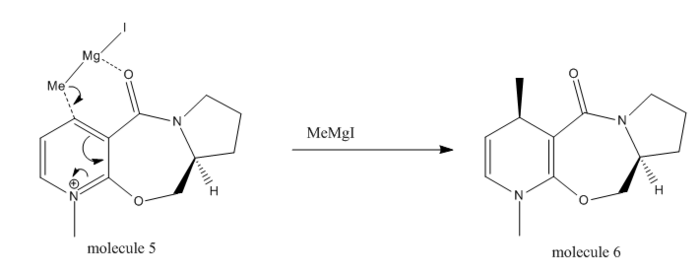
This nucleophilic addition is highly regioselevtive and stereoselective. Shultz et al[5] reported that the electropositive Mg quasi coordinates to the electronegative amide Oxygen atom, as demonstrated in above scheme, subsequently transfer the methyl group from the top face of the 4-position of the pyridinium ring selectively. By changing the conformation of the molecule, three contrasting conformations with very different total energy were generated by moving the amide functionality with respect to the aromatic plane, as shown in Table 3.
Click the following to find Jmol view:
Amongst the three manipulated structures of compound 5, the first conformer has the lowest total energy and therefore is the most stable conformer. The angle between the pyridinium ring and the oxygen atom of the amide group is the smallest for conformer 1, and the dihedral angle increases with increasing total energy. We can safely draw the conclusion that the most favourable conformation is the one with the amide CO sits relatively on top of the aromatic plane at an angle of 11.3 degrees, rather than being perpendicular to the ring system or even larger angles. This hence explains the delivery of the nucleophilic methyl group attacks the pyridinium ring preferentially from the face that provides the accessibility of coordinating to the amide oxygen, i.e. the orientation of the CO determines from which face the alkylating agent attacks. Here the Molecular Mechanics 2 calculation yields a perfect prediction for the regio- and stereo- selectivity for the nucleophilic alkylation with the pyridinium ring systems.
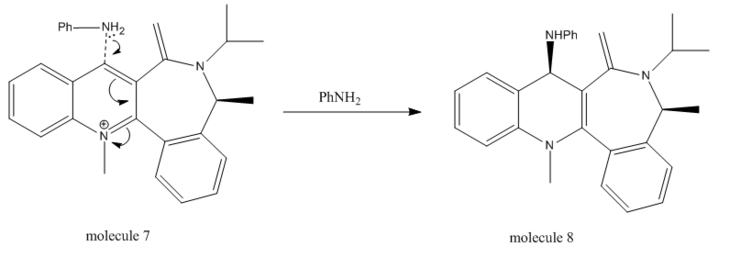
Reaction of Quinolinium Salt with Analine
Similar as above, quinolinium salt can undergo nucleophilic attack from the top of its pyridinium ring selectively. The reaction mechanism is shown below:
The energy of molecule 5 with the most optimised conformation was calculated to be 63.3010kcal/mol; the dihedral angle, i.e. the angle between the oxygen on the amide functionality and the C4 on the pyridinium ring, was -17.9˚. Several experiments were run using MM2 to explore correlation between different energies and dihedral angles by manually changing the configuration of the molecule, followed by minimisation, the results of which are shown in Table 4 with Jmol models.
It is found that the total energy of the molecule decreases with the dihedral angle: conformer 1 was shown to be the most stable with smallest dihedral angle, the CO fraction sits slightly below the aromatic system by a small angle of 17.9˚. This result is invaluable and convincing and can be used to explain the stereoselectivity of this nucleophilic addition: Since the C=O group lies slightly below the aromatic plane, the bottom face was blocked sterically and attacking from top face becomes considerably favourable. Therefore the analine ends up on the same face as the methyl group adjacent to the isopropyl, this methyl, although also pointing upwards, has little steric effect on NHPh addition. Consequently, this result is consistent with the experimental observation by Leleu et al[6] confirming the diastereofacial selectivity to the steric control forced by amide C=O.
| Conformer | comformer 1
|
comformer 2
|
comformer 3
| |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stretch | 4.0782 | 7.3814 | 8.8872 | |||||||||
| Bend | 11.9588 | 89.7610 | 117.7474 | |||||||||
| Stretch-Bend | 0.4155 | 0.7703 | -0.0914 | |||||||||
| Torsion | 9.2794 | 85.5837 | 24.6729 | |||||||||
| Non-1,4 VDW | 4.2788 | 3.2619 | 9.3014 | |||||||||
| 1,4 VDW | 29.3241 | 38.1831 | 39.1466 | |||||||||
| Charge/Dipole | 8.8488 | 10.0249 | -6.1275 | |||||||||
| Dipole/Dipole | -4.8826 | -4.5039 | -3.3918 | |||||||||
| Total Energy | 63.3010 | 170.4625 | 190.1448 | |||||||||
| Dihedral angle /Degrees | -17.9 | 130.7 | -179.0 |
Improvements in Methodology
Molecular Mechanics 2 is surely considered to be a popular and efficient computational method. However this method is not very accurate compared to other method like MOPAC (Molecular Orbital PACkage)[7] and DFT (Density Functional Theory)[8], these two methods also provide information such as electronic/band strucutre of molecules and therefore demonstrate and predict more properties of a wider range of molecules with more accuracy. More importantly, the MOPAC method is able to minimising the energy of two or more configurations and/or conformations at the same time with respect to one another, this gives a great advantage in predicting the most stable product amongst the mixture of products or the one that is more likely to form. Hence it is a very useful means in synthetic chemistry research.
In terms of the reactions/molecules being examined, it was noted that the molecule could adopt many conformations, i.e. the conformation could be changed freely, therefore there were more than one energy minimum (only the one with VERY different energies were reported above). This clearly does not result in a good feasible prediction for the formation of products. In that sense, a bulky group can be introduced to reduce the number of possible conformations/configurations and thus fix the geometry to a greater extent.
Stereochemistry and Reactivity of An Intermediate in The Synthesis of Taxol
Molecule 9 and 10 were reported to be the key intermediates in the synthesis of taxol[9]. Isomer 9 was observed to atropisomerises to isomer 10 upon standing[10], the isomerisation process is illustrated below:
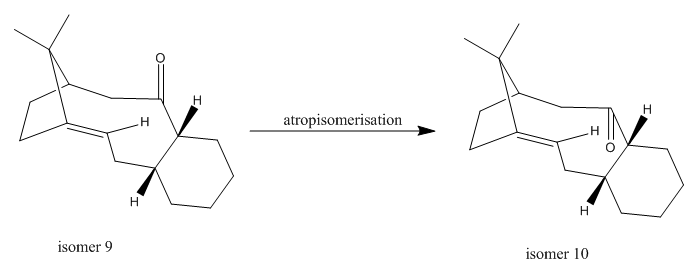

The total energy of both isomers were minimised by MM2 method and MMFF94 method, the results of which were listed in Table 5 and 6. The key to minimisation for either isomer is to ensure the cyclohexyl ring in chair conformation, instead of the less stable boat conformation. MM2 however could not detect from the ChemBio 3D drawing, and is not able to automatically change the cyclohexyl ring to the chair shape. In this case, the conformation has to be changed manually by dragging the carbon atoms around and repeating the minimisation run. It was shown that for both isomer 9 and 10, the boat conformation always has a total energy of ca. 5.5kcal/mol higher than that of the chair conformation.
Comparing the energies of the two conformers, the one with the carbonyl group pointing downwards (isomer 10) has a smaller energy than the 'up' isomer 9, and hence isomer 10 is stabilised by ca. 5kcal/mol energy. The reason why isomer 9 is destabilised slightly is that the transannular strain is present between the hydrogen adjacent to the caybonyl oxygen. This ring strain is considered to be stabilised by the C-H sigma bond interacting with the pi* antibonding orbital of C=O bond. In the meantime, due to the upwards orientation of the carbonyl group, isomer 9 is also experienced steric hinderance exerted by the bulky cyclopentyl and cyclohexyl rings, which were both forced to point down. This result was confirmed by the computational calculations, where the van der waal repulsion for isomer 9 is slightly greater than isomer 10.
The main feature for this alkene is that it is a hyperstable olefin[5], which means that they are quite reluctant to hydrogenation of the C=C double bond, which is very unusual. The alkene is therefore considered to be less strained than the parent alkane. To increase the rate of the reaction, one can play around with the reaction conditions, which may minimise the steric effect exerted by the methyl group on top face, hence pushing the equilibrium of the reaction to another side.[11]
| Conformer | boat isomer (MM2 result) | chair isomer (MM2 result) | chair isomer (MMFF94 result) |
|---|---|---|---|
| Stretch | 2.8159 | 2.6942 | - |
| Bend | 16.4288 | 15.8162 | - |
| Stretch-Bend | 0.4524 | 0.4012 | - |
| Torsion | 21.3594 | 18.1408 | - |
| Non-1,4 VDW | -0.8068 | -0.9261 | - |
| 1,4 VDW | 14.0312 | 12.6212 | - |
| Dipole/Dipole | 0.1376 | 0.1059 | - |
| Total Energy | 54.4185 | 48.8983 | 70.5484 |
| Conformer | boat isomer (MM2 result) | chair isomer (MM2 result) | chair isomer (MMFF94 result) |
|---|---|---|---|
| Stretch | 2.6550 | 2.5274 | - |
| Bend | 11.0780 | 10.6899 | - |
| Stretch-Bend | 0.3479 | 0.3234 | - |
| Torsion | 23.0257 | 19.6036 | - |
| Non-1,4 VDW | -0.9546 | -1.2044 | - |
| 1,4 VDW | 13.9625 | 12.5640 | - |
| Dipole/Dipole | 0.1745 | 0.1816 | - |
| Total Energy | 49.9661 | 44.3223 | 60.5627 |
Click the following to find the most stable conformation (chair) of isomer 9 and 10 Jmol view:
Modelling Using Semi-empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
The addition of dichlorocarbene to the naphthalene shows high regioselectivity under orbital control. Syn-monoadduct was the only product observed by Halton et al[12]. The reaction scheme is shown as follows:
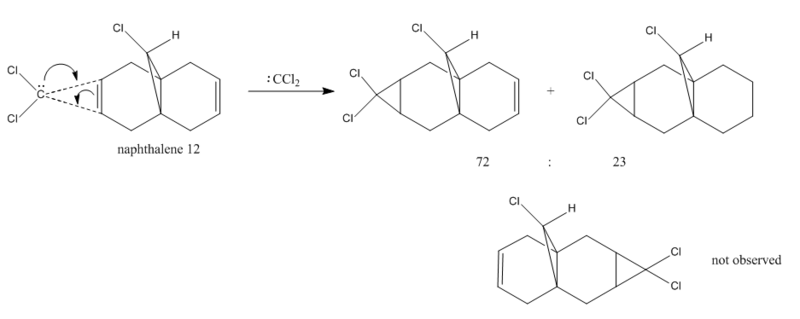
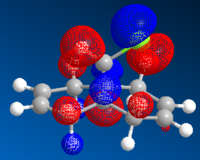
The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) play an important role in determining the reactivity of molecules. Therefore the orbitals close to HOMO and LUMO were produced using ChemBio3D, where the bonding and anti-bonding orbitals were shown in red and blue respectively.
| HOMO-1 | HOMO | LUMO | LUMO+1 | LUMO+2 |
Since nucleophile is the electron-species, therefore results in a filled molecular orbital; whilst electrophile is the electron-deficient species, therefore gives an empty molecular orbital. The interactions between molecules arise from HOMO of the nucleophile and LUMO of the electrophile. LUMO and LUMO+2 orbitals are given by pi* orbitals and LUMO+1 orbital represents C-Cl sigma* orbital. Importantly, the key interactions for this reaction are the ones between the occupied syn-alkene orbital (because the syn-alkene is ore nucleophilic than the anti-alkene) and the unoccupied C-Cl sigma* orbital (i.e. LUMO+1). Orbital mixing is also expected to take place as firstly, this interaction occurs around the HOMO-LUMO region; secondly, LUMO+1 orbital is unoccupied. Orbital mixing results in the bonding orbital being more stabilised and anti bonding orbital more destabilised. It is concluded that the overall energy is stabilised as there are no electrons on the destabilised orbital, i.e. empty orbital has no effect on overall energy.
Mono-hydrogenated Naphthalene 13 and The Influence of the C-Cl bond
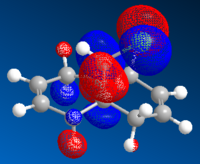
Upon hydrogenating only the anti-alkene of compound 12 gave compound 13. Molecular orbitals close to the HOMO and LUMO region were also generated for the mono-alkene as previously, as shown in Table 8:
| HOMO-1 | HOMO | LUMO | LUMO+1 | LUMO+2 |
By looking at the molecular orbital diagrams of both compounds, it can be seen that both have a large electron density in syn C=C
bond and C-Cl bond region, due to the presence of the electron withdrawing Cl and the electron rich alkene. Therefore the effects exerted by C-Cl bond could not be studied properly only by inspecting the molecular orbitals.
To investigate the influence of the C-Cl bond on the vibration frequencies of the molecule, a DFT based B3LYP/6-31G(d,p) method was introduced to compute the IR frequencies for both compounds. The spectrum and a list of key functionality being studied are shown as follows:
| Molecule | C-Cl stretch/cm-1 | C-Cl stretch/cm-1 (lit.)[13] |
syn C=C stretch/cm-1 | syn C=C stretch/cm-1 (lit.)[14] |
anti C=C stretch/cm-1 | |||
Compound 12
|
770.88 (strong) | 780 (medium~strong) | 1757.37 (weak) | 1620-1680 (weak) | 1737.14 (weak) | |||
|---|---|---|---|---|---|---|---|---|
Compound 13
|
776.90 (strong) | 780 (medium~strong) | 1761.69 (weak) | 1620-1680 (weak) | N/A |
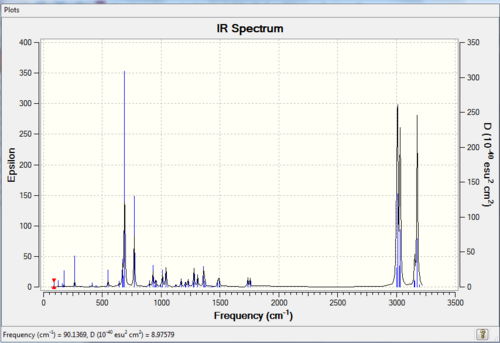
Both spectra look very similar, however there ARE slightly different from each other: From Table 9, both the syn-alkene and C-Cl are higher in wavenumbers for the hydrogenated product, which indicates the energy (see Table 10 below) is higher (energy is proportional to wavenumbers), the molecule is therefore less stabilised. This means that hydrogenation of the anti C=C double bond does not give rise to significant change the stretch of the syn C=C bond; whilst the C-Cl bond is indeed strengthened in the absence of anti C=C double bond. Hence it shows that there is a donation of electron density from the syn-alkene orbital to the C-Cl sigma* orbital, resulting in reasonably strong interactions. If the interaction is even stronger, i.e. more electron density is donated to the C-Cl sigma* orbital, a tetracoordinated carbonium ion (non-classical type) will be formed[15].
| Compound | Total energy / kcal mol-1 |
|---|---|
| 12 | 17.8971 |
| 13 | 22.3472 |
Structure based Mini Project using DFT-based Molecular Orbital Method: E-Selective Horner-Wadsworth-Emmons Reaction of Aldehydes with bis-(2,2,2-trifluoroethyl)phosphonoacetic Acid
Introduction
Horner-Wadsworth-Emmons reaction is a modified Wittig reaction, in which a stabilised phosphonate carbanions reacts with a carbonyl group to give selectively E-alkenes. Compared to the Wittig reaction, where a phosphonium ylid is used as the nucleophile, HWE reaction uses a more basic phosphonate-stabilised carbanions (in this project, a phosphonoacetate), which is a better nucleophile. The work-up also became simpler after modification, as the side product, dialkylphosphonate salt, can be easily removed upon organic/aqueous layer extraction.
The aim for this mini project was to look at a reaction based on computational analysis, more specifically, to predict potential isomeric products that are spectroscopically distinguishable (enantiomers, for example, give the same NMR spectrum, thus it is not studied here). The spectroscopic methods involved in the analysis are IR and C13 NMR, which were done for all predicted isomers with pre-optimised geometry. This result can then be used prior to/along with synthesis of the desired products.
Reaction Scheme and Mechanistic Explanation
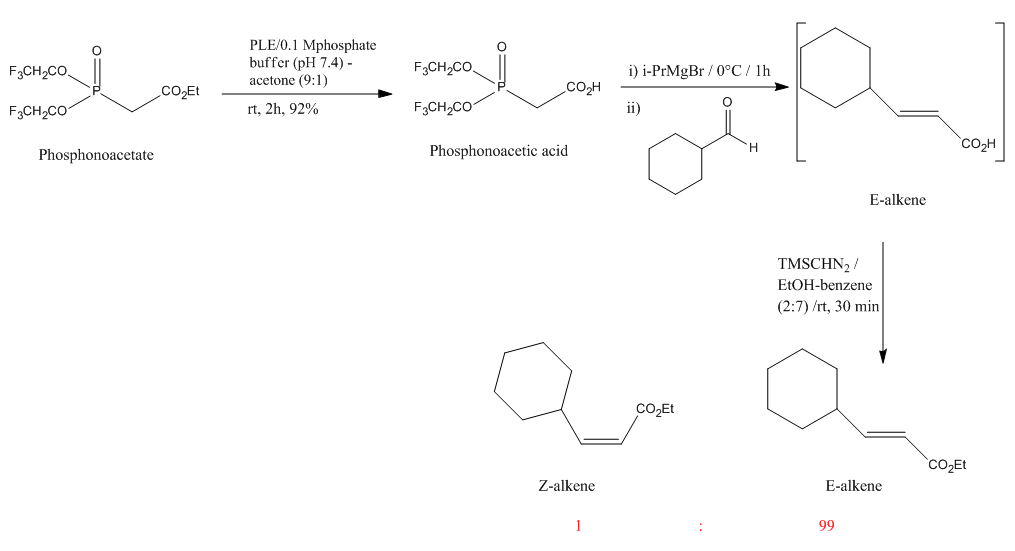
This reaction below was chosen from a series of HWE reactions taken from literature[16]. The reaction scheme is shown as follows:
The mechanism for this HWE reaction is also shown below:
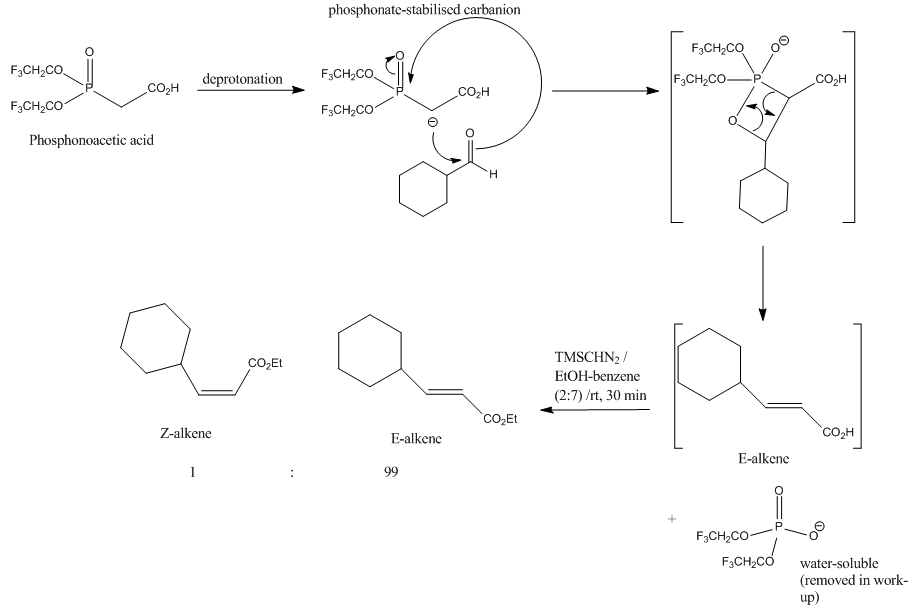
The driving force for this reaction is the formation of the strong P=O bond.
Geometry optimisation
This reaction only produces two diastereoisomers, E- (99%) and Z- (1%) alkene. And both isomers are not too comformational flexible, because the molecules are quite simple, and to pre-minimise the energy before MM2 and MPW1PW91 calculations, the cyclohexyl ring was drawn in chair conformation rather than boat.
Purely by inspecting the molecules and applying chemical knowledge, the trans-alkene is more stable than the cis-alkene. Because the bulky groups on the two ends of the C=C bond prefer to stay as far away from each other as possible, to avoid steric hindrance. The geometry of both molecules were optimised using MM2 with total energy, then were submitted for SCAN using MPW1PW1 method for geometry optimisation. The results are listed below:
| MPW1PW1 result | e-alkene
 |
z-alkene
 |
|---|---|---|
| MPW1PW1 Jmol | ||
| MM2 result | e-alkene
 |
z-alkene
 |
| MM2 jmol | ||
| Total Energy (MM2) | 15.9115kcal/mol | 20.0985kcal/mol |
From Table 11, the total energy of E-alkene is about 5kcal/mol lower than Z-alkene, which means the E-alkene is more stable. This confirms the steric rationalisation above is true.
13C NMR of E- and Z- Alkene
The 13C NMR were calculated via GIAO for both isomers, and the results were compared with literature values, as shown as follows:
| Carbon Number | E-alkene Computed Shift / ppm | E-alkene Literature Shift[16] / ppm | Z-alkene Calculated Shift / ppm | Z-alkene Literature Shift[16] / ppm |
|---|---|---|---|---|
| 1 | 34.4 | 33.9 | 37.2 | 30.5 |
| 4 | 36.0 | 34.3 | 35.5 | 35.0 |
| 2 | 82.1 | 51.4 | 83.8 | 51.1 |
| 13 | 136.0 | 121.4 | 136.0 | 119.9 |
| 3 | 147.4 | 126.2 | 160.0 | 126.0 |
| 5 | 161.2 | 140.7 | 162.0 | 128.4 |
| 9 | 161.2 | 140.7 | 162.0 | 128.5 |
| 7 | 165.2 | 148.4 | 164.5 | 147.1 |
| 6 | 165.7 | 148.4 | 170.0 | 149.4 |
| 8 | 165.7 | 148.4 | 170.0 | 149.4 |
| 12 | 176.4 | 167.0 | 176.3 | 166.7 |
The images with carbon number labels are shown here:
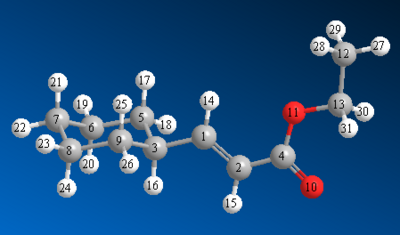
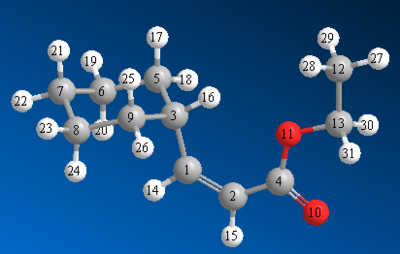

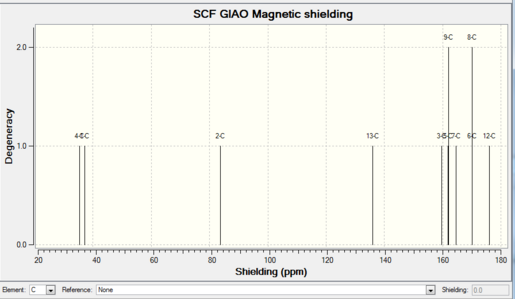
Discussion of the 13C NMR Spectra
E- and Z- alkene should give different chemical shifts on the carbon adjacent to the double bond, and this is the case seen in the calculated values. E-alkene has a chemical shift of 147.4ppm for its C3 carbon, whilst Z-alkene is 160.0ppm on C3. This is the key feature to distinguish between the two diastereoisomers. There are two sets of peaks overlapping in the spectra: C5 signal overlaps with C9 signal, C6 signal overlaps with C8 signal. This is because C5 and C9 are in the same chemical environment, both ortho to C3. Similarly C6 and C8 are both meta to C3, with no other substituents on the cyclohexyl ring. The literature showed similar chemical shifts for the ring carbons as well.
A plot of chemical shift vs carbon number is more descriptive for the comparison with literature.
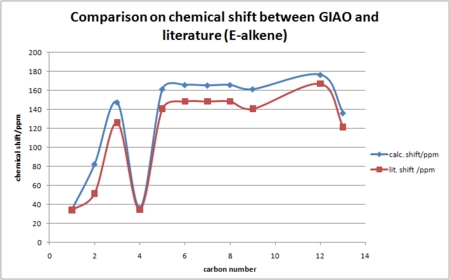
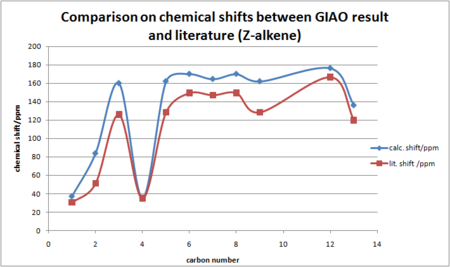
Comparing the GIAO calculated NMR shifts with the literature, it is clear that deviations exist. At lower ppm, the agreement is good. As the ppm increases, the deviation becomes more significant. For C2 on C=C bond, the calculated value is far larger than the literature. For the carbon atoms on the cyclohexyl ring, deviation is similar for all chemical shifts on the ring. For Z-alkene, the chemical shift on C1 is higher than C4, which is not the case in the literature and in E-alkene results. In this sense conclusion cannot be drawn solely based on the computational results, because computational flexibility does exist, the results obtained may not be as reliable as running 13C NMR using spectrometer, which were designed to do certain analysis. Consequently, the GIAO method clearly did not afford a good match with literature.
Infrared Spectra of Diastereoisomers
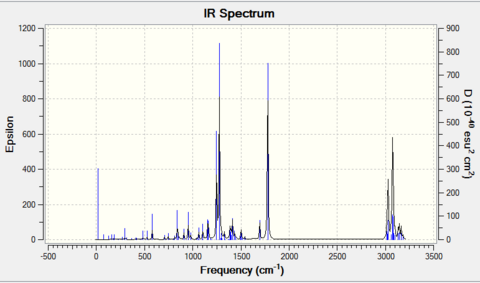
The vibrational frequencies were calculated using B3LYP method, as before. The results were listed in Table 13 and 14, and compared with literature values. The corresponding stretching modes and functionality were also assigned.
| Stretch | Computational cm-1 | Literature cm-1 |
| Scissoring C-C | 1149.57 | 1130 |
| C-H rocking | 1166.11 | 1157 |
| C-H twist | 1286.01 | 1272 |
| C=O | 1707.23 | 1715 |
| =C-H alkene | 3028.67 | 2980 |
| =C-H alkene | 3031.32 | 2980 |
| C-H Stretch | 3072.92 | 3010 |
| C-H Assymetric Stretch | 3082.16 | 3010 |
| Stretch | Computational cm-1 | Literature cm-1 |
| C-C twist | 952.30 | 942 |
| Scissoring C-C | 1155.74 | - |
| C-H twist | 1275.47 | 1270 |
| C=O | 1778.37 | 1716 |
| =C-H alkene | 3027.74 | 2981 |
| =C-H alkene | 3031.26 | 2981 |
| C-H Stretch | 3072.23 | 3011 |
| C-H Assymetric Stretch | 3080.29 | 3011 |
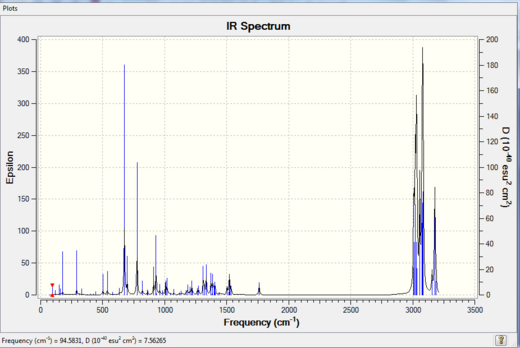
From above two Tables, it can be seen that the scissoring C-C modes are present using computational method and are absent in the literature, i.e. not found using the IR spectrometer. The remaining peaks have similar wavenumbers compared to the literature. Although there is approximately 10 cm-1 difference existing between calculation and experiment, this difference is consistent throughout the spectrum. In this case, a correction factor can simply be introduced to minimise this difference with experimental value, to make the calculation more accurate. Therefore the IR prediction is quite reliable in this particular reaction.
The IR spectra are shown below:

Reference
- ↑ P.J. Jr. Wilson, J.H. Wells, Chem. Rev., 1944, 34, 1. DOI:10.1021/cr60107a001
- ↑ D.A. Widdowson, 'The Chemistry of Nitrogen Compounds', Chap. 4
- ↑ J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry, Oxford University Press, 2001, p.916
- ↑ D.Skala, J.Hanika, Petroleum and Coal, Volume 45, 3-4, 105-108
- ↑ 5.0 5.1 A.G. Shultz, L. Flood, J.P. Springer, J. Org. Chem., 1986, 51, 838: DOI:10.1021/jo00356a016 Cite error: Invalid
<ref>tag; name "axg" defined multiple times with different content - ↑ S. Leleu, C. Papamicaël, F. Marsais, G. Dupas, V. Leavacher, Tetrahedron: Asymmetry, 2004, 15, 3919: DOI:10.1016/j.tetasy.2004.11.004
- ↑ MOPAC2009, J.J.P. Stewart, Stewart Computational Chemistry, Colorado Springs, USA, 2008: website
- ↑ Gaussian 09, Revision A.1, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009: website
- ↑ K.C. Nicolaou, P.G. Nantermet, H. Ueno, R.K. Guy, E.A. Couladouros, E.J. Sorensen, J. Am. Chem. Soc., 1995, 117, 624: DOI:10.1021/ja00107a006
- ↑ S.W. Elmore, L.A. Paquette, Tetrahedron Lett., 1991, 32, 319: DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, 'Rapid Cleavage of Unactivated, Unstrained Amide Bonds at Neutral pH', J. Org. Chem., 2008, 73, 6413–6416 ASAP: DOI:10.1021/jo800706y
- ↑ B. Halton, S.G.G. Russell, J. Org. Chem., 1991, 56, 5553: DOI:10.1021/jo00019a015
- ↑ G. Socrates, Infrared and Raman Characteristic Group Frequencies, 3rd Edition, 2001, p.65
- ↑ J. Coates, Interpretation of Infrared Spectra, A Practical Approach, Encyclopedia of Analytical Chemistry, John Wiley & Sons Ltd, Chichester, 2000
- ↑ E.T. White, J. Tang, T. Oka, 'CH5+: the infrared spectrumobserved', 1999, science 284: 135: DOI:10.1126/science.284.5411.135 ]
- ↑ 16.0 16.1 16.2 S. Sano, U. Takemoto, and Y. Nagao, 'E-Selective Horner-Wadsworth-Emmons Reaction of Aldehydes with bis-(2,2,2-trifluoroethyl)phosphonoacetic Acid', 2003, ARKIVOC 2003 (viii) 93-101