Rep:Mod1:1kr2071

The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

In this module MM2 Allinger calculations were used to not only model molecules, but also to examine more closely properties such as molecular strain, steric effects or stereoselectivity quantitively by defining bond stretches, bond angle distortions, bond torsions, non-bonding VdW repulsions and bond dipoles. MM2 then optimises the model geometry by minimising the total energy by changing these individual bond parameters, i.e. bond lengths, angles and torsion angles.

This computationally relatively simple approach is used in the following exercises to analyse the most stable reaction intermediate or reactivity of a compound. MM2 determines the total energy of a compound as a sum of the above individual non-interacting parameters noted above upon application of a so-called MM2 force field. However, during these exercises the limitations of these simplified calculations will be encountered and further analysed.

The Hydrogenation of Cyclopentadiene Dimer

In this exercise Allinger MM2 molecular mechanics calculations were carried out to examine thermodynamic versus kinetic control of a reaction. This was illustrated using the example of cyclopentadiene dimerisation and subsequent hydrogenation of the dimer.

Formation of the Cyclopentadiene dimer

Cyclopentadiene dimerises via a Diels-Alder cycloaddition. This reaction involves 6 pi-electrons and hence proceeds via Hueckel topology with suprafacial components only with the 2 hydrogens at the ring linkage remaining cis to each other. There are 2 possible outcomes of this reaction, which are shown in Table 1: the endo- and the exo-product.

Table 1: summary of the 2 potential products of Cyclopentadiene Diels-Alder addition

Product	Structure	Total Energy
endo		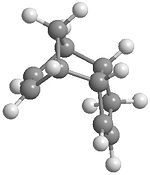34.0029 kcal/mol
exo		31.8849 kcal/mol

As can be seen from the total energies calculated, the exo-product has a lower energy. It is therefore the thermodynamic, i.e. the more stable product of this reaction. Compared to the endo-conformation the eclipsed ring in this exo-compound causes less steric hindrance and the dimer is less strained. Therefore, under reversible conditions, i.e. under thermodynamic control, the exo-product would be formed.

However, it was found that in fact the higher energy, less stable kinetic endo-product of the reaction is formed. This indicates that the reaction must be under kinetic control. In short, rather than the total energy, i.e. stability of the final product, the energy of the transition state controls the reaction outcome. The rate of the reaction, i.e. the activation energy barrier leading to the transition state determines the major product of this reaction. This explains, why the endo-conformation is preferred.

Transition state stabilisation in the endo-conformation

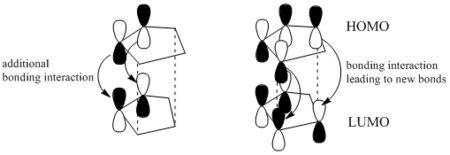
In addition to the primary HOMO-LUMO overlap that essentially leads to the formation of the 2 new sigma-bonds the transition state leading to the endo-conformer is stablised by secondary orbital overlap. This pseudo pi-bond at the back of the diene means additional stabilising bonding interaction, which cannot be found in the transition state giving the exo-product. The endo-transition state is therefore lower in energy and since under kinetic control the endo-conformer is the predominately formed product. This is also referred to as the endo-rule .

Hydrogenation of the Cyclopentadiene dimer

The endo-cyclopentadiene dimer 2 can then be hydrogenated to give either the dihydro derivatives 3, 4 or the tetrahydroderivative 5*, which are summarised in the following Table 2.

Table 2: Summary of relative energies of the hydrogenation products 3, 4 and 5*

	Compound 3	Compound 4	Compound 5*
bend (kcal/mol)	19.8063	14.5224	14.7153
stretch (kcal/mol)	1.2659	1.0944	1.2187
torsion (kcal/mol)	10.8698	12.5071	15.3750
VdW (kcal/mol)	5.6394	4.5046	6.0156
Dipole/Dipole (kcal/mol)	0.1620	0.1402	-
Total Energy (kcal/mol)	35.6953	31.1617	36.1269

In contrast to its formation the hydrogenation of the cyclopentadiene dimer is assumed to proceed under thermodynamic control since we know that compound 5, the tetrahydro derivate is not readily formed. Compound 5 has - compared to compound 4 and 5 - the highest total energy.

In the face of the thermodynamic control of the hydrogenation, it is therefore assumed that compound 4 is the major product, since is has the lowest total energy and hence offers the greatest D(G) driving force for this reaction. Furthermore, the endo-compound (34.0 kcal/mol) must readily hydrogenate to compound 4 (31.2 kcal/mol) since the total energy upon this reaction is reduced and DG=-ve, which would not be the case for hydrogenation to compound 3 (increase in total energy to 35.7 kcal/mol).

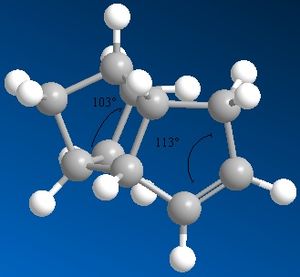
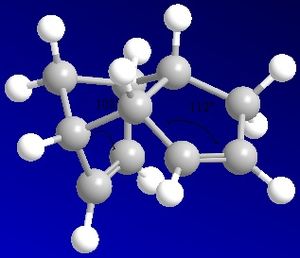
The following images show the bond angle of the alkene to account for the relative energies calculated.

For all 4 compounds bending > torsion > VdW > stretching. The of the energy contributions of bend (3>4), stretch (3~4), torsion (3<4) and VdW (3>4) to the total energy give compound 4 as the major product.

The bond angles measured above further confirm compound 4 as the major hydrogenation product. In compound 4 the more strained double bond next to the bridging-unit in compound 2 is hydrogenated. In the endo-dimer both double bonds experience significant strain since the angle at the sp²-hybridised C is 108^o and 112^o respectively and hence deviates significantly from the ideal 120^o. Therefore, between compound 3 and 4 reaction to compound 4 achieves the greater relief of strain since the doublebond next to the bridging-unit in compound 2 is most contrained (12^o vs 8^o deviation). Compound 3 still contains a highly constrained doublebond. For the hydrogenated single bonds the sp³-C has a bond angle of 103o, which is in agreement with the ideal tetrahedral bondangle of 109^o.

The bend energy term accounts for this increase in energy due to deviations from ideal bond angle conformation and is therefore as expected largest for compound 3 with the 108^o doublebond. The bending energy shows the largest contribution to the total energy. As the total energy of the compound increases, the VdW contributions increase. This is due to the increasing number of hydorgens and hence the increase in steric clash between hydrogens in the 1,4 positon. The stretching of bond lengths stays constant for all hydrogenation products. The torsion, the deviation from dihedral angle at the ring linkage is slightly increased in compound 4 relative to 3 due to the presence of the strained alkene on the RHS of the dimer. Additional torsion is one of the reasons why tetrahydro derivates are unlikely.

The formation and hydrogenation of a cyclopentadiene dimer is also an example for the limitations of MM2 calculations. MM2 only consider the ground state and hence only the thermodynamic stability of a reaction. However, to get a full picture of the chemical reactivity, more information about the energy gap between the starting ground state and the transition state is needed. MM2 calculations are therefore not sufficient to draw conclusions about the kinetic aspect of the reaction. MM2 calculations focus on the position of the individual atoms, however when breaking bonds in a reaction as above more complex calculations have to include the full wavefunction of the structure to be able to model the transition state of a reaction. For MM2 bonding needs to be exactly assigned in the form of single or double bonds.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD⁺analogue)

In this exercise the geometry of the products of the reaction of 2 prolinol derivatives was analysed and subsequently linked to the mechanism of the reaction and the carbonyl-position in the starting derivatives.

Conformation of the starting proline compounds 5 and 7

The conformation of the molecule computed was analysed in terms of its total energy and the dihedral of the carbonyl group relative to the plane of the pyridine ring. Table 3 shows a summary of the total energies found for varying geometry of the starting compounds. Since the pyridine ring and the 5-membered ring are relatively rigid, mainly the position of the carbonyl-oxygen relative to the plane of the molecule and the alignment of the oxygen and the adjacent carbond to the right in the 7-membered ring was changed manually.

Table 3: summary of trial geometries for compound 5 and 7

	Compound 5							Compound 7
dihedral angle / o	7	8	9	10	11	12	22	-20	-22	-124
Torsion / kcal/mol	5.0991	5.0174	5.0319	5.0433	5.1347	5.2081	13.5354	9.6850	9.6941	28.5384
Total Energy / kcal/mol	43.2403	43.1653	43.1229	43.1247	43.1274	43.1488	44.7937	62.6487	63.3840	161.3115

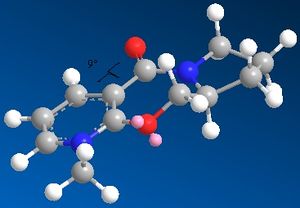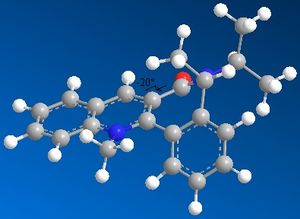Upon trying to change the geometry of compound 5 it was found that due to the inflexible 7-membered ring the carbonyl group can be arranged either in plane or slightly above the plane of the pyridine. Conformations with the carbonyl group below the plane of the molecule were hard to optimise and had energies of 161.41kcal/mol. It was also found that the efficiency of MM2 depends on the inital guess. From Table 3 above, it can be seen that for compound 3 the lowest energy conformation is where the carbonyl is slightly above the plane of the compound by 9^o. In this conformation the balance between steric clash between the carbonyl and adjacent Hs and torsion energy contributions is most favourable. The torsional strain increases, as the carbonyl group moves significantly out of the plane of the molecule due to the deviation in the dihedral angle. To achieve further energy minimisation the position of the oxygen and the carbon to its RHS in the 7-membered ring was manipulated. The most stable configuration with least steric strain was found to be where the oxygen is in the plane of the molecule and the carbon slightly above the plane. Also, the Me-group on the pyridine ring was found to be in the plane of the molecule.

For compound 7 the structure was manipulated in a similar way with the difference that the most stable configuration is with the carbonyl-group below the plane at an angle of -20^o to keep strain of the inflexible ring-components in compound 7 to a minimum.

Both compounds 5 and 7 are an example where the position of the carbonyl group is restricted and cannot be freely rotated due to steric inhibition. Ready rotation would require high steric demand, which cannot be fulfilled by the highly substituted and rigid 7-membered ring in both compounds.

Stereocontrol of the nucleophilic attack on compound 5 and 7

The reaction of compound 5 with a Grignard reagent is highly regioselective to the 4-position as well as stereoselective wrt the orientation of the Me-group added. This is due to the coordination between the Grignard reagent and the amide-O in the course of the reaction. This is also referred to as the Chelation control.

Key steps in this reaction showing the conjugate delivery of Me and the resulting Mg-enolate

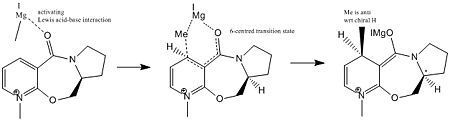
As can be seen from the Transition State this mechanism essentially mirrors an intramolecular addition of Me, which as a result has to be added on the same face as the Carbonyl-group the Grignard is coordinated to, i.e. above the plane of the pyridine ring. In the product the Me-group is anti to the H on the chiral centre.

The selectivity of MeMgI is relatively high, however higher regio-stereoselectivity could be achieved by using bulkier R groups. PhMgBr for instance has a selectivity of >99:1 compared to MeMgBr with 19:1 .

The reaction of compound 7 is also a nucleophilic attack of the 4 position. In this case the nucleophile is added on the opposite face of the Carbonyl to reduce electronic repulsion between the electronegative carbonyl-O and the sterically large elecron-rich Ph-group of the incoming nucleophile.

Nucleophilic attack of 7 by PhNH₂

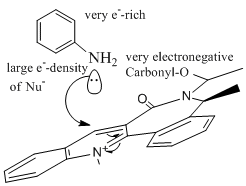
Since as established above the carbonyl group in compound 7 is orientated below the plane of the molecule, in the opposite face of the Me-group on the RHS, in the product NHPh is syn to this Me-group. Applying MM2 calculations on the anti-conformer product, the molecule automatically reverts back with the NHPh group coming out of the plane. As indicated in the image to the left nucleophilic reactions are determined and controlled by high e^--density of the attacking nucleophile, which leads to electronic repulsion and in this case explains the stereocontrol of the product 8.

Note that for all calculations the lowest global energy minima conformation was tried to isolate via a trial-and-error process. However, it is impossible to ensure that the lowest energy conformation was found, especially as the compounds get larger and more complex such as compound 5 or 7 (and in the next section 9 and 10 in particular). For larger ring systems, the trial-and-error approach becomes increasingly insufficient due to infinite number of different conformations. Also, they cannot be parameterised accurately against standard diatomic models, which is what is essentially done when running MM2 models.

As molecules become more complex, the simplifications made in the MM2 calculations no longer hold. For instance for aromotic rings, or highly substituted structures as above, individual bonds cannot be isolated and individual energies cannot be simply added up. To obtain an accurate quantitive estimate of the model the quantum-mechanical aspect in form of the Schroedinger wave fucntion of the molecule has to be taken into account. Furthermore, as established in the example of the Cyclopentadiene dimer, using MM2 one can only make limited assumptions about the reactivity of a modelled structure. To getter a better idea about the electronic aspect of a reaction MOPAC/PM6 could be used (as later in part 1.4).

Another way to solve this problem could be the Monte Carlo method to examine conformations of e.g. bicyclic ring systems as e.g. Taxol intermediates in the following exercise.

It was also tried to optimise the Mg-enolte. This failed as Mg cannot be recognised by the MM2 programme. All parameters contributing to the total steric energy sum upon which MM2 calculations are based on require precise definition of atom types. In order to simplify the calculation, the structure input is essentially approximated by representative diatomic models. All parameters are based on these pre-set models, which does not include transition metals such as Mg.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Structure of the Intermediate

Due to the sterically inhibited and hence restricted rotation of the highly substituted and hence rigid ring structure the intermediate in the synthesis of Taxol isomerises between 2 main structures 9 and 10, shown below. The isolation of 2 isomers due to an energy barrier of rotation is referred to as atropisomerism.

Isomer 9	Isomer 10

Table 4: Energies of isomers 9 and 10

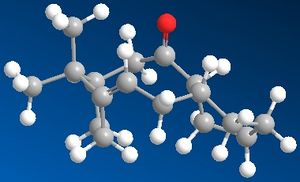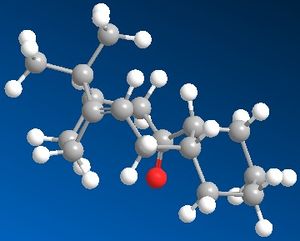	compound 9	compound 10
Bend / kcal/mol	16.5552	10.7550
Stretch / kcal/mol	2.7704	2.5682
Torsion / kcal/mol	20.5854	19.6040
1,4-VdW / kcal/mol	13.9136	12.5222
Total Energy / kcal/mol	54.1027	44.2878

Based on the total energy calculations and individual energy contributions for compound 9 and 10 the most stable isomer is assumed to be compound 10, with the carbonyl group pointing down.

It was also found that in order to achieve an energy minima for compound 9 the cyclohexane-ring has to be in a twisted boat conformation. In contrast to this compound 10 was found to be most stable with the cyclohexane-component in a stable chair conformation. This twist in compound 9 also contributes towards its higher VdW energy (14.1 kcal/mol) compared to compound 10 (12.5 kcal/mol) as in the twisted conformation the ring-hydrogens come within the VdW radius of each other causing repulsive interaction and raising the energy in form if increased transannular strain across the ring. Furthermore, upon trying to optimise compound 9 with the cyclohexane in chair-conformation, the structure always reverts back to a twist-boat, which indicates that in structure 9 the twist-boat conformation is more stable than the chair-conformation due to relief of torsional strain. It was then tried to minimise the a boat conformation. This repulsion of the cyclohexane-ring hydrogens across the ring (transannular strain), however, is assumed to be too large in the boat-conformer

It was also tried to change the orientation of the ring at the alkene and the Carbonyl-attachment, however the most stable configuration is as shown in the images above with the bridgehead alkene and the other, opposite bridgehead C-C pointing away from each other to increase the distance between the 2 hydrogens and avoid destabilising transannular strain.

Since the structural difference between the 2 isomers is small, the energy difference between compound 9 and 10 was not expected to be very large. The 1,4-VdW interaction is large for both compounds as it is primarily due to steric clash between hyrogens adjacent to each other or across the ring (transannular strain). The higher VdW in compound 9 have been explained above. The stretching distortion from ideal bond length is similar as both structures are based on a complex, highly substituted, rigid ring structure. Torsional strain is high in both compounds due to large twisting about single bonds. It is higher for compound 9 as there is higher repulsion between the pointing-up carbonyl and the adjacent hydrogens at the cyclohexane-ring-linkage.

The main difference between 9 and 10 is the bending energy caused by large angle strain. This summarises the stability of compound 10 where the cyclohexane-ring is in a stable chair and the carbonyl is pointing down and therefore less distorted by adjacent H on the ring-linkage, which are pointing up.

Reactivity of the Intermediate-Olefin

The alkene in bridgehead position in this intermediate is unusually stable und subsequently very unreactive, contrary to what would be expected based on Bredt's rule for small rings (focuses on the twisting distortion of pi-bonds in bridgehead alkenes). Normally, the ring and angle strain make the bridgehead position unfavourable for alkenes. However, Bredt's rule can be violated in large enough ring molecules. Isomer 10 is such an example for a hyperstable alkene in bridgeposition. This hyperstability is quantitively defined by the -ve olefin strain OS relative to the parent hydrocarbon As can be seen from Table 4 the main contributions towards the total energy in comopund 10 is the bending component, VdW interactions and Torsion. These contributions are expected to increase even further upon changing the hybridisation from the sp²-hybridised C in compound 10 to sp³ due to functionalisation of the alkene. Due to the larger angle for sp²-hybridised C (120^o vs 109^o) and the more planar geometry relief the large angular strain in isomer 10 relative to a parenthydrocarbon. Also, space is less congested due to a reduced number of hydrogens present for an sp² alkene and destabising transannular interactions reduced.

Modelling using semi-empirical molecular orbital theory

In the following exercise the reactivity of Dichlorocarbene was studied. However, it was established from the previous exercises that one of the limitations of the MM2 calculations is its purely mechanical, i.e. classical approach. Therefore, in the following exercise the MM2 method was extended by using MOPAC/PM6. This means the extension of a purely classical model to a molecular modelling calculation that includes quantum-mechanical aspects, i.e. the wave description of the electrons. The information obtained was then used to explain the reactivity of Dichlorocarbene more accurately.

Reactivity of Dichlorocarbene

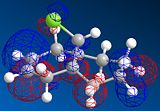
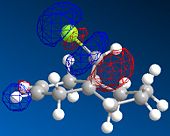
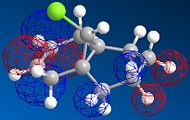
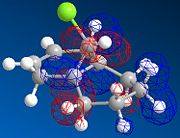
MOPAC/PM6 geometry optimization parameters were used to examine the reactivity and regioselective addition of Dichlorocarbene. MOPAC extends the MM2 optimization and produces approximate molecular wavefunctions of the valence electrons. Table 6 shows a summary of these Molecular Orbitals.

Table 5: Molecular Orbitals of Dichlorocarbene 12 and 12*

	HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2
Compound 12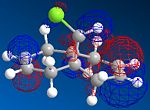
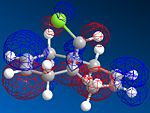
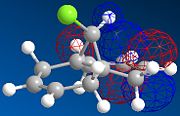
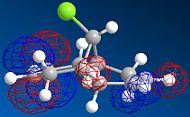
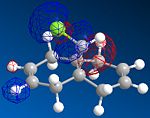
Compound 12*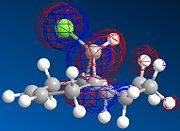

The total energy for compound 12 is 17.9022 kcal/mol calculated using MM2. Upon removal of the anti-doublebond the total energy increases to 24.7857 kcal/mol. The HOMO was defined as being most reactive towards electrophilic attack using MOPAC/PM6.

The alkene on the RHS (as seen in image) in compound 12 is anti wrt to the bridge-Cl-bond, whereas the alkene on the LHS is syn to the Cl-C bond. Based on MM2 modelling there would be no distinction between the 2 alkenes in terms of their reactivity. In the MM2 optimised structure of compound 12 the 2 rings are both in the chair formation and completely symmetrical. However, using MOPAC the wavefuction of the electrons can be defined and hence conclusions about the reactivity and transition states of compound 12 can be made.

It can be seen that e^--density in the HOMO is largest through space for this syn-alkene. Furthermore, the syn Cl-atom is very electronegative, which increases the e^--density in space around the syn-alkene even further. Similar to the the carbonium effect, in this HOMO at the syn-alkene the e^--density is spread out in space between over the bridging Cl to the alkene. The HOMO is therefore assumed to control electrophilic reactivity and stereoselectivity wrt to the syn-alkene.

The more nodes, the higher the energy of the molecular orbital. The order of energy of the molecular orbitals is therefore presumed to be: HOMO-1<HOMO<LUMO<LUMO+1<LUMO+2.

The HOMO and LUMO therefore are defined as the FMOs that determine the reaction reactvity. The HOMO is lower in energy, as there is more e^--density and more constructive overlap on the top and the bottom of the molecule. Hence, there are fewer nodes. The LUMO has more nodes. It is also dominated by the pi* bond on the anti-alkene. Mainly destructive overlaps can be seen. There is many nodes, and low e^--density across the molecule. It is therefore overall anti-bonding.

Vibrational Frequencies of C-Cl and C=C bonds in compound 12 and 12*

The following 2 Tables show a summary of the IR-vibrations for the C-Cl and the C=C bonds in comopund 12 and 12* calculated using MOPAC and Gaussview.

Table 6: IR-data obtained for compound 12

Type of vibration	frequency / cm-1	Relative intensity	Visualisation
C=C stretch (syn)	1757.36	3.9347
C=C stretch (anti)	1737.10	4.2037
C-Cl stretches	770.90	25.1193
	930.07	7.2813

Note, that the C-Cl stretches above were selected based on relative intensity. Other smaller, and hence lower intensity C-Cl stretches were also observed at 548.82 cm^-1, 901.53 cm^-1 and 952.34 cm^-1. However, upon comparing to literature, the main C-Cl stretch for both 12 and 12* takes place in the region of 770 cm^-1. The literature value for C-Cl stretches is 750 cm^-1.

The C-Cl stretching frequencies are at a higher wavelength, i.e. a higher energy is required to achieve a C-Cl stretch, indicating stronger C-Cl bonds. This could be due to overlap of the C-Cl molecular orbitals with the syn-alkene.

Similarly, the both the C=C stretches are at a significantly higher frequency than literature values of 1675 cm^-1.

From the IR-data obtained it can be also seen that the syn-alkene has stronger bonds (higher wavenumber, lower frequency, higher energy). This increased strength of the pi-bond means higher e^--density in that area and the syn-alkene is therefore more susceptible to electrophilic attack.

Table 7: IR-data obtained for compound 12*

Type of vibration	frequency / cm-1	Relative intensity	Visualisation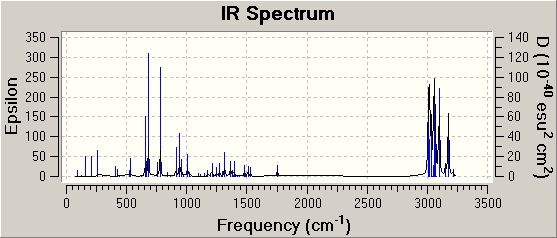
C=C stretch	1753.76	5.0423
C-Cl stretches	779.93	21.3901
	910.37	6.7189
	940.30	10.3191

Compared to the monoene 12*, the C-Cl bond in the diene is weaker (lower wavenumber, less energy required to cause stretching of the C-Cl bond, weaker bonds). This can be related to the molecular orbitals discussed in the previous part. As can be seen from molecular orbital visualisation in the HOMO there is significant overlap between the syn-alkene and the C-Cl bond. The syn-alkene donates e^--density into the C-Cl molecular orbital. However, as can been seen from the image, in the HOMO the C-Cl molecular orbital is in fact of anti-bonding overlap, i.e. essentially e^--density is donated into an anti-bonding orbital, which makes the C-Cl bond weaker in compound 12 than in compound 12*. Also, since there is 2 alkenes in the HOMO of compound 12 there is significant in-phase overlap between the molecular orbitals of the 2 alkenes, i.e. this the delocalisation of e^--density of the alkene orbitals is compensated for by overlap with e^--density from the other anti-alkene. Therefore, there is no significant difference between the syn-alkene stretching frequency in 12 and the alkene stretch in compound 12* despite this partial removal of e^--density. In compound 12* the C-Cl stretch is at higher frequency as there is no donation of e^--density into the anti-bonding C-Cl bond causing delocalisation.

Structure based Mini project using DFT-based Molecular orbital methods

Structure of compound chosen and its formation

The compound chosen is Goniothalamin oxide GO1 and its isomer Isogoniothalamin oxide IGO2. These comopunds and its biological activity are discussed in more detail in the following reference . Each isomer is obtained as an enatiomeric mixture. GO1 and IGO2 were prepared via the epoxidation of (R)- or (S)-Goniothalamin using mCPBA as oxidising agent. The 2 isomers were then isolated using Thin-Layer chromatography carried out on Macherey-Nagel precoated silica plates. Separate sets of ¹³C-NMR, ¹H-NMR and IR data for each isomer are tabulated in the literature.

Mechanism of formation of GO1 and IGO2 using mCPBA

Key mechanistic step for formation of GO1 and IGO2

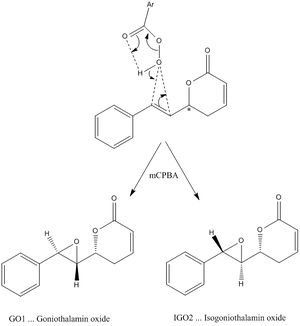
As can be seen this epoxidation using mCPBA proceeds via a concerted mechanism, i.e. the 2 new bonds form simultaneously. As a consequence the initial stereochemistry is maintained. This reaction is stereospecific wrt to the alkene geometry, i.e. it proceeds with retention of configuration of the olefin in the starting material. The epoxide in GO1 and IGO2 remains in trans-configuration.

The pi-system of the alkene acts as the nucleophile that attacks the electronpoor, and thus electrophilic O of the peracid.

However, even though the reaction is stereospecific wrt to the alkene geometry, there is 2 possible arrangements of the epoxide wrt the adjacent 6-membered ring.

MM2 and MOPAC optimised structures of GO1 and IGO2

Table 8: Energies and conformation of GO1 and IGO2

	Goniothalamin Oxide GO1		Isogoniothalamin Oxide IGO2
Stretch / kcal/mol	9.8900		9.8154
Bend / kcal/mol	77.3536		76.6609
Torsion / kcal/mol	1.0340		0.8815
1,4-VdW / kcal/mol	13.7800		13.9947
Dipole/Dipole / kcal/mol	6.0713		5.8242
Total Energy / kcal/mol	104.9927		103.8982

As expected the 2 isomers are very similar in energy. According to the literature the 2 isomers are obtained in a 64%yield, in a 3:2 molar ratio. Therefore, if under thermodynamic conditions it would be expected that GO1 was of lower total energy than IGO2. In fact, it was found that IGO2 is slightly lower in energy compared to GO1. Furthermore, this reaction is unlikely to be under reversible, i.e. thermodynamic conditions. The concerted formation of GO1 and IGO2 is thought to be determined by the transition state and to be irreversible and therefore under kinetic control (refer to Part 1.1). The formation of GO1 is assumed to proceed via the lower energy transition state and hence dominate the ratio of the product mixture. The calculation method MM2 used in this module is therefore not sufficient to make any further conclusions regarding the reactivity of the bond forming and breaking process. Furthermore, this reaction is concerted and has no intermediate and proceeds via one transition-state. However, based on Hammond's postulate this transition state should be similar to the final reaction outcome and hence stabilised by the same factors. Based on that the transition state of IGO2 should be also lower, which would mean that IGO2 is also the kinetic poduct. Since from literature GO1 is determined as the major outcome, DG of the reaction (DG=DH-TDS) is significantly affected by the entropy factor and cannot simply be derived from the heat of product formation (DH and Hammond's postulate).

Both compounds are very strained, i.e. the bending, stretching and torsional energy components are very large. The distortion from ideal angle (in form of the bending energy) forms the largest contribution, indicating the high steric strain of GO1 and IGO2 due to the complex 2-ring structure and an additional epoxide-group on the 3-C link. In order to minimise energy it was found that the 2 rings are twisted to each other. Due to that twist in the structure, hydrogens are likely to come within the Van-der-Waals radius of each other, which would explain the large VdW energy contribution due to these 1,4-interactions.

The total energy of IGO2 is assumed to be lower due to the fact that the epoxide is bent further away from the large 6-membered ester-ring and therefore sterically less hindered.

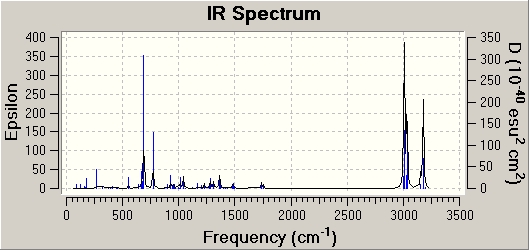
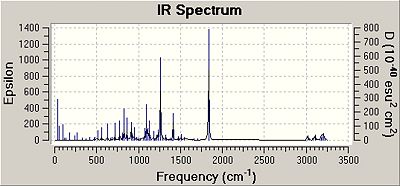
Prediction of the IR-spectra of the GO1 and IGO2 and comparison to literature data

The following table shows a summary of the calculated data obtained and the reference literature data.

Table 9: Calculated IR-frequencies vs literature data for GO1

Literature frequency /cm-1	Predicted frequency /cm-1	Type of vibration	Predicted IR-spectrum for GO1
3420	-	due to H-bonding
3062	3193	aromatic C-H stretch, alkene C-H
2960	3107.1	Csp3-H bend, epoxide C-H bend
1724	1836.19	ester C=O stretch
1631	1642	aromatic C=C stretches
1466	1506.62	aromatic H-rocking
1398	1474	aromatic H-bend
1377	1413.22	alkene C-H rocking
1259	1260.47	ester C-O stretch
1043	1094.87	Csp3-H bend
812	912.04	epoxide C-O stretch
704	828.26	alkene C-H bend in-and out-of-plane, carbonyl O bend

Table 10: Calculated IR-frequencies vs literature data for IGO2

Literature frequency /cm-1	Predicted frequency /cm-1	Type of vibration	Predicted IR-spectrum for IGO2
3072	3205.22	aromatic C-H stretch
2962	3036	Csp3-H bend, epoxide C-H stretch
1726	1836.06	ester C=O stretch
1383	1406.07	alkene C-H bend
1254	1261.61	ester C-O stretch
1074	1089	C-C stretch, ester C-O stretch
1032	898.884	epoxide C-O stretch
879	826.195	alkene C-H bend in-and out-of-plane, carbonyl O bend
818	777	aromatic C-H bend

The computational IR data was obtained as described in the Module1-instructions.

Specific IR-peaks were selected as follows:

First, the literature IR-peaks were roughly assigned to vibrational motions of the GO1 and IGO2. The computational peaks were selected based on intensity (especially when several data points in the same regions were computed). Furthermore, the individual vibrational motion seen in Gaussview was tried to match to what was expected based on literature. After IR-peaks of the first isomer were assigned, similar vibrational modes could be identified in the other isomer.

The key vibrational frequencies for the epoxide C-O stretch, the ester C-O stretch and the ester C=O stretch in both isomers were compared. And subsequently, the efficiency of the computational approach was then determined based on these most distinct vibrations since they could be readily matched to literature IR-stretches (these vibrations are underlined).

Depending on the isomer, the strength of the ester C=O, the ester and epoxide C-O bond changes. This change is accounted for by using the computational approach. It can be seen that the main IR-frequencies could be assigned accurately and were close to literature data.

However, for stretching frequencies an error of +8% has to be taken into account. Also, as the frequency increases, the error between literature and predicted values increases. Lower frequencies calculations as for instance for the epoxide stretch are usually more accurate, however the initial assignment of the epoxide C-O stretch is more difficult and less precise as it takes place in the fingerprint region of an IR-spectrum. IR-spectroscopy itself is therefore not a very effienct tool to distinguish between these 2 isomers. The ester C-O and C=O stretch stay constant. There is a significant difference between the epoxide C-O stretch for the 2 isomers from the calculated data: 912cm-1 in the GO1 versus 898.884 in IGO2. However, it is difficult to assign these peaks accurately in the experimental literature data based on reference epoxide-stretches since - as mentioned - this stretch takes place in the fingerprint region.

A significant difference is that for GO1 some vibrations could not be predicted. This is due to the fact that only predicted calculations fo significant intensity were tabulated. Furthermore, some vbrational frequencies overlap and are accounted for in other more intense peaks.

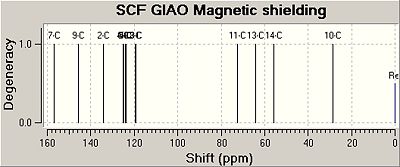
Prediction of the ¹³C-NMR-spectra of the GO1 and IGO2 and comparison to literature data

The results obtained are tabulated in the following table.

Labelling of C-atoms

Table 11: Calculated chemical shifts in the ¹³C-NMR vs literature data of GO1

Literature δ /ppm	Predicted δ /ppm	C-assignment	Predicted 13C-NMR-spectra of GO1
162.8	156.99	C7
144.3	145.55	C9
135.6	134.23	C2
128.7	125.19	C6
128.6 (2C)	124.68	C4
	124.18	C1
125.7 (2C)	123.87	C5
	119.54	C3
121.5	119.1	C8
77.2	72.57	C11
61.5	64.31	C12
57.2	55.67	C13
25.9	28.59	C10

Table 12: Calculated chemical shifts in the ¹³C-NMR vs literature data of IGO2

Literature δ /ppm	Predicted δ /ppm	C-assignment	Predicted 13C-NMR-spectra of GO1
162.8	156.91	C7
144.3	144.98	C9
135.6	133.42	C2
128.6 (3C)	125.24	C4
	124.76	C6
	124.37	C5
125.6 (2C)	123.81	C1
	119.48	C3
121.5	119.65	C8
75.1	77.99	C11
62.1	63.09	C12
55	59.57	C13
26.1	29.26	C10

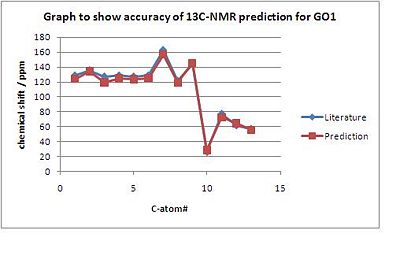
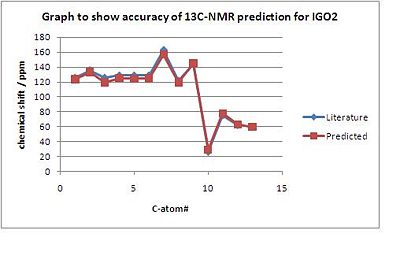
The difference between the literature data and the calculated prediction is shown in the following plots of chemical shift δ / ppm versus the Carbon-#.

The ¹³C-NMR-spectra for both GO1 and IGO2 were found to be in agreement with the literature data. However, there is a max error of 7ppm due to the fact that GO1 and IGO2 have sensitive conformation and when the inital structures for GO1 and IGO2 were optimised using MM2, many conformations with only minimal total energy differences were found. For both isomers the peaks between 128 - 119 ppm were slighlty shifted in the calculated spectrum. This could be due to the fact that in this region peaks very close to each other, and therefore could not have been assigned with a 100% precision in the experimental literature data.

Furthermore, based on literature and computed data there is no significant difference outside the experimental error in the ¹³C chemical shifts, by which the 2 isomers could be told apart.

Prediction of the 3J H-H coupling based on the ¹H-NMR-spectra of the GO1 and IGO2

Based on the literature results the main difference between the 2 isomers is the ³J-coupling constant between the H next to the epoxide on C12 and the adjacent H on C11 of the ester-ring.

Table 13: Literature ³J_HHCoupling constant of 2 isomers

	GO1	IGO2
Chemical shift / ppm	3.27	3.25
Literature data	dd, 1H, J 5.4Hz and 1.9Hz	dd, 1H, J3.4Hz and 1.9Hz

Molecular modelling was then used to define the dihedral angle between these 2 hydrogens. Based on these GO1 and IGO2 were represented in the Newman Projection to define the ³J_HH coupling constant using "Generalized 3JHH calculations acc Haas et al." as linked on the Module 1 instructions.

GO1 - dihedral angle 62o

GO1 - 3JHH 3.47 Hz

IGO2 - dihedral angle 175o

IGO2 - 3JHH 8.47 Hz

Compared to the literature the data obtained in fact shows the opposite trend, i.e. larger coupling in the IGO2 isomer. However, it has to be noted that the method to determine the coupling constant involves several approximations: the alignment in the 3D model is slightly eclipsed which is not accounted for in the Newman Projection. Furthermore, the large side groups are approximated by only 1 atom.

Conclusion

Based on the data above MM2 and MOPAC could be used to predict IR-spectra and 13C-NMR relatively accurately. Apart from 3JHH coupling constants, another useful indicator to differentiate between the 2 isomers GO1 and IGO would be optical rotation. However, the job was sent 3 times to Scan and was failed after running for 22 hours.

An improvement to analyse the 2 isomers would be 2D-NMR, in particular 2D NOESY ((NuclearOverhauserEnhancementSpectroscopy) or 2D COSY, which could be used to examine more accurately the through space relationship between the epoxide-H on C12 and the adjacent H on C11 of the ester-ring, their through-space-separation and subsequently determine the coupling more accurately.

References

Background reading:

1. Kinetic vs Thermodynamic control: Prof. Alan Spivey, Y3-"An Introduction to Stereoelectronics", Lecture2, Autumn 2009
2. Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928 DOI:10.1016/j.tetasy.2004.11.004
3. Evaluation and Prediction of the stability of bridgehead olefins: W.Maier, Paul V.R. Schleyer, J.Am.Chem.Soc., 1981, 103(8), 1891-1900 DOI:10.1021/ja00398a003
4. Formation of epoxides: Prof Alan Amstrong, Y2-"Organic Synthesis", Lecture6, Autumn 2008
5. S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
6. Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928 DOI:10.1016/j.tetasy.2004.11.004
7. D. A. Evans, M. J. Bodkin, S. R. Baker, G. J. Sharman, J. Magn. Reson,, 2007 DOI:10.1002/mrc.2016