Rep:Mod.3jlm07

Module 3

The Cope Rearrangement

The Cope Rearrangement is the very famous thermal isomerisation of 1,5-hexdiene via a [3,3] sigmatropic rearrangement. The main product of the reaction is the thermodynamically more stable regioisomer.

It is possible to use Gaussview to locate low-energy minima and transition structures on the potential energy surface to determine the prefered reaction mechanism.

The anti conformation of 1,5 hexadiene was drawn so that the four central carbon had a dihedral angle of 180⁰. A HF/3-21G optimisation, setting the %memory level to 500MB, was run and the resulting checkpoint file opened. The optimised energy was -231.6854 a.u (to 4.dp). The molecule was symmetrized to give a C2h point group. The resulting molecule is shown below:

Changing the conformation from 180⁰ to 0⁰, i would expect the energy to raise slightly since antiperiplanar tends to be more stable than periplanar in most cases due to better orbital overlap and reduced steric effects. Optimising using the same method, the total energy did increase as expected, from -231.6854 a.u to -231.6724 a.u, and exhibited reduced symmetry changing point group from C2h to C2v as the molecule has lost its sigma-h plane of symmetry. The optimised syn conformation is shown below.

This syn conformation is higher in energy than the app conformation; since these angles comply to both extremes of dihedral angle spectrum, i.e. the groups are either maximum or minimum distance apart, i would expect this syn and anti conformations to maintain as the highest and lowest energy conformations respectively when investigating the inbetween gauche conformations. Since there is an infinite number of gauche conformations possible, i predict the most stable will be that with the double bonds pointing away from each other and at a maximum possible distance; they are the most electon rich areas of the molecule so will repel each other. Manually adjusting the dihedral angle in gaussview, the same calculation was run on gauche conformations. The energy, dihedral angle between the 4 central carbons, and point group was determined from each calculation. This can be seen in the table below and compared to the table values given in the script.

"**Total energy, Point group and dihedral angle of HF/3-21G calculations on 1,5 hexadiene**"
Conformation	Image	Dihedral angle/degrees	Point group	Energy/a.u	Energy/Kcal/mol	Relative energy/Kcal/mol	Table value	Relative table energy/Kcal/mol
gauche 1		75.77	C2	-231.68772	-145389	3.10	-231.68772	3.10
guache 2		-64.16	C2	-231.69167	-145391	0.62	-231.69167	0.62
gauche 3		67.68	C1	-231.69266	-145392	0.00	-231.69266	0.00
gauche 4		60	C2	-231.69153	-145391	0.71	-231.69153	0.71
gauche 5		71.08	C1	-231.68962	-145390	1.91	-231.68962	1.91
guache 6		70.23	C1	-231.68916	-145390	2.20	-231.68916	2.20
anti 1		-176.89	C2	-231.69260	-145392	0.04	-231.6926	0.04
anti2		-179.99	Ci	-231.69254	-145392	0.08	-231.69254	0.08
anti 3		-179.99	C2h	-231.68907	-145390	2.25	-231.68907	2.25
anti 4		178.35	C1	-231.69097	-145391	1.06	-231.69097	1.06

You can see that the lowest energy conformation is gauche 3 with a dihedral angle of 67.7degrees. The energies of the remaining molecules have been made relative to this by taking the difference between the two energy values. There doesnt seem to be a corellation between the dihedral angle and the energy since some angles lower than the 64 degrees in gauche 3, yet still have a lower energy. Therefore, the lowering in energy is likely to be linked to other geometric factors such as bond lengths, other bond angles, and distance the C=C are apart (these factors will be considered later with the anti2 conformation). Gauche 1 has the highest energy conformation with a relative energy of 3.10 Kcal/mol. This conformation also doesnt show a correllation with the dihedral angle. It doesnt have the largest dihedral angle again suggesting there are other geometric factors involved.

All the energies and relative energies agree perfectly with those given in the table in the script impling all the same conformers were possible to reproduce. However, it did take some time to get to these conformations since there is an infinite number possible as you rotate the carbon atoms about 360 degrees.

Overall, the lowest energy conformation is not the anti 180degree conformation but a gauche conformation. The second most stable is the anti 1 conformation. Although, there is a reduced dihedral angle in gauch 3, there must be better orbital overlap and reduced steric hinderence in this molecule to increase stability.

The output files for these are:

Running more accurate Optimisations on anti 2 conformation

The anti 2 conformation has Ci symmetry meaning it is not linear, has no Cn axes of rotations, has no planes of symmetry, but does have a centre of inversion. Running the same optimisation calculation but at a higher level of accuracy, DFT/B3LYP/6-31G(d), the point group remains unchanged. However, the geometries are affected:

"**Comparing HF/3-21G and DFT/B3LYP/6-31G(d) calculations outcomes on anti 2. 1,5 hexadiene conformer**"
'	Method	'
Anti 2 Conformer	HF/3-21G	DFT/6-32Gd
Energy/a.u	-231.6925	-234.6117
Energy/Kcal/mol	-145392	-147224
Point group	Ci	Ci
Bond angles/degrees
C1-C2-C3-C4	-114.64	-118.59
C1-C2-C5-C6	114.64	118.59
C1-C3-C4	124.81	125.29
C2-C5-C6	124.81	125.29
C1-C2-C3	111.35	112.67
C1-C2-C5	111.35	112.67
Bond lengths/A
C3=C4	1.32	1.33
C1-C3	1.51	1.5
C1-C2	1.55	1.55
C2-C5	1.52	1.5
C5=C6	1.32	1.33

You can see how increasing the level of accuracy has changed the geometrys quite considerably; the dihedral angles along the backbone have gained an extra 4degrees spacing, the 3-atom angles have increased by 1degree, and the angle between the carbon backbone and the double bond has increased by about 0.5degrees at each end. The bond lengths however, have stayed approximately the same. All in all, this has resulted in a lowering of the total energy by 1832 Kcal/mol, that is ~3 a.u. This is a fairly large difference in energy and shows how much more accurate using a higher basis set is.

To confirm that all the vibrational frequencies are real and positive and hence that we have reached a global minimum, a frequency calculation will now be carried out on the 6-31Gd optimised molecule. This calculation also allows the optimised energies to be compared with experimentally measured quantites linked with thermochemistry.

So running a frequency calculation on the optimised molecule, gives the following IR spectrum.

The total energy in the frequency calculation matched that of the optimised one, confirming the molecule has not been altered during the calculation. Furthermore, since there are no negative/imaginary vibrations, this confirms the molecule is at a global minimum and hence is safe to use in comparison with the thermochemistry data given in the frequency output file.

"**Thermochemistry outcomes of Freq. calculation on anti 2. 1,5 hexadiene conformer under DFT/6-31Gd basis set**"
'	Sum of electronic and...	'	'	'
unit	Zero point energies	Thermal energies	Thermal enthalpies	Thermal free energies
	E=Eelec +ZPE (T=0K)	E=E+Evib+Erot+Etrans (T=298K, 1atm)	H=E +RT	G=H-TS
a.u (Hartrees)	-234.4692	-234.4619	-234.4609	-234.5008
Kcal/mol	-147134	-147130	-147129	-147154

Optimising the "chair" and "boat" transition structures

Chair Transition State

An allyl fragment was drawn in gaussview and optimised at the HT/3-21G level to generate:

This was then copied and opened in a new window via the edit, paste, append molecule process. This was repeated to give two fragments in the same window and hence to generate a transition like intermediate. The fragments were alligned in the chair conformation like shown below, the terminal carbons being 2.28Å apart between the two fragments.

The optimisation is now ready to be run but cannot be run as simply as for a single molecule since we are not looking at a minimum, we are looking at transition state, therefore, we need to know where the negative direction of the reaction coordinate is. Since we have a reasonable structure for our transition state, we can compute the force constant matrix (Hessian) in the first step of the optimisation which then updates as the calculation proceeds (Method 1). However, in some cases a different approach is needed, particularly when the suggested structure is too far from the real one. In this case, a better structure needs to be generated first and then the optimisation started again from this new structure. This is achieved by freezing the reaction coordinate, minimising the rest of the molecule, unfreezing the reaction coordinate, and the optimisation restarted (Method 2). This second approach can be advantageous and save a lot of time when the force constant calculation is extensive.

Method 1: Force constant calculation method; Running an 'Opt+Freq' calculation under HF/3-21G

This time, instead of running a minimisation, the molecule is optimised to 'TS(Berny)'. The force constants are changed from 'never' to 'once' and the addtional keywords 'Opt=NoEigen' are entered. This calculation generated the image is shown below and one imaginary vibration at -818cm-1, the displacement vectors also shown below.

You can see that these vibrations are consistant with the Cope Rearrangement [3,3] sigmatropic nature by the movement of the carbon pairs that make up the new bonds. At one end, they symmetrically converge towards each other whilst at the other end they symmetrically diverge.

Method 2: Frozen coordinate method; Running minimum Optimisation followed by TS Optimisation

The original guess transtion structure if the two allyl fragments at 2.28Å apart is opened and under the edit menu the Redundent coordinate editor opened. The terminal carbons that form the new bonds under reaction are selected and fixed into a frozen position. Now, a normal Optimisation to find a minimum is run (at HF/3-21G level) with the addtional Opt=ModRedundant reference appearing in the title. The checkpoint file for this is opened, the coordinates unfrozen and the 'deriviative' option selected instead. Now a force constant calculation is run like in Method 1, but instead of selecting 'Once' for the force constant calculation, it is set to 'never'. So, to clarify, an Opt+Freq, TS (Berny), Force constants (Never), calculation was run and the resulting checkpoint file for this opened. The resulting images are:

You can see how the aromaticity has changed with the bond lengths, and how the distance between the bonds being made is optimised. A comparison of the two methods is shown in the table below:

"**Comparing Force constant Method 1 with Frozen coordinate Method 2 for the Chair Transition State**"
'	Method 1	'	Method 2	'	'
	Before	After	Before	Part 1	Part 2
Bond length/A
c4-c12	2.28	2.02	2.20	2.20	2.02
c3-c11	2.25	2.02	2.20	2.20	2.02
C9-C12	1.39	1.39	1.39	1.38	1.39
C9-C11	1.39	1.39	1.39	1.39	1.39
C3-C1	1.39	1.39	1.39	1.39	1.39
C4-C1	1.39	1.39	1.39	1.38	1.39
Bond angle/degrees
C11-C9-C12	124.3	120.5	124.3	121.89	120.5
C4-C1-C3	124.3	120.5	124.3	121.89	120.5
Energy/a.u	-	-231.6193	-	-231.6158	-231.6193

In Method 1, the bond lengths between the two fragments where the reaction actually takes place, lower from 2.28Å to 2.02Å in one calculation. The same result is seen in Method 2 but over two calculations. Firstly, the distance stays the same as those particular bonds are held constant and then they reduce to the same result as Method 1 in the second step. You can also see how these two steps affect the energy too; the TS lying higher in energy in Method 2 part 1, but then reducing to the same energy as Method 1 in part 2. Furthermore, the nature of the calculation in Method 2 Part 1 also shines through as there is a slight change in the allyl fragment bond lengths. This reflects the fixation of the C4-C12 and C3-C11 lengths, allowing the rest of the molecule to relax and optimise and hence change other bond lengths in the molecule. Since Method 1 doesnt have these bonds fixed, this is not observed. The final observation is the reduction in the bond angles about the allyl fragments. They reduce by about 3degrees under the optimisation.

Boat Optimisation

The other transition state possible is the boat conformer. A different method will be used to optimise the geometry to find this transition state; QST2. This is where the reactants and products are put in two different windows of the same file and the calulation runs to try to find the TS between these two windows. This method is sensitive to how the reactants and products are drawn; they need to be individually optimised first and all the atoms labelled correctly to coincide with the reaction thats occuring. So, for this case, the reactant and product are both the anti2 conformation of 1,5 hexadiene and hence the labelling is very important. The labelling of my input is shown below, reactants on the left and products on the right.

The following optimisation was run: # opt=(calcfc,qst2) freq hf/3-21g geom=connectivity and the resulting TS was:

You can see that the TS is not optimum; the calculation has linearly interpolated between the two structures and not considered rotation about the central bonds but merely translated one allyl fragment on top of the other, hence the crossing over of the bonds observed. So how do we locate the TS; modify the molecular geometries of the reactants and products to so that they more closely resemble the TS. The central dihedral angle was changed from 180degrees to 0degrees and the C2-C3-C4 and C3-C4-C5 bonds were reduced to 100degrees from 111degrees. Again the atoms are labelled appropriately.

Again the same calculation was run in gaussview: # opt=(calcfc,qst2) freq hf/3-21g geom=connectivity but this time the resulting TS was:

This shows how the boat TS has now been found and has an optimised energy of -231.6028 a.u. Compare this with the optimised chair energy -231.6193 a.u. since all calulations were run at the same basis set. This confirms that the chair TS is 0.0165 a.u. (10.3540Kcal/mol) deeper in energy and hence would be the favoured pathway as the activation energy to allow the chair TS would be lower. Though in reality, it is difficult to predict which pathway the reaction would take since they are many different conformations (see IRC section).

Yet another method to find a TS can be used, QST3, this involves inputting three images; reactants, products, and a guess TS. This will be used later in the diels alder section.

Following minimum energy path on the potential energy surface; IRC

IRC is the intrinsic reaction coordinate method that allows you to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This was achieved by running a # irc=(forward,maxpoints=50,calcfc) rhf/3-21g geom=connectivity calculation. Output file can be found at: DOI:10042/to-3526 The resulting geometries are:

When a molecule has reached its global minimum the RMS gradient should reach zero. Unfortunately it hasnt here (total energy = -231.6205a.u.) so more must be done to achieve this. there are three ways about going about this, each with their own advantages and disadvantages. 1. Take the last point on the IRC and run a normal Minimisation: # opt rhf/3-21g geom=connectivity.Output file can be found at: DOI:10042/to-3527

2. Restart the IRC and specific a larger number of points until it reaches a minimum: # irc=(forward,maxpoints=100,calcfc) rhf/3-21g geom=connectivity. Output file can be found at: DOI:10042/to-3528

3. Redo the IRC specifying you want to calculate the force constants at every step: # irc=(forward,maxpoints=50,recalc=1,calcfc) rhf/3-21g geom=connectivity. Output file can be found at: DOI:10042/to-3529

You can see from these results, they dont all lead to the same result under these condition. (1) although the fastest calculation, has not reached the minimum, (2) is getting close but has not used enough points (you need to be careful when using more points not to veer off into another minimum) and (3) is the most reliable, but also the most expensive and is not great for larger systems. (3) is the only one to have converged to the optimum minimum where RMS=0. You can see that (2) is similar in conformation to gauche 4 whereas (3) is similar in conformation to gauche 2.

Optimising the Chair and Boat TS to a higher level of accuracy

Taking the HF/3-21G level of accuracy files and optimising them to the B3LYP/6-31G* level, there are some changes observed in the energy levels and the geometries of the two levels, see the tables below:

The chair 6-31G* optimsation can be viewed here: DOI:10042/to-3530 and the boat here: DOI:10042/to-3531

"**Energy comparisons between chair and boat TS optimisations at the HF/3-21G and B3LYP/6-31G* level**"
'	'	Sum of electronic and...	'	'	'
	Total Electronic Energy	Zero point energies	Thermal energies	Thermal enthalpies	Thermal free energies
	(all values in a.u.)	E=Eelec +ZPE (T=0K)	E=E+Evib+Erot+Etrans (T=298K, 1atm)	H=E +RT	G=H-TS
Chair TS HF/3-21G	-231.6192	-231.4667	-231.4613	-231.4604	-231.4952
Chair TS B3LYP/6-31G*	-234.5675	-234.4259	-234.4200	-234.4190	-234.4549
Boat TS HF/3-21G	-231.6028	-231.4509	-231.4453	-231.4444	-231.4798
Boat TS B3LYP/6-31G*	-234.5431	-234.4023	-234.3960	-234.3951	-234.4318
anti2 HF/3-21G	-231.6925	-231.5395	-231.5326	-231.5316	-231.5709
anti2 B3LYP/6-31G*	-234.6117	-234.4692	-234.4619	-234.4609	-234.5008

"**Geometry comparisons between chair and boat TS optimisations at the HF/3-21G and B3LYP/6-31G* level**"
'	Bond length/A	'	Bond angle/degrees	'
	C4-C12	C3-C11	C11-C9-C12	C4-C1-C3
Chair TS 3-21G	2.02	2.02	120.5	120.5
Chair TS 6-31G*	1.98	1.98	120.2	120.2
	C3-C4	C1-C6	C1-c2-C3	C4-C5-C6
Boat TS 3-21G	2.14	2.14	121.7	121.7
Boat TS 6-31G*	2.2	2.2	122.2	122.3

This shows how the energies of both transition states lie alot deeper in energy under the more accurate basis set, but the geometries virtually stay the same. This highlights the importance the basis sets have on the total energy. From these values, the activation energy can be calculated by taking the difference between the reactant energy and the TS thermal energy. This can be converted to Kcal/mol using the conversion factor 627.509Kcal/mol=1 a.u.

"**Activation energy comparison between chair and boat TS optimisations at the HF/3-21G and B3LYP/6-31G* level**"
'	activation energies	'	'
	T=0K	T=298K	expt T=0K
Chair TS HF/3-21G	45.71	44.70	33.5 ± 0.5
Chair TS B3LYP/6-31G*	27.15	26.29
Boat TS HF/3-21G	55.60	54.76	44.7 ± 2.0
Boat TS B3LYP/6-31G*	41.96	41.32

The different levels of Optimisation lie either side of the experimental value. Therefore taking the average of the lower and higher level basis sets yields a good comparison; for the chair the average at T=0K is 36.43Kcal/mol, and for the boat at T=0K the average is 48.78Kcal/mol. Both these averages are slightly higher than that seen experiementally but are still quite good estimates for the activation energies. They also show how the boat has a higher activation energy than the chair, so is more likely to be the less favourable pathway.

Diels Alder Cylcoaddition

Diels Alder reactions involve the reaction between a diene and a dieneophile with a concerted cyclic transition state. They are [4+2] cycloadditions and hence are a form of pericylcic reaction abiding the Woodward-Hoffmann Rules. This means they are allowed or forbidden depending on their circumstances i.e. thermal or hv. In this case, 4+2 pi electrons leads to a thermally allowed addition via a Huckel, symmetry allowed, pi4s +pi2s transition state. The TS for the reaction between cis-butadiene and ethene, and Cyclohexa-1,3,-diene reaction and maleic anhydride will now be studied to highlight nature of this concerted cycloaddition interaction.

Reaction between cis-butadiene and ethene

Firstly, the reactants were optimised to obtain an image of their MO's.

Cis- butadiene was drawn and optimised in Gaussview. This was done first to the HF/3-21G basis set and then to the B3LYP/6-31G* basis set. The resulting output was then used on an 'energy' calculation at the 6-31G* level to generate the MO's. The final output file can be viewed here: https://www.ch.ic.ac.uk/wiki/index.php/Image:CIS_BUTADIENE_631GMO.LOG

The HOMO and LUMO of cis-butadiene are shown below:

You can see that, with respect to the plane down the middle of the molecule, the HOMO is asymmetric (a) and the LUMO is symmetric (s).

Now, doing the same with ethene, the MO's are:

In this case, you can see the symmetries are reverse: the HOMO is symmetric (s) and the LUMO is asymmetric (a). Therefore, the symmetries of the HOMO's and LUMO's match for both molecules in both directions i.e. the homo of butadine can interact with the lumo of ethene, as can the homo of ethene interact with the lumo of butadiene. So the next thing to look at is the HOMO and LUMO of the TS to see which orbitals really are interacting. A QST3 calculation was run: # opt=(calcall,qst3,noeigen) freq b3lyp/3-21g geom=connectivity and can be found at DOI:10042/to-3537 The optimised reactants and products were used at the B3LYP/631G* level, and then an unoptimised 'TS guess' was inputted, see below.

The TS has some 'long bonds' drawn on it and the product has some bonds 'missing'. This is just due to gaussview playing with the bonds. It does not mean there are bonds in the TS or that there are none in the product. It is just guassview and doesnt affect the calculation. The outcome was:

You can see that the TS did not converge completely to an optimum TS (the bonds are stuck at some energy level:the total energy -233.2747 a.u.) but it is quite close. Therefore, taking this closer TS structure a TS berny calculation was run on it to try optimise it further. The following calculation was run : # opt=(calcall,ts,noeigen) freq am1 geom=connectivity which can be viewed at DOI:10042/to-3538 The resulting structure is:

This is proven as the TS as it has one imaginary vibration at -956cm-1. This vibration corresponds to the vibration at the TS as you can see by the way the molecules move; C3 and C11, and C4 and C14, move concertedly towards and away from each other in a synchronous fashion, see below (LEFT). Comapring this with the lowest possible positive frequency that occurs at 147cm-1 (below-CENTER), the molecules move asynchronously in a twisting fashion, rather than towards each other. This clearly does not correspond to the actual bonding TS vibration but does represent the nature of the final product which itself has a slight twisted kink about this newly synethesised C-C bond (below - RIGHT).

Now looking at the MO's of the TS we can observed which orbitals interact

Now comparing the MO's of the HOMO and LUMO of the TS with the reactants (there are two images of each at different angles to highlight the symmetry).

The HOMO is assymmetric about the plane straight down the middle, and the LUMO is symmetric. This leads to the conclusion that the LUMO of ethene (a) has interacted with the HOMO of cis-butadiene (a) to generate a assymmeetric homo. The reaction is allowed because the symmetries of the orbitals match and the number of electrons favour the Huckel cycloaddtion interaction as already stated in the introduction to this section. To read more about Woodman-Hoffman rules and the stereochemistry of electrocyclic reactions see here ^[1].

Moving on to compare the geometries of the almost optimised TS to the actual TS, you can see there is a slight change in bond lengths and angles

Geometries	Structure	'
bond length/A	TS almost reached	TS
C4-C14	2.29	2.12
C3-C11	2.29	2.12
C2-C4	1.38	1.38
C1-C2	1.41	1.4
C1-C3	1.38	1.38
C11-C14	1.38	1.38
Bond angle/degrees
C3-C1-C2	122.02	121.18
C1-C2-C4	122.02	121.18
C3-C1-C2-C4	0	0

The bond distances between the partially bonding atoms are longer than that of a C-C sigma bond (average C-C bond length = 1.54Å ^[2]), as are the bonds between C1 to C4 longer than the average double and single C-C bonds ( average C=C double bond = 1.34Å ^[3]). This highlights how the structure is still in transition between products and reactants, not quite being a double or a single bond but an intermittant value. The C atom Van der Waals radius is 1.70Å ^[4] If this value was taken to make up a bond then e C-C bond length should be 3.4Å; this is over double the length of a true C-C bond, and is even longer than the long bonds in the TS.

Cyclohexa-1,3,-diene reaction with maleic anhydride

The reaction between Cyclohexa-1,3,-diene reaction and maleic anhydride can undergo two different pathways; the formation of the thermodynamically stable product via a higher energy TS yields the exo product and the kinetically stable product via a lower energy TS yields the endo product, shown below:

The pathway taken is dependent on the angle of attack that the molecules have relative to each other i.e. from above or from below. To Locate these TS's, QST3 will be used, this is most likely to be successful given that it takes into account the reactants, products, and TS, rather than just the TS. Firstly, the reactants and products are optimised using the AM1 semi-empirical approach. these files can be located on D-space:

cyclohexa-1,3,-diene: DOI:10042/to-3539
maleic anhydride: DOI:10042/to-3540
endo product:DOI:10042/to-3541
exo product: DOI:10042/to-3542

A TS guess was drawn for each intermediate. Running the endo product first, the molecules were labelled appropriately and the following calculation was run: # opt=(calcfc,qst3,noeigen) freq am1 geom=connectivity, which can be viewed at DOI:10042/to-3543 Again, the TS guess is in the 3rd window of the image below and the product is in the center due to gaussview's preferences.

The resulting transition structure is shown below with its imaginary vibration at -806.45cm-1. You can see how this vibration moves concertedly, corresponding to the TS vibration.

The input for the exo product was the same as that of the endo and can be viewed at DOI:10042/to-3544 . Again the TS is in the the third window as before, shown below:

The resulting outcome with its imaginary vibration at -812.14cm-1.

This highlights how the exo TS is has a higher energy barrier to overcome to reach the exo product compared to the endo; the exo vibration being at a slightly higher wavenumber, corresponds to shorter wavelength which in turn corresponds to a higher energy vibration.

So now lets look at the orbital overlap of the reactants and see how they compare:

Again, the symmetries of the HOMO's and LUMO's reverse for each reactant allowing HOMO/LUMO interaction in both directions. So lets look at the symmetry of the TS's to see which one do,

Now, both HOMOS and both LUMOs are assymmetric for the endo and exo TS's. So which orbitals combine to form the TS?? Now we must consider the functional groups attached to the reactants. The maleic anhydride has strong electron withdrawing groups attached (carbonyls/oxygen), this will lower the energy of the LUMO, favouring donation into its LUMO rather than donation from its HOMO. This is also reflected in the orbital energy levels taken from the calculation:

Orbital	Reactant	'
	Maleic anhydride	hexadiene
LUMO	-0.05951	0.0168
HOMO	-0.44186	-0.32194

The maleic anhydride lumo is closer in energy with the hexadiene homo than the maleic anhydride homo is with the hexadiene lumo. To conclude, it is safe to safe the LUMO of maleic anhydride interacts with the HOMO of cylclohexadiene to generate the TS MO's. Since the endo is the kinetically more stable product, it has a TS at lower energy than the exo product and hence should exibit better orbital overlap. You can see that there is more electron density on the maleic anhydride oxygen fragment in the endo HOMO compared with the exo HOMO, allowing the large diffuse bonding orbitals of the cyclohexadiene to interact. This is secondary orbital overlap since it is enhancing the likelyhood of bonding even though it is not actually the direct site of sigma bond formation (primary orbital overlap). This secondary overlap is reduced in the exo, the main electron density of the cyclohexadiene being primarily on at the site of siga bond formation. This is further highlighted by viewing the MO's of the TS from the side:

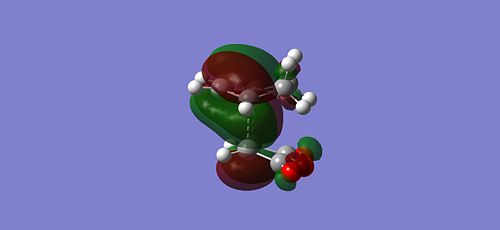Moving on from the MO's, the geometries of the two TS's can also be compared:

Geometry	structure	'	'	'
bond lengths/A	reactants	endo ts	exo ts	product
C6-C17	-	2.16	2.17	1.54
C3-C16	-	2.16	2.17	1.54
C1-C6	1.34	1.39	1.39	1.5
C1-C2	1.45	1.4	1.39	1.5
C2-C3	1.34	1.39	1.39	1.5
C16-C17	1.35	1.41	1.41	1.55
C1-C18	-	2.89	-	2.98
C2-C15	-	3.31	-	3.54
C3-C19	-	2.89	-	2.54
C4-C15	-	-	2.94	2.94
C5-C19	-	-	3.35	3.50
C6-C17	-	-	2.83	2.54
Bond angles/degrees
C1-C2-C3	120.5	118.11	118.11	114.27
C6-C1-C2	120.5	118.11	118.11	114.27

Again, the difference in the C-C is highlighted as you move from reactants to products; the lengths being longer in the transition state and shorter in the reactants and products. This intermitant stage is also observed for the bond angles, the angles reducing considerably from reactants to products, existing at an intermediate transition angle in between. Comparing between the two transition states themselves, the C-C bond lengths are virtually the same. The only place where they vary, which is also highlighted by the difference in secondary orbital overlap, is the distances between the through space carbon framework of the cyclehexadiene that sits ontop of the oxygen network of the maleic anhydride. This distance is slightly longer for the exo TS as the cyclohexadiene bends upwards away from the maleic anhydride and closer for the endo that has favourable secondary orbital overlap in this through space.

Overall, the endo state is favoured over the exo due to a lower energy TS and increased secondary obital overlap. The endo TS is 0.68Kcal/mol more stable in energy than the exo.

References

↑ doi:10.1021/ja01080a054
↑ http://www.tutorvista.com/content/chemistry/chemistry-iii/chemical-bonding/bonding-parameters.php
↑ http://www.tutorvista.com/content/chemistry/chemistry-iii/chemical-bonding/bonding-parameters.php
↑ DOI: 10.1021/j100785a001

[1] :10.1021/ja01080a054

[2] ttp://www.tutorvista.com/content/chemistry/chemistry-iii/chemical-bonding/bonding-parameters.php

[3] ttp://www.tutorvista.com/content/chemistry/chemistry-iii/chemical-bonding/bonding-parameters.php

[4] DOI: 10.1021/j100785a001

[1]

[2]

[3]

[4]