Jump to content

Rep:Mod-YifanDong

From ChemWiki

Transition States and Reactivity

The transition state is a first-order saddle point on the potential energy surface, where it corresponds to a minimum at all points except one (What do you mean "minimum at all points"? Is the potential energy surface flat? I guess that you mean directions instead of point? João (talk) 12:27, 9 February 2015 (UTC)). The Hammond–Leffler postulate states that the transition state resembles either reactants or products (What does that postulate say when the reaction is isothermic? João (talk) 12:27, 9 February 2015 (UTC)). Methods used below are based on this postulate (Why do you think that the methods used are based on the Hammond-Leffler postulate? I don't think they are. João (talk) 12:27, 9 February 2015 (UTC)). The geometries of the transition states are studied computationally using Gaussview.Different calculation methods are introduced and compared. In this exercise, we cover two types of reactions: the Cope Rearrangement and the Diels-Alder reaction.

The Cope Rearrangement

The allowed antiperiplanar and gauche conformations of 1,5-hexadiene are optimized to find the energy-minima and symmetrized to find the point group. The potential energies are calculated using energy optimization to a minimum, the thermochemical data are calculated from a frequency optimization. Usually a combination of OPt+Fre is used.Make sure there is no imaginary frequency.

The Cope Rearrangement

Optimization of Reactants and Products

The conformers of 1,5-hexadiene were optimized to minimum using HF/3-21G method. For each conformer, frequency analysis gives all positive vibrations which indicates it reaches the minimum. The table below shows the conformers and their relative energies. The Gauche 3 conformer is the global minimum (Is this what you expected? João (talk) 19:05, 9 February 2015 (UTC)) because of the attractive interaction between the π orbital and the vinyl protons. However, the energy difference between the gauche3 and anti2 conformations is negligible.[1]

Conformer Structure Energy/Hartrees Relative Energy/kcal/mol Point Group
Gauche 1
Gauche 1
 -231.68772 3.10 C2
Gauche 2
Gauche 2
 -231.69167 0.62 C2
Gauche 3
Gauche 3
 -231.69266 0.00 C1
Gauche 4
Gauche 4
 -231.69153 0.71 C2
Gauche 5
Gauche 5
 -231.68962 1.91 C1
Gauche 6
Gauche 6
 -231.68916 2.20 C1
Anti 2
Anti 2
 -231.69254 0.08 Ci
Anti 3
test molecule
 -231.68907 2.25 C2h
Anti 4
test molecule
 -231.69097 1.06 C1


The Anti 2 conformer was reoptimized using B3LYP/6-31G(d) method.This method gives a lower energy Anti 2 conformer. 6-31G level gives a higher accuracy than the basis set 3-21G. (What is the difference between basis set, method, and level of theory? João (talk) 19:05, 9 February 2015 (UTC))

HF/3-21GFile:C6H10 ANTICi OPT.LOG|; B3LYP/6-31G(d)File:ANTI CI 6-31G(d).LOG

Comparison of different optimisation methods
Method Energy/Hartrees Convergence Jmol
HF/3-21G -231.69254 Item Value Threshold Converged? 
Maximum Force            0.000042     0.000450     YES
RMS     Force            0.000008     0.000300     YES
Maximum Displacement     0.001524     0.001800     YES
RMS     Displacement     0.000749     0.001200     YES
Anti_Ci
B3LYP/6-31G(d) -234.61171 Item Value Threshold Converged? 
Maximum Force            0.000049     0.000450     YES
RMS     Force            0.000008     0.000300     YES
Maximum Displacement     0.001410     0.001800     YES
RMS     Displacement     0.000469     0.001200     YES
Anti_Ci

The table below shows the comparison in bond lengths and bond angles using two methods.It can be summarised from the table that B3LYP/6-31G optimization is closer to the literature values. (Are the literature values other computations or from experiment? It is a good thing that you compared to literature, but how do your two results compare to each other? Are they that different? João (talk) 19:05, 9 February 2015 (UTC))

Geometry comparison of different optimisation methods
Parameters HF-3-21G B3LYP/6-31G Literature
C1=C4 1.3162 1.3382 1.3412
C4-C6 1.5089 1.5074 1.5077
C6-C8 1.5530 1.5549 1.5362
C-H(average) 1.0750 1.0997 1.1077
C1=C4-C6 124.8 122.0 122.5
C4-C6-C8 111.4 112.6 111.0
H-C1=C4 121.9 122.0 120.4
H-C4-C6 115.5 115.5 118.4
H-C6-H 107.7 106.7 107.1
C4-C6-C8-C10(Dihedral angle) 179.99 179.97 179.3

Distances in Å, angles in degrees.

A frequency calculation gives all real and positive vibrational frequencies, which indicates it reaches an energy-minimum. Table below gives the comparison of thermochemistry data using two different optimization methods. (Which of these values do you expect to change with temperature? João (talk) 19:05, 9 February 2015 (UTC))

Thermochemistry data comparison of different optimisation methods
Type of energies Experimental value(B3LYP/6-31G(d))/Hartrees Experimental value(HF/3-21G)/Hartrees
Sum of electronic and zero-point Energies -234.469202 -231.539540
Sum of electronic and thermal Energies -234.461856 -231.532566
Sum of electronic and thermal Enthalpies -234.460912 -231.531622
Sum of electronic and thermal Free Energies -234.500773 -231.570913

Optimisation of the Chair and Boat Transition States

Chair Transition State

In the chair transition structure two optimized C3H5 allyl fragments are positioned approximately 2.2 Å apart, with C2h symmetry. Two different methods are set up to optimize the transition structure: Hartree-Fock(3-21G) where the force constants are computed at the beginning of the calculation and the Redundant Coordinate Editor. (There is a miss-conception here: Hartree-Fock is not a method to calculate transition states, it is a method to calculate electronic energies. You are indeed using two different methods/procedures to calculate the transition state geometry, but in both cases you use the Hartree-Fock method to calculate the necessary electronic energy for each step of the optimization. João (talk) 19:05, 9 February 2015 (UTC))

Hartree-Fock(3-21G) Method
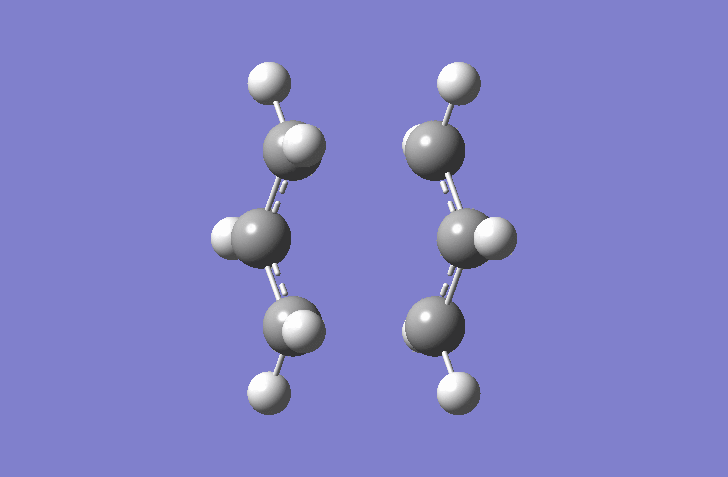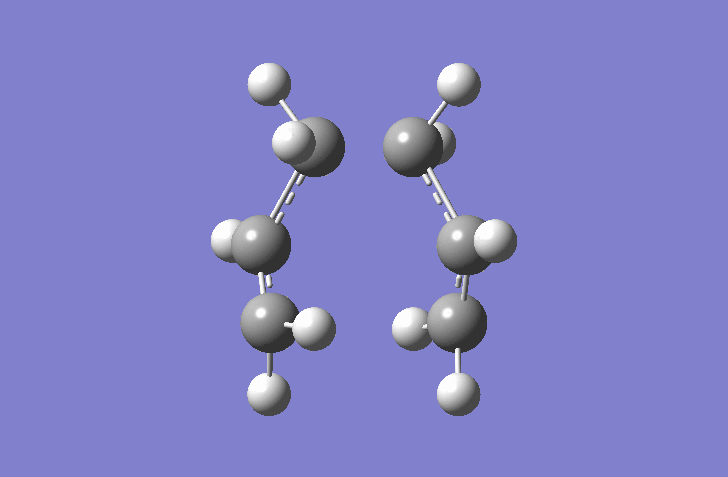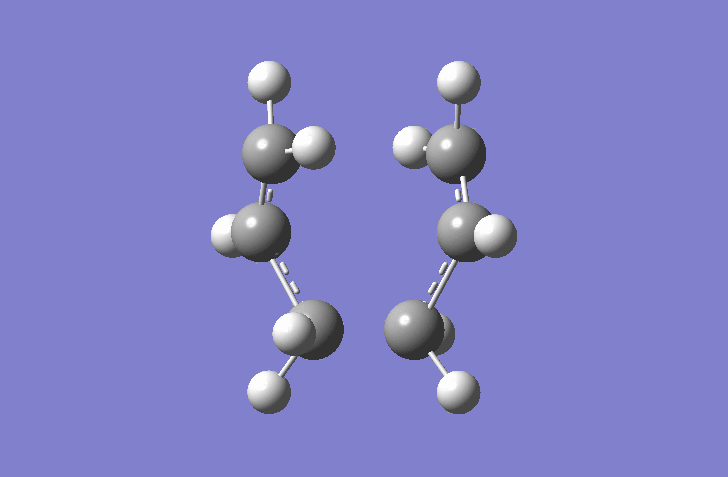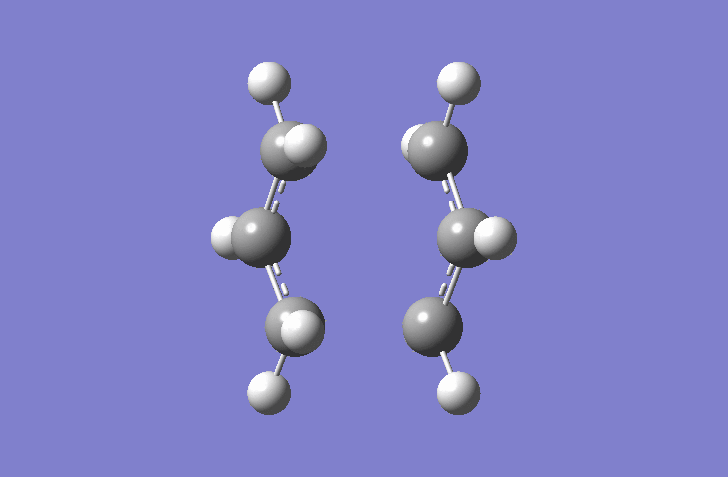
Optimized Chair Transition State Animation using Hartree-Fock Method

In this Hartree-Fock method, a Gaussian optimization was set up as Opt+Fre with Optimization to a TS(Berny). The force constant was calculated once. This stops the calculation crashing if more than one imaginary frequency is detected (This is incorrect, you might have used another keyword to supress this test. João (talk) 19:05, 9 February 2015 (UTC)).The calculation gives an imaginary frequency of -818 cm-1 and a energy of -231.61932 Hartrees.

This method is only used when you have a resonable guess for the transition structure. The optimization is repeated using DFT/B3YLP/6-31G method, which gives an electronic energy of -234.55698 Hartrees and an imaginary frequency of -566 cm-1. (By how much did the geometry change? João (talk) 19:05, 9 February 2015 (UTC))

This is the one corresponding to the Cope rearrangement. ("This is the one" what? João (talk) 19:05, 9 February 2015 (UTC))

Frozen Coordinate Method

This method is used when the guessed structure is far away from the transition structure. (You still need to have some knowledge of the reaction coordinate. João (talk) 19:05, 9 February 2015 (UTC))

The Redundant Coordinate Editor is used to freeze the coordinates. The distance between two of the terminal carbons of the allyl fragments is fixed to be 2.2 Å. The distance between the opposite two of the terminal carbons of the allyl fragments is also fixed to be 2.2Å.

The optimized chair transition structure is like the sturcture optimized using HF/3-21G method, with an electronic energy of -231.69167 Hartrees and an imaginary frequency of -765 cm-1. The two coordinates we differentiate along the path is shown using numerical normal guess Hessian. The newly formed σ C-C bond distance is 1.5509 Å. Compared with the one optimized above using HF/3-21G, this method gives a longer bond forming length. (This bond length actually seems too short for a transition state. I'm not too sure what you are describing here. João (talk) 19:05, 9 February 2015 (UTC))

Optimized Chair Transition State Animation using Frozen Coordinate Method with Modified Heissan. (What exactly is this animation showing? João (talk) 19:05, 9 February 2015 (UTC))

Boat Transition State

In the boat transition structure two allyl fragments are positioned 2.2Å apart, with C2v symmetry (In this method you start with two structures that resemble your product and reactants. Each of these would be a hexadiene structure and not two allyl groups in close proximity. Further, do they really have C2v symmetry? João (talk) 19:05, 9 February 2015 (UTC)). The structure is optimized using QST2 method, where the calculation will interpolate between reactants and products and locate a transition state in between them. This method would fail if the reactant and product structures are not close enough to the transition state structure.

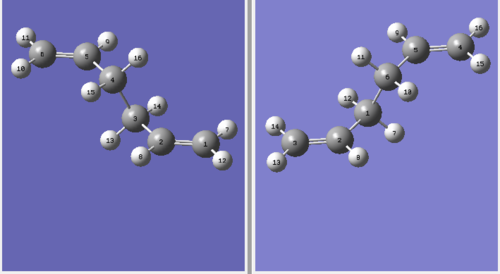
Reactant and Product with Labelled Atoms

The structure above is like a more dissociated version of the chair transition structure (The structure above does not show this. João (talk) 19:05, 9 February 2015 (UTC)). The limitation of QST2 method is that the job is only successful when the input file includes a structure closer to the boat transition structure. In order to optimize the transition state the structure is modified as shown below.


Reactant and Product with Labelled Atoms and Modified Arrangements

(Did you find a transition state structure? How did you confirm it was a transition state? João (talk) 19:05, 9 February 2015 (UTC))

Further improvement: QST3 method is more reliable than QST2 because it allows you to input the guessed transition structure.

Intrinsic Reaction Coordinate

IRC method calculates the minimum energy path from a transition state structure to the local minimum (What happens if there is a local minimum along the path? João (talk) 19:05, 9 February 2015 (UTC)). Since the reaction is symmetrical, the reaction coordinate is computed only in the forward direction. If given an unsymmetrical reaction then the reaction coordinate will be computed in both directions. As the frequency calculation was previously computed, we calculate the force constants once, rather than at every step along the path. This IRC method gives an electronic energy of -231.69153 Hartrees. The animation is shown below.


Optimized Chair Transition State using IRC method

The IRC method didn't give a minimum geometry (What happened? João (talk) 19:05, 9 February 2015 (UTC)). It only gives the direction where the slope of the potential energy surface is steepest. The chair transition structure is re-optimized using two approaches listed below. (Why do you want to reoptimize the chair transition structure, isn't that the structure you started with? João (talk) 19:05, 9 February 2015 (UTC))

(1)Minimization for the last point on the IRC Minimization of the last point on the IRC gives an electronic energy of -231.69167 Hartrees. This approach requires the structure close to the chair transition state, otherwise it will give a wrong minimum.

(2)Change the number of points along the IRC to a higher number until it reaches a minimum.From the table, we can tell that an increase in number of points leads to a a slightly lower energy. (The energy is actually the same in all cases. Do you think that the number of steps actually made in each calculation is actually different? João (talk) 19:05, 9 February 2015 (UTC))

Optimization along the IRC
Number of Points Electronic Energy
100 -231.69158 Hartrees
150 -231.69158 Hartrees
200 -231.69158 Hartrees

Summary of Results

The table below shows the comparison of activation energies in HF/3-21G and B3LYP/6-31G. (What do you conclude from this table? João (talk) 19:05, 9 February 2015 (UTC))

Summary of Activation Energies(in kcal/mol)
Terms HF/3-21G HF/3-21G B3LYP/6-31G B3LYP/6-31G Experimental Value
at 0K at 298.15K at 0K at 298.15K at 0K
ΔE(chair) 45.71 44.70 34.07 33.16 33.5±0.5
ΔE(boat) 55.60 54.76 41.96 41.32 44.7±2.0


The table below shows the thermochemical data for chair and boat transition structures.

Summary of Energies(in Hartreers)
HF/3-21G B3LYP/6-31G*
Electronic energy Sum of electronic and zero-point energies Sum of electronic and thermal energies Electronic energy Sum of electronic and zero-point energies Sum of electronic and thermal energies
at 0K at 298.15K at 0K at 298.15K
Chair TS -231.61932 -231.46670 -231.46134 -234.55698 -234.41491 -234.40898
Boat TS -231.60280 -231.45093 -231.44530 -234.54308 -234.40236 -234.39601

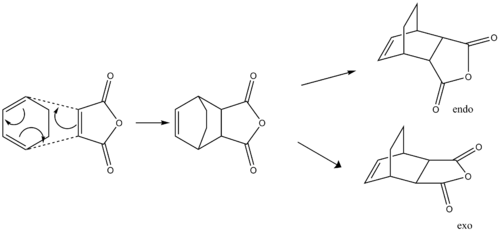
The Diels Alder Cycloaddition

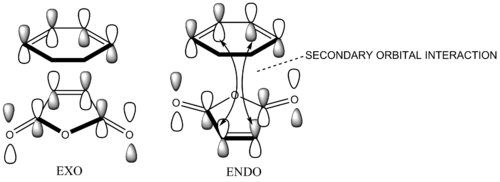
Diels-Alder is a [4+2] cycloaddition reaction. Diels-Alder reactions occur between a conjugated s-cis diene and a dienophile. In this exercise, the reaction between maleic anhydride and cyclopentadiene (Cyclohexadiene actually. João (talk) 19:05, 9 February 2015 (UTC)) is studied. The less stable product, the endo product is formed in the irreversible Diels-Alder reactions. The kinetic product is formed faster because the bonding interaction in transition state between the electron-deficient C=O groups and back of the diene lowers the energy of its transition state.

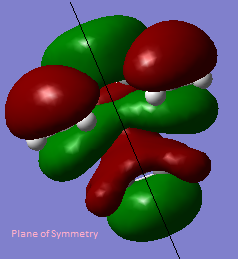
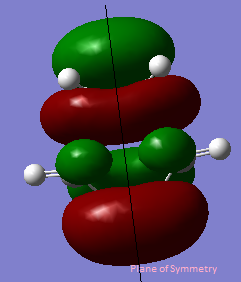
The HOMO and LUMO interact when there is a significant overlap between them.They must have the same symmetry for a good overlap. In the cis-butadiene and ethylene cycloaddition, the HOMO of ethylene and the LUMO of cis-butadiene are both symmetric with respect to the plane, the LUMO of ethylene and the HOMO of cis-butadiene are both antisymmetric with respect to the plane.

Optimisation of Cis-Butadiene and Ethylene

The table below shows the HOMO and LUMO of cis-butadiene and ethylene.The structures are optimized using Hartree-Fock/3-21G method and the MOs are visualized with an isovalue of 0.02.

HOMO and LUMO of Transition Structures
Cis-Butadiene Ethylene
Term Molecular Orbitals Symmetry Term Molecular Orbitals Symmetry
LUMO 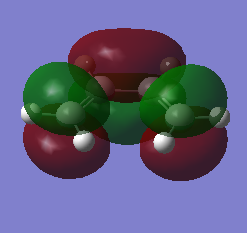Symmetric LUMO 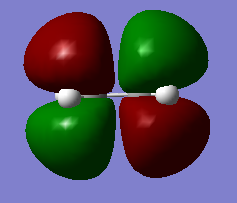Anti Symmetric
HOMO Anti symmetric HOMO 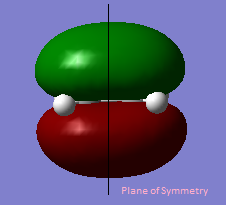Symmetric

Computation of the Transition State Geometry

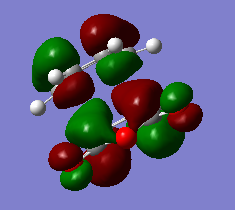
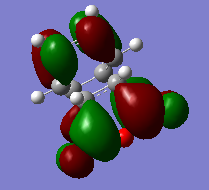
The Hartree-Fock/3-21G method gives an imaginary frequency of -818 cm-1. AM1 Semi-emipirical method gives an imaginary frequency of -956 cm-1. The presence of an imaginary frequency indicates a negative secondary derivative, which corresponds to the transition state. The animation above corresponds to the reaction path,we can tell from it that the formation of the two bonds is synchronous. Therefore the reaction is allowed under Woodward-Hoffman Rule. From the MOs of the transition states we can tell LUMO of ethylene and HOMO of cis-butadiene interact constructively to give an antisymmetric HOMO.HOMO of ethylene and LUMO of cis-butadiene interact to give a symmetric LUMO.

HOMO and LUMO of the transition states are shown below.

HOMO and LUMO of Prototype Reaction Transition Structure
HF/3-21G AM1 Semi-Empirical
Term Molecular Orbitals Symmetry Relative Energy Term Molecular Orbitals Symmetry Relative Energy
LUMO Symmetric 0.14241 LUMO Symmetric 0.02315
HOMO Symmetric -0.30087 HOMO AntiSymmetric -0.32394

MOs are visualized with an isovalue of 0.02 in both methods. (I think the differences in the HOMO obtained with the two methods deserves a comment. João (talk) 19:05, 9 February 2015 (UTC))

A typical sp3 C-C bond distance is 1.54 cm. A typical sp2 C-C bond distance is 1.50 cm-1.[2] The van der Waals radius of the C atom vibration is 1.7 Å.[3] The bond length of the partly formed C-C bond is 2.20 Å which is longer than the normal sp3 C-C bond distance and the van der Waals radius (But it is crucially smaller than twice the van der Waals radius of carbon João (talk) 19:05, 9 February 2015 (UTC)).This is because at transition state the bond is still being formed. The bond length in the original ethylene is now 1.39Å. The original C=C bond in cis-butadiene is now 1.40 Å and the original C-C bond in the cis-butadiene is now 1.41 Å.This indicates a delocalization of electrons in the transition state.

Regioselectivity of the Diels Alder Reaction

The kinetically controlled reaction between cyclohexa-1,3-diene and maleic anhydride is studied by guessing and optimizing its transition state using the method we introduced above. The corresponding energy for each conformation is calculated using Gaussview. The major product formed is the endo product (Does your calculation actually tell you this? Under which conditions is your statement true? João (talk) 19:05, 9 February 2015 (UTC)). The endo rule is explained computationally.

Diels Alder Reaction between Cyclohexa-1,3-diene and Maleic Anhydride

HOMO and LUMO of Transition States

The transition structure is optimised using AM1 Semi-empirical method. The reaction path is shown in the animation below. (The imaginary frequency mode at the transition state structure gives you an indication of the reaction path, but only in the vicinity of the transition state. João (talk) 19:05, 9 February 2015 (UTC))


ENDO and EXO Transition States
Term ENDO EXO
Transition Structure
ENDO
EXO
Energy -0.051505 Hartrees -0.050419 Hartrees
Imaginary Frequency -806 cm-1 -812 cm-1

The less stable product, the endo product is the major product in this irreversible Diels-Alder reactions. Besides the usual primary interaction, there is an additional bonding interaction between the electron-deficient C=O groupes and back of the diene.This interaction is known as a secondary orbital interaction, which lowers the transition state energy of end product relative to the exo product.[4] (Does your calculation show evidence for this effect? Is there any other effect playing a role? João (talk) 19:05, 9 February 2015 (UTC))

Secondary Orbital Interaction


HOMO and LUMO of ENDO and EXO Transition States
ENDO EXO
Term Molecular Orbitals Symmetry Relative Energy Term Molecular Orbitals Symmetry Relative Energy
LUMO Antisymmetric -0.03570 LUMO Antisymmetric 0.00601
HOMO Antisymmetric -0.34505 HOMO Symmetric -0.38787

Intrinsic Reaction Coordinate Calculation

IRC and RMS Gradient of ENDO and EXO Conformations
Term ENDO EXO
IRC path
RMS Gradient
Relative Energy of Transition State/Hartrees -0.051505 -0.050420
Relative Energy of Product at IRC=-5.9/Hartrees -0.15985 -0.15991

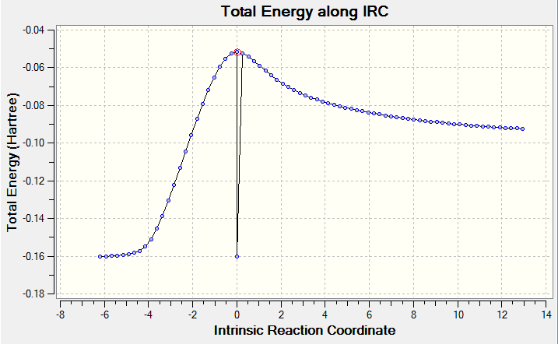
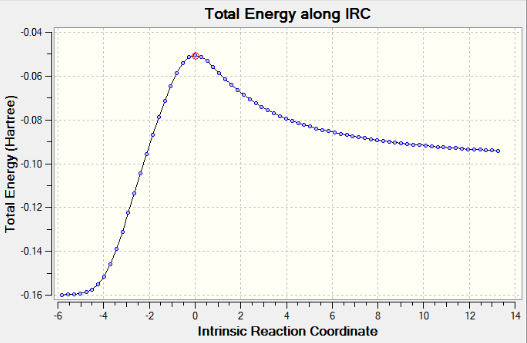
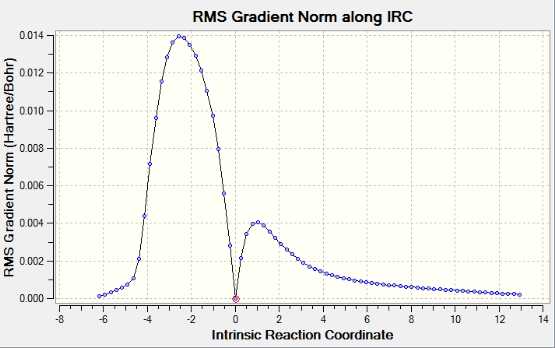
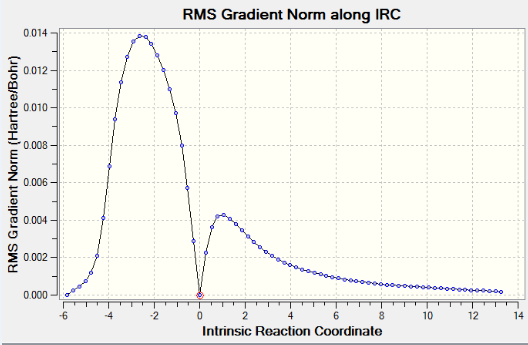
AM1 method gives an IRC path which resembles the path going from product(on the left) to reactants(on the right). The reactants tend to be far away from each other therefore the calculation does not converge.A weird point on the IRC curve is observed after the transition state, where it suddenly drops to the product. However, this point does not show up in the corresponding RMS gradient curve. IRC curve proves the optimized transition structures for endo and exo products are correct. A correct optimized transition structure has a gradient of 0 with an imaginary frequency.

Further Discussion

In the optimization of transition state study, solvent effect is neglected.[5]

References

<references> Template loop detected: Template:Reflist [1]

<references> [6]

  1. ↑ 1.0 1.1 Conformational Study of 1,5-Hexadiene and 1,5-Diene-3,4-diols,http://pubs.acs.org/doi/abs/10.1021/ja00111a016.
  2. ↑ Bond lengths in organic compounds',Frank H. Allen, Olga Kennard, David G. Watson, Lee Brammer, A. Guy Orpen and Robin Taylor J. Chem. Soc., Perkin Trans. 2, 1987, S1-S19,http://pubs.rsc.org/en/content/articlepdf/1987/p2/p298700000s1.
  3. ↑ van der Waals Volumes and Radii; A. Bondi, J. Phys. Chem., 1964, 68 (3), pp 441–451 DOI: 10.1021/j100785a001.
  4. ↑ Ian Fleming, Molecular Orbitals and Organic Chemical Reactions,ISBN 978-0-470-74658-5
  5. ↑ M. F. Ruiz-Lopez , X. Assfeld , J. I. Garcia , J. A. Mayoral , L. Salvatella,J. Am.Chem. Soc., 1993, 115 (19), pp 8780–8787DOI: 10.1021/ja00072a035
  6. ↑ Bond lengths in organic compounds,Frank H. Allen, Olga Kennard, David G. Watson, Lee Brammer, A. Guy Orpen and Robin Taylor J. Chem. Soc., Perkin Trans. 2, 1987, S1-S19,http://pubs.rsc.org/en/content/articlepdf/1987/p2/p298700000s1.

[1]

  1. ↑ van der Waals Volumes and Radii; A. Bondi, J. Phys. Chem., 1964, 68 (3), pp 441–451. DOI:10.1021/j100785a001

[1]

  1. ↑ Ian Fleming, Molecular Orbitals and Organic Chemical Reactions,ISBN 978-0-470-74658-5

[1]

  1. ↑ M. F. Ruiz-Lopez , X. Assfeld , J. I. Garcia , J. A. Mayoral , L. Salvatella,J. Am.Chem. Soc., 1993, 115 (19), pp 8780–8787.DOI:10.1021/to-ja00072a035 .
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod-YifanDong&oldid=815367"