Rep:MgoSHAY123

The Free Energy and Expansion of MgO

Abstract

In this experiment, various methods were used to compute the free energy and expansion coefficient of an MgO crystal. The optimum grid size in terms of speed of calculation vs accuracy was found to be a grid of 16x16x16 primitive unit cells of MgO. The quasi-harmonic approximation was the more accurate method to determine the Helmholtz free energy and lattice volume at low temperatures, whereas using molecular dynamics was the more appropriate at higher temperatures.

Introduction

The systemː MgO crystal

The experiment was conducted on a crystal of MgO, which takes the form of a face-centred cubic lattice. The grid size 1x1x1 represented one primitive unit cell of MgO, containing two atoms. A 2x2x2 grid consisted of four unit cells of MgO (8 atoms) and so on. The grid size was varied throughout the experiment.

The methods

The quasi-harmonic approximation

One of the approximations in this method is that the motions of the particles are harmonic and its energy vs displacement graph has a parabolic form, i.e. that the motions lie within the equilibrium region of the Lennard-Jones potential, which can be approximated as a parabola.

This method can be used to compute the vibrational modes (otherwise known as the phonon modes) of the lattice, represented by dispersion curves. Dispersion curves illustrate the branch nature of vibrational continua present in the structure and have an origin Γ. The density of states of these modes within the branches can also be calculated. The density of states represents the number of levels at a particular k-point in reciprocal space and each energy level has a corresponding value of k. The displacement a (the lattice constant) within a lattice relates to a position k in reciprocal space by k=2π/a. In a dispersion curve the levels are equally spaced along the k axis, thus, the steeper the gradient, the fewer vibrational levels can be accommodated, resulting in a lower density of states.

The quasi-harmonic approximation was also used to optimise the structure in order to determine the coefficient of thermal expansion, α, with respect to the free energy of the structure. Equation 1 relates the volume of the unit cell to the temperature and can be used to determine a value of α.

Equation 1

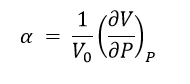
Molecular dynamics

The molecular dynamics method simulates the random nature of the particle motions. It contains a timestep parameter which allows the forces on the atoms to be computed using classical Newtonian mechanics in real time and updates the velocities and positions of the particles for the next calculation. The method follows an algorithm which sets the particles moving randomly, accelerates them according to F=ma and adjusts their velocities and positions for the next step in the calculation. This process is repeated for a desired number of timesteps.

The software

The numerical calculations were carried out using a graphical user interface called DLVisualise within RedHat Linux.

Results

Calculating the phonon modes of MgO

Figure 1: Phonon dispersion curves

The density of states for the 1x1x1 grid can be found in Figure 2. According to the phonon dispersion curve (Figure 1), this corresponds to the k-point L. L contains six bands, including two sets of degenerate bands which account for the peaks at ~280 cm^-1 and ~350 cm^-1 being twice as high as the other two peaks, as there are twice as many states within those bands.

The curve for the density of states gains more features as the grid size increases but eventually becomes a smoother curve with fewer new features appearing. As the structure gets larger, it converges to simulating an infinite lattice, with the vibrations at the edge of the lattice becoming negligible with respect to those of the bulk material.

The difference between the density of states graph is least significant between the 16x16x16 grid and the 32x32x32 grid and what we gain in accuracy from the larger grid, we lose in speed of calculation, as the 32x32x32 calculation took more time. Hence, the 16x16x16 grid is sufficient for a reasonable approximation to the density of states.

This grid size would also be appropriate to use with another metal oxide such as CaO, as the ions carry the same charges so the interactions can be treated similarly and the unit cells contain the same number of atoms. However, another optimum grid size would have to be found for a zeolite like faujasite, as the lattice does not have an FCC configuration. This grid size would not be optimal for a metal such as lithium as the interactions are not comparable to that of MgO as there is only one type of atom.

Figure 2: Density of states (Top: 1x1x1, 2x2x2, 4x4x4. Bottom: 8x8x8,16x16x16, 32x32x32)

Computing the free energy

Figure 3: Free energy vs grid size at 300 K

The grid size of MgO was varied and the Helmholtz free energy was computed within the quasi-harmonic approximation (see Figure 3). Initially, as the grid is enlarged, the free energy decreases but then increases from the 4x4x4 grid upwards. The magnitude of ΔE decreases with increasing grid size, indicating that the value is converging to the free energy of an infinite lattice.

The grid size used can be selected according to the desired degree of accuracy. For example, a 1x1x1 grid would be sufficient in calculations correct to 1 meV, as using a 2x2x2 increases the accuracy by <0.005 eV. Similarly, for accuracies of 0.5 meV and 0.1 meV, 2x2x2 and 4x4x4 grids can be used, respectively.

Thermal expansion coefficient

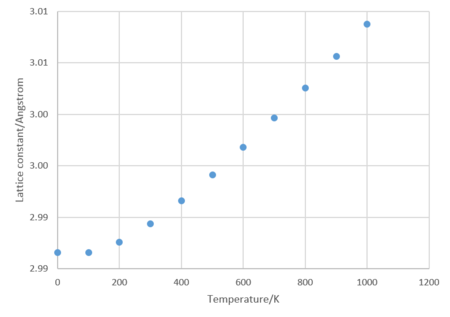
Again, within the quasi-harmonic approximation, the Helmholtz free energy and lattice constant for temperatures between 0 and 1000 K were calculated and plotted in Figures 4 and 5. Both graphs have a linear region >300 K and are curved below this temperature.

The coefficient of thermal expansion, α, was found to be 2.65x10^-5 K^-1. In literature, the coefficient of thermal expansion at 300 K was 2.88x10^-5 K^-1. This is the same order of magnitude and similar in value to that of this experiment.

The curved region appears as a result of quantum mechanical properties, specifically the zero point energy, which is the energy that a system possesses at 0 K. Had these effects not been taken into account, the graph would be linear.

Figure 4: Free energy vs temperature

Figure 5: Lattice constant vs temperature

Molecular dynamics (MD) calculations

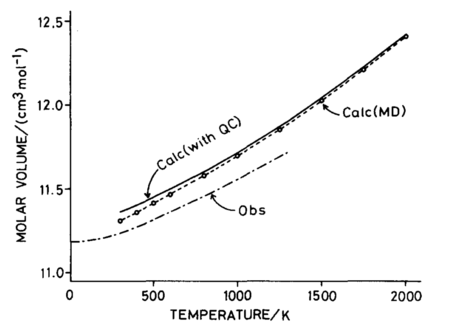
The MD calculations were conducted on an MgO superlattice of 32 MgO units. Figure 6 contains the results from the MD simulations alongside that of the quasi-harmonic approximation. It can be seen that the MD points are entirely linear, as opposed to becoming curved at lower temperatures as with the quasi-harmonic approximation.

In literature, the relationship observed experimentally matches that of the quasi-harmonic approximation (see Figure 7) as opposed to MD, suggesting that the quasi-harmonic approximation is more accurate at lower temperatures. The MD simulation is purely classical and does not take into account the zero-point energy that the quantum-harmonic approximation does.

However, at higher temperatures, the MD method is more accurate as it supplies the atoms with energy corresponding to a certain temperature and hence adjusts the motion of the atoms accordingly. These motions may be anharmonic at high temperatures due to phonon interaction. The quasi-harmonic approximation does not take into account this anharmonicity so cannot simulate structures at high temperatures.

Figure 6: Free energy vs temperature

Figure 7: Masanori Matsui's Molecular dynamics study of the structural and thermodynamic properties of MgO crystal with quantum correction

Conclusion

From this experiment, the following conclusions can be drawn:

• The quasi-harmonic approximation was suitable for computing the coefficient of thermal expansion as the value obtained was comparable to that found in literature.

• The 16x16x16 grid was optimum as it provided a compromise between speed of simulation and the accuracy of the calculation with respect to the infinite lattice.
• Both methods have their flaws; the quasi-harmonic approximation fails at higher temperatures due to motions becoming anharmonic, and molecular dynamics is not appropriate for use at lower temperatures, as it is a purely classical approximation and cannot take into account quantum mechanical properties of the material.