Introduction

Magnesium oxide naturally exists as crystal based on face-centred cubic lattice with the lattice points taken by Mg²⁺ and the octahedral holes filled with O^2-.

Type of Unit Cell	Shape	Parameter	Internal Angel	Volume	Number of MgO
Conventional	Cube	a_c = b_c = c_c = 4.212 ‎Å	α_c = β_c = γ_c = 90^•	V_c = 74.725 Å³	N_c = 4
Primitive	Rhombohedron	a_p = b_p = c_p = 2.978 ‎Å	α_p = β_p = γ_p = 60^•	V_p = 18.6812 Å³	N_p = 1

Vibrations of a solid system are related to many of its physical properties such as free energy, heat capacity, expansion, phase transition, thermal conductivity and dielectric phenomena at low frequencies. This study compares two methods for simulation of MgO crystal vibrations. The quasi-harmonic approximation (QH) considers vibrations as phonons representing elementary vibrational modes in which a lattice of particles uniformly oscillates at a single frequency. The molecular dynamics (MD) allows the particle in the system to interact for a given time period and the coordinates of the particles are numerically solved based on Newton's Laws R_final = R_initial + v_final*dt = R_initial + v_initial*dt + a*dt² = R_initial + v_initial*dt + (F/m)*dt². Both methods were conducted on Linux based programme GULP (General Utility Lattice Program) via the user interface for constructing and visualizing provided by DL Visualize.

Theory

In statistical mechanics, the physical properties of a system are in Boltzmann Distribution n_i / N = exp (-βu_i) / q where β = 1 / (k_bT) and q = Σ_j=1^levels exp (-βu_j). This means that once the partition function q is correctly expressed, the properties of the system can be calculated.² For example in this experiment, in accordance with harmonic oscillation model, the vibrational frequency ω must be quantised and summing over the frequencies will lead to the partition function, and the Helmholtz free energy A can be obtained using A = E₀ + 1/2 Σ_j,kћω_j,k + k_bT*Σ_j,kln[1-exp(-ћω_j,k/k_bT)]

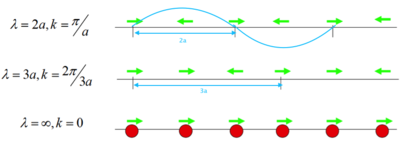
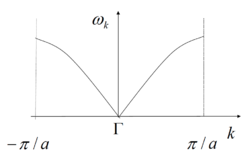
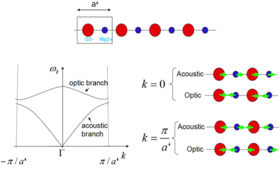
MgO crystal is made of repeating unit cells, so it is sensible to start with the simplest model first to see how frequency ω is related to the repeating structure. When a 1-dimensional chain of one kind of atom vibrate, they can have several different states of vibrations and each one can be described as a wave with a wavelength equal to the length of the repeating unit (Fig.2) and plotting the vibrational frequencies VS the k-vectors (showing directions and wavelengths of vibrations) gives a graph like Fig.3. If each atom in this chain is superseded by a MgO, there is now a pair of ions in each repeat unit, a' = 2a, hence -π/(2a) < k < π/(2a) and folding branch occurs (Fig.4).

Fig¹.2 1D vibrations; wave vector k = 2π / λ; -π/2 < k < π/2; frequency ω increases as k increases.	Fig¹.3 typical ω(k) is plotted as a dispersion curve; k = 0 at Γ point	Fig¹.4 1D MgO chain; There exists two frequencies for one k-vector due to the two types of oscillations between Mg₂₊ and O_2-. The same reason causes the gap between the acoustic branch and the optical branch.

Both structures mentioned above are limited in 1 dimension. When the structure is expanded to two dimensions, particles can vibrate up and down with respect to the horizontal axis more than just along the axis, hence k-vectors are expressed as (k_x, k_y) in a Cartesian coordinate system, and the ω(k) plot becomes a dispersion surface with frequency ω showed in z-axis. It is now easy to see that for 3-dimensional MgO crystal, k points includes (k_x, k_y, k_z), and there will be four Cartesian axises for a ω(k) plot, which is not able to show in real life. In this case, a certain path in the 3-dimensional solid is set and the coordinates through the path are set as the k points, thus ω(k) can be plotted against the path and it is again back to the dispersion curve.

Once the all the vibrational branches are obtained, sum over them to form the partition function, hence the Helmholtz free energy and the cell volume.

Results and Discussion

Error creating thumbnail: File with dimensions greater than 12.5 MP

Fig.5 Dispersion Curve of MgO lattice vibrations; path W-L-Γ-W-X-K on horizontal axis with coordinates shown in blue

The lattice energy of MgO calculated is -41.075 eV, and this is the potential energy holding the lattice together induced by electrostatic interaction between Mg₂₊ and O_2- ions, which means to move all the ions in the lattice apart to infinity requires an energy of 41.075 eV (lit³.41.197 eV). Also, this equals to the internal energy of an ideal MgO lattice as perfect crystals have no vibrations, but ions in the real solid crystal do not stay still.

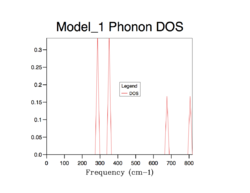
As mentioned in the theory part, to understand the variation of vibrational frequencies with k, a dispersion curve is essential. To deal with the 3-dimensional MgO infinite lattice, a conventional path in the k-space is used to compute the vibrational modes, and for Fig.5, 50 points along the path was computed and shows all the phonon modes.

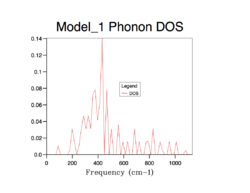
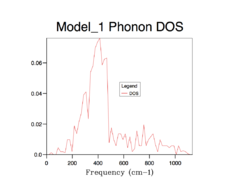
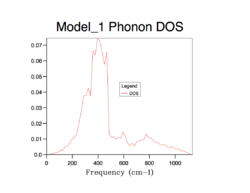
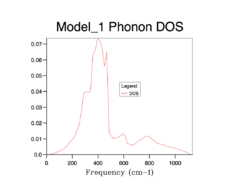
The strategy to sum up the phonon modes is to construct the Density of Sate (DOS), indicating the probability of a phonon to be in a certain state (i.e. frequency). It is important to sum up phonons for an adequate number of k points so that the distribution of them can be represent the distribution of phonons of an infinite lattice. The following shows the process of finding the best number of k points for computing DOS.

Shrinking Factor	Density of State	Comments
1		The DOS for 1x1x1 grid was computed for a single k-point 'L'. There are 4 distinct peaks, the two around 300 and 400 cm^-1 is double in intensity compared to the 700 and 800 cm^-1, which is corresponding to the two branches across point 'L' shown in the dispersion curve. summing over more k points to get a distribution
2		7 distinct peaks, highest peak at 400 cm^-1 lower density of each peaks compared to the DOS above A grid size of 222 is sufficient to get the correct highest value. summing over more k points to get a distribution
4		more peaks, highest peak at 400 cm^-1 with lowered density not a smooth distribution yet
8		highest peak at 400 cm^-1 with even lowered density Distribution features appear. large fluctuations
16		a general shape of the distribution with small fluctuations no much change in the densities
32		nice distribution compared to the upper one acceptable computation time
64		There is no much change compare to the DOS computed along grid 323232, however takes a few minutes longer to compute. The DOS is converging which means it is converging.

As the grid size increases, more possible vibrations are sampled and the distribution is smoothened, nevertheless, the change in DOS decreases each time the grid size is doubled. Computing over more k-points requires more resources and time, which is obvious from grid 32*32*32 to 64*64*64. A compromise can be grid 32*32*32 which can give a good enough distribution as a close approximation to the infinite lattice economically.

Since there is a way (the quasi-harmonic approximation) to compute all the phonon modes in MgO infinite lattice, the free energy of it can also be calculated, and GULP is able to search for the minimum free energy with respect to the structure via calculating the internal energy and phonons at a sequence of geometries. Similarly, the computing path in k-space is the same as that for computing DOS, so there is also the grid size problem.

Shrinking Factor	Helmholtz Free Energy (eV)	Accuracy
1	- 40.930301	100 meV
2	- 40.926609	1 meV
3	- 40.926432	0.5 meV
4	- 40.926450	0.1 meV
5	- 40.926463
6	- 40.926471
7	- 40.926475	0.01 meV
8	- 40.926478
9	- 40.926479
10	- 40.926480
11	- 40.926481	convergence
12	- 40.926481

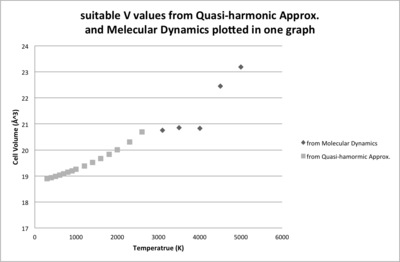
A grid size of 11*11*11 was chosen for the following calculations based on the QH method. The Helmholtz free energy and the cell volume were optimised to observe the variations with different temperature. As temperature is raising, the Helmholtz Free Energy becomes more negative, while the cell volume is expanding, Both of the variations can be well expressed by polynomial equations. Calculation failed when temperature is close to the melting point of MgO (lit⁴. 3125 K). The reason could be the vibrations was so large that atoms clashed into each other causing computing errors.

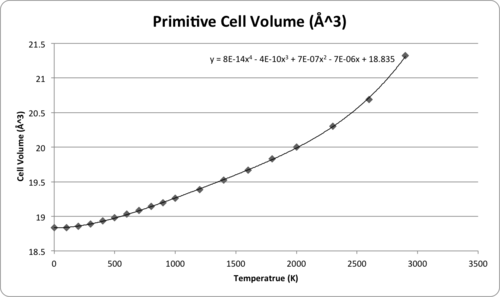
Temperature (K)	Helmholtz Free Energy A (eV)	Lattice Volume (Å³)
0	-40.9019	18.8365
100	-40.9024	18.8383
200	-40.9094	18.8562
300	-40.9281	18.8900
400	-40.9586	18.9325
500	-40.9994	18.9801
600	-41.0493	19.0312
700	-41.1071	19.0851
800	-41.1719	19.1413
900	-41.2430	19.1997
1000	-41.3110	19.2601
1200	-41.4887	19.3872
1400	-41.6755	19.5233
1600	-41.8780	19.6698
1800	-42.0944	19.8287
2000	-42.3237	20.0029
2300	-42.6895	20.3047
2600	-43.0800	20.6889
2900	-43.4948	21.3217

In order to compare the computing thermal expansion with the literature values, several cell volumes were obtained by substituting some specific temperatures into the trend line equation in Fig.7, and the predicted cell volumes were then transferred into molar volume by multiplying Avogadro constant N_A with the units changed to what is used in the literature.

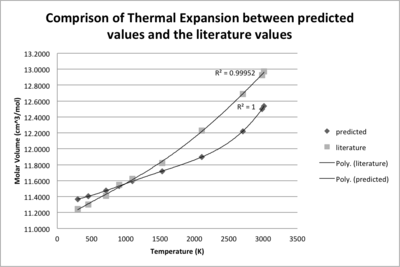
Temperature (K)	Cell Volume (Å³)	Molar Volume (cm³mol^-1)	Literature5^{Molar Volume (cm³mol^-1)}
298	18.8851	11.3688	11.2434
455	18.9425	11.4034	11.3004
710	19.0601	11.4742	11.4109
1096	19.2570	11.5927	11.6211
1527	19.4673	11.7193	11.8218
2106	19.7624	11.8970	12.2287
2703	20.3014	12.2214	12.6887
2986	20.7658	12.5010	12.9244
3015	20.8248	12.5365	12.9723

As mentioned in the introduction part, another simulation method MD was also used to calculate the equilibrium energy and volume. The MD obtained values before the melting point of MgO are similar compared to those obtained by QH, and after the m.p., MD can compensate the failure of QH. Around the m.p., there is a range where the volume almost keeps constant, indicating phase changing. When T reaches 4000 K, the volume is lifted by more than 10 Å³ higher, indicating phase change is completed and the volume of liquid phase will continue increase with the raising temperature but with a steeper gradient. If the temperature goes on increasing, the volume will become infinite as the gas phase does not have a volume without any pressure.

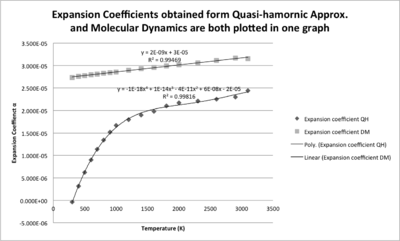
The change of cell volume can be describes as thermal expansion coefficient α_V=(1/V₀)(dV/dT). This property can be calculated for both of the data sets obtained from different methods, and V₀ is the zero-point volume in each case and the (dV/dT) is the gradient of the trend lines.

Fig.9 suitable V values from the QH and MD plotted in one graph	Fig.10 Comparison between α_V obtained from different methods. It can be concluded that the difference is decreasing from low temperature to 1500 K after which the difference in expansion coefficient tends to keep constant.

Conclusions

This experiment found that the cell volume (i.e. the separations) of MgO crystal increases with the rising temperature, and this causes the thermal expansion. The original of thermal expansion is the anharmonic vibrations due to the asymmetric interatomic potential. The QH method assumes that all the vibrations are harmonic so the cell volume will not change much, but it is true only when the temperature is relatively low; while the MD method is closer to the real life but less economic, it should be used for simulation of vibrations at higher temperature.

To use statistic method to study a system needs a large enough ensemble, or else the average property will not be a good approximation.

Reference

1. Prof N. M. Harrison’s Lectrure Notes: Vibrations in crystals

2. J. M. Seddon and J. D. Ga, Thermodynamics and Statistical Mechanics, the Royal Society of Chemistry, Cambridge, 2001

3. B. K. Vainshtein, V. M. Fridkin and V. L. Indenbom, Modern Crystallography 2: Structure of Crystals, Springer, London, 3rd Edn., 2000, pp. 64.

4. Chemistryworld, http://www.rsc.org/chemistryworld/2014/08/magnesium-oxide-mgo-podcast, (accessed Nov. 2015)

5. L.S. Dubrovinsky and S.K. Saxena, Phys Chem Minerals, 1997, 24: 547–550