Rep:MOD:tyl214

Transition State Computational Lab

Introduction

Whilst stereo-selectivity is one of the biggest challenges in synthetic chemistry, a better understanding of the transition state in a reaction would allow better synthetic routes. In this computational lab, GaussView 5.0 was used to perform simulations of different cycloaddition reactions. Both the semi-empirical/PM6 and B3LYP/6-31G(d) basis sets were used, where the PM6 method is based on experimental data and the 6-31G(d) originates from the Density Functional Theory (DFT).
In a chemical reaction, there are always 3N-6 degree of freedoms. In order to extract information from the Potential Energy Surface (PES), we tend to fix all coordinate apart from one. In this computational lab, we are fixing all coordinates to a minimum apart from the reaction coordinate, where the transition state can be found at the maximum of the reaction coordinate. This is done by calculating the first and second derivatives of energy against the reaction coordinate. Note that since the maxima of a curve has a negative second derivative, therefore any transition state optimisations will give rise to a vibration at negative frequency, depicting an imaginary frequency.

Nf710 (talk) 20:28, 16 April 2017 (BST) You are along the right lines , but fixing is the wrong word. you look for all points with first derivatives of zero with respect to the normal modes. The TS sis the the point where the second derivatibe wrt to the normal mostes is positive in all directions but 1 the reaction co-ordinate.

Exercise 1: [4 + 2] Cycloaddition of butadiene and ethene

Reaction Scheme

The transition state in the Diels-Alder reaction of butadiene and ethene was simulated via a semi-empirical/PM6 method. The optimised structure was then used to perform an IRC calculation in order to investigate the bond lengths and orbital symmetry requirements of the reaction.

Fig. 1: Butadiene and Ethene reaction scheme.

Theory

Fig. 2: Molecular diagram of the butadiene/ethene transition state.

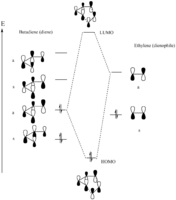
(Fv611 (talk) 16:17, 5 April 2017 (BST) The MOs you have drawn are correct but you are missing the S/S FO combination. You know that there are 4 TS MOs, so why only draw half of them? Additionally, you label them as HOMO and LUMO, when they actually correspond to HOMO-1 and LUMO+1.)

We would expect this reaction to undergo in a synchronous fashion with the butadiene being the electron rich species, where a normal electron demand [4+2] cycloaddition takes place. For a successful reaction to occur, the symmetry of the HOMO in butadiene should align with the LUMO in ethene in order to fulfil the Woodward-Hoffmann rule, resulting in a non-zero orbital overlap in the transition state. The general rule is stated as follows:

symmetric + symmetric = non-zero overlap
asymmetric + asymmetric = non-zero overlap
symmetric + asymmetric = zero overlap

Note that the energy difference between the HOMO and LUMO in ethene is expected to be larger than in butadiene, as an increase of π electrons in a delocalised system would decrease the energy gap according to Hückel Theory.

Simulation Outcome

Orbital Analysis

Semi-empirical/PM6 optimisations were performed for both of the starting materials, and the HOMO and LUMO of each are shown in Table 1.

Table 1. MOs throughout the reaction coordinate.

Ethene MOs	Butadiene MOs	TS MOs

From the table above, we can confirm that the HOMO of butadiene couples with the LUMO of ethene to form the HOMO and LUMO + 1 orbitals of the transition state, whereas the LUMO of butadiene and HOMO of ethene give rise to the HOMO - 1 and LUMO of the transition state. If we look at the corresponding molecular orbitals in detail, we can conclude that only orbitals with the same symmetry would interact, yielding the formation of two new C-C σ bonds seen in the cyclohexene product. The simulation outcome confirms with theory, suggesting that reactions are forbidden when orbital symmetries do not align.

(Fv611 (talk) 16:17, 5 April 2017 (BST) You say that butadiene HOMO (AS) and ethene LUMO (AS) combine to form HOMO (S) and LUMO+1(AS). This is incorrect, as an AS/AS combination will yield two AS MOs. In the same way the butadiene LUMO (S) and the ethene HOMO(S) will yield the TS HOMO (S) and LUMO (S) but not the HOMO-1(AS).)

Bonds Analysis

Comparing the original starting materal bond lengths to the simulated transition state, it is evident that the C-C σ bonds are generally shortened and the C=C π bonds are lengthened, resembling both the formation and breaking of C=C π bonds. These bonds were shown to be around 1.38 Å, which is in the range of the typical sp3 C-C σ bond length (1.54 Å) and the sp2 C=C π bond (1.34 Å), suggesting a partial double bond character. It is also worth noting that the distances between C2 - C3 and C6 - C1 in the transition state were lying between the typical C-C σ bond length and the combined covalent radii of carbon (3.4 Å), which is responsible for the new bond formation between the two merging molecules. The exact distances between the bonded carbon atoms can be found in Table 2.

Table 2. Inter-carbon distances throughout the reaction profile.

	Bond Length / Å
	C1-C2	C2-C3	C3-C4	C4-C5	C5-C6	C6-C1
Starting Material	1.32737	N/A	1.33539	1.46833	1.33539	N/A
Transition State	1.38170	2.11466	1.37974	1.41107	1.37972	2.11509
Product	1.54091	1.54040	1.50090	1.33784	1.50090	1.54040

Reaction Coordinate

Fig. 3: Vibration of reaction path.

The frequency optimisation of the transition state structure showed a vibration at -948.16 cm-1, which depicts an imaginary frequency. This vibrational mode corresponds to the reaction pathway between the starting material and the product, which shows the molecules going towards and away from each other in a synchronous manner, suggesting the two new bonds form in a concerted fashion.

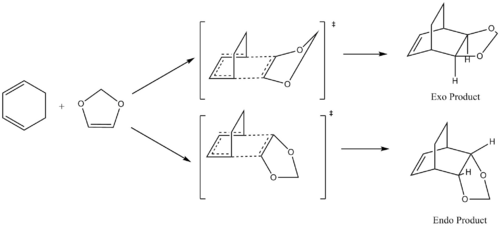
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction Scheme

The following reaction is similar to the reaction of butadiene and ethene, only with the slight difference that there are now substituents attached to the double bonds. The presence of these substituents creates two possible product, exo and endo. From the simulation, we were able to calculate the corresponding energies and determined the kinetic and thermodynamic product of the reaction.

Fig. 4: Cyclohexadiene and 1,3-Dioxole reaction scheme.

Orbital Analysis

Fig. 5: Cyclohexadiene and 1,3-Dioxole reaction molecular orbital diagram.

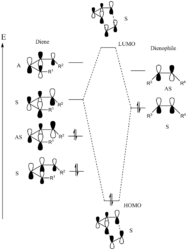
The B3LYP/6-31G(d) method was used in this exercise to aid a more accurate simulation. Semi-empirical/PM6 method was first used to generate initial structures, as this is quicker than running all simulations with the B3LYP/6-31G(d) method. The outcome of the simulation suggested an inverse electron-demand Diels-Alder mechanism for this reaction, and the orbitals involved are shown both in the molecular diagram in Figure 4 and in Table 3 and 4.

(In your table below you show 4 orbitals in each of the TSs. This isn't reflected in your MO diagram in figure 5. There are an additional 2 MOs that results from the combination of the antisymmetric cyclohexadiene HOMO and dioxole LUMO. Tam10 (talk) 11:03, 5 April 2017 (BST))

Exo

In the reaction pathway that leads to the exo product, the HOMO of 1,3-Dioxole linearly combined with the LUMO of cyclohexadiene. From the simulated transition state, the two oxygens in the dioxole ring was shown to be away from the partially formed double bond. However, the methyl group in between the two oxygens shows a potential steric clash with the two sp3 carbons in the cyclohexadiene ring, which might affect the stability of both the transition state and the final product.

Table 3. MOs of the Exo reaction.

1,3-Dioxole MOs	Cyclohexadiene MOs	TS MOs

Endo

In contrast, the transition state shown in Table 4 indicates that the lone pair on the two oxygens form favourable π-interactions with the new forming double bond. From these secondary orbital interactions, we would expect the activation energy in forming the endo product would be lower than the exo product. The steric clash observed in the exo transition state does not appear in here, as the methyl group in the dioxole is now directly under two carbons with partial sp2 character, meaning the clashing hydrogens would be further away compared to the exo case.

Table 4. MOs of the Endo reaction.

1,3-Dioxole MOs	Cyclohexadiene MOs	TS MOs

Energy Calculations

After running IRC calculations, the Gibbs free energy of reaction and the activation energy was extracted for both the endo and exo pathways, and the results are shown in Table 5.

Table 5. Energies along the reaction path.

	Energy / kJ mol-1
	S.M.	T.S.	Product	EA	ΔGr
Endo	-1313798.018	-1313638.011	-1313862.745	160.0071622	-64.72748504
Exo	-1313798.018	-1313630.302	-1313859.259	167.7154406	-61.24090679

From the simulated results, the endo pathway was shown to require a lower activation energy as well as giving the more energetically stable product, meaning the endo product is both kinetically and thermodynamically favoured. This can be explained by the secondary orbital interactions between the lone pair on oxygen and the π system in the 6-membered ring, which appears in both the transition state and the final product.

Nf710 (talk) 20:44, 16 April 2017 (BST) Your energyies are correct/ good conculsions maade and good arguements backing them up. it would have been good if you could have included diagrams to back up your arguments.

Exercise 3: O-Xylylene-SO2 Cycloaddition

Reaction Scheme

Fig. 6: o-Xylylene-SO2 Cycloaddition reaction scheme.

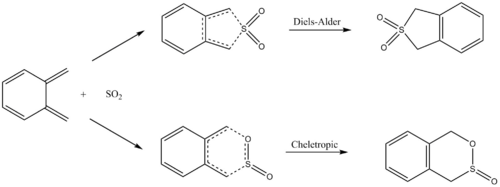
Reaction Coordinate

After running the IRC simulation, the reaction pathway was recorded as an animation and is shown in Table 6. From this, we can observe that as the reaction coordinate reaches the transition state, aromaticity forms within the xylylene ring, which provides stabilisation to the molecule. Due to the instability of xylylene itself, the formation of the aromatic ring becomes the driving force of the reaction.

Table 6. Reaction pathways of the exo, endo and cheletropic product.

	Animated IRC
Endo
Exo
Cheletropic

Energy Calculations

Fig. 7: Reaction profile of the o-Xylylene-SO2 cycloaddition.

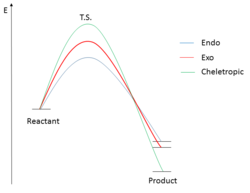
From Table 7, we can confirm that the endo transition state has the lowest energy barrier of activation, giving the kinetic product; whereas the cheletropic reaction has the lowest Gibbs free energy of reaction, hence giving the thermodynamic product of the reaction. An energy profile in Figure 7 can be found in describing the different pathways of this reaction.

Table 7. Relative energies of the three different reaction pathways.

	Energy / kJ mol-1
	S.M.	T.S.	Product	EA	ΔGr
Endo	154.422861	237.7594324	56.98507596	83.33657136	-97.43778504
Exo	154.422861	241.7579705	56.32871711	87.33510951	-98.0941439
Cheletropic	154.422861	260.0782589	-0.005250871	105.6553979	-154.4281119

(Don't use fictitious curved lines in energy profiles. Straight and dotted lines are easier to draw and read. They also give no information about gradients and curvature when there isn't any Tam10 (talk) 11:03, 5 April 2017 (BST))

Conclusion

The semi-empirical/PM6 and B3LYP/6-31G(d) methods were used to run transition state simulations in GaussView5.0, where bond energies and transition state orbital interactions of three cycloaddition reactions were investigated. These calculations provides information about the reaction such as the electron demand mechanism, reaction and bond energies, and the visualisation of different molecular orbital involved in the reaction.

Reference

<references>