Rep:MOD:spk15TS
Introduction
What is a potential energy surface?
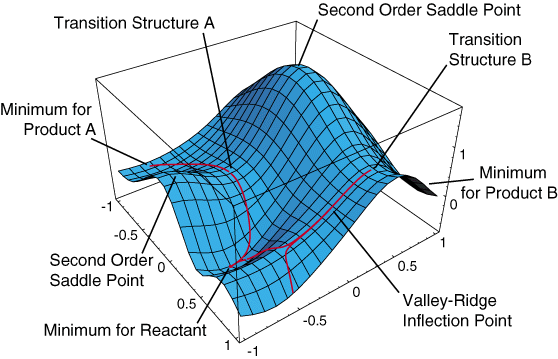
The potential energy surface (PES) describes how the energy of a system in a particular state changes with the structure of the molecule. A simple representation of the potential energy surface is shown in Figure 1, in which the potential energy of the system is given by the vertical coordinates and two geometric variables are given by the horizontal coordinates. Although most molecules have more than two geometric variables, most of the key features of a PES can be represented in such a landscape.
What are a minimum and transition state?
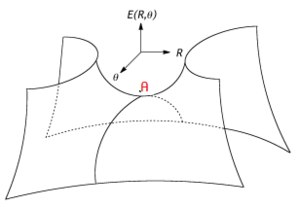
A minimum in the potential energy surface represents the equilibrium structure of the reactants, products or intermediates. The lowest energy pathway between the reactant minimum and the product minimum is the reaction path. The highest point on the lowest energy reaction path is the transition state (TS) for the reaction. A TS is a maximum in one direction (the direction connecting reactant and product along the reaction path) but is a minimum in all other directions perpendicular to the reaction path, making it first-order saddle point. The potential energy surface around a transition state is shown more clearly in Figure 2, where the point A is a maximum along the θ direction but a minimum in the R direction.2
How do energy derivatives vary between minimum and transition states?
The first and second derivatives of the energy (E) with respect to geometrical parameters (x) can be used to confirm the character of minima and TSs. The matrix of the first derivative is given by the gradient of the PES. Both a minimum and TS are characterised by having a zero gradient on the PES. Since the negative of the gradient is the vector of forces on the atoms in the molecule, the minimum and TSs both have zero forces acting on them and are also termed stationary points.
What distinguishes a minimum and a transition state is the curvature of the potential energy surface around the stationary point which is given by the force constant (second derivative) matrix.The matrix of second derivatives of the energy is known as the Hessian. The eigenvectors of the Hessian correspond to the normal modes of vibration (plus 5 or 6 modes for translation and rotation). For a structure to be classified as a minimum, the gradient must be zero and all the eigenvalues of the Hessian must be positive. Using the model for a diatomic molecule, the vibrational freqency is given by
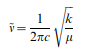
Therefore, if the Hessian matrix and subsequently second derivative of E is positive, the vibrational frequencies must all be positive at a minimum. For a TS, the PES is a maximum along the reaction path and a minimum in all other perpendicular directions. Therefore, a TS is characterised by a negative second derivative of E with respect to x in one dimension, and thus one negative Hessian eigenvalue. Since the minimum has a positive second derivative along all dimensions, the curvature at a minimum is positive. The transition state is the maximum point along the reaction path and therefore has negative curvature along the reaction path.3
Nf710 (talk) 21:59, 8 February 2018 (UTC) This is the best explaination about hessians that I have seen. well done. You could have talk a bit about the quantum chemical methods.
Exercise 1: Reaction of Butadiene with Ethylene
Reaction Scheme
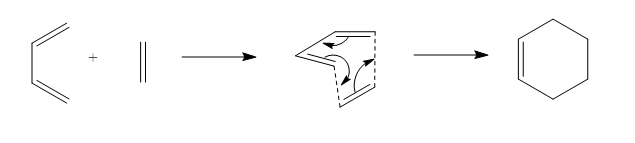
Butadiene reacts with Ethylene in a concerted, suprafacial [4+2] cycloaddition according to the mechanism shown in Figure 3.
Trans-butadiene
For this [4=2] cycloaddition, butadiene has to be in a cis conformation. However, butadiene usually exists as a more stable trans-isomer. (96% of the time butadiene is in the trans conformation).4 The reaction energy for the conversion from trans to cis-butadiene is +4.16 kj/mol-1 at the PM6 level.
| Trans-butadiene | ||
|---|---|---|
MO Analysis of reaction
| Butadiene | Ethylene | TS | Product | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Butadiene | MO diagram for the formation of the Butadiene/Ethylene transition state | Ethylene | ||||
|---|---|---|---|---|---|---|
 |
||||||
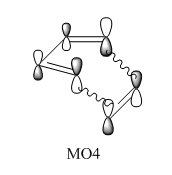
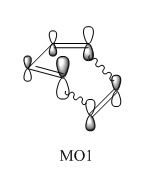
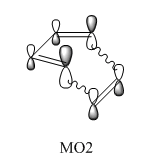
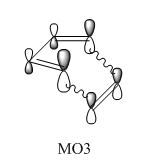
In this normal electron demand [4+2] Diels-Alder reaction, the diene (butadiene) is more electron rich than the dienophile (ethylene) since it has more pi electrons due to one more double bond. Hence, butadiene has orbitals that are higher in energy than the orbitals of ethylene. The major interaction is between the antisymmetric LUMO of ethylene and HOMO of butadiene since they are closest in energy. The bonding interaction between these two frontier molecular orbitals produces MO1. The transition state HOMO, MO2 is the bonding interaction between the symmetric LUMO of butadiene and HOMO of ethylene. MO3 is the antibonding pair of MO2, formed from the antibonding interaction between the LUMO of butadiene and HOMO of ethylene. It is only slightly higher in energy than the LUMO of butadiene, indicating it is only destabilised by a small amount. Finally, MO4 is formed by the bonding interaction between the asymmetric highest energy frontier orbital of butadiene and the asymmetric LUMO of ethylene. Due to the close energy of all the frontier molecular orbitals, there is some orbital mixing between the orbital formed by the HOMO of butadiene and LUMO of ethylene and this high energy butadiene orbital.5
(Fv611 (talk) A lot of confusion here. The symmetry labels of the TS MOs are missing. Additionally, even though you seem to understand the bonding/antibonding pair that forms MO2/MO3, for some reason you postulate that the MO4/MO1 pair can result from the combination of 3 fragment molecular orbitals. Furthermore, you know from your calculations that the TS LUMO is lower in energy than the butadiene LUMO, and yet you draw them on the same level. Finally, you are not showing the ethylene HOMO jmol. Overall, this section would have benefited from more attention.)
 |
 |
 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Woodward-Hoffmann Rules and Orbital Symmetry
A reaction is 'allowed' thermally when the total number of [4q+2]s + [4r]a components is odd. In this reaction, the orbitals interact with orbitals of the same symmetry (symmetric with symmetric or asymmetric with asymmetric) so all the components are suprafacial since the new bonds form on the same face at both ends of the component.

Bond length analysis of the reaction

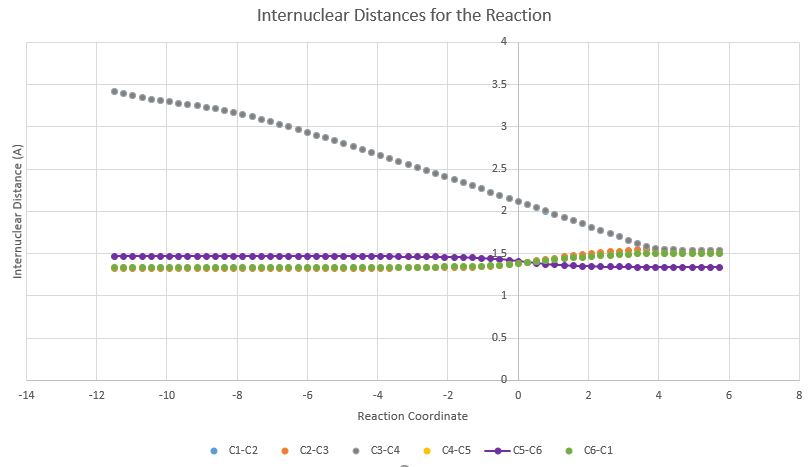
As the reaction proceeds, the carbon centres change from sp3 to sp2 hybridised or vice versa. The carbon-numbering is shown in Figure 4.
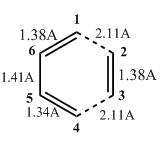
The largest change in bond length is between C1-C2 and C3-C4 where the new sigma bonds are formed. The bond lengths decrease from 3.41A (too far for any bonding interaction so implies different molecules) to 1.54A, which is typical of a sp3-sp3 single bond. At the same time, the C5-C6 bond length decreases from 1.47A(sp2-sp2) to 1.34A (which is the typical bond length of a C=C). The C1-C6 and C4-C5 double bonds increase in length from 1.34A to 1.50A. 1.50A is exactly the typical sp3-sp2 bond length and shows the change from a double to single bond. In the TS, the partly formed C-C bonds have a bond length of 2.11A, which is in between the combined VDW radius of the 2 C atoms (1.70A x 2 = 3.40A) and the typical sp3-sp3 single bond length (1.54A).
Vibration corresponding to the reaction path at the transition state
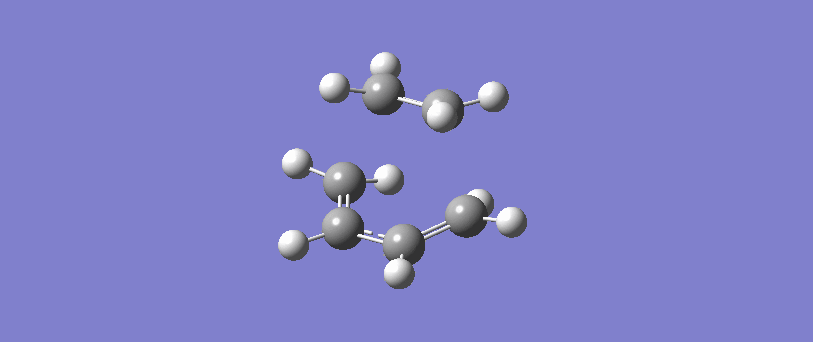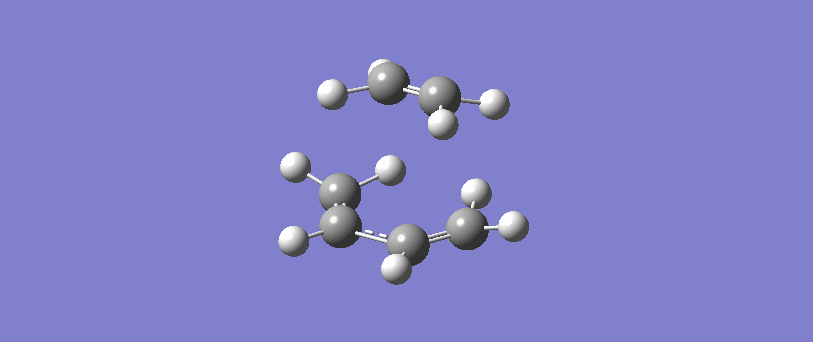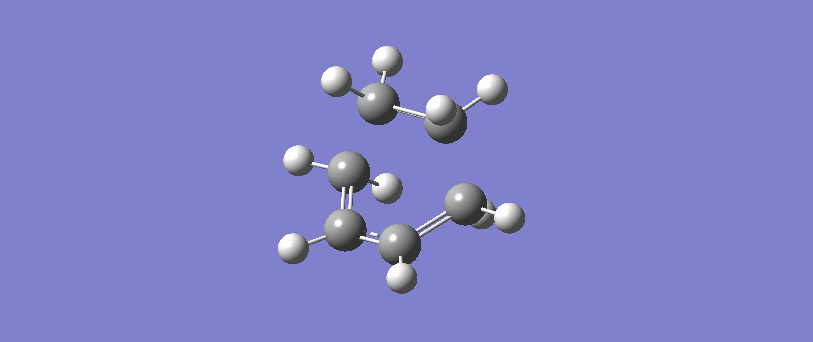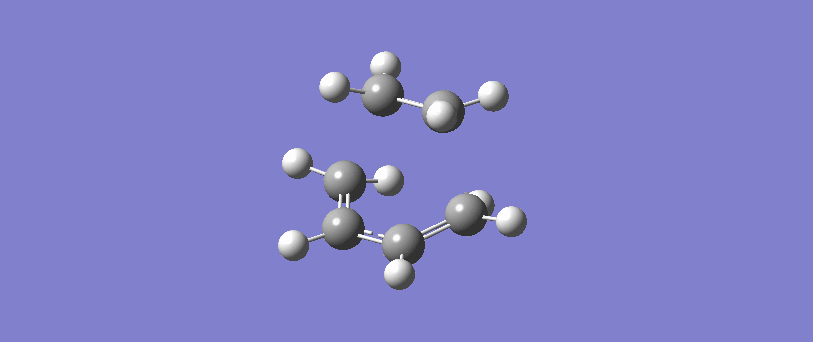
The formation of the two bonds is synchronous. The movement of the bonds at the transition state show that C2 approaches C1 at the same time as C3 approaches C4, and the two sigma bonds form simultaneously. This implies that the bonds form at the same time, and possibly but not necessarily at the same rate.
Link to Exercise 2
https://wiki.ch.ic.ac.uk/wiki/index.php?title=MOD:spk15TSEx2
Link to Exercise 3
https://wiki.ch.ic.ac.uk/wiki/index.php?title=MOD:spk15TSEx3
Conclusion
The focus of this computational lab was on locating transition structures for a series of reactions and abstracting information about the reaction.Two electronic structure methods were employed: the semi-empirical method PM6 and the Density Functional Theory (DFT) method B3LYP to optimise the structures while IRCs were run on the transition state to confirm they connected the reactants and products along the lowest energy pathway. The symmetry requirements according to the Woodward-Hoffmann Rules for cycloadditions were explored along with the 2 types of Diels-Alder reaction- normal electron demand and inverse electron demand. The relative energy levels of the frontier molecular orbitals were examined and the HOMO of the dienophile was found to be higher than that of diene in an inverse electron demand reaction while the opposite was true for a normal electron demand reaction. However, this was found not to affect the relative energy levels of the transition state. The thermochemistry of the reactions was also studied and it was found that secondary orbital interactions could lower the energy of transition states, making a product more kinetically favourable. In a reversible reaction, steric hindrance can also determine the relative thermodynamic stability of a product.
References
1. Potential Energy Surface - Chemistry LibreTexts.
2. Schlegel, H. B. (2011). Geometry optimization, 1(October), 790–809.
3. Ot, W. J. (1990). Computational quantum chemistry. Journal of Molecular Structure: THEOCHEM (Vol. 207).
4. Butadiene: A Molecular Mechanics Study.
5. Fleming, Ian (1978). Frontier Orbitals and Organic Chemical Reactions.
6. Progress in Heterocyclic Chemistry, Volume 28, 1st Edition.
7. Ho, G. M., Huang, C. J., Li, E. Y. T., Hsu, S. K., Wu, T., Zulueta, M. M. L., … Hung, S. C. (2016). Unconventional exo selectivity in thermal normal-electron-demand Diels-Alder reactions. Scientific Reports, 6(October), 1–10.
8. Secondary orbital interactions determining regioselectivity in the Diels-Alder reaction.
Peter V. Alston, Raphael M. Ottenbrite, and Theodore Cohen, The Journal of Organic Chemistry 1978 43 (10), 1864-1867
9. Wiley, 1985. Advanced Organic Chemistry: Reactions, Mechanisms, and Structure.
10. Aromaticity and the Hückel 4n + 2 Rule - Chemistry LibreTexts.