Transition Structures

Introduction

Diels-Alder Reactions

In the course of this investigation, the transition states of several Diels-Alder reactions are explored.

Diels-Alder reactions are 4+2 cycloadditions between a diene and a dienophile.

Some Diels-Alder reactions can result in either endo or exo products, depending on the trajectory of approach of the dienophile. These alternative paths have different reaction energies and barriers.

Normal Diels-Alder reactions involve the interaction of the HOMO of the diene and the LUMO of the dienophile, as shown in Figure 1. However, as Figure 1 also shows, there is an inverse-demand Diels-Alder, in which the LUMO of the diene and the HOMO of the dienophile interact. This tends to happen when there are electron-donating groups on the dienophile, increasing the energy, and electron-withdrawing groups on the diene, decreasing the energy.

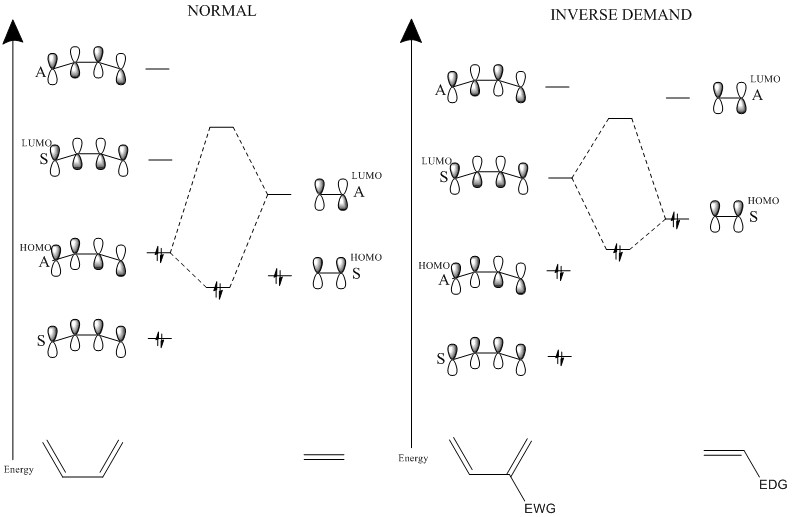
Figure 1: An MO Diagram showing Normal and Inverse Demand Diels Alder Reactions

Both normal and inverse-demand Diels-Alder reactions will be looked at.

Potential Energy Surfaces

Potential energy surfaces (PES) are quantum mechanical conceptual tools that relate the potential energy of a system with its geometry. The degrees of freedom dictate the dimensions of the potential energy surface. PESs rely upon the Born-Oppenheimer approximation which allows for the separation of the nuclear degrees of freedom and the electronic degrees of freedom by stating that the nuclei are fixed in motion relative to the electrons.

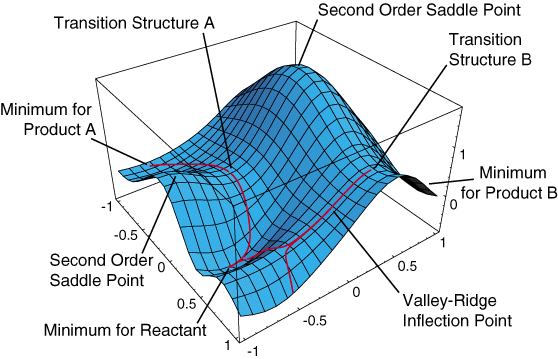
Figure 2: A PES showing Relevant Features^[1]

The minima relate to chemically stable configurations. Conversely, the maxima relate to chemically unstable configurations.

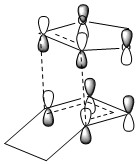
As shown in Figure 2, transition states are first order saddle points on the potential energy surface. The transition state, as a saddle point, is a minimum between two maxima (second order saddle points) and a maximum between the two minima of the reactants and products. The geometry at the transition state will result in an imaginary frequency, appearing as a negative number, due to the square root of a negative force constant in the harmonic oscillator.

Figure 2 also shows the concept of alternative pathways, transition state A and transition state B could correspond to the endo and exo pathways discussed above.

Nf710 (talk) 23:49, 30 November 2017 (UTC) You need to explain this with respect to the dericatives

Computational Methods

The two methods used are the semi-empirical PM6 method and the DFT-hybrid B3LYP method which uses a 6-31G(d) basis set.

The simplest ab initio method (when the energies are derived from first principles) is based on the Hartree-Fock (HF) method, in which the wavefunction of the system is expressed through the use of a linear combination of Slater determinants with fixed coefficients. The Hartree-Fock method neglects to account for electron correlation and hence is discouraged for large systems.

Nf710 (talk) 23:50, 30 November 2017 (UTC) Good! slater determinants allow for the electrons to be experessed with the correct fermionic anti symetry

The PM6 method is based on the same MO theory as the HF ab initio method but it also incorporates empirical data as approximations for certain integrals. This allows fewer calculations to be made and results in a less computationally expensive method. However, these approximations mean the accuracy of this optimisation is compromised.

The B3LYP method is a DFT-hybrid method. DFT methods are based on electron density, an observable physical property, as opposed to wavefunctions. The DFT-hybrid method incorporates both the HF method, which can find the exact exchange energy when ignoring correlation effects, with the DFT method, which does include the electron correlation effects. DFT-hybrid methods are much more accurate than non-hybrid DFT methods at the cost of computational power. In comparison to the PM6 method, fewer approximations are used in the B3LYP method resulting in a more accurate optimisation but it is more computationally expensive.^[2]

For exercises 1 and 3, the PM6 level was used, while exercise 2 used the B3LYP method.

Nf710 (talk) 23:52, 30 November 2017 (UTC) This is correct b3LYP is a hybrid because it calculates the bulk of the hamiltonian with a DFT hamiltonian. But the exchange correlation part is treated with a further harteee fock calculation.

Finding the Transition State

Three methods were used to find the transition state. The first method is the fastest and involves estimating the transition state and optimising it immediately. The second method is also fast but more reliable: this involves estimating the transition state, freezing the atoms involved in bond formations and optimising the structure to a minimum before optimising the transition state. The third method is the most reliable as it involves the least amount of guesswork but requires additional steps and hence the most computational effort. The third method involves optimising the reactants or the products and finding the transition state by changing bond lengths.

For exercise 1, method 2 was used due to the relative simplicity of the reactants, allowing the transition state to be guessed easily.

For exercises 2 and 3, method 3 was the most successful as the transition state was more complex.

Exercise 1ː Diels Alder with Butadiene and Ethene

In this exercise, the transition state of a π4s + π2s cycloaddition using the reactants butadiene and ethene is explored. The reactants, butadiene and ethene, and the transition state were optimised at the PM6 level. The transition state was confirmed with a frequency calculation and an IRC. The products were optimised at the PM6 level. Figure 3 shows the reaction scheme.

Figure 3: Reaction Scheme showing the formation of Cyclohexene through a 4+2 cycloaddition reaction

MO Diagram

Figure 4 shows the MO diagram for the formation of the butadiene/ethene transition state, including basic symmetry labels. This is a normal Diels-Alder reaction, in which the HOMO of the diene reacts with the LUMO of the dienophile.

(Fv611 (talk) Your MO pairings are correct, but your energy levels are not. As you haven't included log files or JMOls, I don't know if this is because your optimisations weren't done correctly or if it is because you haven't adjusted your MO diagram based on the MO energies you've calculated. For example, all the reactant HOMOs should be lower in energy than the TS HOMO-1.)

These are shown by the MOs of the optimised reactants below.

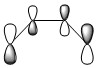Table 1: A Table showing the corresponding MOs to the HOMO and LUMO of both butadiene and ethene
Butadiene HOMO Asymmetric		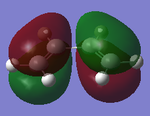Butadiene LUMO Symmetric
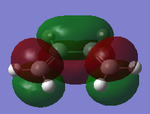
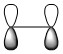Ethene HOMO Symmetric		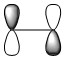Ethene LUMO Asymmetric

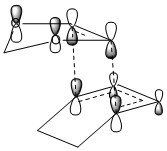
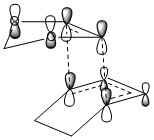
The four MOs that the reactant MOs produce for the transition state are shown in Table 2 along with their corresponding MOs from the transition state after optimisation - these are the HOMO-1, HOMO, LUMO and LUMO+1.

Table 2: A Table showing the MOs produced for the Transition State
LUMO+1 Asymmetric
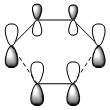LUMO Symmetric
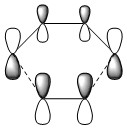HOMO Asymmetric
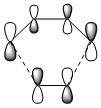HOMO-1 Symmetric

As shown, the symmetry of the combining orbitals must be the same. This is because the orbital overlap integral is zero for symmetric-antisymmetric interactions and is non-zero for symmetric-symmetric and antisymmetric-antisymmetric interactions. Hence, symmetric-antisymmetric combinations are 'forbidden' and only same-symmetry combinations are 'allowed' as an orbital overlap is necessary for interaction.

Bond Lengths

The measurements of the C-C bond lengths of the reactants, products and transition state are shown below.

Figure 5: A Labelled Diagram of the Reactants

Table 3: A Table showing the Bond Lengths between Carbons for the Reactants, Transition State and Product
Carbon-Carbon Bond	Reactants (Å)	Transition State (Å)	Product (Å)
C₁ to C₂	1.34	1.38	1.50
C₂ to C₃	1.47	1.41	1.34
C₃ to C₄	1.34	1.38	1.50
C₄ to C₅		2.11	1.54
C₅ to C₆	1.33	1.38	1.53
C₆ to C₁		2.11	1.54

The van der Waals radius of carbon is 1.7 Å, the bond length of an sp² hybridised carbon is 1.3 Å and the bond length of an sp³ hybridised carbon is 1.5 Å.

From the data in the table, the changes of bond length as the reaction proceeds can be seen. The double bonds in the diene (C₁ to C₂ and C₃ to C₄) are shown to elongate throughout the process as they become single bonds, while the single bond in the diene (C₂ to C₃) decreases in length as it becomes a double bond. Similarly, the double bond in the dienophile increases in bond length as it becomes a single bond.

For interaction to occur between two carbon atoms, they must be closer than two van der Waals radii - 3.4 Å. In the transition state, the bond lengths between C₄ to C₅ and C₆ to C₁ show a length of 2.11 Å. This is within double the van der Waals radius for carbon and hence the two atoms can be said to be interacting.

(Fv611 (talk) How does the length of the bond being formed compare with a typical sp3-sp3 bond length? What can you deduce from that?)

In the product, all carbon-carbon bonds are around 1.5 Å, the typical bond length of a carbon-carbon single bond, with the exception of C₂ to C₃, which is also a typical length for a carbon-carbon double bond.

Imaginary Frequencies

As mentioned in the introduction, transition states are characterized by a single imaginary frequency as a result of the square root of the negative force constant. This appears as a negative frequency in GaussView. Figure 6 shows an animation of this.

From the animation, it can be seen that the formation of the two new bonds is synchronous.

Exercise 2ː Cyclohexadiene and 1,3-Dioxole

Exercise 2 explores another 4+2 cycloaddition involving the reactants cyclohexadiene and dioxole. In this case, there are two possible products depending on the trajectory of approach to the transition state. The possible products are the endo product and the exo product. Figure 7 shows the reaction scheme including both products and transition states.

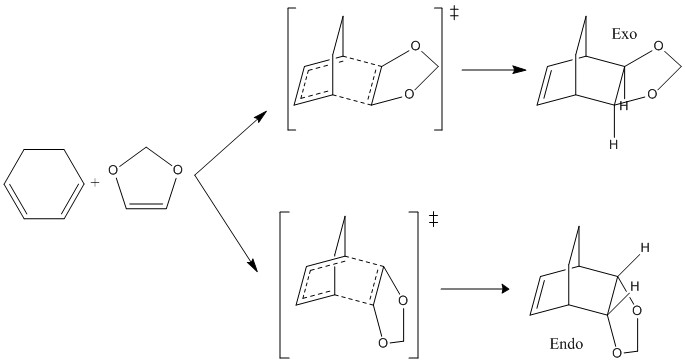
Figure 7: Reaction Scheme showing Exo and Endo Products of a Cycloaddition invovling Cyclohexadiene and a 1,3-dioxole

The endo and exo transition states were located using method 3. They were optimised to the B3LYP/6-31G(d) level. Frequency calculations and an IRC were taken for both, confirming the transition state.The endo and exo products as well as the reactants were also optimised to the B3LYP/6-31G(d) level.

MO Diagram

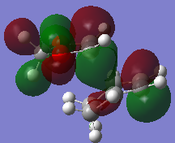
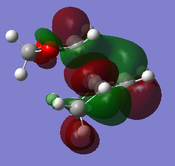
Using the information from the PM6 optimisation, the MO diagram from exercise 1 was adjusted to apply to this reaction. The addition of the oxygen atoms results in a higher energy dienophile, resulting in an inverse demand Diels-Alder reaction. This is shown in Figure 8.

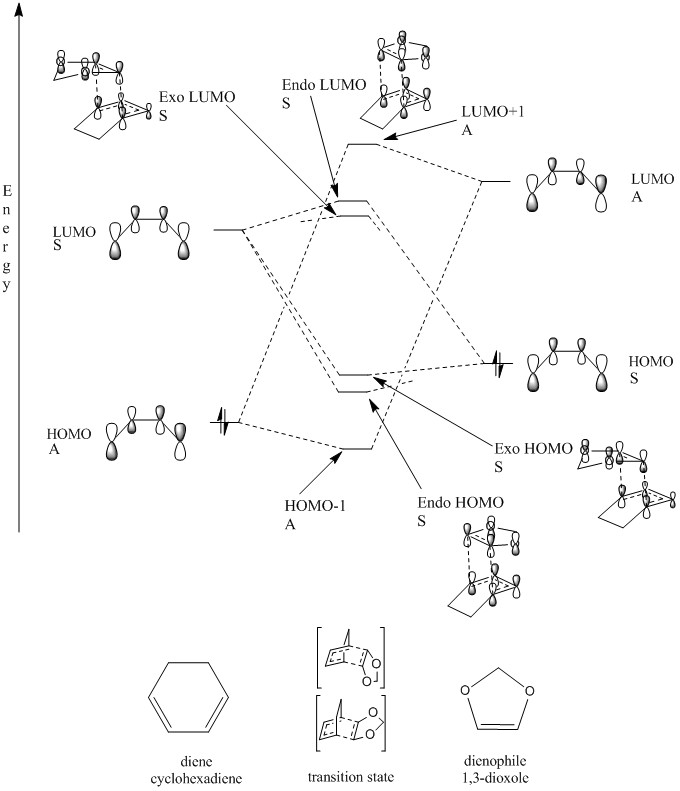
(Fv611 (talk) Good MO diagram, and well done on reporting the difference between the exo and the endo case. However the TS MO's are not placed according to their relative energies, as both bonding TS MOs are higher in energy than the diene's HOMO, and both antibonding TS MOs are lower in energy than the dienophile's LUMO.)

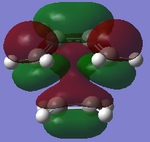
The corresponding MOs from the optimised transition states are shown below.

Table 4: A Table showing the corresponding MOs to the HOMO and LUMO of both the Exo and Endo Transition States
Exo Transition State HOMO Symmetric		Exo Transition State LUMO Symmetric
Endo Transition State HOMO Symmetric		Endo Transition State LUMO Symmetric

Secondary Orbital Interactions

The 'endo rule' is generally applicable to irreversible Diels-Alder reactions. The endo product is more favoured due to the presence of secondary orbital interactions. The p orbitals of the oxygen atoms can interact with the pi system of the diene resulting in favourable bonding interactions for the endo transition state and product. This is shown in the HOMO of the endo transition state above.^[3]

This favourable bonding interaction means the reaction barrier for the endo transition state will be lower than that of the exo.

Thermochemistry

The table below shows the energies of the reactants, products and transition states in Hartrees and kJ/mol.

Table 5: A Table showing the Energies of the Reactants, Products and Transition States
Compound	Energy (Hartrees)	Energy (kJ mol^-1)
Cyclohexadiene	-233.321033	-701187.4340
1,3-Dioxole	-267.068132	-612584.4188
Reactants	-500.389165	-1313771.8528
Endo Transition State	-500.332152	-1313622.1651
Exo Transition State	-500.329168	-1313614.3307
Endo Product	-500.418691	-1313849.3733
Exo Product	-500.417322	-1313845.7790

From this, the reaction barriers and reaction energies are tabulated at room temperature, shown in Table 6.

Table 6: Showing the Energies of the Reactants, Products and Transition States
Product Conformation	Reaction Barrier(kJ mol^-1)	Reaction Energy (kJ mol^-1)
Endo	149.688	-77.521
Exo	157.522	-73.962

As the reaction barrier is smaller for the endo transition state, it is the kinetically favourable pathway. The reaction energy is also lower for the endo product, hence it is the thermodynamically favourable product as well.

Nf710 (talk) 23:56, 30 November 2017 (UTC) Your energies are correct in this section. But the discussion is extremly brief. your Mos are nice. but maybe you could have developed your ideas abit more about SOO and the electron demand of the reaction.

Exercise 3ː Diels Alder vs Cheletopic

In this exercise, three different transition states were investigated. Two of these were the endo and exo transition states and products of a Diels Alder reaction. The third was a cheletropic reaction. Figure 9 shows the reaction scheme for all three.

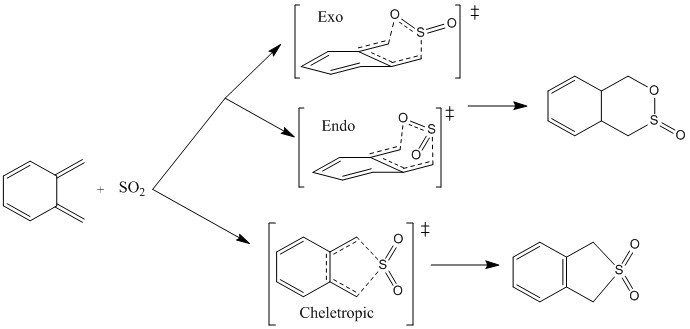
Figure 9: Reaction Scheme showing the transition states for the exo product, the endo product and the cheletropic product

These were optimised to the PM6 level. The transition states were confirmed using IRCs and frequency calculations.

IRC

Figures 10-12 show the visualisation of the reaction coordinates for all three paths.

The formation of the endo and exo products can be seen to be asynchronous as the C-O bond is formed before the S-O bond.

The lack of stability of xylylene can be explained through the visualisation of the IRCs. As the xylylene reacts, the bond lengths of the six-membered ring equalize as it becomes aromatic. This is a much more stable configuration. Hence, xylylene would prefer to react to form an aromatic ring instead of two diene sites.

Thermochemistry

Table 7: A Table showing the Energies of the Reactants, Products and Transition States
Compound	Energy (Hartrees)	Energy (kJ mol^-1)
SO₂	-0.11861	-311.4211
Xylylene	0.1781	467.6331
Reactants	0.0595	156.2120
Endo Transition State	0.0906	237.7653
Exo Transition State	0.0923	241.7508
Cheletropic Transition State	0.0997	260.0847
Endo Product	0.0216	56.3301
Exo Product	0.0217	56.9865
Cheletropic Product	-0.000002	-0.0053

From this, the reaction energies and barriers can be calculated:

Table 8: Showing the Energies of the Reactants, Products and Transition States
Product Conformation	Reaction Barrier(kJ mol^-1)	Reaction Energy (kJ mol^-1)
Endo	81.55	-99.88
Exo	85.54	-99.23
Cheletropic	103.87	-156.22

From this information, a reaction profile showing all three paths can be configured.

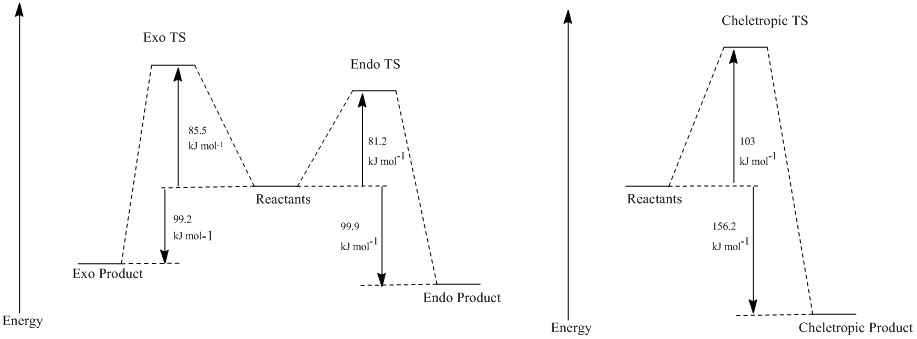
Figure 13: A Reaction Profile showing the Endo, Exo and Cheletropic Pathways

This shows that the kinetic and thermodynamic product is the endo product.

Conclusion

The transition states of multiple Diels-Alder reactions were found using two computational methods, PM6 and B3LYP, depending on the accuracy needed.

The reaction barriers and reaction energies were found through the use of these methods, allowing for comparison of the exo and endo transition states and products. The endo transition state and product were found to be lower in energy than the exo for both exercises 2 and 3. Alternative pathways, such as the cheletropic reaction, were shown to be disfavoured due to the high energy of the transition state and the product.

MO theory was explored in relation to the transition states, offering explanations for the increased stability of the endo product by showing the favourable secondary orbital interactions.