Rep:MOD:lonelyTylenol
Module 3: Transition States and Reactivity
Introduction: The Cope Rearrangment
First discovered in 1940 by Arthur Cope [1], the Cope rearrangement is when a 1,5-diene undergoes a heat driven 3,3-sigmatropic rearrangement forming a more stable or energetically equivalent regioisomer. In the below reaction both reactants and products are isoenergetic so the equilibrium constant for both forward and reverse reactions are the same, however, if the 3 carbon on the reactant had an alkyl group attached to it, the resulting product would be have a substituted alkene and would thus, be more thermodynamically stable, shifting equilibrium to the right.

The rearrangement is known to proceed via either a chair or boat transition state by a concerted mechanism, with the boat transition state believed to have the highest energy[2].

The aim of this computational experiment is to investigate the optimized energy minima of these transition states and how the orbital interactions can affect the energy of transition structures and the pathways of a reaction.
Optimization and Analysis of 1,5 Hexadiene
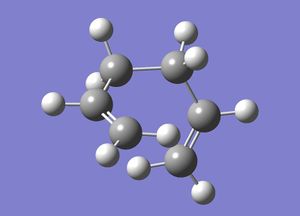
Anti Conformer
1,5-hexadiene with "anti" (anti-periplanar) linkage was drawn in GaussView and then optimised using the Hartree-Fock(HF) 3-21G method. The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the optimization.
Point Group: C2
Total Energy: -231.69260235 a.u.
| File type | .chk |
|---|---|
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | (3-21G) |
| Charge | 0 |
| Spin | Singlet |
| Final Energy | -231.69260235 a.u. |
| Gradient | 0.00001824 a.u. |
| Dipole Moment | 0.2021 Debye |
| Point Group | |
| Calculation Time |
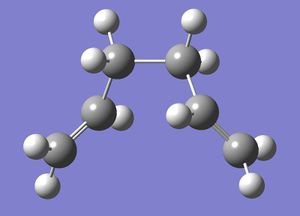
Gauche Conformer
Subsequently,1,5-hexadiene with "gauche" linkage was drawn in GaussView and then optimised using the Hartree-Fock(HF) 3-21G method. The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the optimization.
Point Group: C2
Total Energy: -231.68771613 a.u.
| File type | .chk |
|---|---|
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | (3-21G) |
| Charge | 0 |
| Spin | Singlet |
| Final Energy | -231.68771613 a.u. |
| Gradient | 0.00001461 a.u. |
| Dipole Moment | 0.4550 Debye |
| Point Group | |
| Calculation Time |
The Gauche conformer was found to have a slightly higher total energy than the Anti conformer. This is may be due to the steric clash of the two C=C groups which are nearer to each other in the Gauche conformer, raising the energy of the system.
Lowest Energy Conformer
Although the reason discussed above is a plausible reason why the anti conformer had a lower energy it is not the dominating reason. The core reason why the anti conformer has a lower energy is due to stereoelectronics.
In theory the lowest energy conformer is that where there is a completely anti-periplanar relationship between all the carbon atoms,which leads to orbital stabilisation.
However, after finding the energies of all the confirmations in the table below it was found that a gauche 3 conformer with C1 symmetry was the lowest energy conformer. This is because in this conformation the Van der Waals interacions between H's are at a maximum and the sigma/pi donation in the C=C bonds are at a maximum, there is a stabilising interaction from donation of electron density into the σ* C-H orbital from the π C=C orbital. Furthermore, the Pauli repulsion between neighboring, filled sigma C-H orbitals is restricted in this conformation.
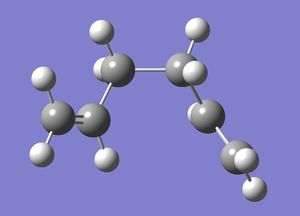
Anti Conformer: Ci Symmetry
Optimization using HF/3-21G method
1,5-hexadiene with "anti" (anti-periplanar) linkage, but with a Ci symmetry, was drawn in GaussView and then optimised using the Hartree-Fock(HF) 3-21G method. The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the optimization.
Point Group: Ci
Total Energy: -231.69253516 a.u.
C-C Bond Length: 1.55 Å (to 3 s.f)
C=C Bond Length: 1.32 Å (to 3 s.f)
The total energy and the shape of the structure is found with the Ci conformer found in the Appendix 1.
| File type | .chk |
|---|---|
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | (3-21G) |
| Charge | 0 |
| Spin | Singlet |
| Final Energy | -231.69253516 a.u. |
| Gradient | 0.00004313 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | |
| Calculation Time |
A thing to note is that due to the symmetry of the molecule the overall dipole moment is 0.
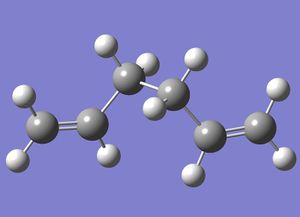
Optimization using B3LYP/6-31G* method
1,5-hexadiene with "anti" (anti-periplanar) linkage, but with a Ci symmetry, was drawn in GaussView and then re-optimised using, the more accurate but longer, B3LYP/6-31G* method. Although, it would be incorrect to compare the total energies of systems analysed using different methods, changing the basis set allows a comparison of bond lengths and point groups.
The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the optimization.
Point Group: Ci
Total Energy: -234.61171032 a.u.
C-C Bond Length: 1.56 Å (to 3 s.f)
C=C Bond Length: 1.34 Å (to 3 s.f)
| File type | .chk |
|---|---|
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | (6-31G(D)) |
| Charge | 0 |
| Spin | Singlet |
| Final Energy | -234.61171032 a.u. |
| Gradient | 0.00003842 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | |
| Calculation Time |
The total energy of the molecule was found to more negative, meaning the resultant structure is more stable, however, the symmetry of the molecule was retained when the more complex basis set was used.
The optimized total energy in literature was found to be -234.32879 a.u.[3] which is slightly more positive.
Frequency Analysis
The purpose of frequency analysis is to find the minimum structure on a potential energy surface (PES). It will also produce the frequencies of vibration in spectra which can then be compared to experimental values, allowing conclusions to be drawn after.
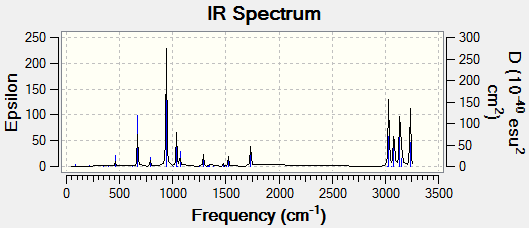
The optimized Ci conformer underwent frequency analysis to confirm the presence of a minimum critical point on it's PES producing positive real values for the vibrational frequencies. The calculation was then run on a HPC server and the D-Space publication of the frequency analysis can be found here.
Low frequencies --- -9.5208 -0.0005 0.0004 0.0007 2.8649 11.0477 Low frequencies --- 74.3242 80.8799 121.4080
The lowest "real" normal mode is found to occur at 74.3242cm-1
Sum of electronic and zero-point Energies= -234.469202 Sum of electronic and thermal Energies= -234.461855 Sum of electronic and thermal Enthalpies= -234.460911 Sum of electronic and thermal Free Energies= -234.500777
| Table Displaying Each Energetic Property and it's respective equation | ||||
| Property | Equation | |||
| Sum of electronic and zero-point Energies | E(0 K) = Eelec + ZPE | |||
| Sum of electronic and thermal Energies | E(298.15 K) = E(0 K) + Evib + Erot + Etrans | |||
| Sum of electronic and thermal Enthalpies | H = E (298.15K) + RT | |||
| Sum of electronic and thermal Free Energies | G = H - TS | |||
Optimization of "Chair" and "Boat" Transition State Structures
Chair Transition State
Hessian Method
Two allyl fragments (CH2CHCH2) were initially. optimized using the HF/3-21G method and placed in an orientation similar to the the chair transition state with a distance of ~2.2Å between both fragments terminal carbons. This was then optimized to a TS using the Berny calculation and the force constants were calculated once.
The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the analysis:
Low frequencies --- -817.9780 -3.5381 -1.0455 0.0002 0.0002 0.0005 Low frequencies --- 1.1751 209.4810 395.9153 ****** 1 imaginary frequencies (negative Signs) ******
An imaginary frequency was found to occur at -817.9780cm-1 which confirms the formation of the correct chair transition state structure.
Sum of electronic and zero-point Energies= -231.466700 Sum of electronic and thermal Energies= -231.461340 Sum of electronic and thermal Enthalpies= -231.460396 Sum of electronic and thermal Free Energies= -231.495206
Terminal forming/breaking bond lengths: 2.02Å (to 3 s.f)
Point Group: C2h
Total Energy: -231.61932242 a.u.
The vibration corresponding to the imaginary frequency at -817.9780cm-1 was also found to be that of the Cope rearrangement.

Frozen Co-ordinated Method
Freezing the reaction co-ordinate and minimizing the rest of the molecule can sometimes generate a more accurate transition state structure, since once the rest of the molecule is fully relaxed after initial optimization, the transition state optimization is started. This means computing the whole Hessian may not be nessecary and just differentiating along the reaction co-ordinate can produce a good approximate. This can save a lot of time in problems where the force constant calculation can take an extensive amount of time.
Two allyl fragments (CH2CHCH2) were initially. optimized using the HF/3-21G method and placed in an orientation similar to the the chair transition state with a distance of ~2.2Å between both fragments terminal carbons. This was then optimized to a TS using the Berny calculation and the force constants were calculated once. The terminal forming/breaking bonds were then frozen whilst the rest of the molecule was optimized, after which the terminal bond lengths were optimized to form a complete chair structure.
The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the analysis:
Terminal forming/breaking bond lengths: 2.02Å (to 3 s.f)
(The bond lengths seem to be the same as those calculated by from the initial guess)
Point Group: C2h
Total Energy: -231.61932243 a.u.
(Note the very slight, probably negligible increase in total energy in comparison to the energy of the guess structure)
Boat Transition State
QST2 Method
Initial, optimization using this method failed as the reactant and product molecules geometries were not close enough to the desired boat transition state and Gaussview simply moved the top allyl fragment without taking into account the possiblity of rotation around the central bonds. As a result a chair like structure was formed:

The D-space publication can also be found here.
The geometries were fixed by adjusting the dihedral and bond angles of the central carbons and the calculation was then run on a HPC server and the D-Space publication of the optimization and analysis can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the analysis:
Low frequencies --- -840.2338 -1.5198 -0.0009 -0.0005 0.0018 4.2777 Low frequencies --- 7.9489 155.3839 382.0904 ****** 1 imaginary frequencies (negative Signs) ******
An imaginary frequency was found to occur at -840.2338cm-1 which confirms the formation of the correct boat transition state structure.
Sum of electronic and zero-point Energies= -231.450930 Sum of electronic and thermal Energies= -231.445302 Sum of electronic and thermal Enthalpies= -231.444358 Sum of electronic and thermal Free Energies= -231.479775
Terminal forming/breaking bond lengths: 2.14Å (to 3 s.f)
Point Group: C2v
Total Energy: -231.60280222 a.u.
The vibration corresponding to the imaginary frequency at -840.2338cm-1 was also found to be that of the Cope rearrangement via the Boat transition state rather than the previous chair transition state.

It is possible that the 1,5 hexadiene conformer which connects the Boat TS is the gauche C2 conformer.
Intrinsic Reaction Co-ordinate (IRC)
The IRC can be considered as the minimum energy pathway going from a reactions transition structure to the structure of it's reactants or products in mass-weighted cartesian on a PES. This allows the possibility to identify the conformer related to a specific transition structure. This is done by taking small steps towards the area of the PES where the gradient is at it's steepest.
In the following analysis, the direction of the IRC was chosen as the forward reactions due to the fact that this reaction is symmetrical. The optimized chair TS was used and the force constants for 50 points were all calculated.
The calculation was then run on a HPC server and the D-Space publication of the analysis can be found here.
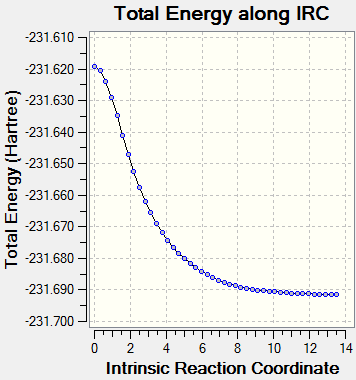
The lowest Total Energy: -231.69157858 a.u. (At the point where the bond has fully formed and the C=C groups are furtherest apart)
The IRC did not actually manage to reach a minimum geometry using only 50 points so the calculation was rerun with 100 points being computed along the reaction co-ordinate. The lowest energy resultant structure was optimized and then analysed and found to resemble the Gauche 2 (C2) conformer from Appendix 1. Furthermore, the lowest energy structure from the IRC was similar to the total energy of the Gauche 2 structure in literature[4].

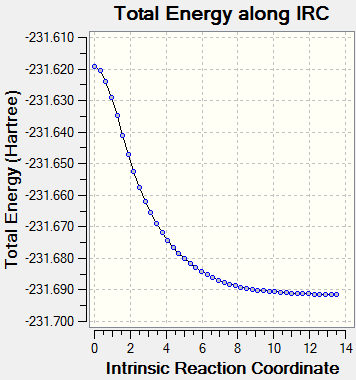
The lowest Total Energy: -231.69157859 a.u.
Activation Energies
In order to calculate the activation energies for the Cope rearrangement of 1,5 hexadiene via both chair and boat transition structures, the structures needed to be reoptimized using the higher basis set B3LYP/6-31G* and then undergo freqency calculations.
Chair - B3LYP/6-31G(D) Optimization
The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the optimization.
Point Group: C2h
Total Energy: -234.55698536 a.u.
Chair - B3LYP/6-31G(D) Frequency Analysis
The optimized Chair TS underwent frequency analysis. The calculation was then run on a HPC server and the D-Space publication of the frequency analysis can be found here.
Low frequencies --- -564.9382 -0.0006 -0.0003 0.0006 21.3168 26.5951 Low frequencies --- 39.4745 194.3347 268.6930 ****** 1 imaginary frequencies (negative Signs) ******
The lowest "real" normal mode is found to occur at 39.4745cm-1
Sum of electronic and zero-point Energies= -234.414924 Sum of electronic and thermal Energies= -234.409005 Sum of electronic and thermal Enthalpies= -234.408061 Sum of electronic and thermal Free Energies= -234.443808
Boat - B3LYP/6-31G(D) Optimization
The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
Below is a 3-dimensional model of the molecule.
Vibration |
The following data was gathered from the optimization.
Point Group: C2v
Total Energy: -234.54309333 a.u.
Boat - B3LYP/6-31G(D) Frequency Analysis
The optimized Boat TS underwent frequency analysis. The calculation was then run on a HPC server and the D-Space publication of the frequency analysis can be found here.
Low frequencies --- -530.4031 -9.2275 0.0007 0.0008 0.0010 15.5149 Low frequencies --- 17.8691 135.4595 261.5371 ****** 1 imaginary frequencies (negative Signs) ******
The lowest "real" normal mode is found to occur at 17.8691cm-1
Sum of electronic and zero-point Energies= -234.402342 Sum of electronic and thermal Energies= -234.396007 Sum of electronic and thermal Enthalpies= -234.395063 Sum of electronic and thermal Free Energies= -234.431753
Energy Summary
A summary of the total energies in each system after each optimization at a given temperature (data from all analysis above).
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy (a.u.) | Sum of electronic and zero-point energies at 0 K (a.u.) | Sum of electronic and thermal energies at 298.15 K (a.u.) | Electronic energy (a.u.) | Sum of electronic and zero-point energies at 0 K (a.u.) | Sum of electronic and thermal energies at 298.15 K (a.u.) | |
| Chair TS | -231.6193 | -231.4667 | -231.4613 | -234.5570 | -234.4149 | -234.4090 |
| Boat TS | -231.6028 | -231.4509 | -231.4453 | -234.5431 | -234.4023 | -234.3960 |
| Reactant (anti2/Ci) | -231.6925 | -231.5395 | -231.5327 | -234.6117 | -234.4692 | -234.4619 |
(all figures are to 4 d.p)
- 1 a.u. = 1 hartree = 627.509 kcal/mol
Activation energies
| HF/3-21G at 0 K (ΔE (kcal/mol)-1) | HF/3-21G at 298.15 K (ΔE (kcal/mol)-1) | B3LYP/6-31G* at 0 K (ΔE (kcal/mol)-1) | B3LYP/6-31G* at 298.15 K (ΔE (kcal/mol)-1) | Experimental values[5] (ΔE (kcal/mol)-1) | |
| ΔE (Chair) | 45.7 | 45.3 | 34.1 | 33.7 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.6 | 50.3 | 42.0 | 37.6 | 44.7 ± 2.0 |
Although using higher level basis sets on the TSs does not change their geometry, the total energy of the system is stabilised. From the above table it can be seen that using the higher level method ( B3LYP/6-31G(D)) on both chair and boat transition structures produces activation energies which correlate better with experimental values in comparison to the HF/3-21G method.
Looking at the activation energies above, it is clear to see that the reaction is likely to proceed via the chair TS due to the lower activation energy. The chair structure has a lower activation energy because it's a less hindered state[6].
It can also be seen that the activation energy for the Chair TS is very close to the experimental value, showing just how accurate computational chemistry can be.
A final thing to note is that as predicted by theory the sum of electronic and zero-point energies of the structures are lower than the sum of electronic and thermal energies. This is because at 0K there would be no thermal vibrations.
The Diels-Alder Cycloaddition
The Diels-Alder Cycloaddition is part of a family of peri-cyclic (addition/elimination) reactions. The Diels-Alder reaction proceeds via a single six membered transition state which can have two possible conformations, an Endo and an Exo conformation[7]. It is a thermally driven, π4s + π2s cycloaddition involving a conjugate cis diene and an alkene/dienophile, the diene has to be in a cis conformation in order to allow favorable overlap between the reactants. The HOMO/LUMO of the reactants interact with each other to form two new σ bonds and a new π bond. Electron-donating (EDG)/electron-withdrawing (EWG) groups are usually used to govern the rate/characteristics of the reaction.
Below is an image illustrating the general relationship between the two reactants.

A thing to note is that depending on the EWG or EDG on each reactant, the HOMO and LUMO orbitals from either reactant can interact.
The Diels-Alder Cycloaddition of Butadiene and Ethene
Optimization of cis-Butadiene & Ethene
Cis-Butadiene was drawn in GaussView and then optimised using the AM1 semi-empirical molecular orbital method. The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
The following data was gathered from the optimization.
Point Group: C2v
Energy (RAM1): 0.04879718 a.u.
Ethene was drawn in GaussView and then optimised using the AM1 semi-empirical molecular orbital method. The calculation was then run on GaussView since the molecule was small and the .log file of the optimization can be found here.
The following data was gathered from the optimization.
Point Group: D2h
Energy (RAM1): 0.02619024 a.u.
The Molecular Orbitals of Optimized cis-Butadiene and Ethene
The reason these molecules were optimized was so that the symmetry for each reactants HOMO/LUMO could be considered so as to decide if the reaction is allowed or not.
| Cis-Butadiene | Ethene | ||||
| HOMO | LUMO | HOMO | LUMO | ||
| Molecular Orbital |  |
 |
 |

| |
| Symmetry | Antisymmetric | Symmetric | Symmetric | Antisymmetric | |
| Energy/a.u | -0.344 | 0.017 | -0.388 | 0.053 | |
The above table shows how due to symmetry constraints only HOMO-LUMO interactions are allowed/possible. LUMO-LUMO and HOMO-HOMO interactions cannot occur do to symmetry mismatch.
Frequency analysis was carried out on these optimized structures. Ethene showed no negative frequencies, confirming that a minimum had been reached, however, cis-Butadiene showed a negative frequency at -35.89cm-1. This could have been caused by rotation about the backbone C-C bond that occurs readily at room temperature. This conformer of Butadiene may not be the most stable,however, it is the reactive conformer in respect to this Diels-Alder reaction. The presence of a negative frequency suggests that the optimized structure is at a maximum, which is as expected, since the syn-periplanar arrangement results in a noticeable A1,4 strain.
Transition State Optimization and Analysis
Guessing the Transition State
The two optimized structures of Cis-Butadiene and ethene were placed 2.2Å away from each other in GaussView. Using the Frozen Co-ordinate method implemented earlier the terminal carbons of each molecule were frozen and the transition state was then optimised using the AM1 semi-empirical molecular orbital method. After, the bond co-ordinates were unfrozen and the hessian force constant matrix was computed using a TS berny optimization method to perform an Opt+Freq calculation using the same basis set. The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
The following data was gathered from the optimization.
Point Group: C1
Energy (RAM1): 0.11165519 a.u.
A 3-D model of the transition state can be found
Low frequencies --- -955.0032 -7.6989 -5.8876 -0.0049 -0.0031 0.0205 Low frequencies --- 4.1403 146.5954 246.8236 ****** 1 imaginary frequencies (negative Signs) ******
An imaginary frequency was found to occur at -955.0032cm-1 which suggests the formation of a transition state structure.
Sum of electronic and zero-point Energies= 0.253276 Sum of electronic and thermal Energies= 0.259455 Sum of electronic and thermal Enthalpies= 0.260399 Sum of electronic and thermal Free Energies= 0.224012
"Forming" bond lengths: 2.12Å (to 3 s.f)
The vibration corresponding to the imaginary frequency at -955.0032cm-1 was also found to be that of the Diels-Alder cycloaddition via the six membered transition state
From the above image we can see how the ethene molecule comes in from below the butadiene in order to align the orbitals with HOMO/LUMO of each molecule with the correct symmetry so they can interact to form bonds.
The transition state terminal bond length was found to be relatively large in comparison to literature, showing that a C-C bond has not yet formed(C-C sp3-sp3: 1.53 Å, C-C sp2-sp2: 1.46 Å (butadiene); 1.3 3Å (ethene), Van der Waals radius(C): 1.70Å[8]). However, the terminal bond length was found to be less than two the Van der Waals radius of a C atom, suggesting the orbitals are interacting somewhat. Further confirming that this is indeed a transition state for the cycloaddition.
The following image compares the obeserved transition structure bond lengths with the literature values for sp3 and sp2 C bond lengths:
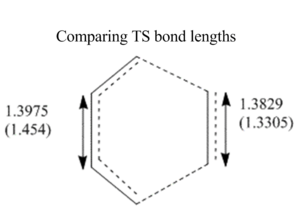
The new C=C bond can be seen to be forming as the bond length of butadiene's bond gets shorter and the ethene's C=C gets longer to form the product hexene.
MO Analysis
| HOMO | LUMO | |
| Molecular Orbital | 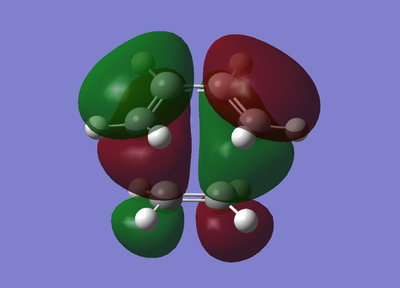 |

|
| Energy/a.u. | -0.324 | 0.023 |
| Symmetry | Antisymmetric | Symmetric |
It is clear to see from the antisymmetric shape of the HOMO above that the overlap of the HOMO of cis-butadiene and the LUMO of ethene formed the HOMO of this transition state. The images of the MO show the C-C σ bonding orbitals of the formed in the reaction. From the shape of the LUMO it is clear to see that this MO was formedfrom the combination of the HOMO of ethene and the LUMO of cis-butadiene. Once again, the above image of the LUMO shows the formation of the σ* antibonding orbitals.
To conclude, this diagram is confirms the previous discussion on the orbital symmetry required to have feasible overlap. Orbitals of the same symmetry have paired up to form new MOs.
Cyclohexa-1,3-diene and Maleic Anhydride (Study of Regioselectivity)
The Diels-Alder cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride, typically proceeds to give the endo adduct under kinetic control as the major product in a 99:1 ratio [9] suggesting that the exo transition structure has a higher energy than the endo TS. Using computational chemistry techniques the aim is to understand exactly why the endo adduct is the preferred product.

Optimization of Reactants
Cyclohexa-1,3-diene and Maleic Anhydride were drawn in GaussView and then optimised using the AM1 semi-empirical molecular orbital method. The calculation was then run on a HPC server and the D-Space publication of the optimization of Cyclohexa-1,3-diene can be found here and the publication for Maleic Anhydride can be found here.
The reactants were optimized so the LUMO/HOMO of each molecule could be observed. Then whether or not the MOs would interact to form a stable product could be determined. As with the case of cis-Butadiene & Ethene, only orbitals of the same symmetry can interact (the cyclohexadiene LUMO and the maleic anhydride HOMO, to form an overall symmetric product, or the cyclohexadiene HOMO and the maleic anhydride LUMO, to form an overall antisymmetric product) to form a plausible TS.
| Cyclohexa-1,3-diene | Maleic Anhydride | |||
| HOMO | LUMO | HOMO | LUMO | |
| Molecular Orbital | 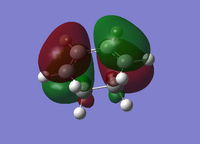 |
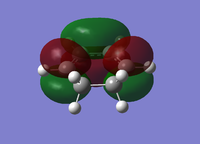 |
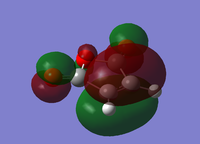 |
|
| Energy/a.u. | -0.3256 | 0.0138 | -0.4419 | -0.0595 |
| Symmetry | Antisymmetric | Symmetric | Symmetric | Antisymmetric |
Optimization of Transition States
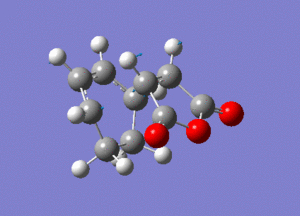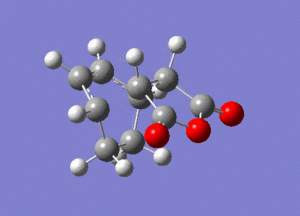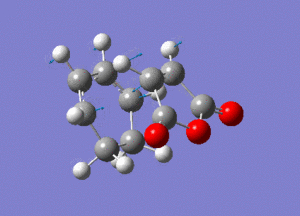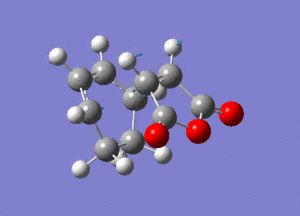
Analysis of the Exo TS
The two optimized structures of Cyclohexa-1,3-diene and Maleic Anhydride were placed 2.2Å away from each other in the Exo orientation in GaussView. Using the Frozen Co-ordinate method implemented earlier the 4 carbons involved in the bond forming were frozen and the transition state was then optimized using the AM1 semi-empirical molecular orbital method. After, the bond co-ordinates were unfrozen and the hessian force constant matrix was computed using a TS berny optimization method to perform an Opt+Freq calculation using the same basis set. The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
The following data was gathered from the optimization.
Point Group: C1
Energy (RAM1): -0.05041906 a.u.
(The Exo state has a less negative energy than the Endo state, therefore is less favored)
Low frequencies --- -812.5227 -0.3597 -0.1544 -0.0048 2.9187 4.0604 Low frequencies --- 5.5351 61.0283 124.0240 ****** 1 imaginary frequencies (negative Signs) ******
An imaginary frequency was found to occur at -812.5227cm-1 which suggests the formation of a transition state structure.
Sum of electronic and zero-point Energies= 0.134882 Sum of electronic and thermal Energies= 0.144881 Sum of electronic and thermal Enthalpies= 0.145825 Sum of electronic and thermal Free Energies= 0.099124
"Forming" bond lengths: 2.17Å (to 3 s.f)
The vibration corresponding to the imaginary frequency at -812.5227cm-1 was also found to be that of the Diels-Alder cycloaddition via the Exo TS.
In the following analysis, the direction of the IRC was chosen as the forward reactions due to the fact that this reaction is symmetrical. The optimized chair TS was used and the force constants for 50 points were all calculated.
The calculation was then run on a HPC server and the D-Space publication of the analysis can be found here.
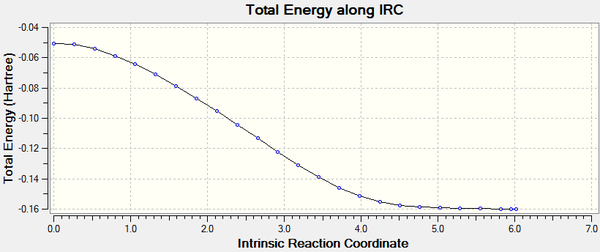
Activation Energy (ΔE (kcal/mol)-1): 68.70
(This reaction proceeds via concerted bond formation to form two new C-C σ bonds at the loss of 2 π bonds)
Analysis of the Endo TS
The two optimized structures of Cyclohexa-1,3-diene and Maleic Anhydride were placed 2.2Å away from each other in the Endo orientation in GaussView. Using the Frozen Co-ordinate method implemented earlier the 4 carbons involved in the bond forming were frozen and the transition state was then optimized using the AM1 semi-empirical molecular orbital method. After, the bond co-ordinates were unfrozen and the hessian force constant matrix was computed using a TS berny optimization method to perform an Opt+Freq calculation using the same basis set. The calculation was then run on a HPC server and the D-Space publication of the optimization can be found here.
The following data was gathered from the optimization.
Point Group: C1
Energy (RAM1): -0.05150480 a.u.
Low frequencies --- -807.1405 -0.8736 -0.2615 -0.0104 0.8959 1.7321 Low frequencies --- 2.4989 62.4809 111.7886 ****** 1 imaginary frequencies (negative Signs) ******
An imaginary frequency was found to occur at -807.1405cm-1 which suggests the formation of a transition state structure.
Sum of electronic and zero-point Energies= 0.133495 Sum of electronic and thermal Energies= 0.143683 Sum of electronic and thermal Enthalpies= 0.144627 Sum of electronic and thermal Free Energies= 0.097353
"Forming" bond lengths: 2.16Å (to 3 s.f)
The vibration corresponding to the imaginary frequency at -807.1405cm-1 was also found to be that of the Diels-Alder cycloaddition via the Endo TS.
In the following analysis, the direction of the IRC was chosen as the forward reactions due to the fact that this reaction is symmetrical. The optimized chair TS was used and the force constants for 50 points were all calculated.
The calculation was then run on a HPC server and the D-Space publication of the analysis can be found here.

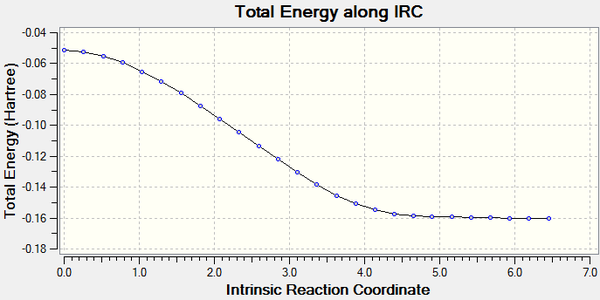
Activation Energy (ΔE (kcal/mol)-1): 68.19
(This reaction proceeds via concerted bond formation to form two new C-C σ bonds at the loss of 2 π bonds)
The activation E via the Exo TS is higher than that off the Endo TS suggesting that the rate of formation of Endo adduct would be faster, explaining the regioselectivity of this reaction when under kinetic control
Comparison
The edited image below compares the bond lengths of the two adducts
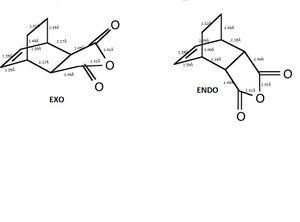
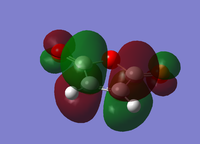
| Endo Conformer | Exo Conformer | |||
| HOMO | LUMO | HOMO | LUMO | |
| Molecular Orbital | 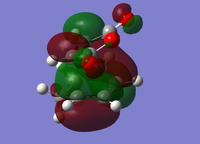 |
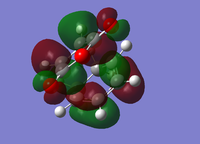 |
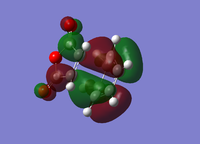 |
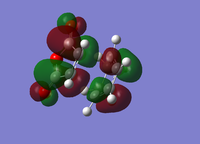
|
| Energy/a.u. | -0.3451 | -0.0357 | -0.34279 | -0.0404 |
| Symmetry[10] | Antisymmetric | Antisymmetric | Antisymmetric | Antisymmetric |
The fact that the HOMO/LUMO of both adducts are anti symmetric suggests that it's the HOMO of Cyclohexa-1,3-diene that interacts with the LUMO of Maleic Anhydride.
The MOs suggest that the preferred adduct should be the Exo form over the Endo form. In the HOMO for the endo adduct the antibonding π* orbitals on the oxygens in the C=O are seen to be in a repulsive interaction with the antibonding π* orbitals of the C=C bonds on cyclohexadiene section of the molecule, suggesting why the endo form has it's shape, but also increasing the strain of the molecule. The exo form does not have this repulsive interaction suggesting it should be the more stable adduct[11].
Although, the endo TS is lower in energy than the exo TS (-0.05151 vs -0.05042), the exo adduct is lower overall lower in energy do to not having the unfavorable interactions the endo product has.
This suggests that the exo product is actually the thermodynamic product[12] (most stable) but has a higher activation energy due to it's higher energy TS and lower energy final structure but under kinetic control the pathway with the lowest activation energy and the most stable transition state forms fastest, the Endo form even though it is the least stable product.
The below images displays how secondary orbital interactions stabilise the endo transition state causing it to be lower in energy.
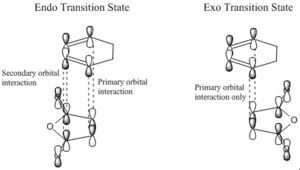
Four of the π orbitals on HOMO of the cyclohexadiene interact with the LUMO of maleic anhydride in the Endo TS compared to only the 2 primary bonding orbitals interacting in the Exo TS, stabilising the TS, making formation of the Endo product more favorable regardless of the strain and steric repulsion found in the adduct.
Conclusions
After completing this project it is easy to understand how powerful computational chemistry can be. With it we can optimize and model any molecule of our choosing, regardless of it's size or complexity and then analyse a reaction and predict which products would form and why, without having to step foot in a lab. This experiment in particular has shown how orbital symmetry is conserved in Diels-Alder cycloadditions and how using frontier molecular orbital theory to model transition states can help us understand how the HOMO of a diene and the LUMO of a dienophile can interact to govern the regiochemistry of the reaction. The power of secondary orbital interactions stabilising transition structures can be seen from the reaction between Cyclohexa-1,3-diene and Maleic Anhydride. Even though the Exo adduct is the less sterically hindered, more stable form, these interactions result in the overwhelming favor of the Endo adduct (a 1:99 ratio for Exo:Endo).
Possible Ammendments
In these calculations solvent effects, temperature and pressure (general environmental effects) are ignored. As an extension to this study it may be wise to explore the effects of temperature and solvent on the secondary orbital interactions or the stabilisation of transition states. Furthermore, if there was more time, it may have been wise to run the calculations using other methods (e.g DFT) to see if the choice of favorable pathway changes.
References
- ↑ A.C. Cope, E.M. Hardy, J. Am. Chem. Soc., 1940, 62, 441–444
- ↑ Olaf Wiest , Kersey A. Black , K. N. Houk, J. Am. Chem. Soc., 1994, 116 (22), pp 10336–10337
- ↑ Olaf Wiest , Kersey A. Black , K. N. Houk, J. Am. Chem. Soc., 1994, 116 (22), pp 10336–10337
- ↑ Lab Script
- ↑ Lab Script
- ↑ Keiji. Morokuma , Weston Thatcher. Borden , David A. Hrovat, J. Am. Chem. Soc., 1988, 110 (13), pp 4474–4475
- ↑ R. Hoffman, Organic Chemistry: An Intermediate Text, 2004, John Wiley & Sons
- ↑ N.C. Craig, P. Groner, D.C. McKean, J. Phys. Chem. A., 2006, 110, 7461-7469.
- ↑ R. Gleiter, M. C. Böhm, Pure & Appl. Chem., 1983, 55, 237—244
- ↑ R.B. Woodward, R. Hoffmann, Angew. Chem. Int. Ed. Engl., 1969, 8, 781–853
- ↑ R. Hoffmann, R.B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388-4389
- ↑ I. Fleming, Frontier Molecular Orbitals and Organic Chemical Reactions, 1976