Rep:MOD:kt916
NH3 Molecule
N-H Bond Distance
1.01798 Angstroms
H-N-H Bond Angle
105.741o
Calculation Method
RB3LYP
Basis set
6-31G(d.p)
E(RB3LYP) Final Energy
-56.55776873 a.u
RMS gradient
0.00000485 a.u
Point Group
C3v
Item Table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Interactive
Ammonia molecule |
The optimisation file is liked to here
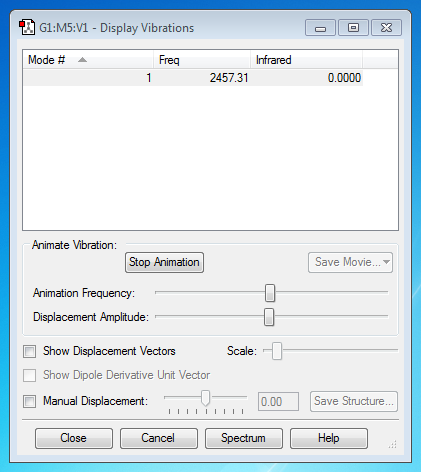
Vibrational Mode(s)
Questions
From the 3N-6 rule, (N=4) the number of expected nodes is 6, which is shown in the picture above.
Modes 2&3 and 5&6 are degenerate.
Modes 1,2,3 are Bending vibrations and Modes 4,5,6 are stretching vibrations.
Mode 4 is highly symmetric
Mode 1 is the umbrella mode.
2 bands would be seen in an experimental spectrum of gaseous ammonia.
The Charges on the Ammonia molecule are as follows:
N = -1.125e
H= 0.375e
Which is expected as N has a greater electronegativity than H.
N2 Molecule
N-N Bond Distance
1.10550 Angstroms
N-N Bond Angle
180 o Linear Molecule
Calculation Method
RB3LYP
Basis set
6-31G(d.p)
E(RB3LYP) Final Energy
-109.52412868 a.u
RMS gradient
0.00000365 a.u
Point Group
DHinf
Item Table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000003 0.001200 YES
Interactive
Nitrogen molecule |
The optimisation file is liked to here
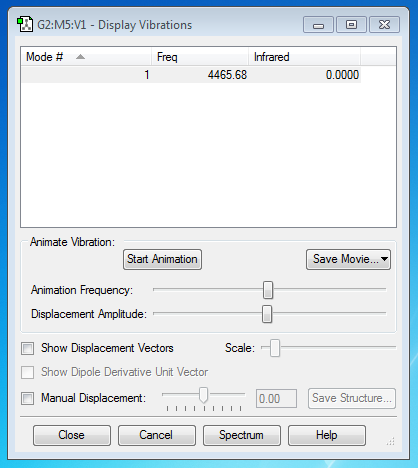
Vibrational Mode(s)
Questions
From the 3N-5 rule, (N=2) the number of expected nodes is 1, which is shown in the picture above.
There is only 1 mode, and it is a symmetric stretching vibration
no band would be seen in an experimental spectrum of Nitrogen. (Diatomic molecule)
The Charges on the Nitrogen molecule are as follows:
N = 0e
Which is expected as both are the same element hence the same electronegavity.
H2 Molecule
H-H Bond Distance
1.10550 Angstroms
H-H Bond Angle
180 o Linear Molecule
Calculation Method
RB3LYP
Basis set
6-31G(d.p)
E(RB3LYP) Final Energy
-1.17853936 a.u
RMS gradient
0.00000017 a.u
Point Group
DHinf
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Interactive
Hydrogen molecule |
The optimisation file is liked to here
Vibrational Mode(s)
Questions
From the 3N-5 rule, (N=2) the number of expected nodes is 1, which is shown in the picture above.
There is only 1 mode, and it is a symmetric stretching vibration
No band would be seen in an experimental spectrum of Nitrogen. (Diatomic molecule)
The Charges on the Hydrogen molecule are as follows:
H = 0e
Which is expected as both are the same element hence the same electronegavity.
Reaction Energies
E(NH3)= -56.55776873 a.u 2*E(NH3)= -113.1155375 a.u E(N2)= -109.52412868 a.u E(H2)= -1.17853936 a.u 3*E(H2)= -3.53561808 a.u ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u or -146.4785879 kJmol-1
The Literature value for the formation of Ammonia gas is -45.94kJ-1 [1]
- ↑ Cox, Wagman, et al., 1984 Cox, J.D.; Wagman, D.D.; Medvedev, V.A., CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., New York, 1984, 1. .
Which is drastically lower than the calculated value above, mainly due to the assumptions made while optimizing the m9olecule, such as the force field methods which is different in reality. Ammonia is thermodynamically more stable than it's reactants (Hydrogen and Nitrogen gas), this can be seen as the change in energy (ΔE) is negative (exothermic).
CN- Ion
C-N Bond Distance
1.18409 Angstroms
C-N Bond Angle
180o
Calculation Method
RB3LYP
Basis set
6-31G(d.p)
E(RB3LYP) Final Energy
-92.82453153 a.u
RMS gradient
0.00000704 a.u
Point Group
Cinfv
Dipole Moment
0.5236 Debye
Item Table
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000005 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Interactive
Cynaide Ion |
The optimisation file is liked to here
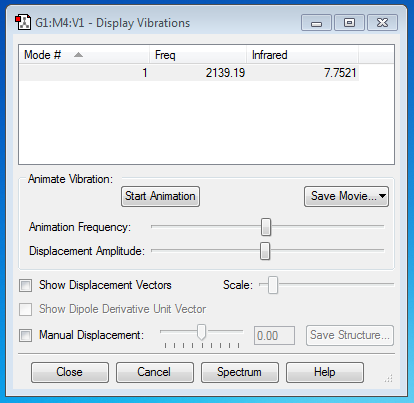
Vibrational Mode(s)
Questions
From the 3N-5 rule, (N=2) the number of expected nodes is 1, which is shown in the picture above.
The single mode is a symmetric stretch.
1 band would be seen in an experimental spectrum of gaseous ammonia.
The Charges on the Cyanide Ion are as follows:
C = -0.246e
N = -0.754e
Which is expected as N has a greater electronegativity than C (3.04 and 2.55 respectively), and the charges add up to -1e, which is the total charge of the Ion.
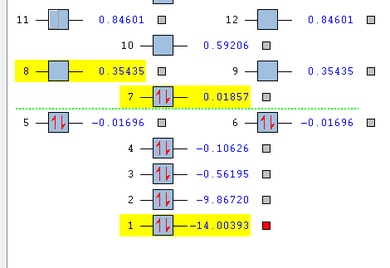
Molecular Orbitals for CN-
Bond order=3
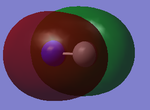
1s orbitals
This picture shows the first 12 Orbitals of the CN- ion, in which the first 7 are occupied.
Below are the first 2 orbitals.
These are the 1s orbitals for both Nitrogen and Carbon (numbered 1 and 2), Nitrogen being lower in energy at -14.00393 a.u and carbon at -9.86720 a.u. There are no interactions between the atomic orbitals, as all the electron density is concentrated at one atom. The nitrogen 1s is expected to have the lower energy due to it's greater electronegavitiy, hence it holds it's electrons closer to the nucleus, making it more stable.
2s orbitals
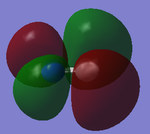
The images above show the 2σg (bonding) and 2σ*u (anti-bonding) molecular orbitals (numbered 3 and 4).
The 2σg molecular orbital is caused by the overlap of the 2s atomic orbitals (in phase) from both carbon and nitrogen, this is the same for the 2σ*u, however, the atomic orbitals are out of phase.
2p orbitals
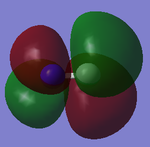
The images above shows two bonding 1πu orbitals (numbered 5 and 6), which are degenerate in energy and two anti-bonding 1π*u orbitals (numbered 8 and 9 which are the LUMOs), which arealso degenerate in energy
The 1πu molecular orbitals come from the overlap of 2p atomic orbitals of C and N in phase, while the anti-bonding (higher in energy due to electron density not being between the Molecule) have the overlaps out of phase, the orbitals in this case the 2px and 2py atomic orbitals. They are degenerate in energy due to all p orbitals being degenerate (in each atom).
3s orbitals
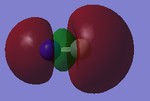
The images above shows the bonding 3σg orbital (also the HOMO) and the anti-bonding 3σ*u (numbered 7 and 10 respectively).
These molecular orbitals,are caused by the overlap of the 2pz orbitals in both C and N, in which the bonding is in phase while anti-bonding isn't. The Molecular orbitals are not perfectly symmetrical because there is a difference in energy between the p orbitals of carbon and nitrogen, Nitrogen being lower due to it's greater electronegavity. There is also some mixing of the orbitals as well (sp hybridization).