Rep:MOD:hly3614

==

Introduction

Potential Energy Surface (PES)

A potential energy surface (PES) is an energy 'landscape' that interpretates the total energy of a molecule as a function of molecular geometries based on Born-Oppenheimer Approximation. According to the fact that a polyatomic molecule often has 3N-6 ( N= Number of atoms and N>2 ) geometric degrees of freedom, the PES is likely to possess 3N-6 dimensions but is usually reduced to 3-D representation.

A Minimum And A Transition State

A minimum on the PES corresponds to a stationary point where the gradient of the energy curve (i.e the first derivative) is zero and the curvature (i.e the second derivative) reflects that any change being made to this point leads to an increase of energy, whereas a transition state is a saddle point at which the change of total energy with respect to the change of geometry is zero but in terms of curvature, moving away from the point, the energy drops in one direction.

Relevant Gaussian Calculations

A geometry optimization in Gaussian helps find out the stationary points (i.e gradient=0) by calculating the first derivatives of the energy curve and the frequency calculations are used to obtain information about the curvature of the points (i.e the second derivative) by calculating harmonic frequencies of the polyatomic molecule, confirming whether a minimum or a transition state is reached, based on the fact that all the vibrational frequencies for a minimum are real numbers whereas an imaginary frequency occurs for a transition structure.

Nf710 (talk) 23:19, 14 December 2016 (UTC) That is a nice way of interpret it, but the correct way is to say that you taking the second derivatives

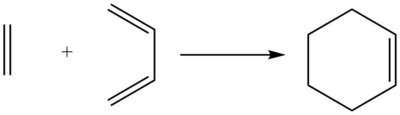
Exercise 1: Reaction of Butadiene with Ethylene

Reaction Scheme

Frontier Molecular Orbital Analysis

Fig. 1: MO Diagram of Butadiene/Ethylene TS

Fig. 2: MO Diagram for an example of cycloaddtion with normal electron demand ^[1]

Molecule and orbital:	MOs:	Symmetry [gerade/ungerade (g/u for short)]:
Butadiene, HOMO		g
Butadiene, LUMO		u
Ethene, HOMO		u
Ethene, LUMO		g
Butadiene/ethylene Transition state, HOMO		u
Butadiene/ethylene Transition state, LUMO		u
Butadiene/ethylene Transition state, 2nd HOMO		g
Butadiene/ethylene Transition state, 2nd LUMO		g

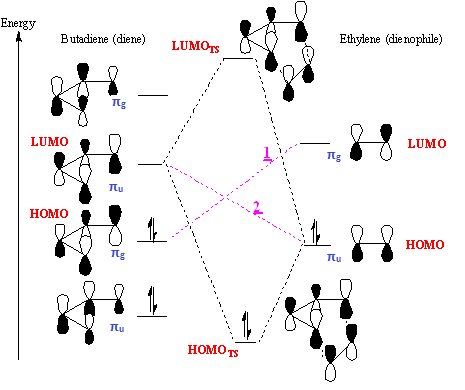
According to the results of Gaussian calculations, the HOMO of the transition state is formed from the LUMO of the butadiene and the HOMO of the ethylene, both of which have the π_u symmetry. Theoretically, however, as illustrated in Fig 2, a Diels-Alder Reaction with normal electron demand favours the interaction between the HOMO of diene and the LUMO of the dienophile due to a smaller energy gap and better orbital overlap. In the case of Fig.2, the small energy gap results from attaching an electron withdrawing group to the dienophile substrate that lowers its LUMO energy. This can be further enhanced by making the diene substrate more electron-rich, leading to a higher energy HOMO. The inconsistency of the computed results is likely to arise from the fact that the unsubstituted butadiene and ethylene are not a good diene and not a good dienophile respectively to ensure the normal energy match. As for symmetry, interacting orbitals also need to have the same symmetry to allow a non-zero orbital overlap, so the g-g and u-u interactions are symmetry allowed whereas a g-u interaction is symmetry disallowed because the orbital overlap integral is equal to zero.

C-C Bond Length Analysis

Changes in Bond Lengths:

Molecule:	Illustration:	C-C Bond Lengths/Å:
Butadiene		C1-C2=1.33531 C2-C3=1.46835 C3-C4=1.33531
Ethene		C5-C6=1.32731
Transition State		C1-C2=1.37977 C2-C3=1.41110 C3-C4=1.37979 C4-C6=2.11469 C6-C5=1.38177 C5-C1=2.11479
Product		C1-C2=1.50034 C2-C3=1.33766 C3-C4=1.50034 C4-C6=1.54004 C6-C5=1.54076 C5-C1=1.54003

[The bond lengths are measured by extracting the bond lengths of corresponding optimized structures in GaussView.]
Representative C-C bond lengths with respect to hybridization/Å:

sp3-sp3	sp3-sp2	sp2-sp2
literature value[2]: 1.54Å computed value: 1.54Å	literature value[2]: 1.50Å computed value: 1.50Å	literature value[2]: 1.47Å computed value: 1.47Å (except C2=C3 in the product = 1.34Å)

By comparing the computed bond lengths with the literature values, the C=C double bonds (C₁-C₂, C₃-C₄, C₅-C₆) in both of the reactants start to elongate until eventually become single bonds in the product during the reaction, while the previous C-C single bond in butadiene (C₂-C₃) is shortend to form a double bond although the bond length is slightly shorter than expected. This might be due to the ring strain leading to a distortion of the bond. Also, based on an appropriate trajectory of the reactants, two new single bonds (C₄-C₆ and C₅-C₁) are formed with typical sp3 C-C bond lengths of 1.54Å via a transition state where the distances between the butadiene terminal carbons and the ethylene carbons are appox. 2.11Å. A typical Van der Waals' radius of a carbon is ~1.70Å ^[3], and by looking at the IRC profile, the two reactants start to approach each other from a distance of ~3.41Å, which is approximately twice of the Van der Waals' radius. The computed distance of 2.11Å at transition state lying in between the Van der Waals' distance of ~3.41Å and the final bond lengths of 1.54Å indicates a partially formed C-C single bond at the transition state.

Vibration at Transition State Corresponding to Reaction Path

Gif 1: Vibration at transition state with an imaginary vibrational frequency: -948.57cm^-1


Gif 2: vibration with first positive vibrational frequency: 145.10cm^-1


The vibration occurring at -948.57cm^-1 in the transition state is illustrated in Gif.1. The negative sign actually represents an imaginary vibrational frequency, which results from solving the square root of a negative force constant, i.e the second derivative (curvature) of the energy curve related to this particular reaction pathway. Since mathematically, a negative second derivative indicates a maximum point, in this case, the negative value occurring at -948.57cm^-1 suggests the vibration of bonds corresponding to an energy maximum in the transition state.

Comparing the vibrations shown in Gif.1 and Gif.2, the vibration occurring at -948.57cm^-1 shows a trend towards bond formation between the butadiene terminal carbons and ethylene carbons, whereas the lowest positive vibration mode indicates the vibrations of the two reactant molecules are rather in two parallel planes without any interactions to allow a bond formation.

In addition, the illustration of the vibration at -948.57cm^-1 suggests that the formation of the 2 bonds is synchronous, but an IRC animation makes the idea of this concerted reaction more evident:

gif 3: IRC Animation of the Diels-Alder reaction of butadiene/ethylene

CLever use of IRC to identity this. Good section

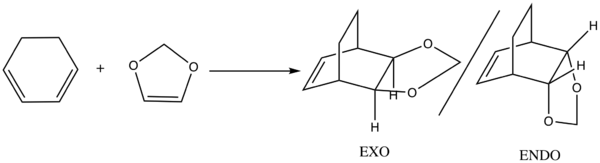
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction Scheme

Frotier Molecular Orbital ( FMO ) Analysis

FMOs of the reactants:

Molecules and Orbitals	Illustration	Symmetry (g/u)
1,3-Dioxole HOMO		u
1,3-Dioxole LUMO		g
Cyclohexadiene HOMO		(distorted)g
Cyclohexadiene LUMO		(distorted)u

Illustration of FMOs during the cyclohexadiene/1,3-Dioxole transition state:

Types of Transition States and FMOs	Illustration [optimized at B3LYP/6-31G(d) level]	Symmetry (g/u)
ENDO HOMO		u
ENDO LUMO		u
EXO HOMO		u
EXO LUMO		u

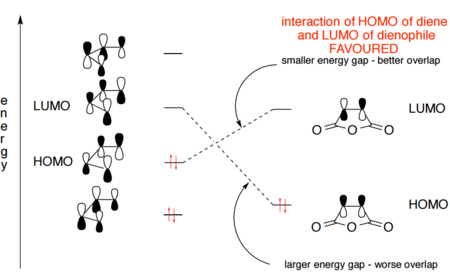
According to the FMOs illustrated above, the HOMOs and LUMOs of both ENDO and EXO transition states are dominated by the interactions between the HOMO of 1,3-Dioxole and the LUMO of cyclohexadiene, both of which have a π_u symmetry. Therefore ENDO and EXO transition states also have π_u symmetries. This computed result refers to an inverse electron demand, which is likely due to the fact that being attached to two electron donating groups (i.e the O atoms ) makes 1,3-dioxole a very poor dienophile with a high energy LUMO and thus making the LUMO of dienophile and HOMO of diene too far in energy to interact.

Analysis on The Reaction Barrier ΔG† and The Reaction Energy ΔG

Sum of Electronic and Thermal Free Energies at each stage during the reaction

Molecules	Sum of Electronic and Thermal Free Energies/ Hartrees/Particle	Sum of Electronic and Thermal Free Energies ×627.5095×4.184 / KJ/mol
1,3-Dioxole	-267.068132	-701187.3133
Cyclohexadiene	-233.324375	-612593.0878
ENDO TS	-500.332149	-1313621.931
EXO TS	-500.329168	-1313614.105
ENDO PROD	-500.418691	-1313849.147
EXO PROD	-500.417322	-1313845.553

• Unit conversion:

The way to convert unit from Hartree/particle to KJ/mol is by multiplying constants 627.5095 and 4.184 ^[4]

• Calculating Reaction Barrier ΔG†:

ΔG†= [G_TS - (G_{cyclohexadiene}+ G_dioxole)] <eq.a>

• Calculating Reaction Energy ΔG:

ΔG= [G_Product - (G_{cyclohexadiene}+ G_dioxole)] <eq.b>

Therefore, based on the computed results and the calculation methods listed above:

	For ENDO	For EXO
ΔG†/KJ/mol	+158.47	+166.30
ΔG/KJ/mol	-68.75	-65.15

The ENDO product turns out to be both kinetically and thermodynamically more favored as it can be reached via the lowest transition barrier among the three, and can lead to the lowest energy product as well.
Secondary Orbital Interactions
Having all of the pi systems aggregated close in space, the ENDO transition state is expected to be more sterically clashed than the EXO TS and high in energy. However, the lower reaction barrier via an ENDO transition state can be explained by the secondary orbital interactions since a strong, in-phase orbital overlap is easily observed from the HOMO of the ENDO transition state. The dominant secondary orbital interaction between the p orbitals on O atoms and C atoms stablizes the HOMO of the ENDO TS, lowering the activation barrier and yielding the kinetically more stable ENDO product formation.

Nf710 (talk) 23:58, 14 December 2016 (UTC) Your energies are correct with the correct reasoning, try not to us u and g for symmetry. as the group theory behind those symmetry labels requires a center of inversion.

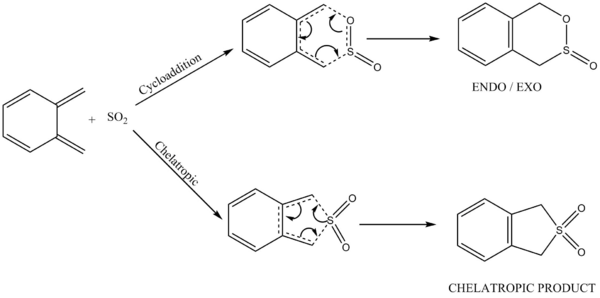
Exercise 3: Diels-Alder vs Cheletropic

Reaction Scheme

Optimized Transition Structure at PM6 Level

Reaction Pathways	Optimized TS
EXO Cycloaddition	Vibrational frequency at TS = -351.77cm-1
ENDO Cycloaddition	Vibrational frequency at TS = -334.39cm-1
Chelatropic Reaction	Vibrational frequency at TS = -486.71 cm-1

Visualising reactin coordinates: IRC of The Three Possible Pathways

Reaction Pathways	IRC
EXO Cycloaddition
ENDO Cycloaddition
Chelatropic Reaction

The animation of IRCs illustrates that during all pathways, as the SO₂ approaches close enough to the xylylene, the pi electrons in the 6-membered ring in xylylene starts to conjugate across the system and eventually the 6-membered ring becomes aromatic.
Besides, the IRC also indicates a concerted reaction for the chelatropic pathway, whereas the formation of C-S and C-O in both of the cycloaddition pathways are asynchronous. The reason why the formation of C-S follows the C-O bond formation is that since S atom is likely to have a larger Van der Waals' radius than O, it approaches the xylylene from a further distance than O.

Calculating the Reaction Barriers ΔG† and the Reaction Energies ΔG

Sum of Electronic and Thermal Free Energies at each stage during the reaction

Molecules	Sum of Electronic and Thermal Free Energies/ Hartrees/Particle
SO2	-0.119267
xylylene	0.178545
ENDO TS	0.090562
EXO TS	0.092078
Chelatropic TS	0.099062
ENDO PROD	0.021703
EXO PROD	0.021452
Chelatropic PROD	0.000001

Therefore, based on the computed results and the calculation methods listed in Exercise 2, eq.a and eq.b:
Calculating Reaction Barrier ΔG†: ΔG†= [G_TS - (G_{cyclohexadiene}+ G_dioxole)]×627.5095×4.184 / KJ/mol <eq.a>
Calculating Reaction Energy ΔG: ΔG= [G_Product - (G_{cyclohexadiene}+ G_dioxole)]×627.5095×4.184 / KJ/mol <eq.b>
the ΔG† and ΔG are calculated:

	For ENDO	For EXO	For Chelatropic
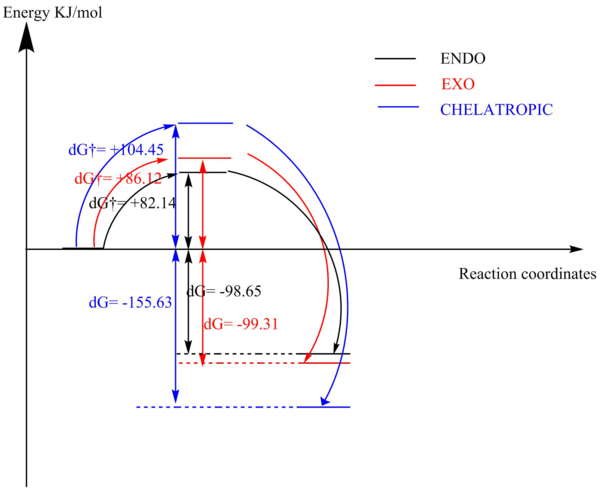
ΔG†/KJ/mol	+82.14	+86.12	+104.45
ΔG/KJ/mol	-98.65	-99.31	-155.63

Based on the calculations, the ENDO Diels-Alder Reaction is kinetically preferred as it has the lowest reaction barrier among the three pathways, while the Chelatropic product is thermodynamically most stable due to a much lower energy level of product than the others.

Reaction Profiles for the three possible pathways

(Don't use curved arrows that go backwards Tam10 (talk) 14:22, 6 December 2016 (UTC))

Reaction beween SO₂ and the second s-cis diene fragment

IRC For ENDO Cycloaddition

IRC For EXO Cycloaddition

After calculating the reaction barrier and reaction energies, it turns out that both of the ENDO and EXO pathways result in high reaction barriers and higher energies of products comparing with the reactions with the outside diene substrates. Therefore the reactions with the second diene are both thermodinamically and kinetically disfavored.

Conclusion

To sum up, different calculation methods of choice using Gaussian allows us to locate (by geometry optimization and frequency calculations), visualize (by extracting the IRC) and extract various information about particular reaction pathways (by checking the MOs for HOMO-LUMO interactions) on a PES. However, the program can only make predictions based on various theoretical approximations and models in quantum mechanics, the results of which are possible to disagree with experimental observations that are affected by a lot of other factors such as solvent, temperature, pH and so on. Also, the Gaussian calculations can be time consuming because complicated calculations can be established according to the calculation methods of choice.

Reference

[1] Lecture Handout 2; Sue Gibson; 2nd year Pericyclic Reactions; [2] [[1]] [3] [[2]]