Rep:MOD:dhk3517
NH3 optimization
Summary
Molecule NH3 Calculation method RB3LYP Basis Set 6-31G(d,p) E(RB3LYP) -56.55776873 a.u. RMS Gradient Norm 0.00000485 a.u. Point Group C3V
Geometric Information
Optimized bond distance (N-H) = 1.01798Å
Optimized bond angle (H-N-H) = 105.741°
Items
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986281D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Jmol dynamic image of NH3
NH3 |
Link to completed NH3 optimization
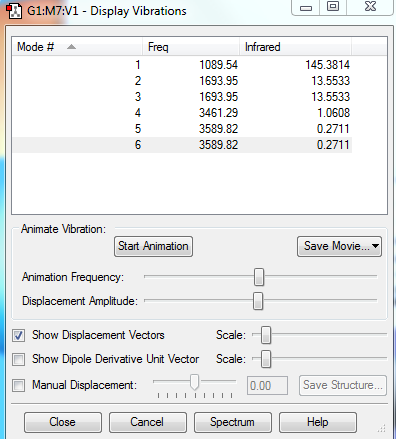
Vibrational Analysis
1.How many modes do you expect from the 3N-6 rule?
3(4)-6 = 6 modes
2.Which modes are degenerate (i.e. have the same energy)?
2 and 3, 5 and 6 The two pairs have the same frequency which means they are of same energy.
3.Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Bending: 1,2,3 as the vibrations cause a change in bond angles Stretching: 4,5,6 as the vibrations cause a change in bond lengths
4.Which mode is highly symmetric?
1: All three bonds bend simultaneously with the same angle in the same direction 4: All three bonds stretch to the same extent simultaneously
5.One mode is known as the "umbrella" mode, which one is this?
1: The three bonds bend down and up simultaneously like an umbrella
6.How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
2(at 1089.54cm-1, 1693.95cm-1): Although there are 6 modes of vibrations and 4 different frequencies, the vibrations at 3461.29cm-1, 3589.82cm-1 are IR inactive as they have no change in dipole. The two bands are due to 1800cm-1: H-N-H scissoring, 1000cm-1: N-H wagging.[1].
Charge analysis
Charge on N-atom: -1.125
Charge on H-atom: 0.375
Negative charge is expected on the N-atom as it is more electronegative than the H-atoms, drawing the electrons towards itself. As a result, the positive lies on the H-atom.
N2
Summary
molecule N2 Calculation Method RB3LYP Basis Set 6-31G(d,p) E(RB3LYP) -109.52412868 a.u. RMS Gradient Norm 0.00000365 a.u. Point Group D*H
Geometric Information
Bong length: 1.10550Å
Bond angle: 180°
Items
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000002 0.001800 YES
RMS Displacement 0.000003 0.001200 YES
Predicted change in Energy=-1.248809D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Jmol dynamic image of N2
N2 |
Link to completed N2 optimization
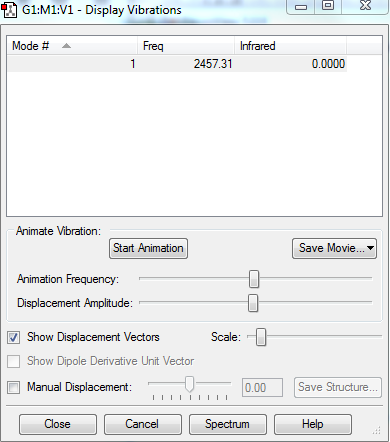
Vibrational Analysis
1.How many modes do you expect from the 3N-5 rule?
3(2)-5 = 1 mode
2.Which modes are "bending" vibrations and which are "bond stretch" vibrations?
1: Stretching as the bond lengths are changing
3.Which mode is highly symmetric?
1 as the two atoms are stretching in and out simultaneously to the same extent.
4.How many bands would you expect to see in an experimental spectrum of gaseous nitrogen?
Although the molecule vibrates at 2457.31cm-1, there will be no bands seen in the experimental spectrum as there is no change in dipole moment in this symmetrical molecule, resulting the molecule to be IR inactive.
Charge analysis
Charge on N atoms: 0
H2
Summary
Molecule H2 Calculation Method RB3LYP Basis Set 6-31G(d,p) E(RB3LYP) -1.17853930 a.u. RMS Gradient Norm 0.00012170 a.u. Point Group D*H
Geometric Information
Bond length=0.74309Å
Bond angle=180°
Items
Item Value Threshold Converged?
Maximum Force 0.000211 0.000450 YES
RMS Force 0.000211 0.000300 YES
Maximum Displacement 0.000278 0.001800 YES
RMS Displacement 0.000393 0.001200 YES
Predicted change in Energy=-5.852867D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7431 -DE/DX = -0.0002 !
--------------------------------------------------------------------------------
Jmol dynamic image of H2
H2 |
Link to completed H2 optimization
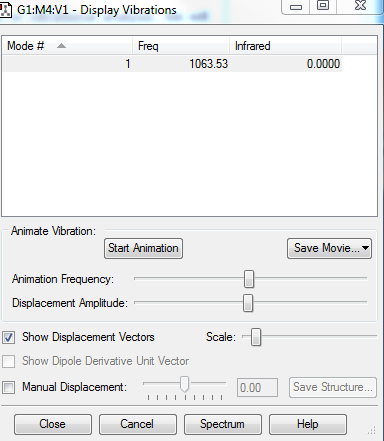
Vibrational Analysis
1.How many modes do you expect from the 3N-5 rule?
3(2)-5 = 1 mode
2.Which modes are "bending" vibrations and which are "bond stretch" vibrations?
1: bond stretch as there is a change in bond lengths
3.Which mode is highly symmetric?
1
4.How many bands would you expect to see in an experimental spectrum of gaseous hydrogen?
Although there is bond stretch at 4461.48cm-1, similar to N2, H2 is a symmetrical molecule with no change in dipole. Hence, it is also IR inactive so there is no band seen in an experimental spectrum.
Charge analysis
charge on H atoms: 0
Calculations of ΔE for NH3
N2+3H2->2NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853930 a.u.
3*E(H2)= -3.53561790 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579088 a.u. = -146.48 kJ/mol
The ammonia product is more stable than the gaseous reactants as the energy change of the reaction is negative, which tells us that the energy of the ammonia product is lower in energy and the gaseous reactants lose energy to form the ammonia product. The lower its energy, the more stable it is. Therefore, ammonia product is more stable than the gaseous reactants.
F2
Summary
Calculation Method RB3LYP Basis Set 6-31G(d,p) E(RB3LYP) -199.49825212 a.u. RMS Gradient Norm 0.00014444 a.u. Point Group D*H
Geometric analysis
Bond length=1.40330Å
Bond angle=180°
Items
Item Value Threshold Converged?
Maximum Force 0.000250 0.000450 YES
RMS Force 0.000250 0.000300 YES
Maximum Displacement 0.000308 0.001800 YES
RMS Displacement 0.000435 0.001200 YES
Predicted change in Energy=-7.696489D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4033 -DE/DX = -0.0003 !
--------------------------------------------------------------------------------
Jmol dynamic image of F2
F2 |
Link to completed F2 optimization
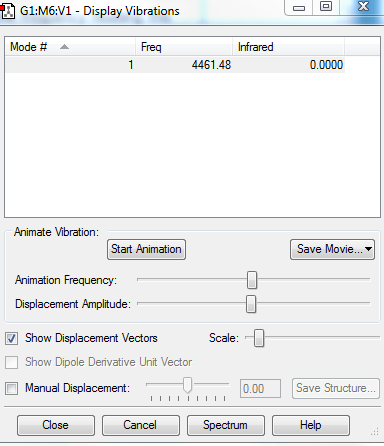
Vibrational Analysis
1.How many modes do you expect from the 3N-5 rule?
3(2)-5 = 1 mode
2.Which modes are "bending" vibrations and which are "bond stretch" vibrations?
1: bond stretch as the bond lengths change
3.How many bands would you expect to see in an experimental spectrum of gaseous Fluorine?
There is a vibration at 1063.53cm-1 but this will not result in a band in an experimental spectrum as the molecule is IR inactive because it has no change in dipole due to the symmetry.
Charge Analysis
Charge on F atoms=0
Energy of F2
-199.49825212 a.u. = -125187.10 kJ/mol
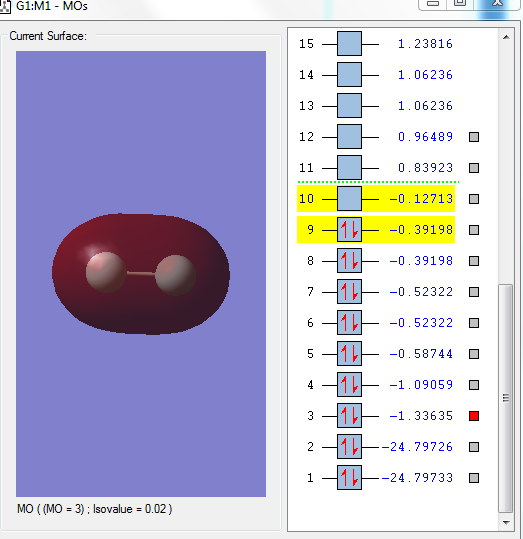
Molecular Orbitals
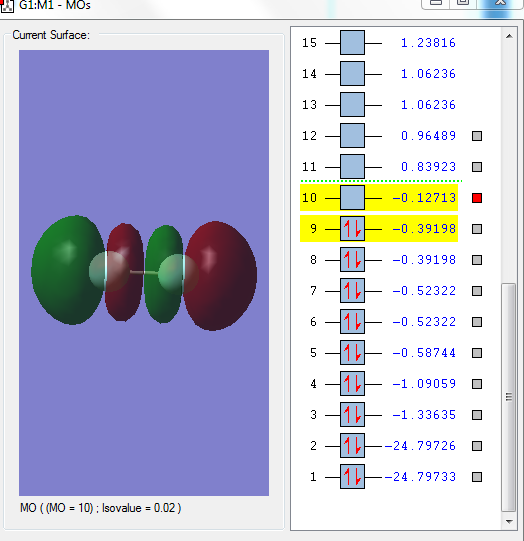
Image 1: LUMO
The above orbital is the LUMO and it is the 3σ*u. It has the highest orbital energy as it has the most number of nodes. F2 accepts electrons in this orbital.
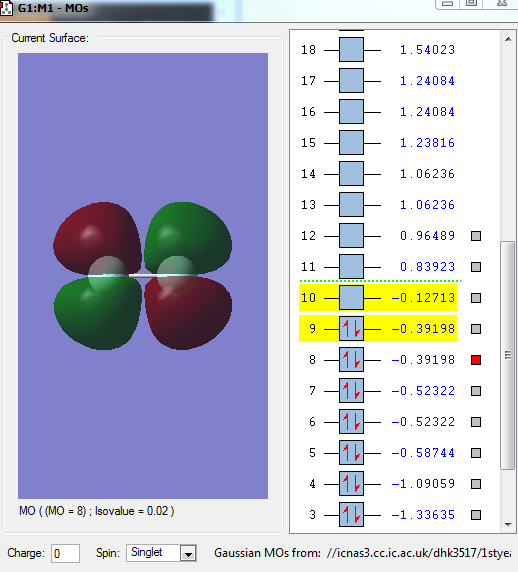
Image 2: HOMO
The HOMO of F2 is the 1π*g. Electrons are donated from this orbital.
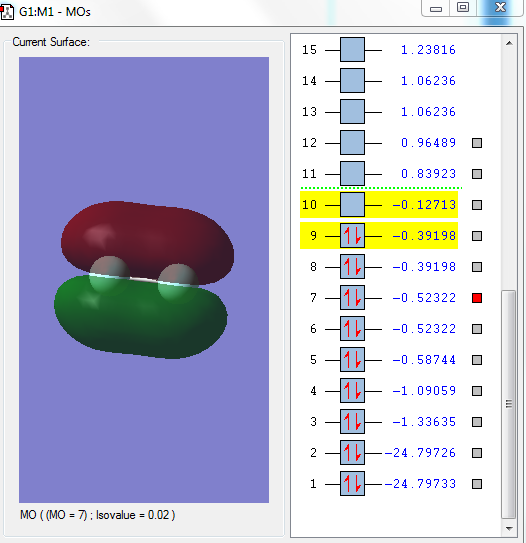
Image 3
This is the bonding orbital, 1πu of pz orbitals from each F. Px and py are non-bonding orbitals due to the incorrect geometry.
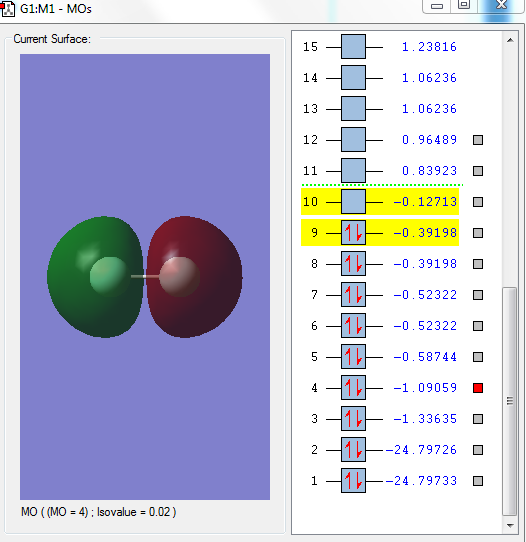
Image 4
This is the filled sigma anti-bonding orbital, 2σ*g. The two 2s orbitals from each F contribute to this orbital.
Image 5
This is the sigma bonding orbital, 2σg. The two 2s atomic orbitals from each F atom contributes to this orbital. There is no mixing between the 2s and 2p orbitals of F as they are too different in energy.