Rep:MOD:cc5115
Ammonia
Optimized NH3 Molecule
N-H bond distance = 1.01798
H-N-H bond angle = 105.741
Summary
Molecule = NH3
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p) Final Energy ERB3LYP = -56.55776873 a.u.
RMS Gradient = 0.00000485 a.u.
Point Group = C3v
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986276D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is linked to here
Ammonia |
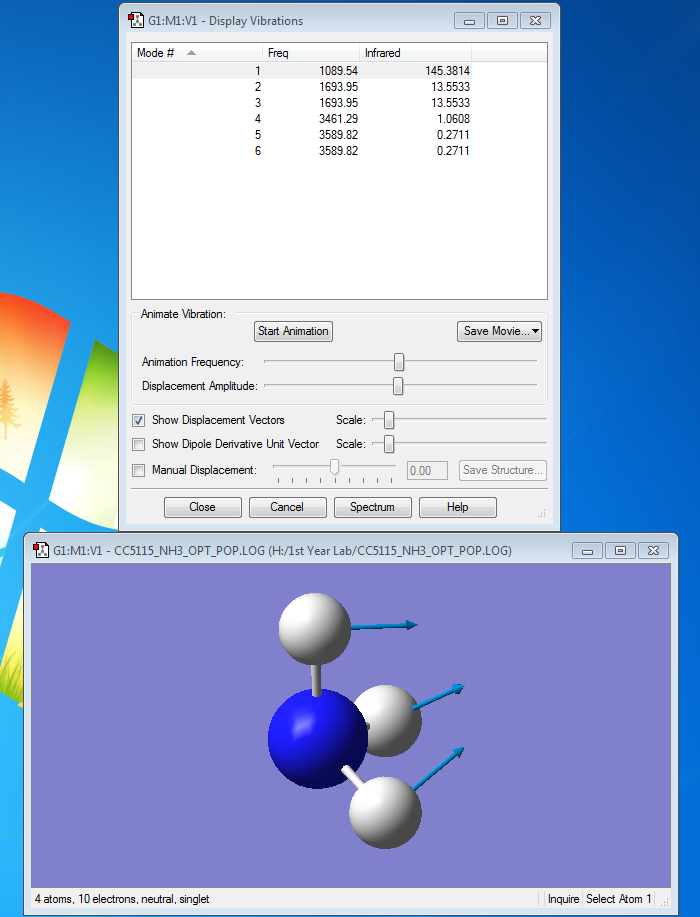
How many modes do you expect from the 3N-6 rule?
Ans: 6
Which modes are degenerate (ie have the same energy)?
Ans: 2 and 3, 5 and 6
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Ans: Bending vibration modes are 1,2 and 3. Bond stretch vibration modes are 4,5 and 6.
Which mode is highly symmetric?
Ans: 4
One mode is known as the "umbrella" mode, which one is this?
Ans: 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
Ans: 2. There are only 2 visible peaks in the IR spectrum. This is because the intensities for mode 4,5 and 6 are too small to be of significance. The reason that their intensities are small is because that there isn't a big change in dipole moment.
Charge Distribution of Ammonia
N = -1.125
H = 0.375
It is expected that the Nitrogen atom has a negative charge because it is more electronegative than the Hydrogen atom.
Haber-Bosch Process
N2 + 3H2 → 2NH3
N2 Summary
Molecule = N2
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Final Energy ERB3LYP = -109.52412868 a.u.
RMS Gradient = 0.00000060
Point Group = D*H
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401007D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Nitrogen |
The optimisation file is linked to here
List Of Frequency- Display Vibrations
| Mode | Freq | Infrared |
|---|---|---|
| 1 | 2457.33 | 0.0000 |
It is expected that there is only one peak in the IR spectrum because there is only one vibrational mode for this diatomic molecule.
Charge Distribution of Nitrogen
N = 0
Charge is zero because it is a diatomic molecule and thus non-polar.
H2 Summary
Molecule = H2
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Final Energy ERB3LYP = -1.17853936 a.u.
RMS Gradient = 0.00000017 a.u.
Point Group = D*H
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Hydrogen |
The optimisation file is linked to here
List Of Frequency- Display Vibrations
| Mode | Freq | Infrared |
|---|---|---|
| 1 | 4465.68 | 0.0000 |
It is expected that there is only one peak in the IR spectrum because there is only one vibrational mode for this diatomic molecule.
Charge Distribution of Hydrogen
H = 0
Charge is zero because it is a diatomic molecule and thus non-polar.
Energy for the Haber-Bosch reaction
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579070 a.u
ΔE= -146.48 kJ mol-1. Therefore, the ammonia product is more stable than the gaseous reactants.
Chlorine
Summary
Molecule = Cl2
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Final Energy ERB3LYP = -920.34987886 a.u.
RMS Gradient = 0.00002511 a.u.
Point Group = D*H
Item Value Threshold Converged?
Maximum Force 0.000043 0.000450 YES
RMS Force 0.000043 0.000300 YES
Maximum Displacement 0.000121 0.001800 YES
RMS Displacement 0.000172 0.001200 YES
Predicted change in Energy=-5.277362D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.0417 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is linked to here
Chlorine |
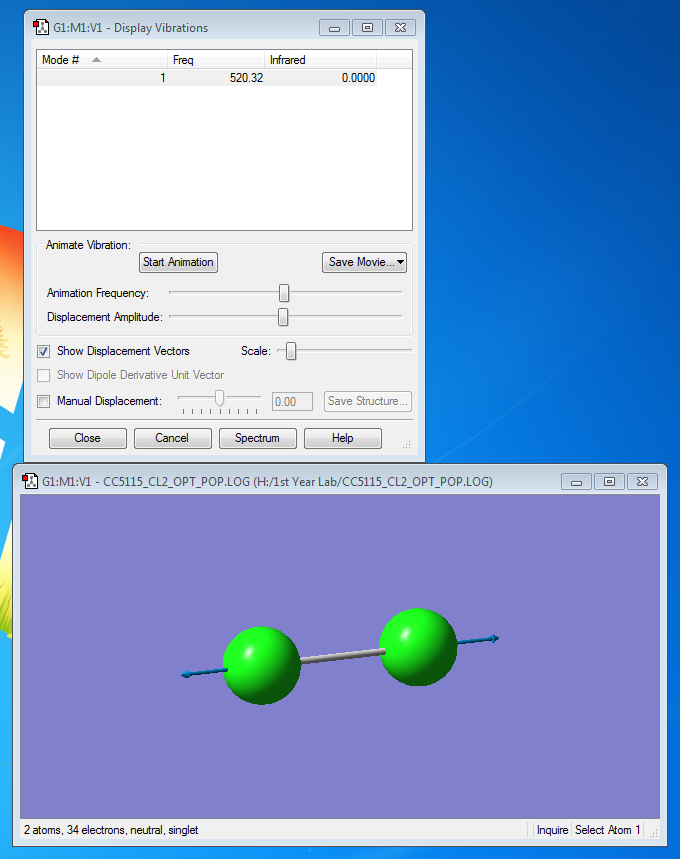
List Of Frequency- Display Vibrations
| Mode | Freq | Infrared |
|---|---|---|
| 1 | 520.32 | 0.0000 |
It is expected that there is only one peak in the IR spectrum because there is only one vibrational mode for this diatomic molecule.
Charge Distribution of Chlorine
Cl = 0
Charge is zero because it is a diatomic molecule and thus non-polar.
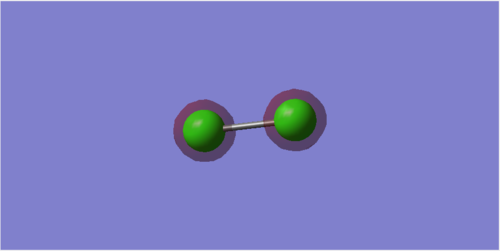
Molecular Orbitals
1s anti-bonding orbital
The energy for this orbital is -101.60298 a.u. which is extremely low. The two atomic orbitals doesn't overlap and doesn't involve in any chemical bonding.
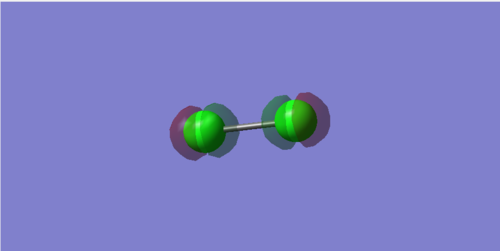
2s bonding orbital
The energy for this orbital is -9.51828 a.u., which is still too low to form bonds with other orbitals and thus does not involve in any chemical bonding.
2p anti-bonding orbital
The energy for this orbital is -7.28592 a.u., which is still too low to form bonds with other orbitals and thus does not involve in any chemical bonding. There are 3 p orbitals which are degenerate and they can orient in 3 different directions: along the x axis, y axis or the z axis.
2p bonding orbital
The energy for this orbital is -7.28592 a.u. and is degenerate to the above 2p anti-bonding orbital. The energy is too low to form bonds with other orbitals and thus does not involve in any chemical bonding.
3s bonding orbital
The energy for this orbital is -0.93313 a.u. which is a much higher value compared to the energies of the molecular orbitals shown above and thus can be involved in chemical bonding.