Rep:MOD:ZLY0512
Transition states and reactivity
Introduction
In a potential energy surface, the transition state is where it has a maximum amount of energy. The gradient of the transition state is zero. Since it is a maximum, the second derivative/curvature of the transition state is negative. For a molecule at its transition state, the energy decreases in the direction of the reaction path. In the frequency calculation, a imaginary frequency confirms that the structure is at the transition state as a negative energy give a negative force constant and hence the square root of a negative force constant gives an imaginary frequency.
On the contrary, a minimum in the potential energy surface shows that the structure of a molecule is stable. The gradient again is equal to zero and the curvature is positive.
In this experiment, GaussView is used to analyse three reactions. The semi-empirical method PM6 and the Density Functional Theory (DFT) method B3LYP were mainly used. In the experiment, PM6 is used to generate initial geometries and then optimised with B3LYP. From the energy of the transition state of each reaction, we can find out which path of the reaction is more favourable.
Nf710 (talk) 16:47, 4 November 2016 (UTC) Good understanding
Exercise 1: Reaction of Butadiene with Ethylene
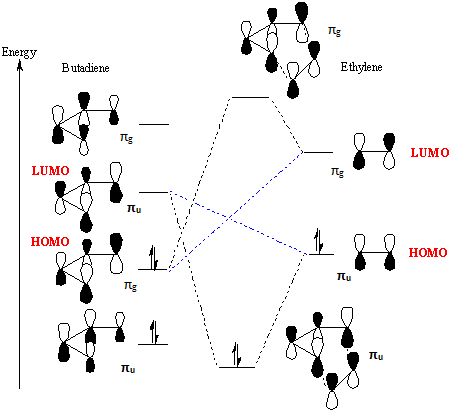
Figure 1: MO diagram of Diels-Alder reaction between diene and dienophile.[1]
For the Diels-Alder reaction, the best interaction of the diene and the dienophile is between the HOMO of the diene and the LUMO of the dienophile.
For a reaction that is allowed, the interacting orbitals need to have the same symmetry. In this particular reaction, the symmetry of the two interacting MOs are ungerade.
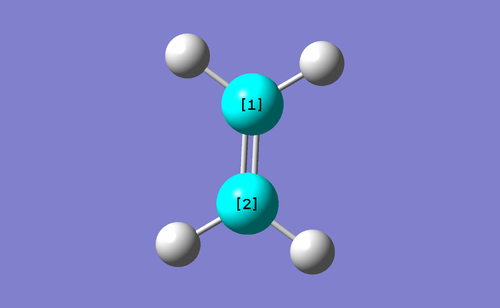
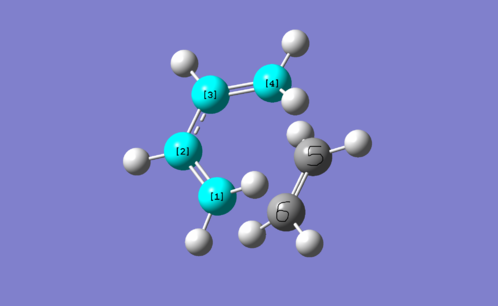
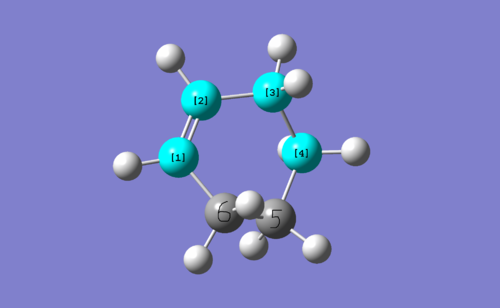
HOMO-LUMO MOs of ethene, butadiene and TS.
| HOMO | LUMO | |
|---|---|---|
| Ethene | 
ungerade |
 |
| Butadiene |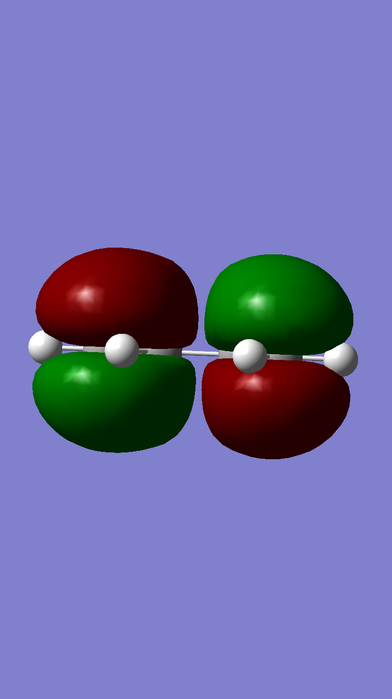 
gerade |
ungerade |
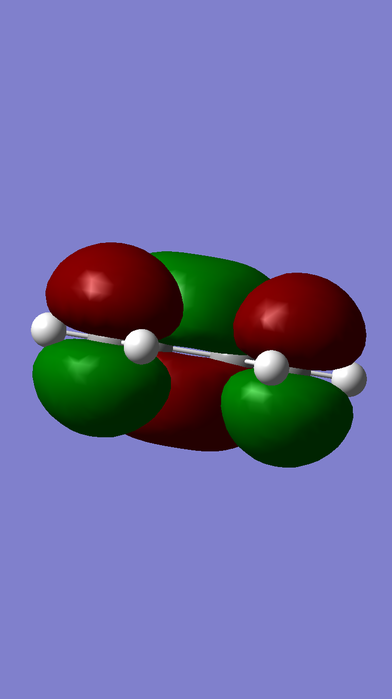
| TS |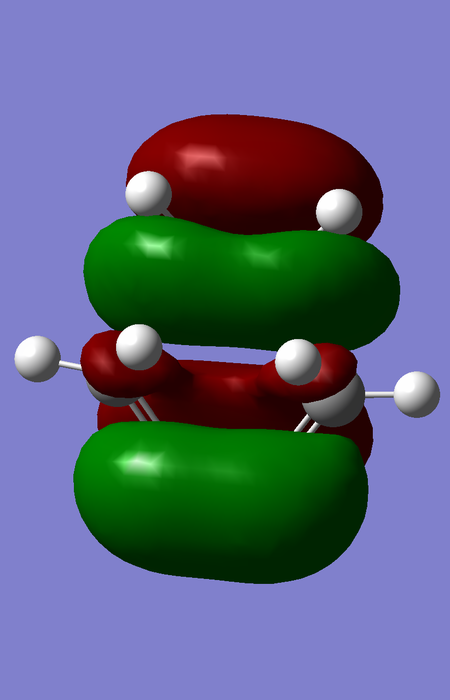 
|
|
The orbital overlap integral is zero for a gerade-ungerade interaction, non-zero for a gerade-gerade interaction and non-zero for an ungerade-ungerade interaction.
Carbon-carbon distance in the reactants, TS and product.
| Bond distance (Å) | ||
|---|---|---|
| Ethene | 
|
(C1)-(C2): 1.32731 |
| Butadiene | 
|
(C1)-(C2): 1.33519
(C2)-(C3): 1.46837 (C3)-(C4): 1.33519 |
| TS | 
|
Butadiene:
(C1)-(C2): 1.37981 (C2)-(C3): 1.41111 (C3)-(C4): 1.37970 Ethene: (C5)-(C6) distance: 1.38173 Intermolecular: (C6)-(C1): 2.11391 (C4)-(C5): 2.11519 |
| Product | 
|
(C6)-(C1): 1.50034
(C1)-(C2): 1.33766 (C2)-(C3): 1.50034 (C3)-(C4): 1.54003 (C4)-(C5): 1.54076 (C5)-(C6): 1.54003 |
The typical sp3 and sp2 C-C bond lengths are 1.544 Å and 1.334 Å respectively. The Van der Waals radius of the C atom is 1.70 Å.[2]
Compare the literature values with the length of the partly formed C-C bonds in the TS, we can see that the single bonds in the TS are shorter and the double bonds in the TS are longer.
This indicates the resonance of electron density across all the carbon-carbon bonds in the transition state.
Furthermore, the intermolecular distances between butadiene and ethene are shorter than two times of the Van der Waals radius of the C atom, which tells that the during the reaction carbon-carbon single bonds are formed.
The vibration that corresponds to the reaction path at the transition state:
| Imaginary frequency | Lowest positive frequency | |
|---|---|---|
|
|
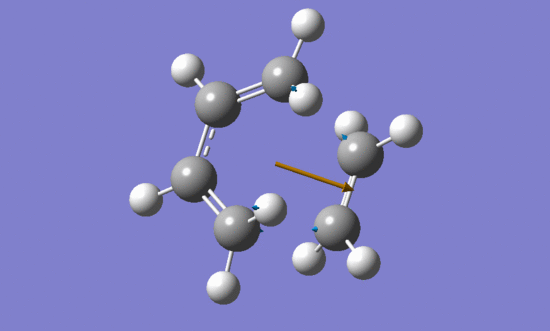
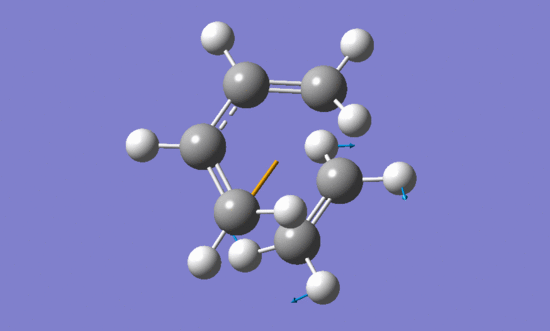
The formation of the two bonds is synchronous.
According to the vibrations of two reactants in the lowest positive frequency they can not form bonds between each other.
Nf710 (talk) 16:58, 4 November 2016 (UTC) You could have just shown this in an animation. A better explanation of why the imaginary frequency shows the reaction would be better.
Exercise 2: Reaction of Benzoquinone with Cyclopentadiene
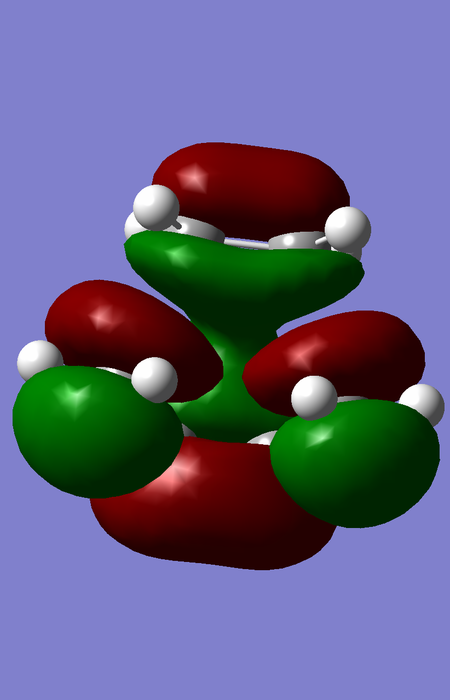
HOMO-LUMO MOs of Cyclopentadiene, Benzoquinone and both endo-exo products.
| HOMO | LUMO | |
|---|---|---|
| Cyclopentadiene | 
|
|
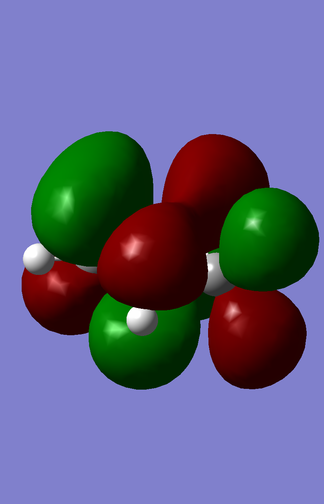
| Benzoquinone |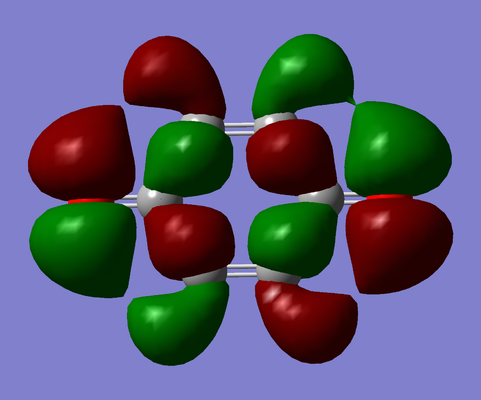 
|
|
| Endo-product |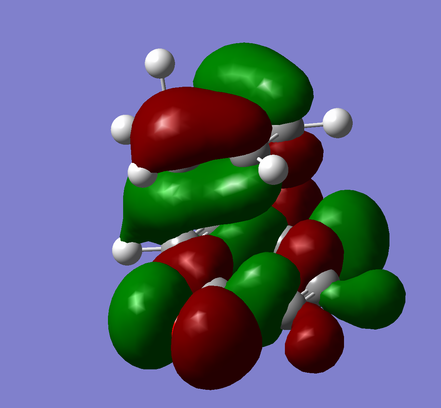 
|
|
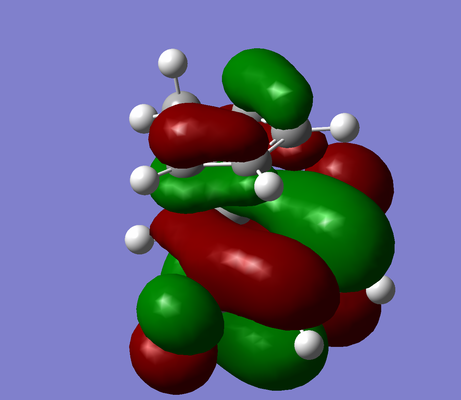
| Exo-product |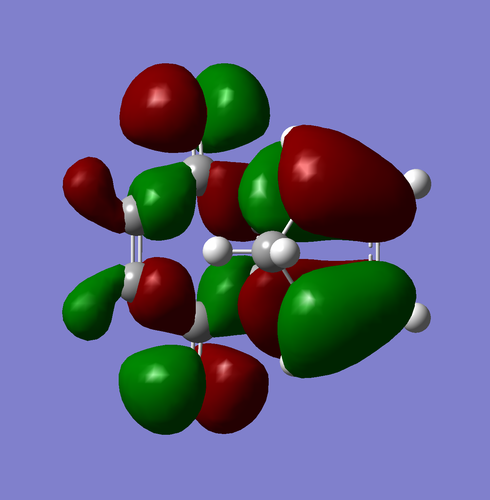 
|
|
From the MOs of both endo and exo product, we can conclude that this reaction has a normal demand for DA reaction. This can be rationalized by the fact that C=O is an EWG that contains on the dienophile. An EWG on the dienophile tends to lower its LUMO and hence led to a better interaction with the diene HOMO.
Sum of electronic and thermal energies in the reaction of benzoquinone and cyclopentadiene.
| Sum of electronic and thermal free energies/ Hartrees per partical | |
|---|---|
| Cyclopentadiene | -194.034781 |
| Benzoquinone | -381.396831 |
| endo-TS | -575.381306 |
| Exo-TS | -575.383854 |
| Endo-product | -575.385423 |
| Exo-product | -575.382028 |
| Activation energy / Hartrees | reaction energy / Hartrees | |
|---|---|---|
| Endo | 0.045210 | 0.046189 |
| Exo | 0.047758 | 0.042794 |
Since Endo-transition state has a lower energy, which means the activation energy is less, endo-form is the kinetic product.
Exo-product has a lower energy, hence exo-product is the thermodynamic product.
Base on the HOMOs of both endo and exo transition states, there are some secondary orbital interactions in the endo TS, which gives rise to a decrease in the activation energy. However, the endo arrangement becomes more steric hindered and might increase the activation barrier. Overall, the orbital contribution outweighs the steric effect and hence makes the reaction faster.
Nf710 (talk) 17:23, 4 November 2016 (UTC) You have shown with your data that the endo is both the kenetic and thermodynamic product. but have contradicted yourself. Your TS energies are correct
Exercise 3: Diels-Alder vs Cheletropic
Reaction animations and IRCs of Diels-Alder and cheletropic reactions in the o-Xylylene-SO2 cycloaddition.
| Reaction Animation | IRC | |
|---|---|---|
| Diels-Alder
Endo |
|
|
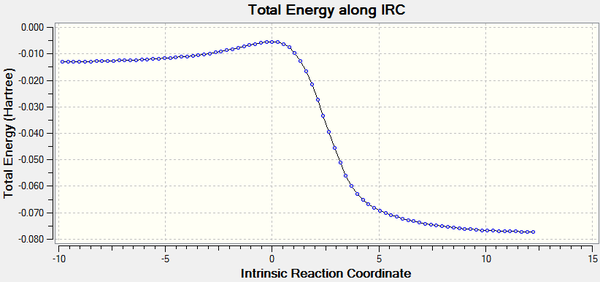
| Diels-Alder
Exo |
|
|
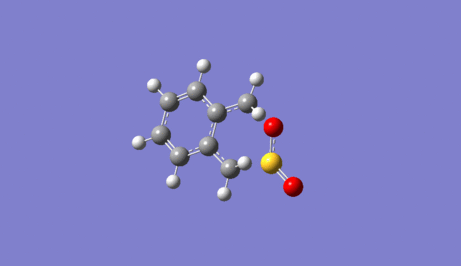
| Cheletropic | 
|
|
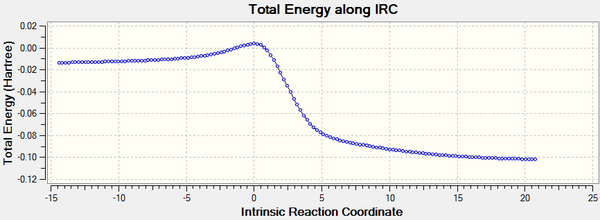
Energies of the reactants, TSs and products in the o-xylylene-SO2 cycloaddition.
| Xylylene | SO2 | Endo-DA-TS | Exo-DA-TS | Cheletropic-TS | Endo-DA-product | Exo-DA-product | Cheletropic-product | |
|---|---|---|---|---|---|---|---|---|
| Zero-point correction /Hartrees per partical | 0.124079 | 0.005699 | 0.131998 | 0.131899 | 0.131558 | 0.135511 | 0.132064 | 0.136199 |
| Thermal correction to Energy /Hartrees per partical | 0.131218 | 0.009105 | 0.142191 | 0.142126 | 0.141999 | 0.145011 | 0.142523 | 0.145229 |
| Sum of electronic and thermal Free Energies / Hartrees per partical | 0.177651 | -0.118614 | 0.090561 | 0.092079 | 0.099060 | 0.021706 | 0.021455 | 0.000005 |
(Convert energies to kJ/mol Tam10 (talk) 13:47, 31 October 2016 (UTC))
Activation energies of the endo-exo Diels-Alder reaction and the Cheletropic reaction in the o-xylylene-SO2 cycloaddtion.
| Endo-DA | Exo-DA | Cheletropic | |
|---|---|---|---|
| Activation energy/ Hartrees per partical | 0.031524 | 0.033042 | 0.040023 |
| Reaction energy/ Hartrees per partical | -0.037331 | -0.037582 | -0.0590320 |
Energy profile of the o-xylylene-SO2 cycloaddition
As predicted, in the Diels-Alder reaction the endo form which is the kinetic product has a lower activation energy than the exo form which is the thermodynamic product. The Cheletropic reaction has a higher activation energy than the Diels-Alder reaction.
Compare the product energies for three paths, the cheletropic product has a lower energy than both of the endo-exo product. Again as predicted, the thermodynamic exo product has a lower energy than the kinetic endo product.
Overall, we can conclude that under thermodynamic condition, the cheletropic reaction will dominate. Under kinetic control, the Diels-Alder reaction, in particular the endo product will dominate.
Xylylene is not aromatic since the molecule does not satisfy the Huckel's Rule. Xylylene is highly unstable therefore during the reaction, the 6-membered ring tries to gain its aromaticity first (TS lower in energy) then forms bonds with SO2.
Conclusion
This experiment allows us to use GaussView to analyse the reaction by modifying its arrangement in the transition state and hence find the path with the lowest energy.
In the exercise one, a simple Diels-Alder reaction was analysed by the software and rationalized by the MO theory. The best interaction involves the HOMO of the diene and the LUMO of the dienophile. From the MOs obtained by Gaussview the basic rule of the MO theory is revealed, which is that only the orbitals with the same symmetry can combine.
In the exercise two, both exo and endo forms of the Diels-Alder reaction were discovered. By calculating the transition state energies and the product energies, the kinetic product and the thermodynamic product were found to be corresponded to the endo and exo respectively.
In the exercise three, once again the cycloaddition reaction was investigated. The reaction between xylylene and sulfur dioxide has two main paths. One is Diels-Alder, including the exo and endo forms, and the other one is Cheletropic. The energies for each reaction were calculated by the TSs of each reaction. From the data the activation energy for each path was calculated and used to find the best route of this reaction under either kinetic or thermodynamic condition which is the Diels-Alder and the Cheletropic reaction respectively.
References
- ↑ Boger, Dale (1989). Progress in heterocyclic chemistry (1st ed.). New York: Pergamon. ISBN 978-0-08-037044-6.
- ↑ Pauling, L. (1931). THE NATURE OF THE CHEMICAL BOND. II. THE ONE-ELECTRON BOND AND THE THREE-ELECTRON BOND. J. Am. Chem. Soc., 53(9), pp.3225-3237. doi:http://pubs.acs.org/doi/abs/10.1021/ja01360a004