Rep:MOD:Yz19114

Y3C-Computational lab Transition states and reactivity

Introduction

In this computational lab session, the aim is to locate and characterise transition states of several pericyclic reaction by applying suitable methods in GaussView. Firstly several basic concepts need to be explained. A potential energy surface is a mathematical function that gives the energy of a molecule as a function of its geometry, a minimum in PES is a point at which the energy rises in all directions, and a transition state is a point at which the energy decreases along the reaction pathway. The gradients (first derivatives) of these two points are all zero but the curvature(second derivative) of a minimum is positive and the curvature of a transition state is negative because the energy is maximum at TS along the reaction pathway. And the frequency is equal to the second derivative, so a negative frequency corresponds to a transition state.

Nf710 (talk) 17:25, 4 November 2016 (UTC) Imaginary frequency, Gaussian just prints it as a negative.

Exercise 1: Reaction of Butadiene with Ethylene

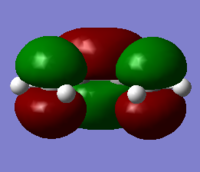
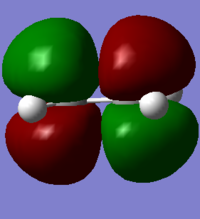
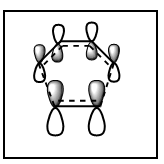
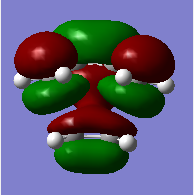
MO diagram for the formation of the butadiene/ethene TS(normal demand DA)

	HOMO	LUMO
Butadiene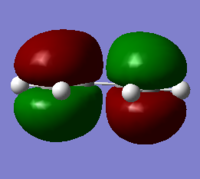
Ethene
Transiotion State

From the HOMO and LUMO diagrams above, it can be seen that the HOMO of ethene interacts with the LUMO of butadiene to give the HOMO(in-phase) and LUMO(out-of-phase) of transtion state. And it is obviously that all these orbitals are gerade, so the symmetry of two interacted orbitals should be the same when the reaction is allowed, otherwise the reaction is forbidden. The orbital overlap integral is zero for the case of a gerade-ungerade interaction and non-zero for the case of a gerade-gerade interaction and an ungerade-ungerade interaction.

	Butadiene	Ethene	Transition State	Product(cyclohexene)
Bond length ( ‎Å)	C12=C34=1.335 C23=1.468	1.327	C12=C34=1.380 C23=1.411 C56=1.382 C16=C45=2.115	C12=C34=1.501 C23=1.338 C56=1.541 C16=C45=1.540

As reaction proresses, C12 and C34 bond lengths increases because the double bonds in butadiene breaks gradually to form single bonds, the same reason for C56 double bond in ethene. And C23 bond length decreases as a new double bonds forms gradually. Typical sp3 and sp2 C-C bond lengths are 1.54Å and 1.34‎Å respectively, and the Van der Waals radius of the C atom is 1.7Å.[1][2] Van der Waals radius is used to define half of the distance between the closest approach of two non-bonded atoms of a given element.[3] Partly formed C-C single bond length (C16 or C45) is 2.115 Å, which is shorter than double Van der Waals radius(3.4Å).

TS Vibration	Lowest Positive Frequency Vibration	IRC Animation	IRC plots

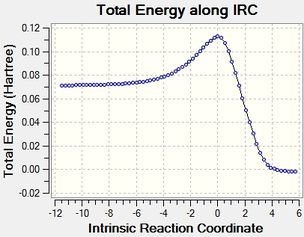
According to the transition state vibration diagram, it seems like the two reactants vibrate towards each other to form new C-C bonds. The IRC can prove that two new C-C single bonds formed simultaneously, and there is only one peak in the IRC plots which shows two bond are formed synchronously as well. While in the lowest positive frequency vibration diagram, the two reactants vibrate parallel to each other, which shows they are not going to react with each other and it is not the same as a TS.

Nf710 (talk) 17:37, 4 November 2016 (UTC) Good use of IRC to show that bond formation is synchronous. More detail about why this coordinate can be used to show bond formation would have been good.

Exercise 2: Reaction of Benzoquinone with Cyclopentadiene

	HOMO	LUMO
Cyclopentadiene
Benzoquinone
Endo TS
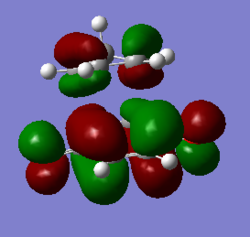
Exo TS

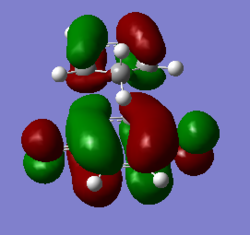
According to the MO diagrams, it can be seen that HOMO of dienophile(benzoquinone) interacts with LUMO of diene (cyclopentadiene) to give MOs of transition state, so it is a normal demand DA reaction. And the reason is that double bond in benzoquinone is relatively electron-rich due to the C=O electron-donating group, so the HOMO of benzoquinone has relatively high energy, which prefers to interact with LUMO of cyclopentadiene.

	Sum of electronic and thermal Free Energies(KJ/mol)
Cyclopentadiene	-194.0348
Benzoquinone	-381.3968
Total Energy of reactants	-575.4316
Endo TS	-575.3839
Endo Product	-575.4173
Endo Activation Enery	0.0477
Endo Reaction Energy	0.0143
Exo TS	-575.3813
Exo Product	-575.4261
Exo Activation Energy	0.0503
Exo Reaction Enegy	0.0055

According to the table above, the exo product has a lower energy(-575.4261) compared with endo product(-575.4173), and the reaction energy for exo product is smaller than that for endo product as well. So the exo product is thermodynamically favourable. And the activation energy for endo product (0.0477) is smaller that for exo product(0.0503), so the endo product is kinetically favourable. Furthermore, the HOMO of endo product indicates there is secondary orbital interactions which lower the energy of TS and the activation energy as well, but there is more steric hindrance in endo TS which increases energy. Overall, the secondary orbital interactions contribute more to lower the activation energy to make endo product more kinetically favourable.

Nf710 (talk) 17:49, 4 November 2016 (UTC) Your TS energies are correct and your have presented a well balanced argument. However the energy of your endo product is wrong and therefore you havent got the correct conclusion that it is both. Very well written section.

Exercise 3: Diels-Alder vs Cheletropic

	IRC Animation	IRC Plots
Diels-Alder endo product
Diels-Alder exo product
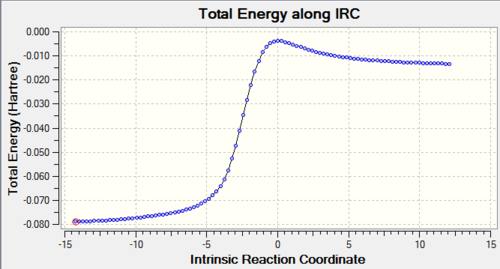
Cheletropic product

	o-xylylene	Sulfur Dioxide	sum of two reactants	DA endo TS	DA exo TS	Chel TS	DA endo product	DA exo product	Chel product
Thermal Correction(Hartrees)	0.1312	0.0091	0.1403	0.1422	0.1421	0.1420	0.1450	0.1450	0.1452
Zero Point Correction(Hartrees)	0.1241	0.0057	0.1298	0.1320	0.1319	0.1316	0.1355	0.1356	0.1362
Sum of electronic and thermal free energies(Hartrees)	0.177945	-0.118614	0.059331	0.090560	0.092077	0.099062	0.021706	0.021455	0.000002

	DA endo	DA exo	Chel
Activation Energies(Hartrees)	0.031229	0.032746	0.039731
Reaction Energies(Hartrees)	-0.037625	-0.037876	-0.059329

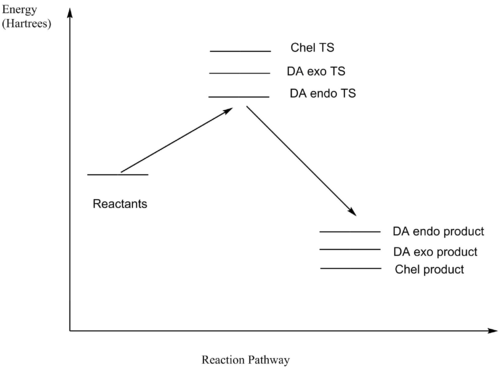
According to the data and reaction profile above, the activation energy of Cheletropic reaction is the highest, but the reaction energies of two DA reactions are higher than that of Cheletropic reaction. So under high temperature, there is sufficient energy to overcome the energy barrier, DA route is preferred because the product is thermodynamically favourable. However, under low temperature, Cheletropic route is preferred because kinetic product is preferred.

According to the IRC animations, it can be seen that a new double bond is formed in the six-membered ring to give a stable arometic benzene ring and the electrons in the six-membered ring becomes delocalised. So the overall reaction is exothermic due to the stabilisation of pi delocalised system in benzene ring.

Conclusion

In this computational lab, firstly we learned three methods of optimising minima and transition state in GaussView to locate and characterise transition structures of several pericyclic reactions, and we can decide if the DA reaction is a normal or reverse demand by comparing MOs of transition state with MOs of reactants. Furthermore, we can calculate the energy barriers and reaction energies by frequency calculations on reactants, transition states and products to judge if the reaction is thermodynamically or kinetically favourable. Besides, we can analysis the HOMO of the transition state to judge whether there is a secondary orbital interactions or steric hindrance or not. And also we can decide if the formation of bonds is synchronous or asynchronous by looking at the IRC animation.

Reference

[1]: Lide, David R. "A survey of carbon-carbon bond lengths." Tetrahedron 17.3 (1962): 125-134.

[2]: Batsanov, S. S. "Van der Waals Radii of Elements." Inorganic Materials 37.9 (2001): 871-885.

[3]:http://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Chemical_Bonding/General_Principles_of_Chemical_Bonding/Covalent_Bond_Distance,_Radius_and_van_der_Waals_Radius