Rep:MOD:Yw10612

Introduction

This experiment was aiming to study the transition states involved in the reaction pathway of pericyclic reactions. Two types of pericyclic reactions, the [3,3]-cope rearrangement and the Diels-Alder cycloaddition were optimized and calculated. The boat and chair transition structures involved in the [3,3]-cope rearrangement of 1,5-cyclohexadiene were optimized and the geometries and the activation energies of each were compared. The cycloaddition of cis-butadiene with ethylene, and the cycloaddition of maleic anhydride with 1,3-hexadiene were studied by optimizing the transition structures. The optimization was carried out by GaussView 5.0 using different methods under different energy levels, typically HF/3-21 G and B3LYP/6-31 G*. The endo transition state and exo transition state were compared and the calculation results were used to discuss the reaction mechanisms.

Methods

Hartree–Fock (HF) method

The Hatree-Fock (HF) method was discovered in 1920s. It is a starting point of studying the energy and wave function of a many-electron system based on the Born–Oppenheimer approximation. A single slater determinant is used to approxiamte the whole N-electron wave function, as a product of one-electron wave functions. By using variational solution, the Fock operators are obtained and used to solve the wave function by optimizing the orbitals to meet the threshold value of the total electronic energy. The variational method is approximated as a linear combination of basis sets and the electron-electron correlation is not accounted in this method.

Semi-empirical

Semi-empirical is a quantum method founded on the Hartree-Fock formalism. It is used to fit the results from the HF solution by setting appropriate parameters, and make the results meet the experimental results as close as possible. The calculations are fast owing to the assumption of differential overlap as zero.

Density functional theory (DFT)

The DFT method involved the determination of energy of the many-electron system in terms of functionals such as electron density. The convergence is attempted to be obtained from the predicted electron density via Koh-Sham equation. Compared to HF method, DFT method involved the consideration of both electron-electron correlation and electron-electron exchange. However, as the functionals for the correlation are difficult to determine exactly, a local-density approximation is required for calculations.It assumed that the functionals are only determined by the density at the particular position.

Semi-empirical method

Semi-empirical quantum chemistry method is a calculation based on HF formalism with appropriate parameters to correct the loss caused by HF approximations. In this way, it can be used to study large molecules without using expensive HF method.The semi-empirical method is limited by the zero differential overlap approximation therefore the structure of molecule should be created in an appropriate geometry for reliable results. In this experiment, AM1 with the Neglect of Differential Diatmoic Overlap approximation was chosen.

Basis sets

The basis set is a linear combination of basis functions, such as atomic orbitals, aiming to construct the molecular orbitals, The atomic orbitals are expressed by slater type orbitals and to simplify the calculations of Gaussian functions, the slater type orbitals are assumed as a linear combination set of Gaussian orbitals. Two types of basis sets, 3-21 G and 6-31 G* are used in this experiment.

The Cope Rearrangement of 1,5-hexadiene

The [3,3]-sigmatropic rearrangement of 1,5-hexadiene is a class of pericyclic reaction. It occurs via a mechanism with simultaneous sigma bond formation an a sigma bond broken. The reaction is shown below.

Optimization of the Reactants and Product

Principally, 1,5-hexadiene has 27 conformations as it has three free-rotating carbon carbon single bond. But in fact it has only six gauche conformations and four anti-periplanar conformations due to the symmetry. In the gauche conformation, the dihedral angle is 60° while in the anti conformation, the dihedral angle is 180°. Therefore the substituents attached to carbon would suffer steric clashing in the gauche conformation. In this experment, the conformers of were 1,5-hexadiene crated, cleaned and optimized by using Gauss View 5.0. The HF method with basis set 3-21 G was chosen for optimization and the results including structures, point group and energy are expressed below. The results are correlated with the data given in the of experimental script. It was expected to see the lower energy of anti-periplanar conformations compared to gauche conformations, due to the steric clashing in gauche conformers. However, it is clearly shown from the table that the conformer gauche 3 adopts the lowest energy. It is because the energy of gauche 3 conformer adopts the overlap of pi-orbital of the double bond with the vinyl hydrogen of the other double bond and hence lowering of energy is achieved.

Conformor	Structure	Calculation Summary	Point Group	Energy/hartrees
Gauche 1		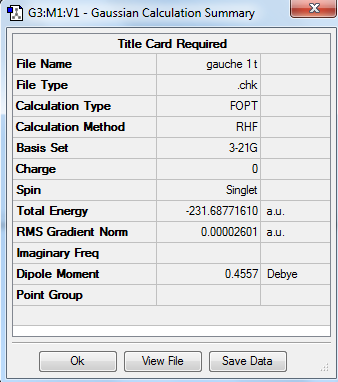	C2	-231.687716
Gauche 2		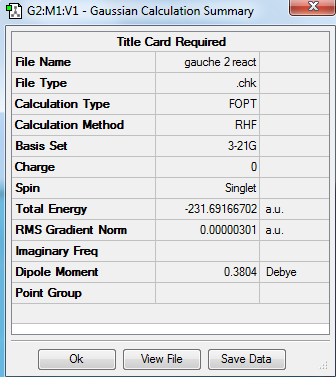	C2	-231.691667
Gauche 3		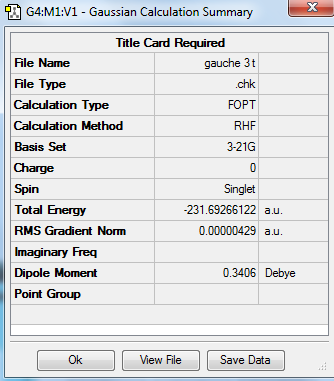	C1	-231.692661
Gauche 4		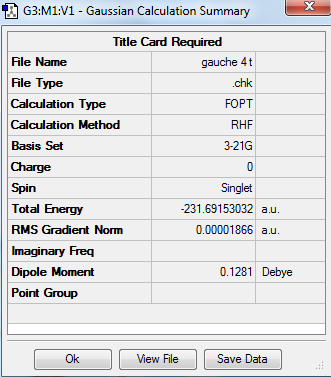	C2	-231.691530
Gauche 5		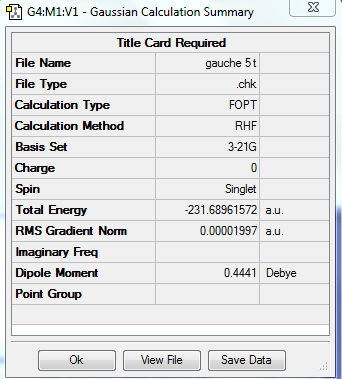	C1	-231.689615
Gauche 6		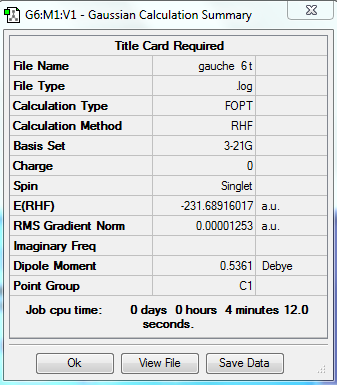	C1	-231.689160
Anti 1		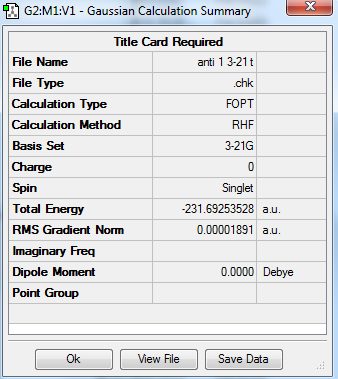	C2	-231.692602
Anti 2			Ci	-231.692535
Anti 3		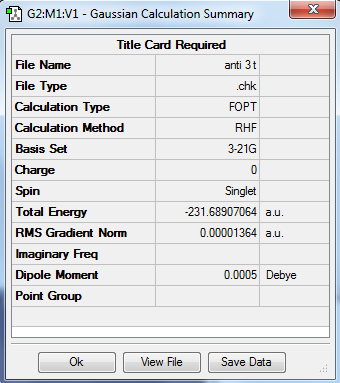	C2h	-231.689070
Anti 4		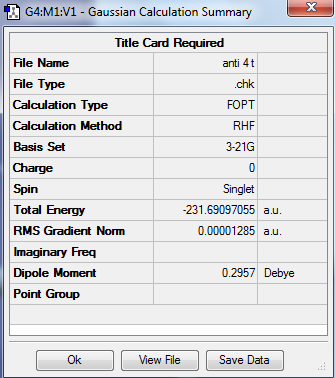	C1	-231.690971

The anti 2 conformation was further optimized by carrying out B3LYP with 6-31 G* basis set. The results are shown in the table below. As the optimization of conformers by using B3LYP/6-31 G* was at a higher energy level calculation than HF/3-21 G, therefore the geometry comparison of two resulted anti 2 structures was made instead of energy comparison. The bond lengths of C-C bond and dihedral angles are compared and shown in the table below. It is clearly shown that the difference of bond lengths of the structures optimized from two methods are very small, but the dihedral angles of C1-C2-C3-C4 and C2-C3-C4-C5 increased from HF/3-21 Gto B3LYP/6-31 G*. As the predicted angles of C1-C2-C3-C4 and C2-C3-C4-C5 were 120° and 180° respectively, the dihedral angles of the structure calculated from B3LYP/6-31 G* were closer to the predicted values. The larger dihedral angles in B3LYP/6-31 G* illustrated that the C₁ and C₆ atoms are now further away from each other. The differences in dihedral angles and bond lengths was caused by the consideration of electron-electron interaction in the DFT method. Therefore calculation under B3LYP/6-31 G* level would give more reliable result than HF/3-21 G.

Optimization of anti 2 conformer using B3LYP/6-31 G*
Conformer	Structure	JSmol	Point group	Energy/hartrees
Anti 2			Ci	-234.626831

The comparison of anti 2 conformations by using to methods
Method	Bond length C1-C2/Å	Bond length C2-C3/Å	Bond length C3-C4/Å	Dihedral Angle of C1-C2-C3-C4/°	Dihedral Angle of C2-C3-C4-C5/°
HF/3-21 G	1.31613	1.50886	1.55291	114.66262	179.99802
B3LYP/6-31 G*	1.33349	1.50420	1.54844	118.58131	180.00000

The anti 2 conformer optimized from B3LYP/6-31 G* was further studied by frequency calculation under the same energy level. The results confirmed that there are no imaginary frequency present. The frequency is calculated as the product of 1/2πc and square root of eigenvalue (converted from Hessian), and the Hessian is defined as a secondary derivative of energy with respect to the coordinates i and j. Therefore a negative value of frequency means a negative secondary derivative of energy and hence means the maximum value of energy. As a result, the built up of minimum energy conformation of anti 2 is confirmed by frequency calculation.

Calculation Summary

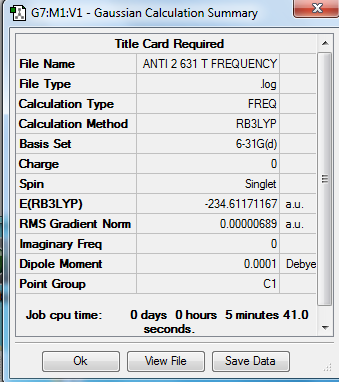
By reading from the Thermochemistry data in the output file, the different types of energies at 0 K and 298.15 K were obtained and illustrated in the table below. The frequency calculation could be operated at 0 K and higher temperatures for comparison.

Energy Type	The sum of electronic and zero-point energies	TThe sum of electronic and thermal free energies	The sum of electronic and thermal enthalpies	The sum of electronic and thermal free energies
Energy/Hartrees	-234.469215	-234.461867	-234.460923	-234.500798

Optimization of the "Chair" and "Boat" Transition Structures

The transition states of cope-rearrangement of 1,5-hexadiene, chair conformation and the boat conformation shown in Figure X were optimized by using three methods. The structures of both transition states were shown in Figure X. Firstly the force constants were calculated under HF/3-21 G level.

Chair transition state optimization

Firstly an allyl fragment CH₂CHCH₂ was drawn and copied. Two fragments were combined together by choosing Append Molecule. The fragments were oriented and the distance between two terminal carbons of each fragments was set as 2.2 Å so that they were close enough for transition structure optimization.

Allyl Fragment
Structure	Energy	Point Group
		C2v

Two different methods were used to optimize the transition states. Both methods were carried out under HF/3-21 G level. The first method was the optimization by choosing Opt+Freq instead of optimization, and selecting optimization to a TS (Berny) with Opt=NoEigen as additional word. The second method was the frozen method involved the frozen of reaction coordinate and Opt=ModRedundant. The transition structures obtained from two methods were the same as shown in the table below. The transition structures optimized by using guess method and frozen method showed the presence of only one imaginary frequency at -817.94 cm^-1 and 817.89 cm^-1 respectively, confirmed that the transition structure meet the energy maximum as a transition state in the reaction pathway.

Chair transitions state
Structure	JSmol	Point group	Energy/Hartrees	Imaginary frequency/cm-1
		C2h	-231.619322	-817.94
		C2h	-231.619322	-817.89

Comparison of two methods

Boat transition state optimization

The optimization of boat transition state involved the use of QST2 method under HF/3-21 G level, the calculation via interpolation of structures of reactant and product. It is crucial to label the atoms of reactants and products in the same order. The optimized anti 2 conformers were copied as reactant and product, and numbered correctly followed by being oriented to adopt a pseudo boat structure. In both structures of reactant and product, the angles of C2-C3-C4 and C3-C4-C5 were set to 100^° and the dihedral angles of C2-C3-C4-C5 were set to 0^° and the modified structures were shown in the figure below. The left one is the reactant and the right one is the product. The structures were modified to adopt a half-boat conformation. The optimization was made by choosing QST2 under Opt+Freq option. A boat type of transition structure was worked out and there was only one imaginary frequency. It indicated that the transition structure meet the energy maxima at -840.23 cm^-1 as a transition state.

Structure	Energy/Hartrees	Results Summary	Imaginary Frequency/cm-1
	-231.602802		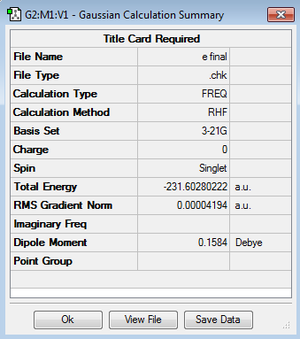-840.23

Intrinsic Reaction Coordinate (IRC)

The optimized chair transition structure was further studied by using IRC calculation under the HF/3-21 G energy level. As the reactant and product are the same, the reaction coordinate is symmetrical. Therefore the reaction coordinate can be computed in one direction only. The forward direction of IRC was chosen as the job type and calculation of force constants was set to be run for once. The number of points along the IRC was set to be 50 to observe the process of calculation. The progress was observed by allowing the presence of all of the geometries of intermediates when opening the chk file. The result of calculation is presented in the table below. The calculation converged at N=44 to give a gauche 2 conformation structure. The figure of RMS gradient norm along IRC showed that the gradient became approaching zero as the reaction coordinate increases. It correlated with the fact that the calculation converged at N=44. To confirm the success of analysis, the structure was re-optimized by setting the points to 65. The calculation converged at N=44 again.

Jmol	Energy/Hartrees	Calculation Summary	Structure at N=44
	-231.602802

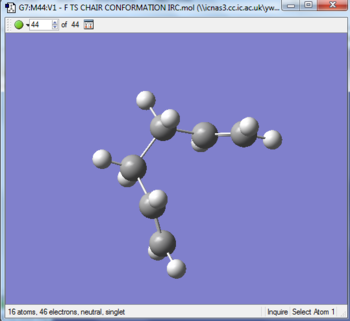
Structure
Total Energy along IRC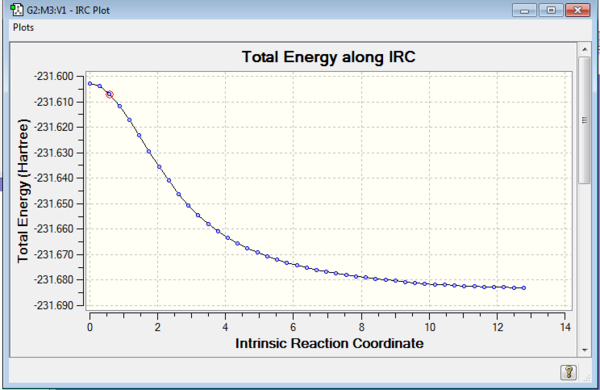
RMS Gradient Norm along I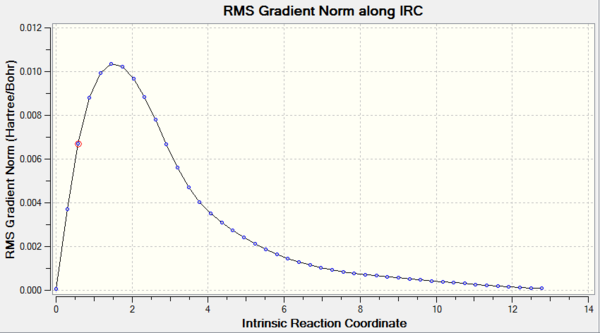

Energy comparison of chair and boat conformations

Both chair transition structure and boat transtition structure optimized from HF/3-21 G energy level were reoptimized by using DFT method with the level of B3LYP/6-31G*. The frequency calculation were also carried out. Both structures showed that there was only one imaginary frequency existing, confirming the adoption of of energy maximum.

Transition State	Calculation Summary	Imaginary Frequency
Chair
Boat

The table below showed the energy comparison of chair and boat conformations under different level of theory.

	HF/3-21 G	HF/3-21 G	HF/3-21 G	B3LYP/6-31 G*	B3LYP/6-31 G*	B3LYP/6-31 G*
Structure	Electronic Energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K	Electronic Energy	Sum of electronic and zero-point energies at 0K	Sum of electronic and thermal energies at 298.15 K
Chair TS	-231.619323	-231.466701	-231.461342	-234.556932	-234.414879	-234.408951
Boat TS	-231.602802	-231.450930	-231.445302	-234.543093	-234.402342	-234.396008
Anti 2	-231.692535	-231.539539	-23.532565	-233.611771	-234.469215	-234.461867

Activation Energy were calculated and presented in kcal/mol instead of Hartrees as shown in the table below. The experimental value of activation energy at 0 K for chair transition state is 33.5 ± 0.5 and 44.7 ± 2.0 respectively. As the it can be concluded that the optimization under B3LYP/6-31 G* theory level is more reliable and accurate compared to HF/3-21 G. The main reason is that the electron-electron interaction is ignored during the calculation under HF/3-21 G level, but is considered under B3LYP/6-31 G* level.

Transition state	HF/3-21 G at 0 K	HF/3-21 G at 298.15 K	B3LYP/6-31 G at 298.15 K	B3LYP/6-31 G* at 0 K
Chair TS	45.68	44.70	34.08	33.19
Boat TS	55.60	54.71	41.95	41.32

The Diels Alder Cycloaddition

The Diels Alder Cycloaddition reaction of ethylene and cis-butadiene

The Diels Alder reaction is a [4+2] concerted cycloaddition of a electron-rich diene with electrophilic dienophile, producing a cyclohexene system. It is a type of concerted pericyclic reaction as the simultaneous bond formation and breaking of 4π and 2π systems are suprafacial therefore the interaction is thermally allowed. The reactivity of reaction can be studied by applying frontier molecular orbitals theory. In a normal demand cycloaddition, the HOMO (highest occupied molecular orbital) is the Ψ2 orbital of diene and the LUMO (lowest unoccupied molecular orbital) is the π* orbital of dienophile. The interaction of HOMO and LUMO orbitals allows the reaction to occur. But the reverse demand cycloaddition can occur with respect to the change of substituents of diene and dienophile. The electron withdrawing group would lower the energy level of Ψ3 of diene, while the electron donating groups would increase the energy level of π of dienophile, resulted in a reversed HOMO-LUMO interaction.

(This MO notation should be defined somewhere Tam10 (talk) 11:55, 11 March 2016 (UTC))

The [4+2] concerted Diels Alder cycloaddition is stereospecific as the stereochemistry of the products are remained from reactants. The reaction occurs via a transition state instead of intermediate. There are two forms of transition states, endo and exo can be formed from the cycloadditon reaction of diene with dienophiles, resulting in endo product and exo product respectively. The stereoselectivity of reaction is predicted by endo rule which predicted that the kinetic endo product dominated over thermodynamic exo product. The endo product takes advantageous over exo product due to the secondary orbital stabilization of the π system of dienophile with diene.

Optimization of ethylene and cis-butadiene

The structures of ethylene and cis-butadiene were cleaned and optimized under Semi-Empirical (AM1) energy level to reach a minimum energy level. The structures, energy and point group are shown below.

Name	Structure	Point Group	Energy/Hartrees
Ethylene		D2h	0.026190
Cis-butadiene		C2v	0.048797

(This cis-butadiene is not a true minimum with a dihedral of 0º. Perform a frequency analysis to confirm that you have a minimum Tam10 (talk) 11:55, 11 March 2016 (UTC))

The HOMO and LUMO of both molecules are illustrated below. It is clearly shown that the HOMO of cis-butadiene is antisymmetric while the LUMO is symmetric around the carbon carbon single bond. In contrast, the HOMO of ethene is symmetric while the LUMO is antisymmetric around the carbon carbon double bond.

Orbital Type	cis-Butadiene	Ethene
HOMO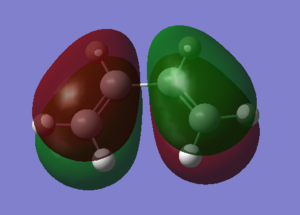
LUMO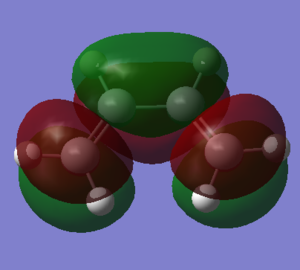

Optimization of transition state of reaction

Firstly, a guess transition structure was drawn by copying and orienting the optimized ethylene and cis-butadiene. An optimization of guess transition structure was carried out by choosing Opt+Freq with the option optimizing to Berny Algorithm using Empirical method under AM1 energy level. The results of optimization is illustrated in the table below. The presence of imaginary frequency at -956.18 cm^-1 confirmed that the transition structure reached the maximum energy and hence indicated the transition state was obtained by using this method. The animations of molecule at imaginary frequency and the lowest real frequency are also shown below. The animation of transition state at imaginary frequency showed that the formation of two sigma bonds are synchronous. And it reflected that the simultaneous bond broken and bond formation were suprafacially in both π₂ of ethylene and π₄ of cis-butadiene electronic systems. According to the Woodward-Hoffman rule, the reaction is thermally allowed as the value of (4m)_a+(4n+2)_s in this system is odd. In the animation of transition structure at lowest positive frequency, the ethylene component did not tend to approach the cis-butadiene component. It could be concluded that the bond formation did not occurr at this frequency and therefore the mode at lowest real frequency was not involved in the reaction pathway. The geometry of transition state was also investigated and studied by comparing with experimental data. The typical sp³ C-C single bond length is 1.54 Å and the bond length of sp² C-C double bond is typically 1.34 Å. The length of single C-C bond of cis-butadiene in transition structure is 1.39747 Å, much shorter than the normal C-C bond length from literature. From observation, the double bond of both cis-butadiene and ethylene in transition structure increased to 1.38184 Å and 1.38295 Å respectively. It could be explained by the the interaction of p orbitals during bond broken. The distances between the terminal carbon of cis-butadiene and ethylene were lengthened to the value of 2.11927 Å, which is smaller than twice of the van der Waals radii of carbon (van der Waals raddi of carbon is typically 1.70 Å from literature). This phenomenon is a result of formation of two new sigma bonds.

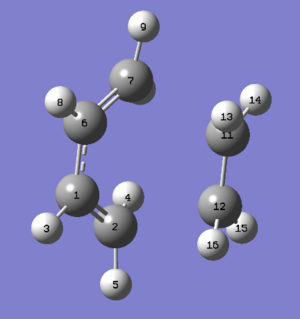
	C1-C6	C1-C2	C2-C12	C12-C11
Bond length/Å	1.39747	1.38184	2.11927	1.38295

Click here to the link of log output file of transition state calculation.

The HOMO and LUMO of transition states were shown in the table below. From the molecular orbitals shown in the table, it could be concluded that the HOMO of transition state is antisymmetric while the LUMO of transition state is symmetric with respect to the central of structure. The antisymmetric HOMO of transition state is resulted from the interaction of ethylene LUMO orbital with cis-butadiene HOMO orbital, which are both antisymmetric orbitals. And the symmetric LUMO of transition state is a combination of symmetric LUMO of cis-butadiene and symmetric HOMO of ethylene.

Structure	Energy/Hartrees	HOMO	LUMO
	0.111655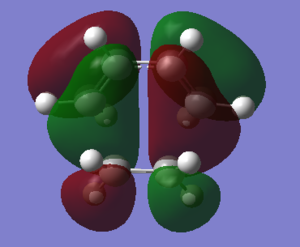

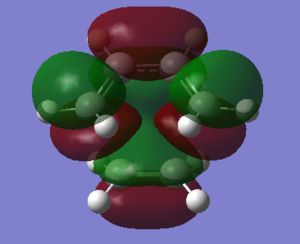
Frequency type	Frequency/cm-1	Animation
Imaginary Frequency	-956.18
Lowest Real Frequency	147.25

The Diels Alder Cycloaddition reaction of 1,3-Cyclohexadiene and Maleic Anhydride

The reaction of Diels Alder cycloaddition reaction of 1,3-cyclohexadiene and maleic anhydride is shown in the figure below. The maleic anhydride is a typical dienophile that favours the endo product according to Alder rule. The reaction scheme is shown below.

Optimization of 1,3-Cyclohexadiene and Maleic Anhydride

The optimization was carried out using the semi-empierical method under AM1 energy level. The structures of maleic anhydride and 1,3-cyclohexadiene were created and cleaned, followed by the minimization of energy achieved by optimization. The success of minimization of energy was confirmed by the lack of imaginary frequency. The results were shown in the table below. The HOMO orbitals of maleic anhydride and the LUMO of 1,3-cyclohexadiene are symmetric while the LUMO of maleic anhydride and the HOMO of 1,3-cyclohexadiene are antisymmetric.

Name	Structure	Point Group	Energy/Hartrees
Maleic Anhydride		C2	-0.121824
1,3-Cyclohexadiene		C2v	0.027711

Orbital Type	Maleic Anhydride	1,3-Cyclohexadiene
HOMO
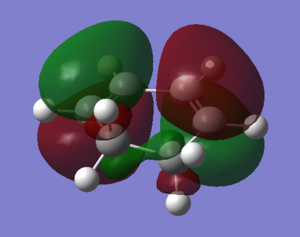
LUMO

Exo Transition State

In this section , two methods were used to obtain a transition state for the formation of Exo product. One was the optimization of guess transition state with the requirement of high similarity to real transition structure and the other was the QST2 method which required the reactant and product optimization and number labelling of each atom. Both methods were carried out under semi-empirical/AM1 energy level. The exo product was drawn, cleaned and optimized to minima energy level. After the guess product was optimized to adopt minimum energy with only positive frequency values, the terminal carbon atoms of two components were set to be 2.2 Å apart from each other. Then the modified structure was carried out by choosing the Job work type as Opt+Freq minimizing to TS (Berny) with calculating force constant once. Opt=NoEigen was typed into the additional word box to disrupt the calculation if more than negative frequency value was present. To carried out the second method, firstly the structures of product and reactant were drawn and optimized, followed by numbering them in order. And then the job work Opt+Freq was chosen and replaced the option TS (Berny) with QST2. The input structures of reactant and product were shown in the table below.

Reactant	Product

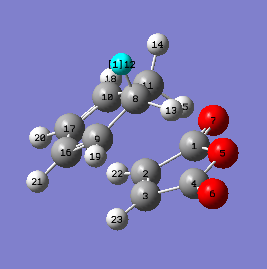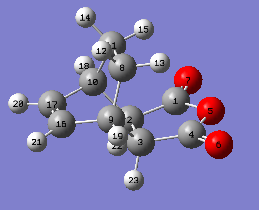
The optimization and frequency calculation via two varied methods were successfully carried out, and the results were shown in the table below. Both optimized transition states were confirmed as there was only one imaginary frequency present at around -812 cm^-1.

Method	Structure	Energy/Hartrees	Imaginary frequency/cm-1	Imaginary Frequency animation	Calculation Summary
QST2		-0.050419	-812.40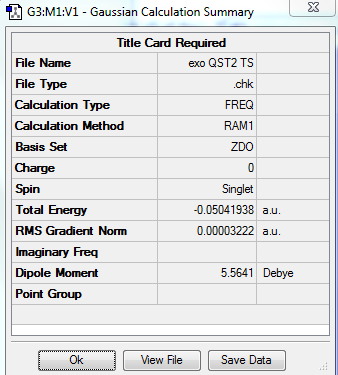
TS(Berny)		-0.050420	-812.23

The observation of MOs showed that both HOMO and LUMO of exo transition states are antisymmetric with respect to the carbon carbon double bond of alkene.

HOMO	LUMO

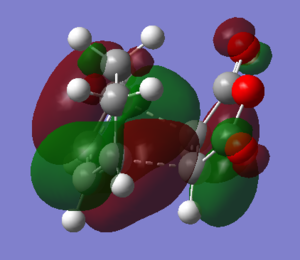Endo Transition State

The endo transition state was found by using the QST2 method by following the same procedures as described in the exo transition state session. The numbered structures of reation and product, the results of transition structures were illustrated below. A negative frequency value at 806.40 cm^-1 was present as the only existing imaginary frequency, indicating the successful optimization of endo transition state.

Reactant	Product

Transition Structure	Energy/Hartrees	Imaginary Frequency/cm-1	Imaginary Frequency Animation	Calculation Summary
	-0.051505	-806.40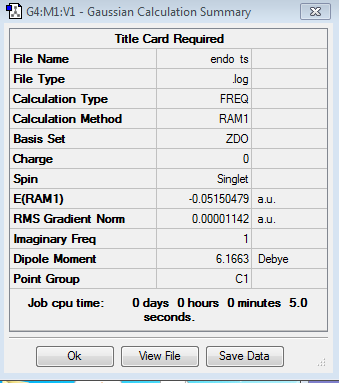

The LUMO and HOMO of exo transition state were observed as antisymmetric MOs.

HOMO	LUMO

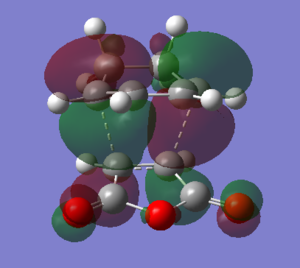Comparison of endo and exo transition state

The geometry of two transition states were compared. From literature, the sp³ C-C single bond length is 1.54 Å, while the sp² C=C double bond is 1.47 Å. The van der Waals radii of carbons are 1.7 Å. The distance between C₂ and C₁₀ in endo TS is is 2.16234 Å while the distance in exo TS is 2.17047 Å. Both distances are smaller than twice of van der Waals radii as a result of bond formation. However, the length of new sigma bond formed in endo TS is smaller than exo TS, due to the stronger orbital interaction of two components in endo TS.

The energies of reactants, exo transition state and endo transition state are shown in the table below. The activation energies were obtained from the electronic ernergy and thermal energy at 298.15 K. By comparision, the activation energy of endo TS is lower in energy than exo TS and therefore the endo product is formed faster than exo TS in irreversible reactions as a kinetic product. The maleic anhydride had C=O pi system, that could interact with the pi system of 1,3-cyclohexadiene, therefore the activation energy of endo TS is lower than exo TS due to the secondary orbital stabilization of endo TS according to the Alder rule.

(You should go further into discussing the differences in sterics between the side-groups of each TS, as well as secondary orbital contributions Tam10 (talk) 11:55, 11 March 2016 (UTC))

	Maleic Anhydride	1,3-Cyclohexadiene	Exo TS	Endo TS
Sum of Electronic energy and zero point energy at 0 K/ Hartrees	-0.063346	0.152502	0.134880	0.133494
Sum of Electronic energy and thermal energy at 298.15 K/Hartrees	-0.058192	0.157726	0.144881	0.143683

	Exo TS	Endo TS
Activation Energy at 0 K/kcal mol-1	28.70	27.83
Activation Energy at 298.15 K/kcal mol-1	28.47	27.71

Further discussion

The production bi-products are neglected in the calculations. In practical experiment, there are the potential issues such as difficulty of dissolution. The undissolved reactants have the potential to dimerize. The solvent effect is also not considered. However, solvents such as water have the potential to affect the reaction pathway.

Conclusion

In summary, both cope rearrangement and Diels Alder cycloaddition were studied by using Gauss View 5.0. The results of calculation of different transition states were compared and related to the mechanisms. The IRC was carried out to investigate whether the optimized transition structure is involved in the reaction pathway. Two varied methods for optimization of transition structures, Berny algorithm and QST2 were both carried out. The optimization of cycloadditions are expected to be carried out by using B3LYP/6-31 G* method at different temperatures for comparison of energies in future.