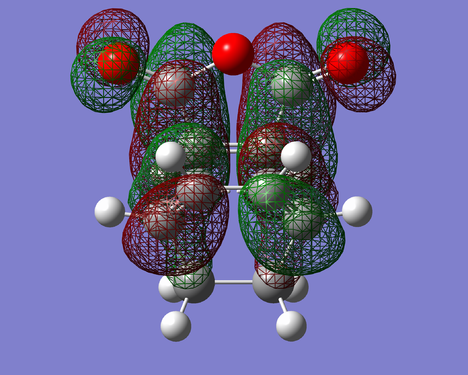
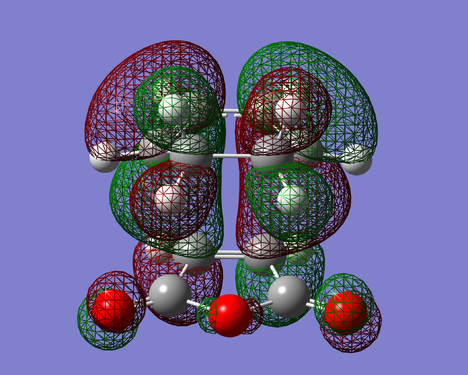
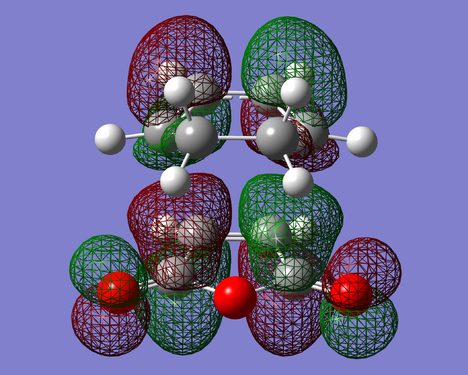
Rep:MOD:XW1995
Module 3 Introduction
In the computational excercise, the transitions structures of the Cope rearrangement of 1,5-hexadiene and other two Diels-Alder cycloaddition reactions were studied. By using the molecular orbital-based methods, the transition states could be located on the potential energy surface. The reaction paths and the barrier heights could also be calculated.
-
The Cope rearrangement of 1,5-hexadiene
-
The Chair and Boat TS in the Cope rearrangement
-
Diels-Alder reaction
(Please reference these images, or make your own versions Tam10 (talk) 12:10, 10 December 2015 (UTC))
The Cope rearrangement of the 1,5-hexadiene was a [3,3]-sigmatropic rearrangement which involved the formation and breaking of bonds in a conjugated π system while the Diels-Alder cycloaddition reaction between diene and dienophile involved the formation of two δ bonds. Both reactions had two transition structures, the optimisations and calculations of GaussView were used to investigate the structures of these TS, the energy barrier heights and the reaction paths.
Nf710 (talk) 10:27, 16 December 2015 (UTC) This is a pretty brief intro. You have understood the organic chemistry behind the processes however you havent shown any understanding of the computational methods used here.
GaussView and Gaussian were used.
The Cope Rearrangement
Optimising the Reactants and Products
Three conformers of 1,5-hexadiene were obtained in this section and the energy values of each conformer in the summary was used to determine the corresponding structure type by comparing with the data in Appendix 1 of the script.
| Conformer | Structure | Point Group | Energy /Hartree | Log File |
|---|---|---|---|---|
| Anti 1 |  |
C2 | -231.69260235 | File:XW-ANTI-1.LOG |
| Anti 2 | 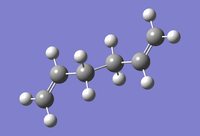 |
Ci | -231.69253528 | File:XW-ANTI-2.LOG |
| Gauche 3 | 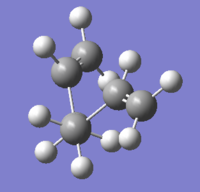 |
C1 | -231.69266120 | File:XW-GAUCHE-3.LOG |
The two anti-conformers were obtained by the optimisation of the strating molecule with the anti-linkage of the four central carbon atoms, while the gauche-conformer was from the starting molecule with the gauche-linkage.
The lowest energy conformer was the Gauche 3 confromer of 1,5-hexadiene as both Table 1 above and Appendix 1 shown.
By considering the sterics and symmertry, different dihedral angles of the four central carbon atoms could lead to different sterics. The conformation of Gauche 3 could have the smallest overall steric repulsions/hindrance between atoms, and therefore was the most relaxed conformation as its symmertry was C1 which was relatively lower than other conformers as well.
Nf710 (talk) 10:29, 16 December 2015 (UTC) Gauche 3 is the lowest due to the secondary orbital overlap which you can show in the .chk file.
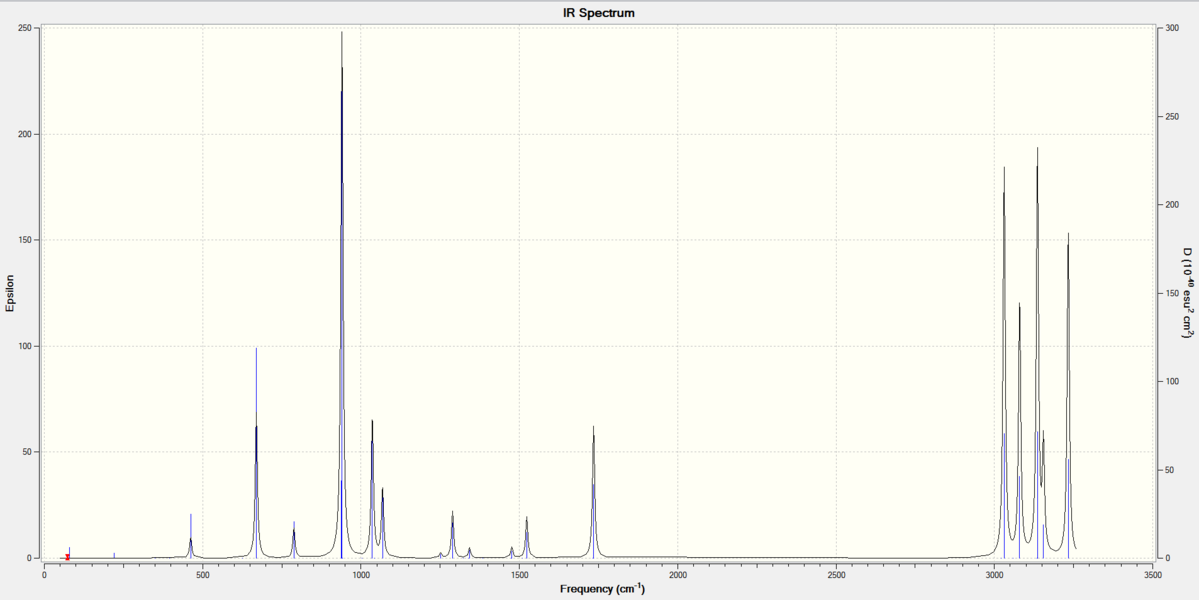
The Anti 2 was then re-optimised at B3LYP/6-31G* level, this re-optimisation was to lower the energy of the conformer as the values in the Table 2 shown, and then the frequency calculation was applied. The results then showed no imaginary frequencies (negative frequency) in the spectrum as Figure 1 shown below, which indicated it was the minimum at this stage.
-
Figure 1. IR spectrum of the re-optimised Anti 2 conformer at B3LYP/6-31G* level
Table 2. Summary of energies of Anti 2 (in Hartree)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energy | Sum of electronic and thermal energy | Electronic energy | Sum of electronic and zero-point energy | Sum of electronic and thermal energy | |
| Anti 2 conformer | -231.69253528 | -231.527833 | -231.520862 | -234.61171100 | -234.469222 | -234.461871 |
Although the re-optimisation of Anti 2 conformer did not change the dihedral angle of the four central carbon atoms, the bond lengths and the other bond angles were changed.
In HF/3-21G level optimisation, the C=C-C angle was 124.8 degrees and the C-C-C angle was 125.3 degrees, the C=C bond was 1.316 Å, the single C-C bond in C=C-C was 1.509 Å and the central C-C bond of C-C-C-C was 1.553 Å.
In B3LYP/6-31G* level re-optimisation, the C=C-C was decreased to 111.3 degrees and the C-C-C angle was decreased to 112.66571 degrees, the C=C bond was 1.333 Å, the single C-C bond in C=C-C was 1.504 Å and the central C-C bond of C-C-C-C was 1.548 Å.
All data values above showed that there was a decrease in the bond angles and bond lengths after the B3LYP/6-31G* level re-optimisation.
LOG File:
Nf710 (talk) 10:32, 16 December 2015 (UTC) Your energies here are correct however you haven't included the thermochemistry data. good geom comparison.
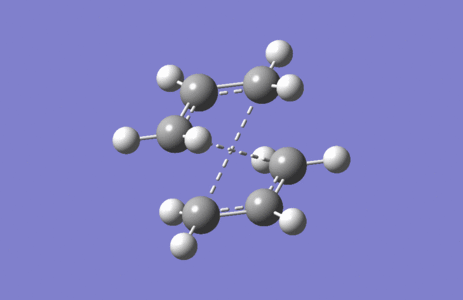
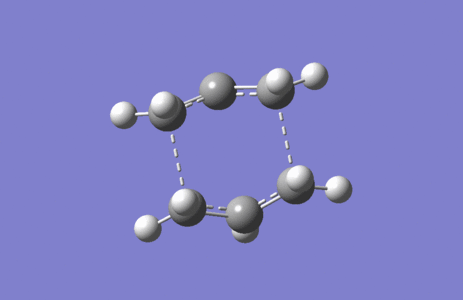
Optimising the "Chair" and "Boat" Transition Structures
Optimisation of Chair and Boat TS
The Freeze Coordinate and Derivative methods were used in this part. The optimisation was to use the TS Berny for the guess structure first and then the optimisation using the QST2 method was applied to find the transition states.
The point group of the Chair TS was found to be C2h and the point group of the Boat was C2v.
-
Figure 2. Reactant and Product for Chair TS
-
Figure 3. Reactant and Product for Boat TS
-
Figure 4. Imaginary vibration of Chair TS
-
Figure 5. Imaginary vibration of Boat TS
Note: The vibration animations could be watched from the original gif files.
Optimised at HF/3-21G level, both transition states only had one imaginary frequency where the Chair transition state was at -818.15 cm-1 while the Boat transition state was at -839.65 cm-1.
The frequency was related to the second derivatives of the energy reaction path of a reaction. The transition state was a well-defined saddle point in the energy-path diagram, the negative frequency indicated there was a stationary point which was a energy maxima. Therefore, the only one imaginary frequency could confirmed the transition states.
The bond lengths between the two terminal carbons of each terminal carbon pair which was to form new bond of the Chair TS using this method were determined to be 1.96628 Å and 1.96628 Å.
The bond lengths between the two terminal carbons of each terminal carbon pair which was to form new bond of Boat TS were found to be 2.20626 Å and 2.20642 Å which were longer than in Chair TS.
Nf710 (talk) 10:35, 16 December 2015 (UTC) Correct frequencies but poorly formatted and discussed. No understanding of how the frequency analysis works
IRC Calculations
The forward direction, force constant calculated once and No. of points = 50 were used.
-
Figure 6. Chair TS IRC path
-
Figure 7. Boat TS IRC path
Note: The vibration animations could be watched from the original gif files.
-
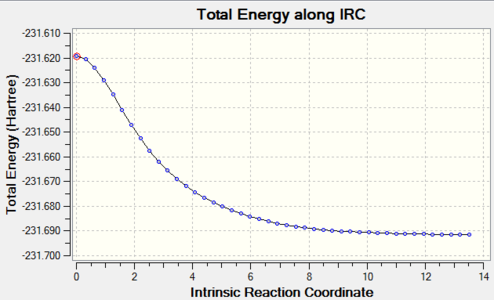
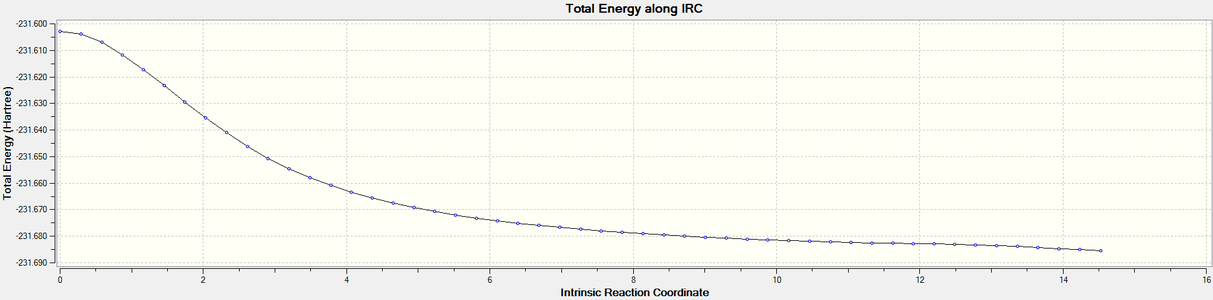
Figure 8. Chair TS IRC result_Total energy along the IRC
-
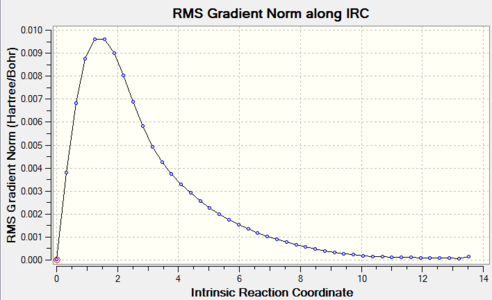
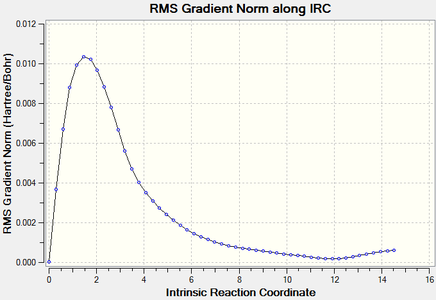
Figure 9. Chair TS IRC result_RMS Gradient Norm
-
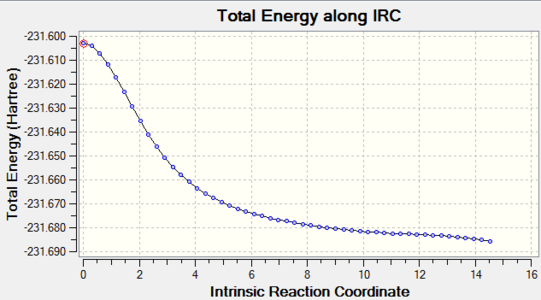
Figure 10. Boat TS IRC result_Total energy along the IRC
-
Figure 11. Boat TS IRC result_RMS Gradient Norm
The peaks in the RMS Gradient Norm graphs confirmed the transition states.
However the energies shown in the graphs still had not reached the minimum as the RMS gradient was still not zero, to be closer to minimum, IRC calculations at the same level were applied again to both transition structures and the data were obtained below.
-
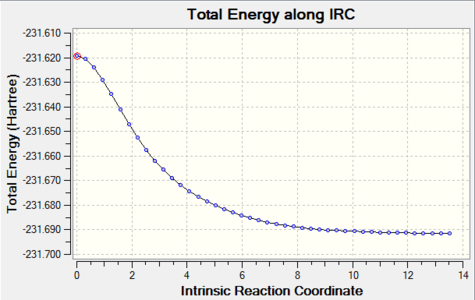
Figure 12. Chair TS re-IRC result_Total energy along the IRC
-
Figure 13. Chair TS re-IRC result_RMS Gradient Norm
-
Figure 14. Boat TS re-IRC result_Total energy along the IRC
-
Figure 15. Boat TS re-IRC result_RMS Gradient Norm
The graphs above showed the minimum still had not to be reachedas RMS gradient was still not zero, so more IRC calculations should be tried.
Nf710 (talk) 10:37, 16 December 2015 (UTC) Well done lots of IRCs here. You have at least one which is good.
Activation Energies Determination
Table 3. Summary of energies (in hartree)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| Chair TS | -231.61932234 | -231.466704 | -231.461344 | -234.55692629 | -234.414920 | -234.408989 |
| Boat TS | -231.60280222 | -231.450928 | -231.445299 | -234.54307872 | -234.402355 | -234.396010 |
| Reactant (Anti 2) | -231.69253528 | -231.527833 | -231.520862 | -234.61171100 | -234.469222 | -234.461871 |
Table 4. Calculated Activation Energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |
| ΔE (Chair TS) | 38.36 | 37.35 | 34.07 | 33.18 |
| ΔE (Boat TS) | 48.26 | 47.42 | 41.96 | 41.33 |
The activation energies obtained in Table 4 were calculated directly from the data in the Table 3 and 1 hartree = 627.509 kcal/mol[1] was used.
The experimental activation energies are 33.5 ± 0.5 kcal/mol[1] for the Chair transition structure and 44.7 ± 2.0 kcal/mol[1] for the Boat transition structure at 0 K.
As shown in the Table 4, the calculated activation energies at 0K showed that the re-optimisation at B3LYP/6-31G* level gave the values which were closer to the experimental values.
Therefore, the calculation method of B3LYP/6-31G* could lead to structures which were more accurate and a better model of the real structure.
Nf710 (talk) 10:42, 16 December 2015 (UTC) your energies are correct. however you havent compared the geoms between the the re optimised TS or checked imaginary frequencies. This is a fairly good report and you have done most of the things that were asked of you however you have shown minimal understanding of the methods used.
LOG Files:
Diels-Alder Cycloaddition Reaction
In this section, the basic method to obtain the transition structure was using the optimised reactants as the fragments and then justify the bond distances close to the known ones of transition structures and then the TS calculations was applied.
Cis Butadiene with Ethylene
Reactants optimisation
Both reactant molecules were optimised using AM1 semi-empirical method an then re-optimised at B3LYP/6-31G* level.
-
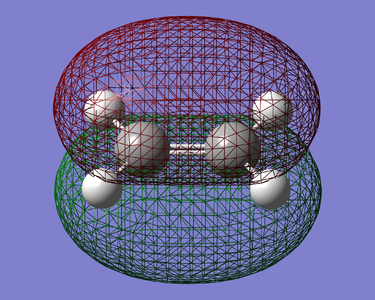
Figure 16. HOMO of Butadiene(Anti Symmetric)
-
Figure 17. LUMO of Butadiene(Symmetric)
-
Figure 18. HOMO of Ethylene(Symmetric)
-
Figure 19. LUMO of Ethylene(Anti Symmetric)
LOG Files:
Transition Structure
To obtain the TS, the guessed TS was drawn as the script sugussted, the bond distances between the two carbon atoms of each terminal carbon pair of the reactants were set to be 2.2 Å which was the same as the values used in the Cope rearrangement tutorial.
And then the structure was optimised using the TS Berny with Opt=NoEigen and Force Constant Calculated Once at AM1 semi-empirical level.
After that, the TS obtained ws appied to IRC calculation to confirm the structure and the IRC path was shown in Figure 20 below.
Only one imaginary frequency was observed in the IR spectrum and the vibration was shown in Figure 21 below.
And this imaginary vibration was symmetric to the nodal plane which indicated the the system of the TS was synchronous/concerted.
The IRC calculation of the transition structure was carried out in both directions and the Figure 20 shown below, the peak appeared at 0 confirmed the structure obtained was indeed the transition state which was a energy maxima.
-
Figure 20. IRC results of transition state_Total energy along IRC
-
Figure 21. Imaginary vibration of TS
Note: The vibration animations could be watched from the original gif files.
-
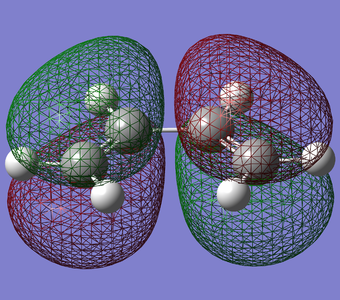
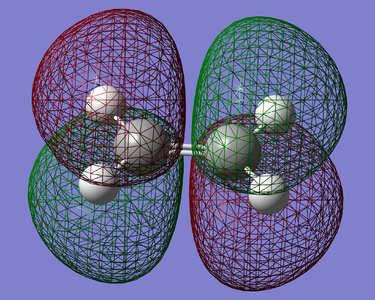
Figure 22. HOMO of TS (Anti Symmetric)
-
Figure 23. LUMO of TS (Symmetric)
(This is a pretty strange MO. It's definitely not antisymmetric here though. It looks like these are the HF MOs, not the AM1 MOs Tam10 (talk) 12:34, 10 December 2015 (UTC))
As shown above, the HOMO of TS obtained was anti symmetric. Therefore, the HOMO of transition state was formed by the anti symmetric HOMO of cis-butadiene and the anti symmetric LUMO of ethylene.
In the Pericyclic course, the Woodward-Hoffman Rules which stated that the reaction was thermally allowed when the sum of (4q +2)s + (4r)a is odd, where the q and r were the corresponding number of s (suprafacial) and a (antarafacial) components that were related to the π electrons in each π system of the reactant molecule was used as the basic principle.
By considering and counting the orbitals and number of electrons involved, the sum of the (4q +2)s + (4r)a was odd for this reaction. Therefore, the reaction was thermally allowed and the formation of the HOMO of TS was s (suprafacially), and it was symmetry allowed and the formation was synchronous which meant concerted as the imaginary vibration in Figure 21 indicated.
| Bond | 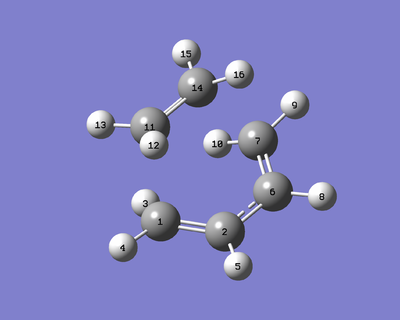
|
| C1-C11 | 2.11895 |
| C7-C14 | 2.11979 |
| C2-C6 | 1.39764 |
| C4-C11 | 1.38314 |
| C7-C6 | 1.38196 |
| C1-C2 | 1.38173 |
As shown in Table 5, the distances between the terminal carbon atoms where the new two σ bonds to be formed were longer than 1.54 Å [2] which was the sp3 C-C bond length, but it was shorter than 3.4 Å which was calculated result as the sum of two carbon atoms's VDW (Van Der Waals) radius, which indicated the interactions between these carbons did exist in TS but were weaker than C-C single bond in an alkane.
The typical sp2 C-C bond length was 1.47 Å [2] but the bond length in alkene was 1.34 Å [2]. The other four bonds lengths in TS were greater than 1.34 Å but smaller than 1.54 Å, so their characters were between C=C in alkene and C-C in alkane, which confirmed the transition state.
LOG File:
Maleic Anhydride with Cyclohexa-1,3-diene
In this part, the two reactant molecules were optimised first, and then the guessed ENDO and EXO transition structures were both drawn as the script suggusted. The bond distances between the two carbon atoms of each terminal carbon pair of the reactants were set to be 2.2 Å which was the same as the values used before.
These two guessed TS structures were then optimised using the TS Berny and with Opt=NoEigen and Force Constant Calculated Once at AM1 Semi-empirical level.
However, the re-optimisation method used for the two TS was HF/3-21G level, because the B3LYP/6-31G* calculation always failed with damaged output files when trying to obtaining the re-optimised transition stuctures.
Both transition states showed that only one imaginary frequency appeared in the IR spectrum and the vibrations were shown below.
-
Figure 24. Imaginary vibration of ENDO-TS
-
FIgure 25. Imaginary vibration of EXO-TS
Note: The vibration animations could be watched from the original gif files.
-
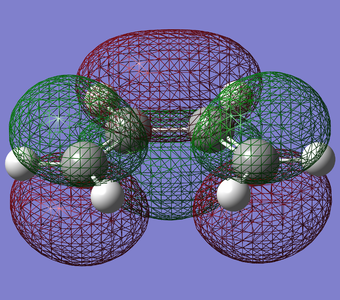
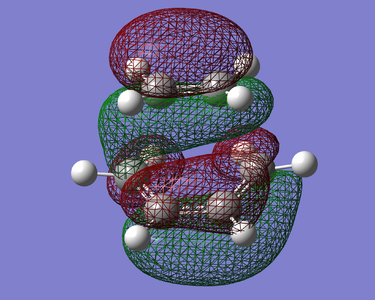
Figure 26. HOMO of ENDO-TS(Anti Symmetric)
-
Figure 27. LUMO of ENDO-TS(Anti Symmetric)
-
Figure 28. HOMO of EXO-TS(Anti Symmetric)
-
Figure 29. LUMO of EXO-TS(Anti Symmetric)
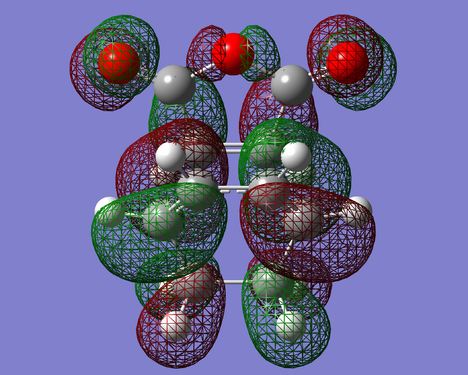
As the HOMO and LUMO of each TS shown in Figure 26, Figure 27, Figure 28 and Figure 29 above, all four molecular orbital overlaps did not involve the lone pair in the p-orbital from the oxygen atoms of -(C=O)-O-(C=O)- of maleic anhydride as they were directly shown above.
Secondary orbital overlap was defined as the positive overlap of a non-active frame in the frontier molecular orbitals of a pericyclic reaction.[3]
This secondary orbital overlap could only be found in ENDO TS.
In the HOMO of ENDO TS, the overlap/interaction between the orbitals of carbon atoms of -(C=O)-O-(C=O)- in maleic anhydride with the oribitals of the central two carobon atoms of -C=C-C=C- in cyclohexadiene was observed as the arrangement of the two reactants allowed the interaction/overlap to occur. And this overlap/interaction was absent in the HOMO and LUMO of EXO TS.
This secondary overlap wsa a positive overlap which was favoured as it could lead to the stabilisation of the TS.
Table 6. Bond lengths/distances of Exo-TS and Endo-TS (in Å)
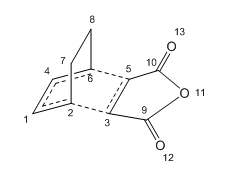
| ||
|---|---|---|
| Bond | ENDO-TS | EXO-TS |
| C5-C6 | 2.26115 | 2.23103 |
| C2-C3 | 2.26045 | 2.23096 |
| C1-C4 | 1.39744 | 1.39620 |
| C3-C5 | 1.37318 | 1.37015 |
| C1-C2 | 1.37016 | 1.37075 |
| C4-C6 | 1.37009 | 1.37075 |
As Table 6 showed, the distances between the terminal carbon atoms where the new two σ bonds to be formed were longer than 1.54 Å and shorter than 3.4 Å, which indicated the interactions between these carbons did exist in both TS but were weaker than C-C single bond in an alkane.
The other four bonds lengths in TS were greater than 1.34 Å which was the alkene C-C bond length but smaller than 1.54 Å, so their characters were between C=C in alkene and C-C in alkane, which confirmed the existance of both transition states. This was the same as the case of cis-butadiene with ethylene.
However, the bond length of EXO-TS of the bonds involved in the formation of the production was slightly smaller than the same bond of the ENDO-TS, which might be due to the greater electronic interactions of EXO-TS. So the EXO transition state might be slightly more strained.
Table 7. Summary of energies of the reactants and TS obtained
| Structure | Electronic Energy/Hatree |
| ENDO-TS | -605.61036831 |
| EXO-TS | -605.60359121 |
| Maleic Anhydride | -375.10351350 |
| Cyclohexa-1,3-diene | -230.53967069 |
(It looks like you haven't got a fully minimised CHD. Running a frequency job on your log file (thanks for uploading) shows that there's a negative frequency that attempts to break symmetry. If you distort the CHD with that imaginary frequency (results>vibrations>manual displacement) then rerun, you'll get the optimised CHD Tam10 (talk) 12:34, 10 December 2015 (UTC))
Table 8. Summary of Activation energies of Transition states
| Structure | Activation Energy (in Hatree) | Activation Energy (in kcal/mol) |
| ENDO-TS | 0.03282 | 20.59 |
| EXO-TS | 0.03959 | 24.85 |
In Table 8, the calculated activation energy of EXO-TS was greater than ENDO-TS as the electronic energy of EXO-TS was greater than ENDO-TS as shown in Table 7, which proved the ENDO transition state was kinetically favored TS. This was due to the less unfavorable steric repulsions and favourable secondary orbital overlap in ENDO-TS.
In this part, the symmetric cyclohexa-1,3-diene used as a reactant did lead to the similar basic shapes of the two TS. For ENDO structure, the -(C=O)-O-(C=O)- of maleic anhydride faced the -C=C-C=C- of cyclohexadiene. For EXO structure, the -(C=O)-O-(C=O)- of maleic anhydride faced the -C-C-C-C- of cyclohexadiene. Therefore the overall steric repulsion existed in each TS might just have small differences.
(Make some measurements to convince the reader of the effects of sterics Tam10 (talk) 12:34, 10 December 2015 (UTC))
But the ENDO TS had the secondary orbital overlap which was spatial positive interaction while EXO TS did not. This stabilisation allowed the ENDO TS to have lower free energy than EXO TS.
(Again, use a diagram to show this secondary orbital overlap Tam10 (talk) 12:34, 10 December 2015 (UTC))
LOG Files:
File:MALEIC ANHYDRIDE 3-21G.LOG
Further Discussion
Although the calculations and optimisations using Gaussian were to set models and structures, the basics of it was to use quantum mechanics.
The Born-Oppenheimer Approximation which assumed the nuclei fixed onle allowed to investigate electron distribution, the Gaussian used was to use the single electron Schrodinger equation. However, to use the single electron Schrodinger equation, the electrons were assumed to be independengt which meant did not interact with each other. This assumption could sometimes lead the Gaussian results to be quite different from the experimental results.
The AM1 semi-empirical method used was to assume the differential diatomic overlap and the two-electron Hamiltonian component were negligible in the calculations.
The higher level B3LYP/6-31G* was to use DFT which indeed gave a better calculation result of energies than HF/3-21G, it was more accurate but errors could sometimes occur during the calculations which lead to damaged outputs.
References
- ↑ 1.0 1.1 1.2 ChemWiki, Mod:phys3, Available from: https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3 Cite error: Invalid
<ref>tag; name "wiki" defined multiple times with different content - ↑ 2.0 2.1 2.2 WIKIPEDIA, Bond Length, Available from: https://en.wikipedia.org/wiki/Bond_length [Accessed: 3rd December 2015]
- ↑ M. A. Fox , R. Cardona , N. J Kieiwet, Steric Effects vs. Secondary Orbital Overlap in Diels-Alder Reactions. MNDO and AM1 Studies, J. Org. Chem., 1987, 52(8), pp 1469-1474.