Introduction

The potential energy surface (PES) is the mathematical relationship between the energy of a molcule and its geometry. ^[1] By taking advantage of the Born-Oppenheimer approximation, the PES represents the electronic energy of the molecule at all possible arrangements of the atoms. Vibrational zero-point energy is sometimes added to the PES for increased accuracy.

For a molecule with N atoms, this represents a surface with 3N-6 dimensions (degrees of freedom for a non-linear molecule). Naïvely, this could be found by evaluating the energy of the molecule over all points in space using specific methods suitable for the molecule at hand. However, the effectively infinite number of possible configurations renders this approach computationally impossible. Luckily, during a reaction, only a limited "patch" of the PES is explored by the molecule, and any analysis of a reaction can be reasonably limited to studies of the reactants, products, and any surface that they traversed from the reactants to products (the reaction profile).

The reactants and products are (relatively) stable chemical species. Intuitively, they reside in minima on the PES - as stable chemical species, they tend to return to their configuration from slight perturbations. On the other hand, a reaction path is physical, and must necessarily be continuous and differentiable (where the PES itself might not be). In this case, a reaction profile joining two minima (i.e. reactants and products) will pass through one (or more) maxima along the reaction coordinate. These properties can be used to deduce structures from the PES.

Critical points on the PES

Both minima and maxima are stationary points on the PES. For a stationary point at $\vec{q}$ , the following relationship must hold:

$\nabla U (\vec{q}) = 0$ ,

where $\nabla$ is the gradient function, $\vec{q}$ is any geometric parameter (e.g. mass-weighted coordinates), and $U (\vec{q})$ is the potential energy surface. In order to determine if it is a local maximum or minimum, the second derivative test must be conducted. First, a square $n \times n$ matrix, where $n$ is the number of geometric parameters, can be defined:

$H_{i, j} = \frac{\partial^{2} U}{\partial \vec{q_{i}} \partial \vec{q_{j}}}$

where $H_{i, j}$ is the i-th and j-th term of the Hessian matrix, $H$ . The second partial derivative test is conducted by looking at the eigenvalue of the Hessian matrix at the stationary points $\vec{q}$ , assuming that $H$ is invertible: - If all eigenvalues are positive, $\vec{q}$ is at a local maximum. - If all eigenvalues are negative, $\vec{q}$ is at a local minimum. - If there is a mix of positive and negative eigenvalues, $\vec{q}$ is at a saddle point. - And inconclusive otherwise.

In essence, the second partial derivative test is looking at direction of the local curvature at the station points.

Nf710 (talk) 18:52, 28 March 2018 (BST) You have spoke about the eigenvalues upon diagonalisation of the Hessian Matrix, but the the eigenvectors. These are the nrmal modes they are linear combinations of the degrees of freedom and when you move back and forth along this vector this is the vibration that you see. I see you have put this in your next section.

Harmonic Approximation and the Transition State

When deviation from equilibrium stationary points are small, the harmonic approximation can be used. The general expression of the harmonic approximation is as follows:

$U \approx \frac{1}{2} \sum_{i, j = 1} \frac{\partial^{2} U}{\partial \vec{q_{i}} \partial \vec{q_{j}}} q_{i} q_{j}$

As the force is related to energy as well as position,

$\begin{aligned} \vec{F} & = - \nabla U \\ = - k \vec{X} \end{aligned}$

where $\vec{F}$ is the column vector of the forces $[\vec{F_{1}}, \vec{F_{2}}, . . .]^{T}$ , $X$ is the column displacement vector of the coordinates $[\vec{q_{1}}, \vec{q_{2}}, . . .]^{T}$ , and $k$ is the force tensor connecting the force to the displacement of the atoms from their equilibrium positions. The differential equation admits a solution of the form:

$\vec{F} = - ω^{2} \vec{X}$

where $ω$ is the frequency of vibration of the harmonic oscillator. It is obvious that it is an eigenvalue problem to obtain values of $ω$ , with the associated eigenvectors being the normal modes of vibrations. In practice, this is often referred to diagonalising the Hessian matrix, as the elements of the diagonalised matrix are the eigenvalues of the matrix. If we compare the form of the harmonic approximation with the second partial derivative test, it could be immediately seen that:

Nf710 (talk) 18:58, 28 March 2018 (BST) These equations are saying that omega squared and k are equivalent. There is a mass constant int here somewhere that you have forgotten.

$k_{i, j} = H_{i, j} = \frac{\partial^{2} U}{\partial \vec{q_{i}} \partial \vec{q_{j}}}$

We could then restate the relationship between curvature and vibration as follows:

The frequency of vibration is proportional to the square root of the local curvature at the point.
A local minimum along coordinate $q_{i}$ will have a positive frequency of vibration along coordinate $q_{i}$ ; and
A local maximum along coordinate $q_{i}$ will have an imaginary frequency of vibration ( $\sqrt{- x} = i \sqrt{x}$ ); and
A saddle point will have a mixture of positive and imaginary vibrational frequencies.

A transition state is defined to be a point on the PES that lies at the minimum along all coordinates, except for the reaction coordinate along which it lies at the maximum. ^[2] In this case, a transition state will have one and only one imaginary vibrational frequency in its structure.

From the transition state, optimization of the structure along the coordinate following the steepest descent (as informed by the imaginary vibration frequency or negative force constant) allows one to reach the reactant and product state. The path traced out by such a procedure is called the Intrinsic Reaction Coordinate (IRC), and may or may not represent an actual physical reactive path due to other energy contributions (e.g. vibrational, kinetic, etc.). In either case, the IRC allows us to understand the changes in the molecular geometry, along with its electronic properties and molecule wavefunction, through the course of an reaction.

Nf710 (talk) 19:01, 28 March 2018 (BST) This is a very god section you have clearly read beyond the script here. It would have been good to have a few for references so that i could check your facts properly. But this looks more or less correct.

Computational Approaches

In quantum mechanics, all information about a quantum system is encoded In its wavefunction, $Ψ$ . The wavefunction obeys the Schrödinger equation, generally stated (in its time-independent form) ss below:

$\hat{H} Ψ = E Ψ$

where $\hat{H}$ is the Hamiltonian operator and $E$ is the energy of the system. The Schrödinger equation is not analytically solvable in general, and many techniques have been developed since to find an approximate solution to the Schrödinger equation. One of the earliest approaches was the Hartree–Fock method. It was an ab initio computational method to directly compute the molecule wavefunction. Along with post-Hartree–Fock methods and alternatives approaches such as the Density Functional Theory (DFT). The different approaches share broadly similar features.

One of the most useful computational methods for finding the ground state solution is the variational method, based on the variational principle. It requires the use of trial solutions (ansatz), often a basis set of orbitals, to evaluate the energy eigenvalue. As the variational principle states that the true ground state has the lowest energy, the wavefunction (or rather coefficients to the basis set) can be found by locating the global minimum of the ansatz. Often, the basis set of orbitals are orthogonal to each other and uses either Slater Type Orbitals (STOs) or Gaussian Type Orbitals (GTOs) to save computation time.

Nf710 (talk) 19:07, 28 March 2018 (BST) This is excellent you could have put some equations into the the explamations, for something such as the basis set STO-3G

Different methods employ different formalism and assumptions to simplify calculations. For example, Hartree–Fock implies the mean-field assumption and ignores electron correlation. The ansatz for the variational method is the Slater determinant of the basis sets and solves for the molecular wavefunction directly. DFT works by recognising the equivalence of finding the electron density of the molecule with its ground state wavefunction, allowing the optimizing of a single electron Schrödinger equation, shortening computation time. Modern methods with hybrid functionals (e.g. B3LYP) may use features from both to obtain more accurate results.

Nf710 (talk) 19:07, 28 March 2018 (BST) HF does not ignore correlation. it it obtains the static correlation, just not the dynamic. This is why it is used in the XC functional of B3LYP.

Unlike the ab initio methods above, semi-empirical methods drastically shorten computation time by making assumptions and correcting for them using parameters. These can include the zero differential overlap assumption, reducing the computational complexity scaling from $N^{4}$ to $N^{2}$ , where $N$ is the number of electrons. One common semi-empirical method is the Huckle method for π-electrons. However, the parametrization requirement means that different parameters or assumptions must be used for different systems (valence electron vs п-electrons, transition metals, small vs heavy elements, etc.). When properly parameterized, semi-empirical methods can produce results more accurately than ab initio methods with much greater computation efficiency. Even if general purpose semi-empiricle methods (e.g. PM6) are less accurate than ab initio methods, its computational efficiency means that it is often used as an initial step in an optimization.

Nf710 (talk) 19:07, 28 March 2018 (BST) Good paragraph, I wouldn't say semi empirical are more accurate than some of the more advanced coupled cluster or post HF methods.

Experimental Methods

In this experiment, the Diels-Alder reaction was investigated in 3 different systems: reaction of butadiene with ethylene, reaction of cyclohexadiene with 1,3-dioxole, and reaction between o-xylylene and sulphur dioxide. The calculations are carried out with Gaussian 09 on Windows 7. Unless otherwise specified, initial geometry optimizations and IRC calculations were carried out in PM6 at default settings, with IRC calculations allowed to carry out to PES minima. Reactant, product and transition state molecular orbital calculations were carried out with B3LYP/6-31G(d) unless otherwise specified.

Results were extracted and analysed with GuassView (v5.0.9), as well as with cclib (v1.5) on Jupyter Notebook using Python (v3.6.4). Python analysis script is available on request. Surfaces were visualized via generation of Cube files from Gaussian, then converted to .jvxl files for faster loading and subsequently visualized on JSmol.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Unfortunately this section is very confused. The MO diagram is incorrect, and even though you have correctly stated the symmetry requirements for the combination of reactant fragment orbitals you did not apply that to your computed orbitals. Additionally you didn't include jmols or log files so it is impossible to know if you have uploaded the wrong pictures or ran the wrong calculation.)

The reaction between buta-1,3-diene with ethene is the simplest example of a Diels-Alder reaction. The Diels-Alder reaction is a concerted pericyclic reaction between a diene (i.e. buta-1,3-diene) and a dieneophile (i.e. ethene). It in general proceeds via a single transition state with no intermediates, and is thus classified as a [4π_S+2π_S], and is thermally allowed under the Woodward-Hoffmann rules.

Using the Hückel method, we could restrict our analysis to only π-electrons. An illustration of the molecular orbitals is found in Figure 2. It is important to note that there are additional interactions betwene the sigma and pi frameworks of the molecules. From the MO diagram, it could be seen that there are significant interactions throughout the pi system. For example, the TS orbital π_3s is due to the net interaction of 3 orbitals: butadiene π_1s and π_3s, and ethene π_1s. Using frontier orbital molecular theory, we could further simplify analysis by, looking at only the HOMO/LUMO of the reactants and their interactions.

	Buta-1,3-diene	Transition State		Ethene
LUMOs	Figure 3a: Molecular orbital of the LUMO of buta-1,3-diene (MO 12, energy = +0.01104 a.u.). Corresponds to π_3s from Fig 2.	Figure 5a: Molecular orbital of the LUMO of the TS (MO 16, energy = -0.32755 a.u.). Corresponds to π_5a from Fig 2.	Figure 5b: Molecular orbital of the LUMO+1 of the TS (MO 17, energy = -0.32533 a.u.). Corresponds to π_3s from Fig 2.	Figure 4a: Molecular orbital of the LUMO of ethene (MO 7, energy = +0.04256 a.u.). Corresponds to π_4s from Fig 2.
HOMOs	Figure 3b: Molecular orbital of the HOMO of buta-1,3-diene(MO 11, energy = -0.35169 a.u.). Corresponds to π_2a from Fig 2.	Figure 5c: Molecular orbital of the HOMO-1 of the TS MO 18, energy = +0.01732 a.u.). Corresponds to π_3s from Fig 2.	Figure 5d: Molecular orbital of the HOMO of the TS (MO 19, energy = +0.03067 a.u.). Corresponds to π_2a from Fig 2.	Figure 4b: Molecular orbital of the HOMO of ethene (MO 6, energy = -0.39228a.u.). Corresponds to π_1s from Fig 2.

For Figures 3, 4, and 5, only the MOs that would be directly relevant from the frontier orbitals are shown. It can be obviously seen that the frontier orbital theory is sufficient for this case - MO 16 and MO 18 cannot be generated from the HOMO and LUMO of the reactants only. A more correct interpretatin and diagram is depicted in Figure 2. In addition, it is clear the symmetry of the orbitals are important for their interaction and for a reaction to proceed - with orbitals only interacting with each other if they have the same symmetry. This can be formalized by the orbital overlap integral:

$S_{A B} = < ψ_{A}^{*} | ψ_{B} >$

where $S_{A B}$ is the overlap integral for wavefunctions A and B, $ψ_{A}^{*}$ is the Hermitian adjoint of wavefunction A, and $ψ_{B}$ is wavefunction B. It is immediately evident that where $ψ_{A}$ and $ψ_{B}$ are of opposite phase, $ψ_{A} \times ψ_{B}$ is an odd function and $S_{A B}$ evaluates to 0. Specifically:

the overlap integral is zero for a symmetric-antisymmetric interaction;
the overlap integral is non-zero for a symmetric-symmetric interaction; and
the overlap integral is non-zero for a antisymmetric-antisymmetric interaction.

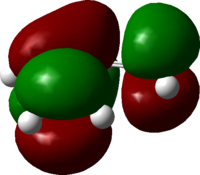
The transition state for this reaction could be quite easily found as it is a simple molecular system. As detailed above, it was verified to be correct as it contains only 1 imaginary frequency, and the vibration corresponds to the desired reaction path. The transition state is visualized below.

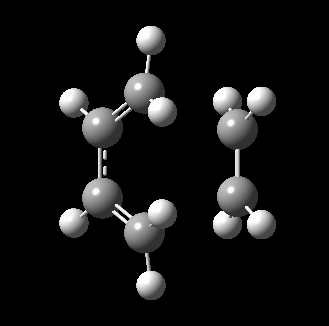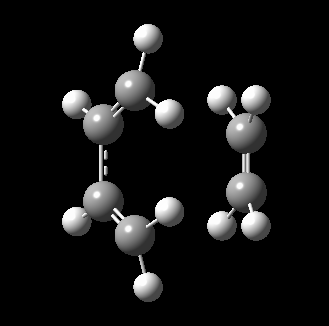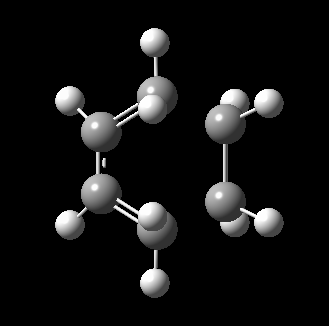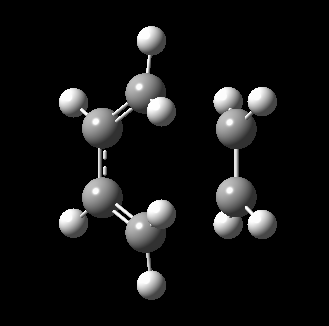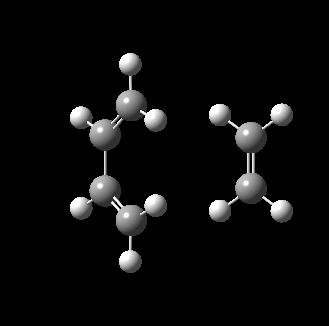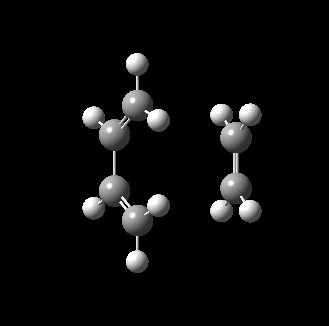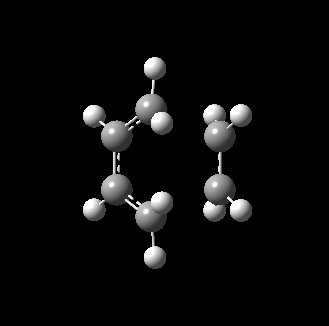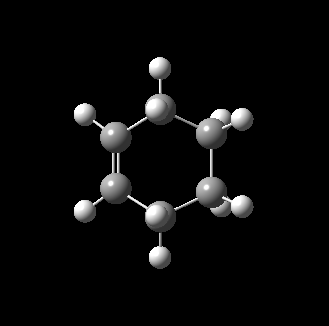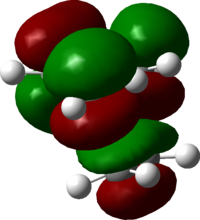
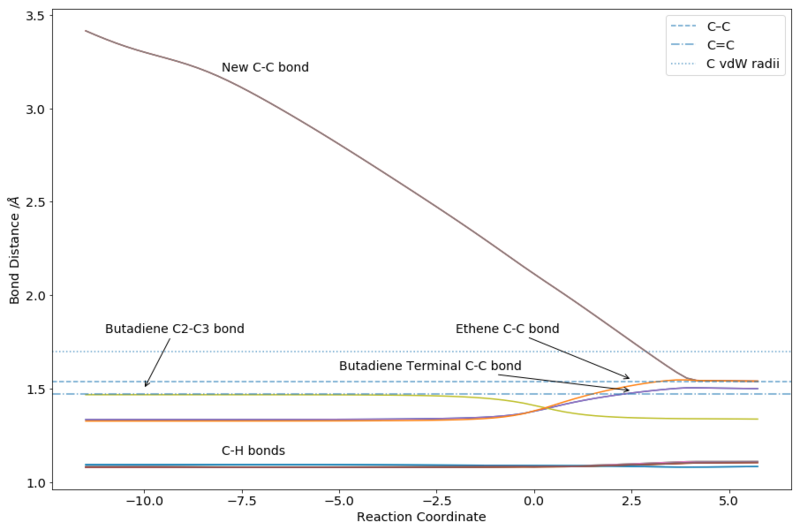
**Figure 6a**: Transition state vibration at 948.67i cm^-1. Calculated E(RPM6] = 0.11286018 at ultrafine grid.

**Figure 6b**: IRC path for reaction between buta-1,3-diene and ethene.

From the transition, an IRC optimization was carried out to find the reaction path, and to confirm that the transition state is indeed the transition state. The IRC path is also shown above, illustrating the correct TS and transition state is found. The changes to the bond lengths of the products and reactants could be visualized from the IRC.

|

|

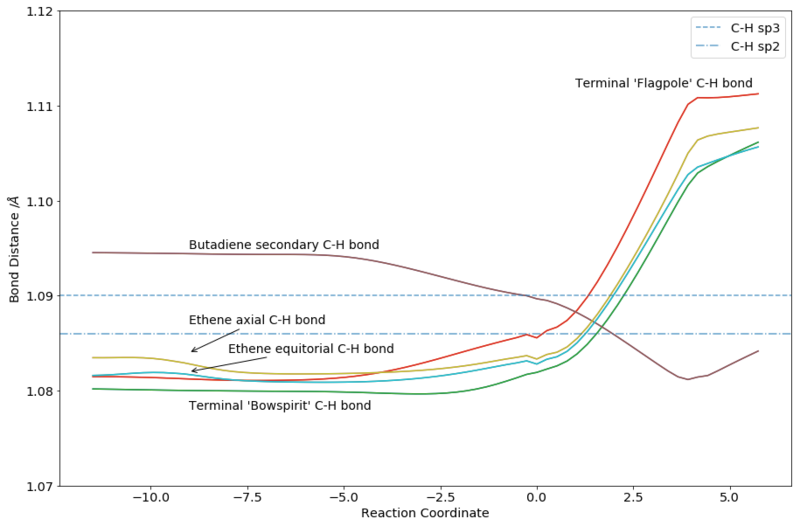
As can be seen from Figure 7, the bond lengths of the various C-C and C-H bonds vary across the reaction coordinate as expected. In general, variation comes from the change in hybridization of the terminal carbons bonds on butadiene and ethene from double bond to single bond, and the change from 'middle' carbons on butadiene from single to double bond. Similar variations are seen for C-H bonds, although the trend is not as straightforward. Notably, differences in the products are seen depending on the position of the hydrogen - axial vs equitorial, bowspirit vs flagpole. The two forming C-C bonds could also be seen approaching each other over time.

From the animation as well as the overlapped nature of the graph (each line has another line underneath), it is clear that the formation of the two bonds was synchronous. This was to be expected as the reactants, transition state and product all have the same plane of symmetry.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

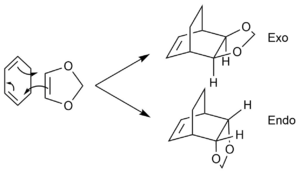
The reaction is another example of a Diels-Alder reaction. Changing the dienenophile from ethene to dioxole allowed the possibility of the product having two stereoisomers - the endo product and the exo product. The IRC paths for the respective products are as follow:

**Figure 9a**: IRC path for the reaction between cyclohexadiene and 1,3-dioxole with the exo product.

From Figure 9, it could be seen that the transition state leading to the different products had different transition structures. The reactants' MO should however be identical:

Cyclohexadiene

1,3-Dioxole

LUMO

MO 23, energy = -0.01710 a.u., antisymmetric

MO 20, energy = +0.03794 a.u., symmetric

HOMO

MO 22, energy = -0.20551 a.u., symmetric

MO 19, energy = -0.19594 a.u., antisymmetric

From the molecular orbitals of the reactants, the transition state MO could be inferred. As with the previous section, only orbitals with the same symmetry have significant interactions. The reactant molecules overlap in either an endo or exo orientation. The molecular orbitals of the transition state is visualized as below:

Endo Transition State

Exo Transition State

LUMO +1 (MO43)

energy = +0.01550 a.u., antisymmetric

energy = +0.01024 a.u., antisymmetric

LUMO (MO42)

energy = -0.00466 a.u., symmetric

energy = -0.00703 a.u., symmetric

HOMO (MO41)

energy = -0.19047 a.u., symmetric

energy = -0.18561 a.u., symmetric

HOMO-1 (MO40)

energy = -0.19650 a.u., antisymmetric

energy = -0.19803 a.u., antisymmetric

The relevant endo and exo TS MOs show similar characteristics, with the exception of the HOMO. For the endo TS, in addition to the normal overlap between the reacting carbons as shown on the exo TS, there were secondary orbital overlaps between the oxygen with the middle two carbon atoms of the diene. This stabilizes the interactions, lowering the overall TS energy. In addition, additional repulsive non-covation interactions (i.e. steric clash) can be seen in the exo transition state. The energy difference can be seen in the energy profile of the reaction as below:

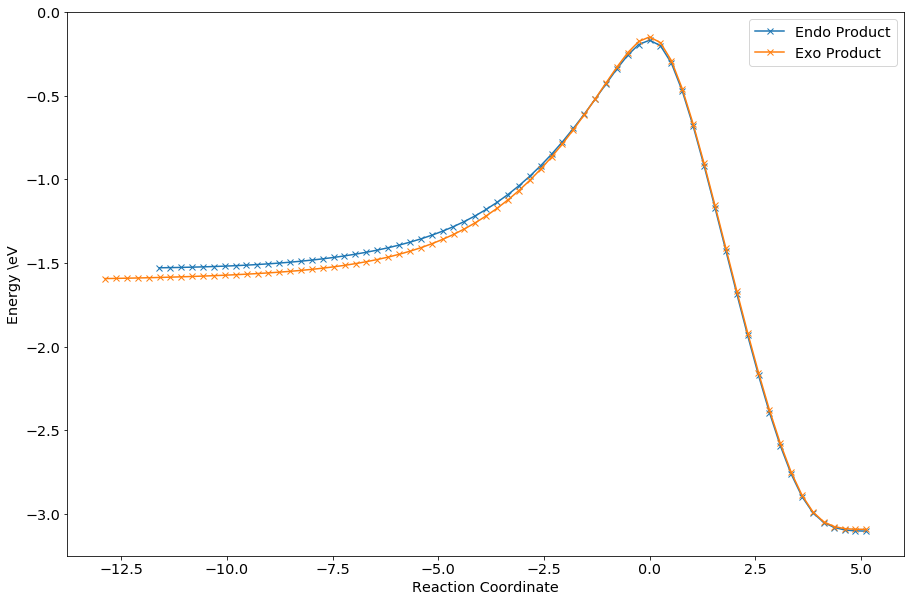
**Figure 10**: Energy profile of the reaction over the IRC path. Reactants on the left.

From the reaction profile, it could be seen that the endo pathway has slightly lower energy at transition state, as discussed above. According to the Arrhenius equation, $k = A e^{\frac{- E_{a}}{R T}}$ , a lower activation energy would lend to a fastor rate of reaction, thus the endo product would be formed preferentially. However, it is noted that the endo product has a lower energy than the exo product - this would imply that the endo product is thermodynamically more stable. This is the opposite of what was expected - the exo product is usually the more thermodynamically stable one due to the steric clash present in the endo product. In this case, steric clash is seen in both products. The thermodynamics of the reaction was calculated using B3LYP/6-31G(d) and is given below. The results correspond with what was seen from PM6 above.

	Cyclohexadiene	Dioxole	Sum of Reactants	Endo TS	Exo TS	Endo Product	Exo Product
$Δ G^{o}$ /kJ mol^-1	-612591	-701188	-1313780	-1313622	-1313614	-1313849	-1313845

	Reaction Energy /kJ mol^-1	Reaction Barrier /kJ mol^-1
Endo	-69	+158
Exo	-65	+166

Using results from the MO calculations, a MO diagram for the formation of the TS could be plotted. As previously mentioned, only orbitals of the same symmetry can interact with each other.

From the MO diagrams, it can be seen that the dienenopphile, 1,3-dioxole, has a HOMO of a higher energy due to electron donation by the oxygens. This reaction is thus an inverse-demand Diels-Alder reaction.

(Fv611 (talk) Your MO diagrams are correct but they do not have proper labelling. You also should have inserted your calculation .LOG files.)

You have come to the correct conclusions but your discussion is quite brief and you have missed out a few things such as what si the electron demand of the reaction. Your theory section was excellent and you have clearly put in loads of effort. You just should have followed the script more.

Exercise 3: Diels-Alder vs Cheletropic

The reaction between o-xylylene and SO₂ form two different types of bicyclic products - a Diels-Alder product with two six-membered rings, and a cheletropic product with one six-membered ring and one five-membered ring:

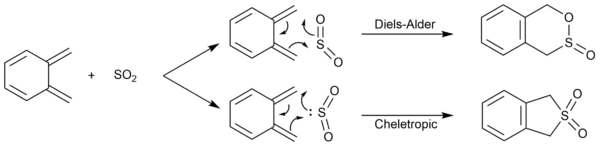
The hallmark of a chelotropic reaction is both bond form reactions happen on the same atom. In this case, both bond formation occur on the sulphur atom. Together with the two stereoisomers from the Diels-Alder reaction, a total of 3 products could be obtained with 3 different reaction paths:

Figure 13a: IRC path for the Diels-Alder reaction resulting in the exo product.	Figure 13b: IRC path for the Diels-Alder reaction resulting in the endo product.
Figure 13c: IRC path for the cheletropic reaction.

From the IRC animation, it could be seen that the new bonds are formed asynchronously. This is due to the lack of the mirror plane, as could be found in the previous two exercises. However, as symmetry was maintained in the cheletropic reaction, the bonds were formed synchronously.

The energy along the reaction path could be followed in a similar manner:

(The problem with overlaying IRCs is that they don't exist in the same reference frame. The reaction coordinate is different for all three. Another issue is the IRC gives you the electronic energy when we want the free energies of the stationary points. However it's ok to get a qualitative comparison of the three. Tam10 (talk) 15:14, 16 March 2018 (UTC))

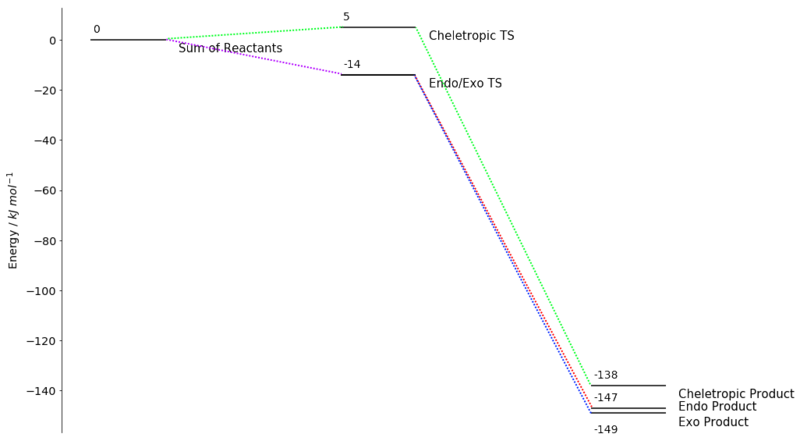
While PM6 was not able to give accurate results for the reactant and product energies, the overall trend in the reactions was clear. As with other Diels-Alder reactions investigated above, the endo TS showed a slightly energy than the exo TS, making the endo TS the kinetic product. The cheletropic product showed significantly higher transition state energies, and may not be readily observed. More accurate results were obtained using B3LYP/6-31G(d):

	o-xylylene	SO₂	Sum of Reactants	Endo TS	Exo TS	Cheletropic TS	Endo Product	Exo Product	Cheletropic Product
$Δ G^{o}$ /kJ mol^-1	-812870	-1440316	-2253186	-2253200	-2253200	-2253181	-2253333	-2253335	-2253324

	Reaction Energy /kJ mol^-1	Reaction Barrier /kJ mol^-1
Endo	-147	-14
Exo	-149	-14
Cheletropic	-138	+5

(You should definitely not be getting negative barriers! There must be a minimum in between your reactants and TS, or, more likely, your SO2 energy is wrong Tam10 (talk) 15:14, 16 March 2018 (UTC))

Calculation using B3LYP/6-31G(d) show different trend as compared to PM6 previously. The energy TS for the endo and exo products are essentially identical, possibly owing to minimal sterics and interaction due to the small SO₂ size. In addition, they appear below the energy of the reactants. This could be a quirk of the optimization or due to the aromatization energy. However, as expected, the exo product is the most thermodynamic product, with the cheletropic pathway being quite unfavourable. The generated reaction profile is as follow:

The Other Diels-Alder Reaction

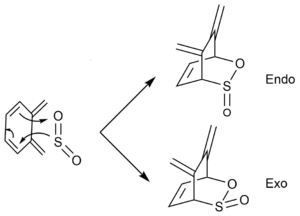
The Diels-Alder reaction could also take place at the other pair (non-terminal) of diene to form another two (exo and endo) products. The reactions proceed as below:

**Figure 17a**: IRC path for the *other* Diels-Alder reaction resulting in the exo product.

**Figure 17b**: IRC path for the *other* Diels-Alder reaction resulting in the endo product.

Due to the loss of the free energy of aromatization in this reaction, the reaction was expected to be much more unfavourable. The energy from IRC was plotted and compared to the normal positions above:

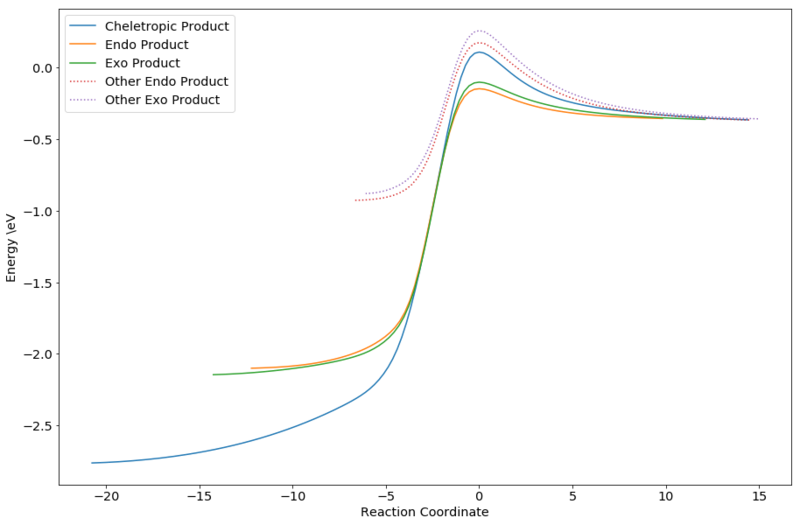
From the graph, it could be clearly seen that the Diels-Alder reactions at the non-terminal dienes are kinetically much less favourable. Due to the loss in aromaticity, the products are also less thermodynamically stable. As such, Diels-Alder reactions would not happen at this position.

Conclusion

Some examples of Diels-Alder reactions were investigated in this experiment. The reaction proceed in a single step with a single transition state, without intermediates. In general, the bond-forming reaction proceed in a synchronous manner. The reaction barrier for the reaction may be reduced through secondary orbital interactions, preferring endo products over exo products where secondary orbital interactions are possible. Additional interactions, such as sterics or aromatization may also promote specific regio or stereoisomers of the Diels-Alder product. The cheletropic reaction was also investigated, and was found to have higher reaction barrier, but produces more stable 5-membered adduct.

References

↑ E. Lewars, Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Springer Netherlands, Dordrecht, 2nd edn., 2011.
↑ E. Lewars, Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Springer Netherlands, Dordrecht, 2nd edn., 2011.

[1] E. Lewars, Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Springer Netherlands, Dordrecht, 2nd edn., 2011.

[2] E. Lewars, Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Springer Netherlands, Dordrecht, 2nd edn., 2011.

[1]

[2]