Rep:MOD:RHL8964

Introduction:

PES: During a calculation by Gaussian, the program calculates the energy under the principle of Born-Oppenheimer Approximation for every structure generated by changing any degree of freedom available. As the program condense that 3N-6 degrees of freedom down to 3, we obtain the potential energy surface (PES).

Nf710 (talk) 10:56, 4 November 2016 (UTC) (good understanding, its not actually a surface but a 3n-6 varying vector space wrt. energy)

Minimum: Across the potential energy surface we have peaks and troughs, stationary points which represents the maximums and minimums of energy. We can easily obtain the minimums by optimising the molecular structure, during which the program would go down the potential energy surface along the steepest slope based on the predicted structure given until reaching the point where it can't find a negative slope all around the place. The gradient at this minimum will be absolutely zero but the curvature will be the most positive value locally, if not globally because the surface is just about to rise up again.

The problem is that the minimum we obtain from optimisation could only be a local minimum rather than the global minimum because the slope in the given prediction could only lead to one more ''shallow'' minimum.

Transition State: The transition state is where we find the gradient equals zero but the curvature to be negative at one direction, just like the middle of a saddle. In another word, the transition state is the highest point on the pathway from one minimum to another minimum. The least steepest slopes connecting one minimum to another will be connected to form the reaction pathway and the transition state sits on the top of the pathway. (1)

Exercise I: Reaction of Butadiene with Ethylene

MOs:

Reactant/TS	Orbital	Symmetry
Ethylene	HOMO	u
Ethylene	LUMO	g
Butadiene	HOMO	g
Butadiene	LUMO	u
TS	2nd HOMO	N/A
TS	HOMO	N/A
TS	LUMO	N/A
TS	2nd LUMO	N/A

The visualisation of the HOMO and LUMO of TS demonstrated that they were formed by the interaction between the HOMO of ethylene and the LUMO of butadiene (normal electron demand). The remaining two orbitals, the LUMO of ethylene and the HOMO of butadiene interacted more weakly and formed the 2nd LUMO and 2nd HOMO of the transition state. The strong interaction between orbitals of the same symmetry rather than those of different symmetries showed that the orbital overlapping integral was non-zero, if not 1, only when the interacting orbitals were of the same symmetry.

Nf710 (talk) 11:12, 4 November 2016 (UTC) (The overlap integral would only be 1 if the orbital where the same, this is due to the orthonormality of the basis sets.)

Changes in bond lengths:

	Ethylene	Butadiene	Transition State	Product
Compound
Bond length (Å)	C=C: 1.327	C1C2=C3C4=1.335 C2C3=1.468	C1C2= 1.382 C3C4=C5C6=1.380 C4C5=1.411 C1C6=C2C3=2.114	C1C6=1.338 C1C2=C5C6=1.500 C2C3=C4C5=1.540 C3C4=1.541

The C=C bonds in both the ethylene and butadiene are extended in the transition state and eventually become single bond.

The C-C single bond in butadiene shrinks in the transition state and eventually becomes a C=C double bond.

The terminal carbons of both molecules slowly reach each other and form single bonds.

The C-C single bonds formed in the final products all have the expected lengths, c.f. C-C sp3-sp3= 154 pm and C-C sp3-sp2= 150 pm). The double bond formed in the final product is slightly shorter than the C=C bond length in ethylene but much shorter than the theoretical estimation (147 pm) (2).

The Van der Waals radius of carbon is 170 pm (3), which means that during the transition states, the carbons at reaction centres are closer in distance than the Van der Waals radius for the reaction to proceed.

Vibration:

Imaginary Frequency	Lowest Positive Frequency

The imaginary frequency, which shows the vibration that leads to the transition state (1), consists of several different components. It involves the stretching of C=C and shortening of C-C bonds in both reactants, which follows the exact trend we see from the changes in bond lengths from reactants to the final product. The vibration also consists of in- and out-of-plane bending of the reacting centres, which are the two carbons in ethene and the terminal carbons in butadiene. The reacting centres approach each other in the vibration and this hence leads to the reaction taking place.

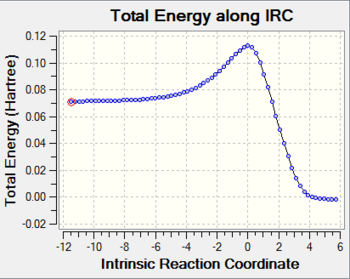
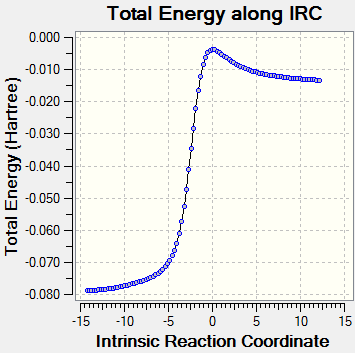
IRC:

Pathway Animated	Energy

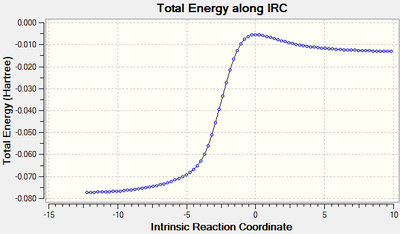
The animation from IRC calculation shows a mostly synchronous reaction. The two bonds form almost at the same time.

The concerted reaction is further supported by the fact that there is only one energy maximum in the entire pathway, as shown in the graph attached.

Nf710 (talk) 11:28, 4 November 2016 (UTC) (Good analysis here, You could have put an MO diagram in, good explanation of the VdW radius in the transition state and also discussion of the synchronous nature of the reaction.)

Exercise II: Reaction of benzoquinone with cyclopentadiene

MOs:

		Product
Endo	HOMO
	LUMO
Exo	HOMO
	LUMO	(You need to give unique names for every image uploaded! You have overwritten your own TS images as well as the images of other wikis Tam10 (talk) 17:21, 27 October 2016 (BST))

As shown in the MOs above, the HOMO of the cyclopentadiene interacts with the LUMO of benzoquinone, which are in the same gerade phase, in forming the final DA product. Since the reaction involves the interaction between the HOMO of diene and the LUMO of dienophile, we can say this reaction is of normal electron demand. In this reaction, the two carbonyl groups effectively withdraw electron density from the C=C double bond on the benzoquinone and hence reduce the energy of the C=C bond, making benzoquinone a good dienophile.

(Good paragraph here, you've brought together all the important points Tam10 (talk) 17:21, 27 October 2016 (BST))

Energies:

unit: kJ/mol	Cp	Benzoquinone	TS	Product	Activation energy	Reaction energy
Endo	-194.034782	-381.396835	-575.399596	-575.442366	0.032021	0.010749
Exo	-194.034782	-381.396835	-575.397171	-575.442094	0.034446	0.010477

(You've written kJ/mol but you haven't actually converted energies Tam10 (talk) 17:21, 27 October 2016 (BST))

The endo product is the kinetic product of the reaction due to its lower activation barrier; the exo product is the thermodynamic product since it has a higher reaction energy.

(But you've shown in the table the endo has a larger reaction energy! Endo is in face the thermo product too Tam10 (talk) 17:21, 27 October 2016 (BST))

Nf710 (talk) 11:41, 4 November 2016 (UTC) (Your energies are incorrect, I suspect you havent used the correct basis set specified and therefore your not getting the ones we expect. However that being said your results you results still show the correct trend, which means they are still valid results.)

Secondary orbital interactions and steric clashes:

If we compare the HOMOs of the two transition states, we can see that the newly forming pi system on the Cp ring can potentially interact with the pi* system on the unreacted C=C double bond, establishing a significant secondary orbital interaction. This secondary interaction can effectively reduce the activation energy of the reaction and make the endo product the kinetically favoured product.

Although the secondary orbital interaction reduces the energy of the transition state, it is inevitable that the approaching Cp and benzoquinone ring will clash and hence increase the energy of the final product. Therefore, the exo product, which is free of any steric clashes, is the thermodynamically favoured product.

Nf710 (talk) 11:45, 4 November 2016 (UTC)(your argument for the thermodynamic product is wrong because you are contradicting your results. But your secondary orbital overlap is good.)

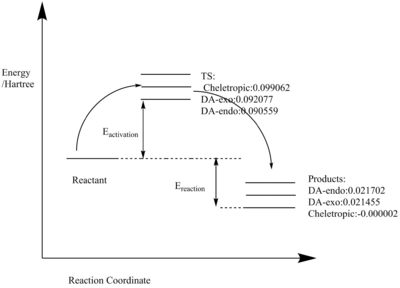
Exercise III: Diels-Alder vs cheletropic

Energies:

Unit:Hartree	Xylylene	SO2	TS	Product	Activation barrier	Reaction energy
DA- exo	0.090563	-0.118614	0.092077	0.021455	0.120128	0.049506
DA- endo	0.090563	-0.118614	0.090559	0.021702	0.11861	0.049753
Cheletropic	0.090563	-0.118614	0.099062	-0.000002	0.127113	0.028049

Among the three pathways, the endo product of DA reaction had the lowest activation barrier which was the kinetically preferred product.

The Cheletropic product, though having the highest activation barrier, has the lowest reaction energy, which made the cheletropic product the thermodynamically preferred product.

(Yes. Again, convert units to kJ/mol Tam10 (talk) 17:21, 27 October 2016 (BST))

IRC:

	IRC	Pathway
DA-exo
EA-endo
Cheletropic

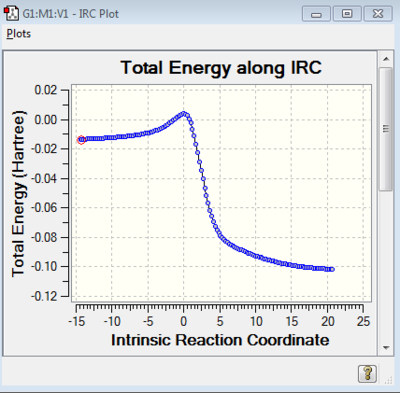
The first two IRC animation obtained showed reversed processes to the reactions while the third showed a normal pathway.

During the lab sessions it was proposed that changing the direction of IRC calculation might yield a normal pathway, but the result showed incomplete optimisation and unconverged energies.

This might be due to the fact that this specific transition state had a steeper slope towards the reactant but a less steeper one to the product, which would easily fall back to the reactant if no other limitation was put in place.

(Don't worry about this - Gaussian doesn't know which way around the reactants and products are Tam10 (talk) 17:21, 27 October 2016 (BST))

Structural Change in Xylylene:

The xylylene experienced significant structural changes during the reaction. Both processes involved the delocalisation of pi electrons into the hexadiene ring, and during the reaction the pi electrons inside the six-member ring would gradually delocalise while the bond lengths of the newly forming C=C bond and the previous C-C single bonds would shorten.

Reaction Profile:

Conclusion

In this computational lab, 3 mechanisms were studied using Gaussian. The reactants were optimised before being placed in guessed transition state positions to be optimised into transition states. The optimised transition states were used to perform IRC calculations which provided valuable insight into the reaction mechanism. The HOMO-LUMO interactions between reactants could be studied by generating simulated MOs and details of the reaction such as electron demand, steric clashes and secondary orbital interactions could be obtained.

For most of time, with reasonable approximations and right choice of calculation method, the program could yield promising simulation results; however, the complexity of quantum mechanics and computing inevitably made the entire process prone to mistakes and it was rather hard to be fixed. Some efforts were put to solving these issues but the result was far less satisfying.

Reference:

(1) Lecture notes: Quantum Mechanics 3/3rd Year Computational Chemistry, Michael Bearpark, Imperial College London

(2) https://en.wikipedia.org/wiki/Bond_length

(3) http://periodictable.com/Properties/A/VanDerWaalsRadius.v.html

(4) http://www.cup.uni-muenchen.de/ch/compchem/vib/thermo1.html