Rep:MOD:Niyi
Module 3
The aiming of this module is to characterise the transition states for both the Cope Rearrangement and Diels-Alder cycloaddtion reactions, with mapping their structures on potential energy surfaces. Since the molecules are larger, molecular orbital-based methods need to be used to solve the Schrodinger equation and locate the transition structures.
The Cope Rearrangement Reaction
This part aims to determine the low-energy minima and transiton state structure of 1, 5-hexadiene during its concerted [3,3]-sigmatropic rearrangement reaction, which is called Cope Rearrangement.
Then, the preferred mechanism can be found by analyzing the energy in both “chair” transition state and “boat” transition state, where the “boat” transition structure is normally higher in energy.

Optimisation of the Reactants:1, 5-Hexadiene
Anti Conformer
Firstly, a molecule of 1, 5-hexadiene with an antiperiplanar conformation is drawn and cleaned in Gaussview. Then this conformer is optimized using HF/3-21G level of theory with 250 MB memory limit.
Optimised Anti Conformer
test molecule |
General Information
| Point Group | Ci |
| Energy | -231.69254 a.u. |
When compared to the energy of the reference[1], this anti conformer is identified to have an anti2 structure. Moreover, it has identical energy to the referenced anti2 conformer.
Real Output of Optimised Anti Conformer
Item Value Threshold Converged?
Maximum Force 0.000022 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000923 0.001800 YES
RMS Displacement 0.000380 0.001200 YES
Predicted change in Energy=-6.506594D-09
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
File Link
The optimisation file is liked to here
Frequency Analysis
Then a frequency analysis is carried out using the optimisation file. By ensuring there are no imaginary frequencies, the structure is confirmed to be optimised to a minimum.
File Link
The frequency analysis file is liked to here
Gauche Conformer
A molecule of 1, 5-hexadiene with a gauche conformation is drawn and cleaned in Gaussview. Then the conformer is optimized using HF/3-21G level of theory with 250 MB memory limit.
Optimised Gauche2 Conformer
test molecule |
General Information
| Point Group | C2 |
| Energy | -231.69167 a.u. |
When compared to the energy of the reference[1], this gauche conformer is identified to have an gauche2 structure.
The energy of gauche2 is higher than that obtained from the anti conformer.
Real Output of Optimised Gauche2 Conformer
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000174 0.001800 YES
RMS Displacement 0.000055 0.001200 YES
Predicted change in Energy=-2.478246D-09
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
File Link
The optimisation file is liked to here
Optimised Gauche3 Conformer
test molecule |
General Information
| Point Group | C1 |
| Energy | -231.69266 a.u. |
When compared to the energy of the reference[1], this anti conformer is identified to have an gauche3 structure. It has the lowest energy in all the conformers.
Real Output of Optimised Gauche3 Conformer
Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.001218 0.001800 YES RMS Displacement 0.000326 0.001200 YES Predicted change in Energy=-2.568487D-08 Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
File Link
The optimisation file is liked to here
Analysis of the lowest energy conformation
Usually, the anti conformor is predicted to be lower in energy since the orbital overlapping effect dominates in the alkyl molecules. This is mainly due to the anti-periplanar arrangement which allows the molecule to experience less steric interactions.
However in this case, the gauche3 conformer is found to have lower energy. This may results from some elelctronic interactions (e.g. Van der Waals’ attractions between H atoms) or the stabilizing effect caused by pi-pi orbital overlap. Also, this may result from calculating using a lower level of theory.
Anti2 Conformer Using B3LYP/6-31G* Level of Theory
A Ci anti2 conformation of 1, 5-hexadiene is drawn previously, thus it is optimized at the B3LYP/6-31G* level of theory.
Optimised Anti2 Conformer
test molecule |
General Information
| Point Group | C2h |
| Energy | -234.61171 a.u. |
When B3LYP/6-31G* level of theory is used, the point group changes from Ci to C2h.
Real Output of Optimised Anti2 Conformer
Item Value Threshold Converged?
Maximum Force 0.000016 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.000262 0.001800 YES
RMS Displacement 0.000089 0.001200 YES
Predicted change in Energy=-1.681679D-08
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
File Link
The optimisation file is liked to here
Frequency Analysis
Then a frequency analysis is carried out using the optimisation file. By ensuring there are no imaginary frequencies, the structure is confirmed to be optimised to a minimum.
File Link
The frequency analysis file is liked to here
IR spectrum of the Anti2 Conformer
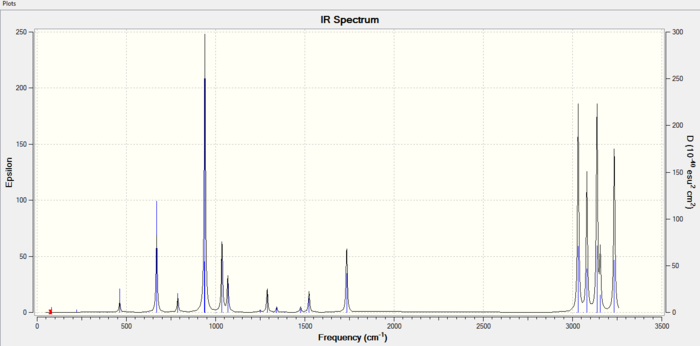
Thermochemistry
From the data obtained from the Gaussian output, we can get information as below,
1) Sum of electronic and zero-point Energies= -234.469204 (the potential energy at 0K including the zero-point vibrational energy)
2) Sum of electronic and thermal Energies= -234.461857 (the energy at 298.15 K and 1 atom of pressure which includes the translational, rotational and vibrational energy modes)
3) Sum of electronic and thermal Enthalpies= -234.460913 (contains an additional correction for RT)
4) Sum of electronic and thermal Free Energies= -234.500777 (includes the entropic contribution to the free energy)
Comments
| HF/3-21G | B3LYP/6-31G* | |
|---|---|---|
| C=C | 1.33352Å | 1.31613Å |
| C-C | 1.54808Å | 1.55294Å |
| Dihedral Angle | -179.963 ° | 180.000° |
The bond length of the carbon-carbon double bond is shortened, whereas the bond length of the carbon-carbon single bond is lengthened for the B3LYP/6-31G* calculation. Moreover, the dihedral angle of the central C-C-C-C also becomes different and exactly equals to 180°.
The B3LYP/6-31G* method has a better basis set than the HF/3-21G method, and thus gives a better optimization for the structures. Therefore, the results obtained from it would have a closer value to the experimental measurements.
Moreover, 1, 5-hexadiene has a small value of dipole moment because the electronegativity difference between the carbon atom and hydrogen atom is small.
Optimisation of the Chair/Boat Transition Structure
The chair transition structure for the Cope rearrangement consists of two C3H5 allyl fragments at nearly 2.2Å apart with C2h symmetry, whereas the boat transition structure is made of the same fragments but with C2v symmetry. By guessing the chair and the boat transition states, the transiton structure for the Cope Rearrange reaction could be found.
Optimisation of Allyl Fragment
An allyl fragment is optimized at HF/3-21G level of theory, then this optimized fragment is copied and pasted twice in order to rearrange it into a chair transition state for the Cope Rearrangement of 1, 5-hexadiene since it is a half of the both transition structures.
Optimised Allyl Fragment
test molecule |
General Information
| Point Group | C2v |
| Energy | -115.82304 a.u. |
Real Output of Optimised Allyl Fragment
Item Value Threshold Converged? Maximum Force 0.000048 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.000141 0.001800 YES RMS Displacement 0.000070 0.001200 YES Predicted change in Energy=-1.277266D-08 Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
File Link
The optimisation file is liked to here
Optimisation of Chair Transiton Structures
The distance between one terminal end of the allyl fragment is 2.20209Å, the other one is 2.19491Å. Then two different methods are used to optimize this transition state. In the first one, it is assumed to have a reasonable guess transition structure which allows the program to compute the Hessian and then the optimisation process proceeds. If the guess structure defers a lot from the exact structure, the reaction coordinate needs to be frozen and the rest of molecule is minimised. Once the process is complete, the coordinate could be unfrozen and then the whole molecule is being optimised again.
Guess Chair Transition Structure-Force Constant Matrix
The molecule is optimized with frequencies calculated, choosing optimization to a TS(Benny), calculating the force constants once and additional words Opt=No Eigen. The word NoEigen allows to preventing the calculation from clashing when more than one imaginary frequency is found during the process. The optimization ends to give a structure as below, which has an imaginary frequency of magnitude, which corresponds to the Cope rearrangement.
Optimised Guess Chair Transition Structure
test molecule |
General Information
| Point Group | C2h |
| Energy | -231.61932 a.u. |
| Bond Breaking/Making Distance | 2.02126Å |
Real Output of Optimised Guess Chair Transition Structure
Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000829 0.001800 YES RMS Displacement 0.000115 0.001200 YES Predicted change in Energy=-7.523575D-08 Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
The optimization ends to give a structure as above, which has an imaginary frequency of magnitude -817.98 cm-1, which corresponds to the Cope rearrangement. The animation of this vibration is shown below,
File Link
The optimisation file is liked to here
Guess Chair Transition Structure-Frozen Coordinate
Then the guess transition structure is calculated with HF/3-21G level of theory using frozen coordinate method by fixing the forming bonds and thus minimizing all other degrees of freedom.
Optimised Guess Chair Transition Structure
test molecule |
General Information
| Point Group | C2h |
| Energy | -231.61525 a.u. |
| Bond Breaking/Making Distance | 2.19491Å |
Since the program fails when the bond distance is fixed to 2Å, thus in this calculation just the coordinate is frozen but the bond length is the same to the input file.
Real Output of Optimised Guess Chair Transition Structure
Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000742 0.001800 YES RMS Displacement 0.000146 0.001200 YES Predicted change in Energy=-1.837538D-08 Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
File Link
The optimisation file is liked to here
Then by changing the frozen bonds to derivative, the structure is reoptimised using a normal guess Hessian to a transition state as before without calculating the force constants.
Optimisation of Boat Transition Structure
QST2 Transition Optimization Method is used to optimize the boat transition structure and it allows to specifying the reactants and products for the cope rearrangement reaction. Moreover, this method interpolates between two minima in order to find the transition state.
In this case, the atom should be labeled differently although the reactants and products are identical in structure which corresponds to the anti2 conformer of 1, 5-hexadiene.
An Opt+Freq job is carried out with optimisation to a transition state TS(QST2), which corresponds to a QST2 calculation.
However, the optimization calculation using the QST2 method failed to give the boat transition state, but giving a dissociated chair transition state. Therefore, the structure of both reactants and products need to be adjusted as below.

Then an optimization calculation using QST2 method is carried out again, which gives a successful boat transition structure.
Optimised Boat Transition Structure
test molecule |
General Information
| Point Group | C2v |
| Energy | -231.60280 a.u. |
Real Output of Optimised Boat Transition Structure
Item Value Threshold Converged? Maximum Force 0.000095 0.000450 YES RMS Force 0.000025 0.000300 YES Maximum Displacement 0.001366 0.001800 YES RMS Displacement 0.000403 0.001200 YES Predicted change in Energy=-2.718903D-07 Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
An imaginary frequency is found at -840.23 cm-1, which corresponds to the Cope rearrangement. The animation of this vibration is the same as what we have obtained for the chair transition state and is shown below,
File Link
The optimisation file is liked to here
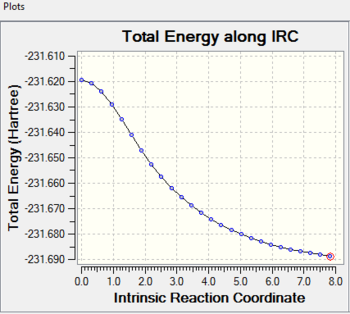
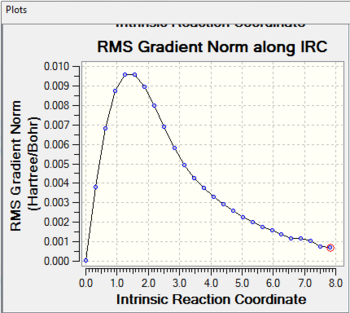
Intrinsic Reaction Coordinate
It is impossible to determine which conformers of 1,5-hexadiene would link to the optimized chair and boat transition structure. Thus the Instrinsic Reaction Coordinate(IRC) method is used to follow the minimum energy pathway on the potential energy surface from the transiton state to the local minima(which corresponds to the reactants or the products).
The optimized guess chair transition state (calculating with force constant matrix) is used to carry out the IRC calculation with the HF/3-21G level of theory. The calculation is run in only one direction as the reaction coordinate is symmetrical. Then the force constant is chosen to be calculated once at every step along the IRC and the number of points along the IRC is set to be 50.
General Information
| Energy | -231.68862 a.u. |
| RMS Gradient Norm | 0.00072241 |
When the calculation completes, less steps are completed than what is required as before. Although the optimization is successful, a minimum geometry has not been reached. The general information of the last point on the IRC is shown above.
File Link
The optimisation file is liked to here
Further Attempts
Three options can be done in order to get a minimum geometry: 1) Take the last point on the IRC and optimize it to a minimum 2) Restart the IRC and increase the number of steps 3) Redo the IRC with computing the force constants at every step
| Option | Energy | Structure | File Link |
|---|---|---|---|
| Optimisation of last point | -231.69167 a.u. |  |
here |
| IRC with 100 steps | -231.68862 a.u. |  |
here |
| IRC with 150 steps | -231.68862 a.u. |  |
here |
| Force constant computed at every step | -231.66560 a.u. |  |
here |
From the data obtained above, attempt 1 is the most successful one and the result converges to a Gauche 2 structure.
Activation Energies
To calculate the activation energies, an optimisation calculation and a frequency calculation are needed to be carried out for both transition structures. The calculation could be started based on the previous HF/3-21G optimised structures using the B3LYP/6-31G* level of theory.
Reoptimisation of Chair Transition State
Optimised Chair Transition State
test molecule |
General Information
| Energy | -234.55698 a.u. |
Real Output of Optimised Chair Transition State
Item Value Threshold Converged?
Maximum Force 0.000018 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.001381 0.001800 YES
RMS Displacement 0.000257 0.001200 YES
Predicted change in Energy=-1.080636D-07
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
File Link
The optimisation file is liked to here
Frequency Analysis
The frequency analysis is carried out using the previous file with a B3LYP/6-31G* level of theory.
General Information
| Energy | -234.55698 a.u. |
The energy is the same as that obtained from optimisation calculation. An imaginary frequency is observed at -565.72 cm-1, and the animation of this vibration is shown below.
Thermochemistry
Sum of electronic and zero-point Energies= -234.414931
Sum of electronic and thermal Energies= -234.409010
Sum of electronic and thermal Enthalpies= -234.408066
Sum of electronic and thermal Free Energies= -234.443817
File Link
The optimisation file is liked to here
Reoptimisation of Boat Transition State
Optimised Boat Transition State
test molecule |
General Information
| Energy | -234.54309 a.u. |
Real Output of Optimised Boat Transition State
Item Value Threshold Converged?
Maximum Force 0.000304 0.000450 YES
RMS Force 0.000074 0.000300 YES
Maximum Displacement 0.001756 0.001800 YES
RMS Displacement 0.000780 0.001200 YES
Predicted change in Energy=-1.694834D-06
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
File Link
The optimisation file is liked to here
Frequency Analysis
The frequency analysis is carried out using the previous file with a B3LYP/6-31G* level of theory.
General Information
| Energy | -234.54309 a.u. |
The energy is the same as that obtained from optimisation calculation. An imaginary frequency is observed at -531.45 cm-1, and the animation of this vibration is shown below.
Thermochemistry
Sum of electronic and zero-point Energies= -234.402318
Sum of electronic and thermal Energies= -234.395985
Sum of electronic and thermal Enthalpies= -234.395041
Sum of electronic and thermal Free Energies= -234.431729
File Link
The optimisation file is liked to here
Energy Comparisons
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies(at 0 K) | Sum of electronic and thermal energies (at 298.15 K) | Electronic energy | Sum of electronic and zero-point energies(at 0 K) | Sum of electronic and thermal energies (at 298.15 K) | |
| Chair TS | -231.6193224 | -231.466702 | -231.461342 | -234.55698283 | -234.414931 | -234.409010 |
| Boat TS | -231.60280222 | -231.450930 | -231.445302 | -234.54309090 | -234.402318 | -234.395985 |
| Reactant(anti2) | -231.69253529 | -231.539540 | -231.532566 | -234.61171035 | -234.469204 | -234.461857 |
- 1 hartee = 627.509 kcal/mol
| HF/3-21G | B3LYP/6-31G* | Expt | |||
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair TS) | 45.70 | 44.69 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔE (Boat TS) | 55.60 | 54.76 | 41.97 | 44.33 | 44.7 ± 2.0 |
The transition structures show little deviation when calculating using a higher level of theory, but there is a large difference in energies for the same transition structure. When compared with the literature value, the results obtained from the B3LYP/6-31G* calculation show excellent agreement. However, the results obtained from lower level HF/3-21G derive a lot. Since the activation energy of the chair transition structure is shown to be lower than that of the boat transition structure, we can conclude that this Cope Rearrangement reaction would proceed via a chair transition structure.
Diels-Alder Reactions
Diels-Alder reaction is one of the most important pericyclic reactions, which corresponds to a [4+2] cycloaddition reaction between a dieneophile and a diene. During the reaction, the pi orbitals of the diene will interact with the pi orbitals in order to form new sigma bonds. Interactions could either be allowed or forbidden between the frontier orbitals of the dieneophile and the diene. The reaction is allowed if the HOMO of one reactant can interact with the LUMO of the other reactant, whereas the reaction is forbidden when the frontier orbitals have different symmetry and the overlap is poor. (i.e. when there are nodal planes between two reactants)
Usually, the diene is electron rich and the dieneophile is substituted by substituents with pi orbitals that could interact with the new double bond. This would make regiochemistry being stabilized, and the driving force for this reaction would be the formation of two sigma bonds.
In this part, two Diels-Alder reactions are taken into consideration, one of which is the reaction between butadiene and ethylene and the other one the reaction between cyclo-1, 3-diene and maleic anhydride.
Diels-Alder Reaction between Butadiene and Etylene
Optimisation of Cis-Butadiene
A cis-butadiene is optimized using the semi-empirical AM1 level of theory.
Optimised Cis-Butadiene
test molecule |
The structure is appeared to be planar.
General Information
| Point Group | C2v |
| Energy | 0.04879719 a.u. |
Real Output of Optimised Cis-Butadiene
Item Value Threshold Converged?
Maximum Force 0.000030 0.000450 YES
RMS Force 0.000011 0.000300 YES
Maximum Displacement 0.000340 0.001800 YES
RMS Displacement 0.000162 0.001200 YES
Predicted change in Energy=-9.691035D-09
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
| HOMO | LUMO |
|---|---|
 |
|
 |

|
From what we obtain, the HOMO of the cis-butadiene is found to be antisymmetric with respect to the plane and the LUMO is symmetric with respect to the plane.
File Link
The optimisation file is liked to here
Optimisation of Transition State
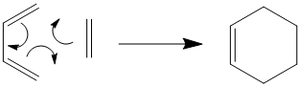
The transition structure for the Diels-Alder reaction is found to have an envelope structure, which could maximize the pi-orbital overlap between the butadiene and the ethylene molecule. A bicycle-octane system is drawn and the –CH2-CH2- fragment is removed in order to build up a guess structure.
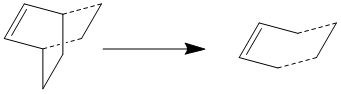
The interfragment distance is set to be 2.2Å and The molecule is optimized using the semi-empirical AM1 level of theory with frequencies calculated, choosing optimization to a TS(Benny), calculating the force constants once and additional words Opt=No Eigen. The word NoEigen allows to preventing the calculation from clashing when more than one imaginary frequency is found during the process.
Optimised Guess Transition State
test molecule |
General Information
| Point Group | Cs |
| Energy | 0.11165468 a.u. |
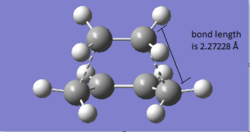
The Geometry of the transition state is shown. From literature, the Van der Waals’ radius is 1.7 Å, a typical sp3 C-C bondlength is about 1.53 Å and a typical sp2 C-C bondlength is about 1.46 Å.The developing sigma C-C bond has a bond length of 2.11945 Å, which is much larger than all these above. This value is smaller than twice of the Van der Waals’ radius for carbon, which implicit a bond being formed. Also, longer than both typical bond lengths indicates that the bond formation process is in progress. Moreover, The bondlength between the two carbons not involved in the reaction is found to be 1.39748 Å. This bond has double bond character since it is shorter than the single C-C bondlength.
Real Output of the Optimised Guess Transition State
Item Value Threshold Converged?
Maximum Force 0.000065 0.000450 YES
RMS Force 0.000011 0.000300 YES
Maximum Displacement 0.001220 0.001800 YES
RMS Displacement 0.000255 0.001200 YES
Predicted change in Energy=-3.042200D-08
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. Also the RMS gradient is very small, which confirms that the optimization calculation is successful.
The optimization ends to give a structure as above, which has an imaginary frequency of magnitude -955.70 cm-1, which corresponds to the Diels-Alder reaction. The animation for the it shows a synchronous reaction pathway since two sigma bonds are developing between the two terminal carbons on butadiene and the two carbon atoms on ethene at the same time. However, the lowest positive frequency appears to show the separate motions of two fragments. This could not be regarded as a bond forming process for Diels-Alder reaction. Two fragments are not interacting with each other, and this process could be regarded as independent vibrations of reactants. Both the animations are shown below,
| Imaginary Frequency | The Lowest Positive Frequency |
|---|---|
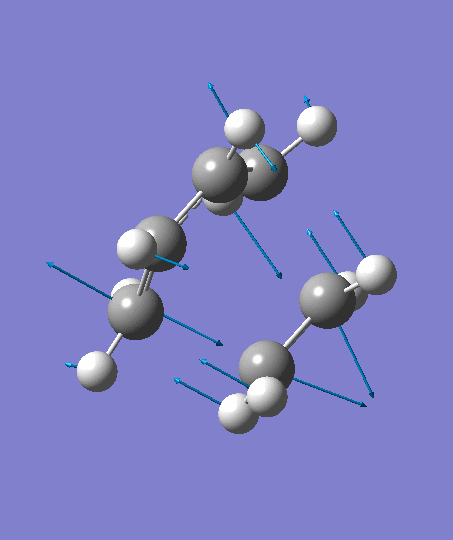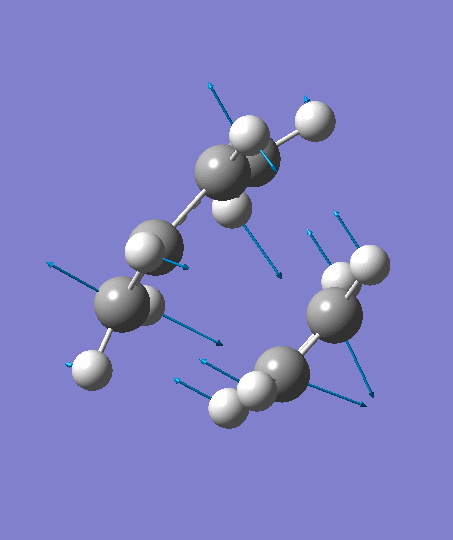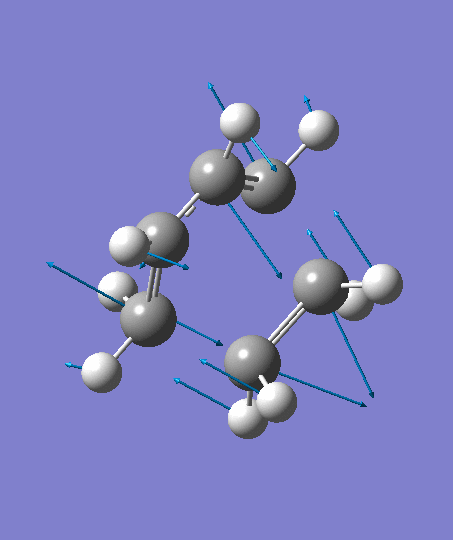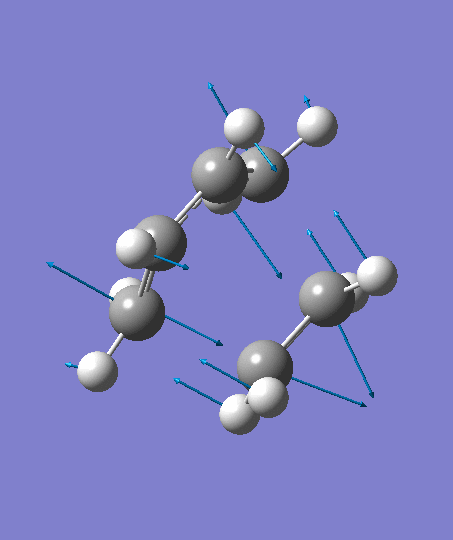 |
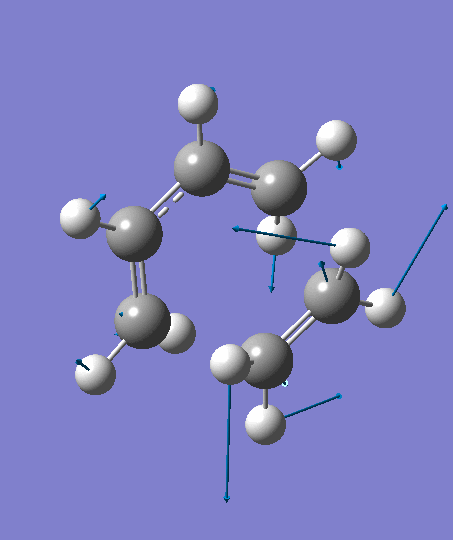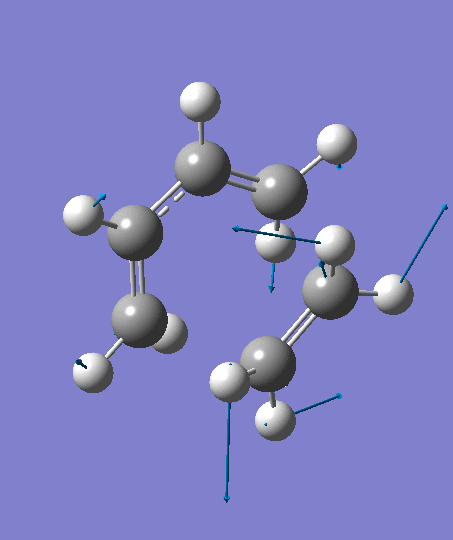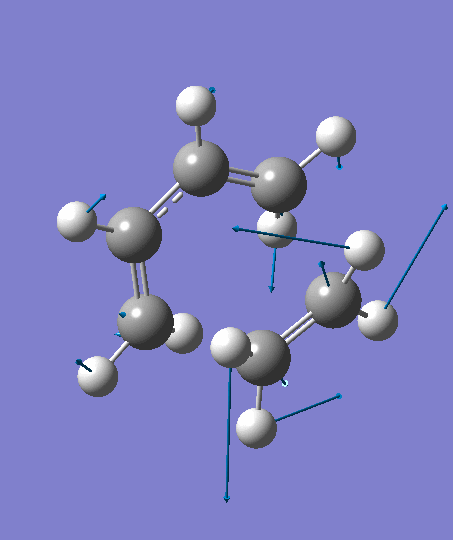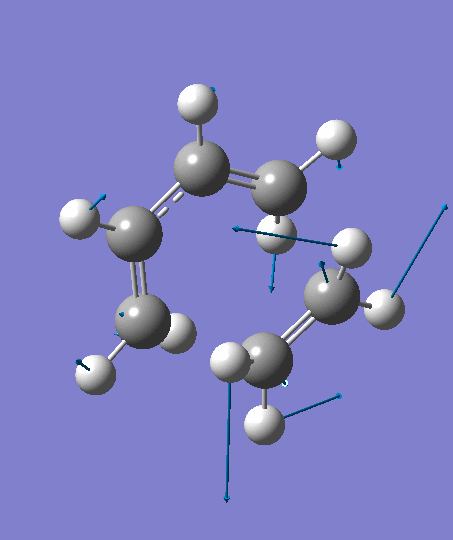
|
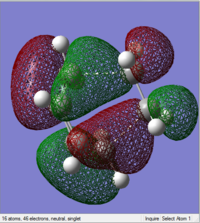
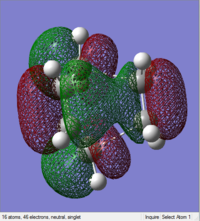
| HOMO | LUMO |
|---|---|
 |
|
The HOMO (17) is antisymmetric to the plane between the central carbon atoms on the butadiene molecule, and this corresponds to a nodal plane. The LUMO (18) is symmetric with respect to the plane between the central carbons on the butadiene molecule.
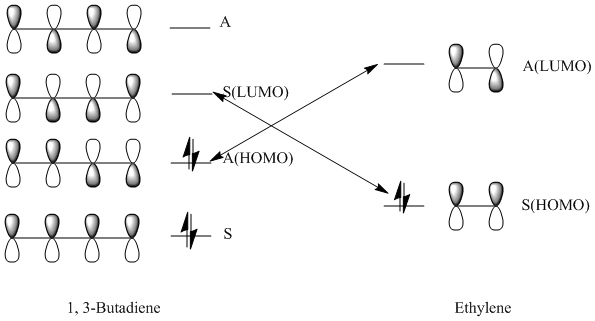
1, 3-butadiene is regarded as a substituted alkene due to the presence of the conjugated pi system. The terminal carbon atoms have the largest concentration of electron density, which correspond to the reactive sites. There are four pi orbitals and four pi electrons in butadiene and the molecular orbitals are shown above. The lowest energy orbital does not have any nodes, the HOMO has one, the LUMO has two and there are three nodes in the highest energy orbital. The HOMO contains two electrons that could be donated, and the LUMO is unfilled, willing to accept electrons. The HOMO of 1, 3-butadiene has the same symmetry as the LUMO of ethene, thus the reaction takes place via donation of electrons from the HOMO of the 1, 3-butadiene to the LUMO of the alkene. Moreover, two new sigma bonds and a new pi bond are formed via a six-centred transition state in this symmetry allowed reaction.
File Link
The optimisation file is liked to here
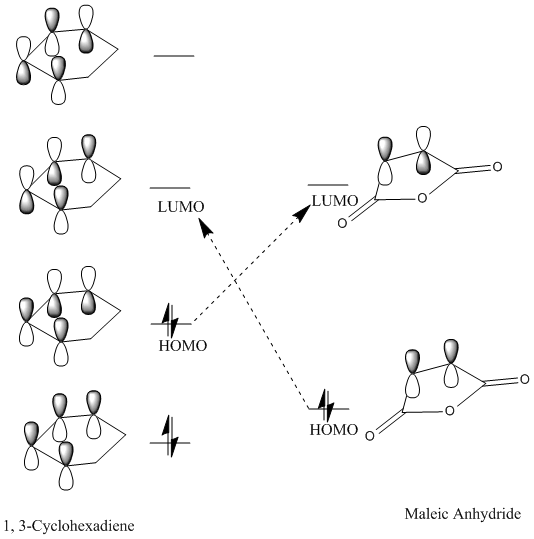
Diels-Alder Reaction between Maleic Anhydride and 1,3-Cyclohexadiene
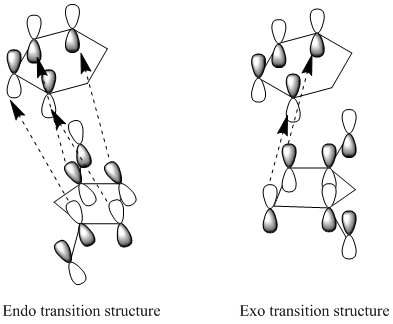
In this part, we are considering the Diels-Alder reaction between maleic anhydride and 1, 3-cyclohexadiene. Maleic anhydride is electron deficient as there are two electron-withdrawing carbonyl groups on it. The conjugation with carbonyl groups would lower the energy of the pi* orbital of the alkene, which ensure regioselective Diels-Alder reactions. There are two possible products-the exo product and the endo product. The endo product is the kinetic product, whereas the exo product is the thermodynamic product. Since the reaction is under kinetic control, the endo product would be the major product due to the lower energy of the endo transition state. This is due to the bonding interaction between the developing pi bonds at the back of the diene and the carbonyl group.
However, if the reaction is reversible and the thermodynamic exo product would be the major product. For it, there are two bridges across the ends of the two developing sigma bonds between the two reagents. Less steric hindrance is experienced when the one-C-atom bridge eclipses the anhydride ring.
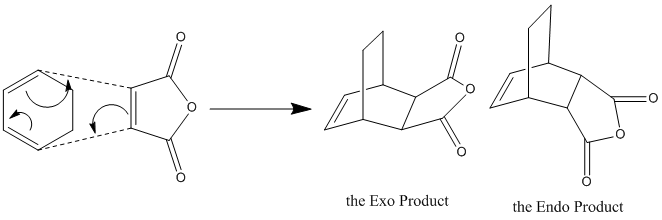
To examine the more stable transition structure, we need to do an optimisation on the guessing transition structures. For this aiming, we need to build up the guess structures as below.
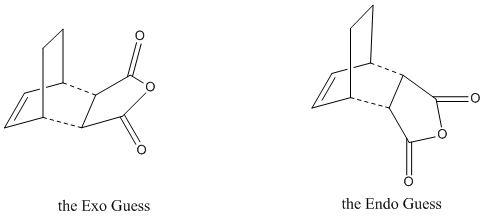
Optimisation of the Exo Product
The molecule is optimized using the semi-empirical AM1 level of theory with frequencies calculated, choosing optimization to a TS(Benny), calculating the force constants once and additional words Opt=No Eigen. The word NoEigen allows to preventing the calculation from clashing when more than one imaginary frequency is found during the process.
Optimised Exo Product
test molecule |
General Information
| Point Group | Cs |
| Energy | -0.05041983 a.u. |
Real Output of Optimised Exo Product
Item Value Threshold Converged?
Maximum Force 0.000021 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.001269 0.001800 YES
RMS Displacement 0.000317 0.001200 YES
Predicted change in Energy=-2.049253D-08
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
The optimization ends to give a structure as above, which has an imaginary frequency of magnitude -812.19 cm-1, which corresponds to the Diels-Alder reaction. The animation for the it shows a synchronous reaction pathway . However, the lowest positive frequency of magnitude 60.85 cm-1 appears to show the separate motions of two fragments. This could not be regarded as a bond forming process for Diels-Alder reaction. Both the animations are shown below,
| Imaginary Frequency | The Lowest Positive Frequency |
|---|---|
 |
|
| HOMO | LUMO |
|---|---|
 |
|
 |

|
File Link
The optimisation file is liked to here
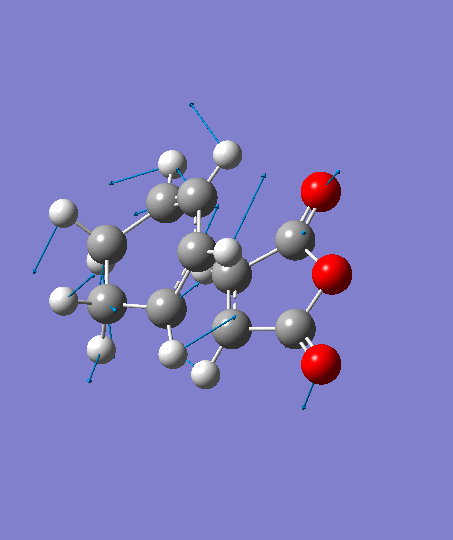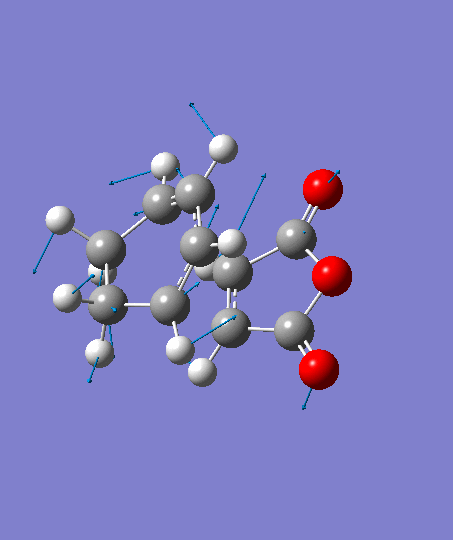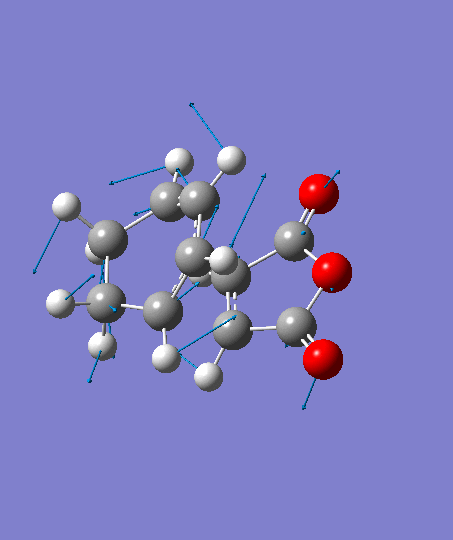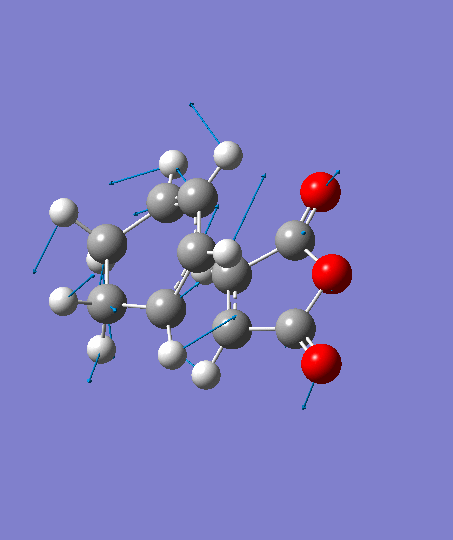
Optimisation of the Endo Product
The molecule is optimized using the semi-empirical AM1 level of theory with frequencies calculated, choosing optimization to a TS(Benny), calculating the force constants once and additional words Opt=No Eigen. The word NoEigen allows to preventing the calculation from clashing when more than one imaginary frequency is found during the process.
Optimised Endo Product
test molecule |
General Information
| Point Group | Cs |
| Energy | -0.05150476 a.u. |
Real Output of Optimised Endo Product
Item Value Threshold Converged?
Maximum Force 0.000074 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.001526 0.001800 YES
RMS Displacement 0.000302 0.001200 YES
Predicted change in Energy=-4.659817D-08
Optimization completed.
-- Stationary point found.
From the data, the force and displacement are shown to be converged, which confirms the stationary point with energy minima. And this confirms that the optimization calculation is successful.
The optimization ends to give a structure as above, which has an imaginary frequency of magnitude -806.26 cm-1, which corresponds to the Diels-Alder reaction. The animation for the it shows a synchronous reaction pathway . However, the lowest positive frequency of magnitude 62.42 cm-1 appears to show the separate motions of two fragments. This could not be regarded as a bond forming process for Diels-Alder reaction. Both the animations are shown below,
| Imaginary Frequency | The Lowest Positive Frequency |
|---|---|
 |
|
| HOMO | LUMO |
|---|---|
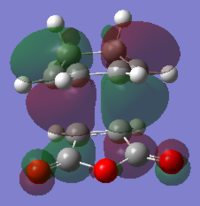 |

|
 |
|
File Link
The optimisation file is liked to here
Disscussion
Bond Length Comparison
| Diene C=C | Diene developing C=C | Dienophile C=C | |
|---|---|---|---|
| Endo | 1.39 Å | 1.40 Å | 1.41 Å |
| Exo | 1.39 Å | 1.40 Å | 1.41 Å |
The bond lengths are the same for both endo and exo transition structure, this confirms that the Diels-Alder reaction takes place via a cyclic transition state in a concerted manner.
For the geometry considerations, more preferred transition state should be less strained and should have more secondary orbital interacitons between the pi orbitals of the -(C=O)-O-(C=O)- system and the carbon-carbon double bonds. The exo form is more strained because carbons in the carbon bridges eclipses the anhydride ring, whereas this strain is not in presence in the endo transition structure.
Energy Comparison
| Exo Transition State | Endo Transition State |
|---|---|
| -0.05041983 a.u. | -0.05150476 a.u. |
ΔE=(-0.05041983)-(-0.05150476)
= 0.00108493 a.u.
= 0.681 kcal/mol
MO considerations
For the interaction between the HOMO of 1, 3-cyclohexadiene and the LUMO of maleic anhydride, the symmetry is right. When the arrangement is changed to the opposite, then the symmetry for the interaction between the LUMO of 1, 3-cyclohexadiene and the LUMO of anhydride is also correct.
From the obtained MO diagram, we can conclude that the HOMO of the transition structure is resulted from the interaction between the LUMO of the maleic anhydride and the HOMO of the 1, 3-cyclohexadiene. This is due to the lowering of energy for the LUMO of maleic anhydride in the presence of electron-withdrawing carbonyl groups.
The dienes would react with the electrophiles quickly as they have a relatively higher energy HOMO. For alkenes, their LUMOs are relatively higher in energy and the large energy gap would make the overlap poorer. However in this case, the double bond is conjugated with an electron-withdrawing group carbonyl, which lowers the energy of the alkene LUMO. Then the energy mismatch becomes quite small and would result in larger stabilisation energy according to the Klopman-Salem Equation.
As obtained from the calculation, the energies of the exo transition structure and the endo transition structure are very close. But the endo is slightly lower in energy, which confirms the endo transition state is more stable.
As shown in the calculate MO above, the HOMOs and LUMOs for both the endo transition state and the exo transition state are both antisymmetric with respect to the plane between the central carbon atoms on the hexadiene molecule. And this nodal plane bisects the -(C=O)-O-(C=O)- fragment of the maleic anhydride.
Secondary orbital overlap is defined as the positive overlap of nonactive components in the frontier molecular orbitals of a pericyclic reaction. The carbon atoms involved in the secondary orbital are not included in any bond formation process.
In the HOMO of the endo transition structure, the secondary orbital overlap is present since the p orbitals on the carbonyl carbons(on the -(C=O)-O-(C=O)-fragment) have the same phases as the central carbon atoms on the hexadiene molecule. This leads to a bonding interaction between the carbonyl groups of the maleic anhydride and the developing pi bond on the hexadiene molecule. Moreover, this overall stabilises the strucutrue.
In the HOMO of the exo structure, the two molecules are oriented away from each other. Although the p orbitals on the carbonyl carbons phaes the same as the central carbon atoms on the hexadiene molecule(on the -(C=O)-O-(C=O)-fragment), they are not close enough to interact. Thus this stabilising effect is absent for the exo transition state.
Therefore, the preferred structure should be endo structure and this confirms the endo structure is lower in energy.
Further Discussion
In this experiment, we have not take the solvent effect into considerations. By changing different solvents, the favoured transition structure may alter to the exo transition structure.
References
- ↑ F.H. Allen, O. Kennard, D.G. Watson, L. Brammer, A. G. Opren, R. Taylor, Tables of Bond Lengths determined by X-Ray and Neutron Diffraction. Part 1. Bond Lengths in Organic Compounds., J. Chem. Soc. Perkin Trans. 2., 1987, S6-S7., DOI:http://pubs.rsc.org/en/content/articlepdf/1987/p2/p298700000s1
- ↑ J. Clayden, N. Greeves, S. Warren, P. Wothers Organic Chemistry., OUP 2001, PP905-920.,
- ↑ JM. A. Fox, R. Cardona, N. J. Kiwiet, Steric effects vs. secondary orbital overlap in Diels-Alder reactions. MNDO and AM1 studies, J. Org. Chem., 1987, 52(8), pp 1469-1474 DOI: 10.1021/jo00384a016