Rep:MOD:Jr814

Introduction

File:Potential Energy Surface and Corresponding Reaction Coordinate Diagram.png

Figure 1 Potential energy surface and Corresponding Reaction Coordinate Diagram

As the potential surface shown in figure 1, there are various pathways for a reaction to take place from reactants A towards product C. A transition state that a reaction is most likely to pass is the one with lowest energy compared to other states perpendicular to the reaction path. Meanwhile, transition state is also the highest energy state in one reaction pathway. The frequency of the vibrational mode at transition state is an imaginary number hence computationally showed as a negative value. The curvature which is the secondary derivative at transition state should be negative based on the definition of the transition state being the local maximum. Therefore the frequency is an imaginary number due to the fact that the square root of -1 is i.

The minimum on the potential energy surface can be referred to either global minimum or local minimum. A global minimum is the minimum energy point when looking at all possible reaction pathways ,which generally can be regarded as the most thermodynamically stable structure. A local minimum is the the minimum energy point in a certain range of reaction coordinates, such as reactants or products. All minima should have positive frequency and positive curvature.

The gradient at both minimum and transition state should be zero because both of them are at stationary points.

Nf710 (talk) 00:42, 18 November 2016 (UTC) Very good. SO the PES has 3N-6 dimensions. AT a TS they are all postive curvature apart from one which is the minimum ebergy path way and hence the imaginary frequency.

Exercise 1

Figure 2 Reaction of Butadiene with Ethylene

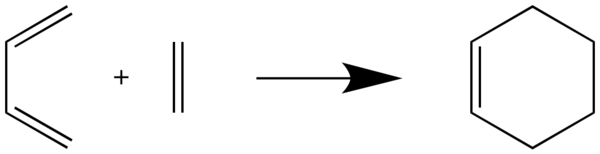
In this exercise, the Diels-Aleder reaction of butadiene and ethylene is investigated by considering the orbital interactions as well as the bond distance variation during the course of reaction

Frontier molecular orbital description of Diels-Alder Reaction between butadiene and ethene

Compound	MO1	MO2	MO3	MO4
Transition state

Compound	HOMO	LUMO
Butadiene	The HOMO of butadiene calculated with PM6	The LUMO of butadiene calculated with PM6
Ethene	The HOMO of ethene calculated with PM6	The LUMO of ethene calculated with PM6

Figure 4 Frontier_orbital_description of cycloaddition

Figure 3 MO diagram of Diels-Alder reaction between butadiene and ethene

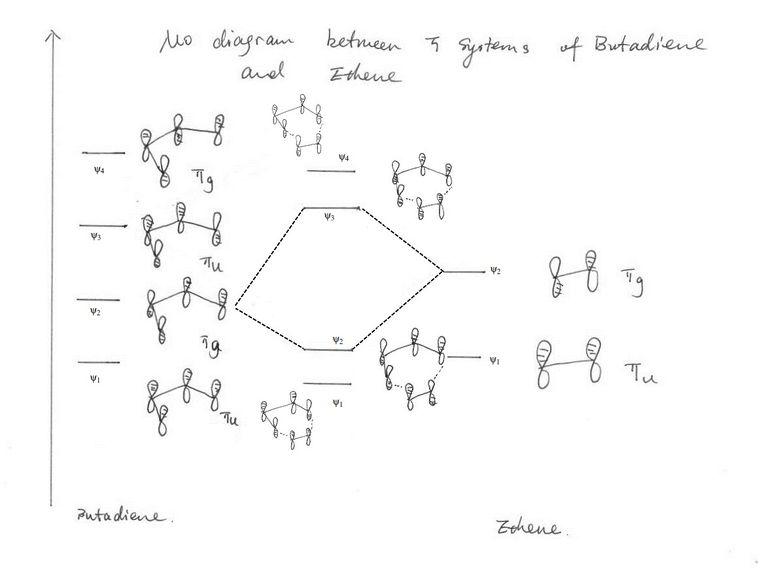
By comparing the MO diagram drawn on figure 3 and the HOMO and LUMO for butadiene, ethene and the transition state, it is clear that MO1 and MO3 for transition state are made up from the HOMO of butadiene and the LUMO of ethene, MO2 and MO4 are formed by combining the LUMO of butadiene and the HOMO of ethene. This is not what we generally expect for a normal demand Diels-Alder reaction which is the case for butadiene and ethene reaction. As suggest in figure 4 , the energy gap between two π_g orbitals are too large to interact, hence the interaction is dominated by the HOMO of butadiene and the LUMO of ethene. For a reaction to proceed, two orbitals overlapping require the same symmetry, i.e. gerade reacts with gerade, and close in energy. For a bond to form, positive phase of the orbital can only overlap with the positive phase of the other orbital. Therefore, the overlapping integral <ψ₁|ψ₂> is equal to zero for gerade-ungerade interaction but non-zero for gerade-gerade and ungerade-ungerade interactions.

Analysis of C-C bond distances

The bond distances are extracted using Python,and the results are plot as below.

Figure 5 Internuclear distance within reactants during the reaction

Figure 6 Internuclear distances of newly formed C-C during the reaction

C-C bond distances in reactants and products

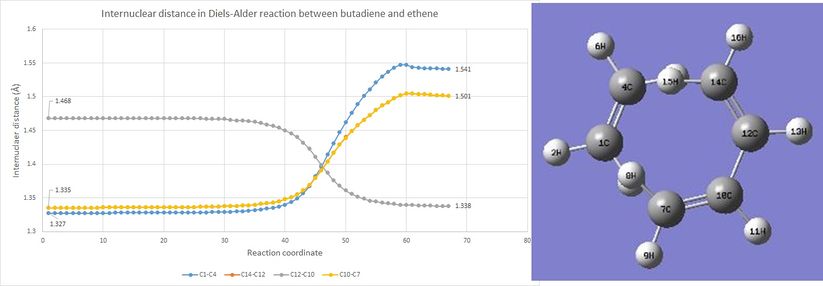
Bond distance(Å)	C1-C4	C14-C12	C12-C10	C10-C7	C4-C14	C1-C7
Butadiene		1.3353	1.4684	1.3353
Ethene	1.3273
Product	1.541	1.550	1.338	1.550	1.54003	1.54004

Typical C-C bond distances

	sp3 C-sp3 C	sp2 C-sp2 C
Bond distance(Å)	1.54	1.47

During the reaction,the bond distances of all three original double bonds (C1-C4, C7-C10 and C14-C12) increase as they progress to C-C single bonds. As shown in figure 5, the curves for C7-C10 and C14-C12 ouverlap to each other as they are equivalent in this symmetrical butadiene. In the meantime, C12-C10 becomes shorter in distance as it becomes a C-C double bond and ends at 1.338 Å, which is shorter compared to a typical sp² C-sp² C bond distance.

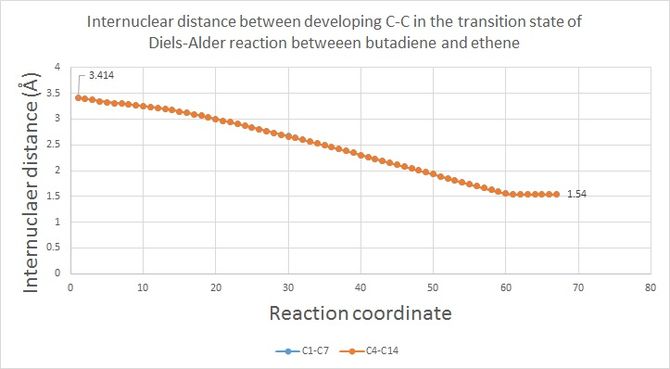
According to figure 6,the two newly formed C-C single bonds have bond distances starting from 3.413 Å, which is about twice of the Van der waals radius for C (1.7 Å ), and end up at 1.54 Å that is exactly the same compared to typical sp³ C-sp³ C bond distance. The bond length of partly formed C-C bond during the transition state falls in between these two values.

Vibration of transition state

Figure 7 the vibration of transition state with -948.99cm^-1

Figure 8 the vibration with the least positive frequency

At transition state, the vibration is as shown in figure 7, in which the frequency of the vibration is -948.99 cm^-1. The frequency of transition state is an imaginary number but represented as a negative value. It is imaginary number due to a simple mathematical result from square root of -1 when solving equations for force constant that is a negative value.

The vibration with the lowest positive frequency at 145.18 cm^-1 is shown in figure 8. Comparing with the transition state vibration, these vibrations are purely independent of each other, which can be described as the energy exchange only happens within one normal mode and never exchanges to another. The one with negative frequency describes the formation of two bonds synchronously (hence Diels-Alder reactions are concerted reactions).

Nf710 (talk) 00:49, 18 November 2016 (UTC) This exercise was done really well, good understand and your analysis of the MOs was excellent.

Exercise 2

Figure 9 [4+2]-cycloaddition between benzoquinone and cyclopentadiene

In this exercise, the [4+2]-cycloaddition between benzoquinone and cyclopentadiene is investigated in terms of thermodynamic and kinetic control of the two possible products.

Frontier Oribital Analysis of Diels-Alder reaction between Benzoquinone and Cyclopentadiene

Molecular orbitals of the transition state invovled in the formation for both endo and exo products

Transition state	HOMO	LUMO
ENDO	The HOMO of endo T.S. calculated with B3LYP/6-31G(d)	The LUMO of endo T.S. calculated with B3LYP/6-31G(d)
EXO	The HOMO of exo T.S. calculated with B3LYP/6-31G(d)	The LUMO of exo T.S. calculated with B3LYP/6-31G(d)

As shown in the table on the left, the HOMO of both transition states have π_g symmetry while the LUMO of both transition states have π_g symmetry as well because in both cases, these orbitals are resulted from the overlapping between the HOMO of cyclopentadiene and the LUMO of benzoquinone, both of which contains π_g symmetry. This is what as expected from a normal demand Diels-Alder reaction.

(These aren't the converged structures that you're displaying with Jmol. You need to find the most optimised model and select it with "frame <MODEL>" Tam10 (talk) 15:25, 9 November 2016 (UTC))

Calculating reaction barrier and reaction energy

Sum of electronic and thermal free energies of reactants, two transition states and two products

	Benzoquinone	Cyclopentadiene	Endo transition state	Exo transition state	Endo product	Exo product
sum of electronic and thermal free energies (Hartree/Particle)	-381.396831	-194.034782	-575.383852	-575.381306	-575.427053	-575.426692

For Endo:

^ΔG^†= [-575.383852-(-381.396831-194.034782)]×627.5095×4.184= +125.40 kJ/mol

^ΔG= [-575.427053-(-381.396831-194.034782)]×627.5095×4.184= +11.97 kJ/mol

For Exo:

^ΔG^†= [-575.381306-(-381.396831-194.034782)]×627.5095×4.184= +132.08 kJ/mol

^ΔG= [-575.426692-(-381.396831-194.034782)]×627.5095×4.184= +12.92 kJ/mol

Based on the calculation above, Endo reaction has lower activation energy hence endo product is the kinetically favourable product. This can be due to the fact that during the transition state, there is a stabilizing interaction between developing π system on cyclopentadiene and one of the double bonds on benzoquinone that is below the plane of the cylcopentadiene. Generally it is expected that the exo product is the thermodynamic product. This can be explained in terms of steric hindrance by considering two bridges across the ends of the new bonds: a one-O-atom bridge and a two-C-atom bridge. There is less steric hindrance if the smaller (that is, the one-atom) bridge eclipses benzoquinone ring while the more bulky (2-C) bridge staggers the benzoquinone ring. However, based on the calculations above, it turns out that the endo product is also the thermodynamic product. This could be because the strong favourable secondary orbital interaction between the newly formed π system and the π system below on the benzoquinone ring overrides the unfavourable steric clashes by eclipsing with the larger ring. Both reaction pathways gives less thermodynamically stable products as both reactions are slightly endothermic.

Nf710 (talk) 00:59, 18 November 2016 (UTC) This part was done very well well and consisly. However you have calculated you reactants at infinite separation when it should be done as teh reactant point on the IRC and then optimized down. as thee is a separation interaction. But you have still come to the correct conclusions.

Exercise 3

Figure 10 Two possible reactions between o-xylylene and so2

In this exercise, three possible reaction pathways for o-xylylene and sulfur dioxide reaction including Diels-Alder endo, Diels-Alder exo and cheletropic reaction are investigated in terms of the transition state and product energies.

Optimization results

Table of transition state vibrations and the optimized products for all three possible reaction pathways

Reaction pathway	Transition state vibration	Adducts
Diels-Alder Endo	638×323px frequency = -333.37 cm-1
Diels-Alder Exo	638×323px frequency = -351.11 cm-1
Cheletropic	638×323px frequency = -486.70 cm-1

IRC for three possible reaction pathways

IRC for three possible reaction pathways for reactions between sulfur dioxide and o-xylylene

Reaction pathway	IRC
Diels-Alder Endo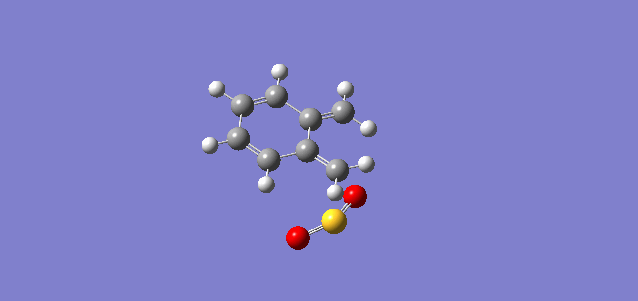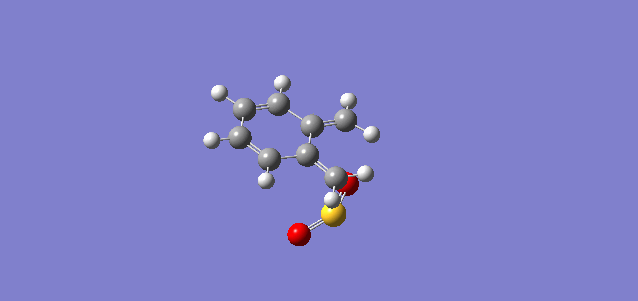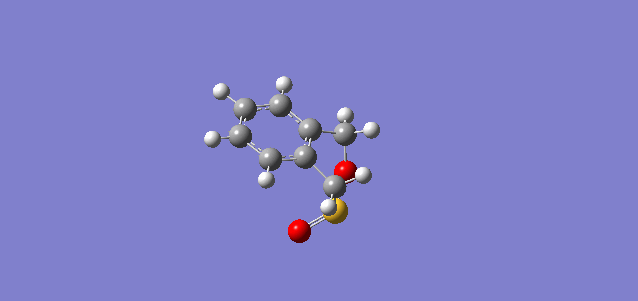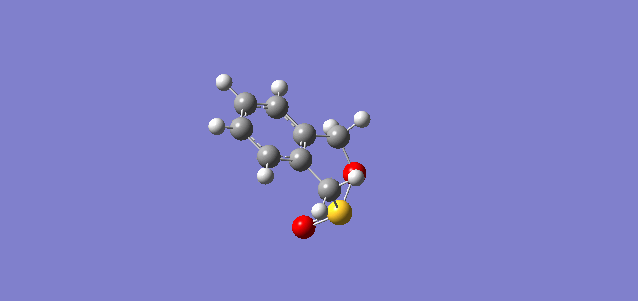
Diels-Alder Exo
Cheletropic

As shown in the table on the left, the computational IRC shows that the bond formation for cheletropic pathway is synchronous, whereas the bond formation for both endo and exo pathways are asynchronous with C-O bond forms first. This can be due to the fact that oxygen has smaller Van der Waals radius than sulfur that is one period down the oxygen.

During the formation of new sigma bonds, the 6-membered ring in the o-xylylene becomes an aromatic system with 6 delocalized π electrons.

Reaction barrier and Reaction energies calculations

Figure 11 Reaction profile for all three reaction pathways

Sum of electronic and thermal free energies of reactants, transition states and products for three reaction pathways

sum of electronic and thermal free energies (Hartree/Particle)	o-Xylene	Sulfur dioxide	Transition state	product
Diels-Alder Endo	0.178108	-0.118614	0.090560	0.021700
Diels-Alder Exo	0.178108	-0.118614	0.092076	0.027460
Cheletropic	0.178108	-0.118614	0.099061	-0.000002

For Diels-Alder Endo:

^ΔG^†= [0.090560-(0.178108-0.118614)]×627.5095×4.184= +81.56 kJ/mol

^ΔG= [0.021700-(0.178108-0.118614)]×627.5095×4.184= -99.23 kJ/mol

For Diels-Alder Exo:

^ΔG^†= [0.092076-(0.178108-0.118614)]×627.5095×4.184= +85.54 kJ/mol

^ΔG= [0.027460-(0.178108-0.118614)]×627.5095×4.184= -84.11 kJ/mol

For Cheletropic:

^ΔG^†= [0.099061-(0.178108-0.118614)]×627.5095×4.184= +103.88 kJ/mol

^ΔG= [-0.000002-(0.178108-0.118614)]×627.5095×4.184= -156.21 kJ/mol

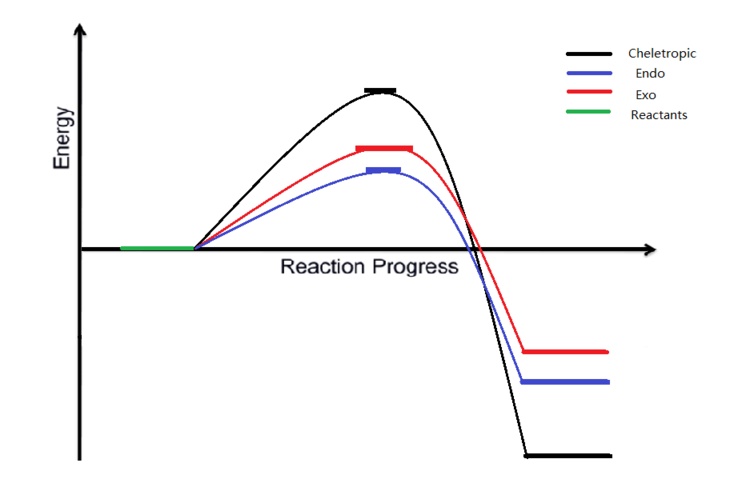
Based on the calculations and the reaction profile in figure 11 above, Diels-Alder endo pathway has the lowest activation energy with +81.56 kJ/mol, whereas cheletropic reaction pathway has the highest activation energy with +103.88 kJ/mol. It can be explained by close observation on the IRC result above. As the synchronous C-S bond formation takes place, two small oxygen atoms are pushed into close proximity and experience unfavorable electron-electron repulsion that results in high energy transition state.

Considering the thermodynamic properties of the products, it turns out that the cheletropic product is the most thermodynamically favorable product while the exo product is the least one, which is generally not expected to be less stable than endo product. The highly thermodynamic stability of cheletropic product could be possibly due to the high symmetry of the molecule.

(It's probably due to the formation of a less strained ring (considering that S is larger than C) Tam10 (talk) 15:25, 9 November 2016 (UTC))

Reaction with second cis-butadiene fragment in o-xylyene

IRC of reaction with second cis-butadiene fragment in o-xylyene

Reaction pathway	IRC
Diels-Alder Endo	938×323px
Diels-Alder Exo	938×323px

Sum of electronic and thermal free energies of reactants, transition states and products

sum of electronic and thermal free energies (Hartree/Particle)	o-Xylene	Sulfur dioxide	Transition state	product
Diels-Alder Endo	0.178108	-0.118614	0.102070	0.065610
Diels-Alder Exo	0.178108	-0.118614	0.105055	0.067304

For Diels-Alder Endo:

^ΔG^†= [0.102070-(0.178108-0.118614)]×627.5095×4.184= +111.78 kJ/mol

^ΔG= [0.065610-(0.178108-0.118614)]×627.5095×4.184= +16.06 kJ/mol

For Diels-Alder Exo:

^ΔG^†= [0.105055-(0.178108-0.118614)]×627.5095×4.184= +119.62 kJ/mol

^ΔG= [0.067304-(0.178108-0.118614)]×627.5095×4.184= +20.51 kJ/mol

According the calculations, both reaction pathways have much higher activation energies than reacting with the butadiene fragment outside the ring. Both products have higher energies than the reactants. Therefore, two reaction pathways are both thermodynamically and kinetically unfavourable.

Conclusion

After three exercises, it is clear that there are several pros and cons on using computational methods for analyzing a reaction.

For the advantages, computational methods give a convenient and informative explanation of how a reaction pathway goes (IRC). The thermodynamic data about reactants, transition states and products can be extracted and help chemists to determine possible outcomes of the reaction without physically doing the bench work. The most striking thing about using computational methods is to visualize molecular orbitals easily and give relatively accurate graphical representations to those quantum objects.

However, in the exercises above, the program did not take into account of the reaction conditions applied for those cycloadditons, which generally require heat. And the predictions made can mismatch with the experimental outcomes.For example, in reality, Butadiene rarely reacts with ethene to form cyclohexene. Butadiene is not a perfect diene as there is a possibility for it to adopt a s-trans conformation and ethene is a really poor dienophile because it has such a high energy LUMO that it can not interact with the HOMO of the diene. But as the results shown in exercise 1, the program simply picked up two MOs closest in energy and give a prediction of the reaction outcomes without considering the reaction conditions.

Also, different basis sets and calculation methods use different approximations and can lead to different results. Generally the more complex and accurate the method is, the more time-consuming the method will be (IRC in exercise 2 took me 12 hours to run).

The last but not the least, the reaction pathway that the program run is manually chosen as the program can not give all the possible reaction pathways straightaway. Therefore, it is only possible to investigate the regioselectivity ,stereoselectivy and different mechanisms of the reaction between the same reactants if we set each reaction pathway up first.