Rep:MOD:JG123
Characterisation of Cope Rearrangement and Diels Alder Cycloaddition Transition States
Cope Rearrangement

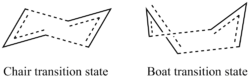
Overview
The Cope rearrangement (figure 1) is an example of a [3,3]-sigmatropic shift. This pericyclic reaction proceeds via a 6-electron aromatic transition state. This transition state has been computationally shown to proceed via two conformations, boat or chair (figure 2. These will be re-examined to determine which is of lower energy and in turn which provides a more favourable route for the reaction to occur.
Optimising 1,5-hexadiene
Although the reaction may look simple when drawn with 2 dimensional molecules, the potential energy surface (PES) has many maxima and minima that correspond to the various 3D conformers of 1,5-hexadiene. Furthermore the complexity of this surface is increased as the difference in energy between gauche and anti conformers is small, dissimilar to analogous saturated alkanes. [1] For each conformer there would be either zero, one or two local maxima (Transition states are not exactly maxima João (talk) 11:27, 24 December 2014 (UTC)): zero, indicating that the conformer can not undergo the rearrangement (Does this situation exist? Would the molecule be stuck in that configuration forever? A better description is in term of accessibility: there are many transition state structures leading to different conformers, and some have lower energy than others making them accessible at a given temperature. João (talk) 11:27, 24 December 2014 (UTC)); one, indicating the rearrangement can only proceed exclusively through boat or exclusively through chair transition states; two, indicating the conformer can rearrange via either boat or chair transition state. Therefore there is huge difficulty in mapping out the whole potential energy in surface and instead only certain minima are found and the surface surrounding them studied.
To optimise structures only two methods were used during this experiment (What follows suggest some minor misconceptions, but the important thing to note is that both Hartree-Fock and DFT are methods to calculate the electronic energy, they don't optimize structures. One uses the derivatives of this energy to optimize relevant geometries for the chemical reaction. João (talk) 11:27, 24 December 2014 (UTC)). A Hartree Fock optimisation (HF) using 3-21G and a higher level of theory, Density Functional Theory (DFT) B3LYP/6-31* optimisation using 6-31G(d) as a basis set. These group quantum calculations are referred to as Ab Intio computational methods. DFT approximated electronic structure by imposing potential on the structures' electrons [2] where as HF approximated electronic structure by linearly combining single-electron wavefunctions that described each constituent atom. [3] The level of theory differs in how electron-electron repulsions are calculated. HF optimisations determined electron-electron repulsion by computing the repulsion of an average distribution of electrons on a singular electron in the system. This omitted the stabilising effect that the instantaneous movement of individual electrons can provide and in turn produced higher energy structures. The significance of these contributions in 10-100 electron systems was demonstrated by the much lower DFT optimised energies.
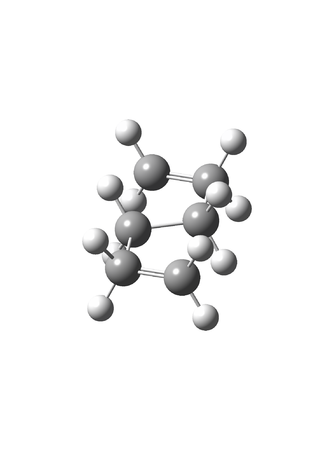
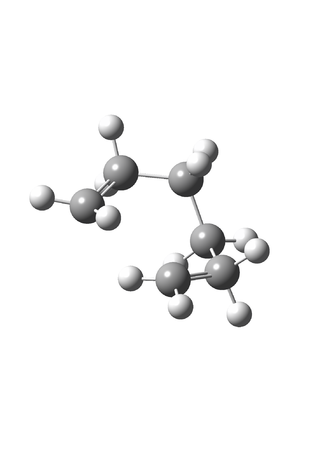
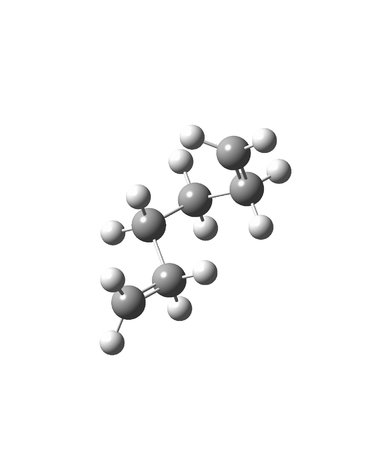
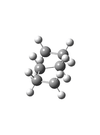
The initial attempt to find the lowest energy conformer of 1,5-hexadiene resulted in the HF computation of an anti 1 conformer with a energy of - 232.64075806 Hartrees and point group of C2h. Although most small alkenes are planar, the most stable conformation of 1,5-hexadiene would not be predicted to be planar. The HF computation of the gauche 1 structure resulted in a non-planar structure with a higher energy of - 232.63838256 Hartrees and point group of C2, indicating that the planar conformer was more stable. These similarity in these conformer indicate an energy barrier of only 6.24 kJ mol-1 (Is this an energy barrier or energy difference between conformers? João (talk) 11:27, 24 December 2014 (UTC)).
Comparison of the first two conformers' energy led to the simple hypothesis that the anti conformers of 1,5-hexadiene are lower in energy than gauche conformers;the HF computation of the anti 2 structure with an energy of - 232.63015166 Hartrees led to this hypothesis being disregarded. HF optimisation of the lowest energy conformer, gauche 2, resulted in a total energy of - 232.88067699 Hartrees and a point group of Ci.
Subsequent higher theory DFT optimisations lead to the energies of the conformer molecules decreasing significantly. In spite of the similarity of their HF optimised energies, the conformers retained their relative order of energy (And how do the geometries compare? João (talk) 11:27, 24 December 2014 (UTC)). All these conformers are demonstrated in figure 3 and their respective energy data observed in Table 1. To prove that the gauche 2 conformer found was a minima on the PES, a frequency calculation was run to find all vibrations of the molecule. Results indicated only positive real vibrational frequencies; any non-real frequencies would indicate that the structure was a transition state and therefore a maxima on the PES.
N.B. Names of conformers were assigned systematically.
-
Anti 1 optimised conformer
-
Gauche 1 optimised conformer
-
Anti 2 optimised conformer
-
Gauche 2 optimised conformer
The following thermodynaic properties were found for the gauche 2 conformer: Sum of electronic and zero-point energies = -235.680589 Hartrees Sum of electronic and thermal energies = -235.672979 Hartrees Sum of electronic and thermal enthalpies = -235.672035 Hartrees Sum of electronic and thermal free energies = -235.712244 Hartrees
Optimising Chair and Boat Transition States
To optimise the transition states, three techiques were used:
- Berny optimisation: optimises a guess of the transition state.
- Fixed coordinate optimisation: finds the transition state by first fixing the coordinates of the bond forming atoms, optimising that structure and subsequently optimising the distance between those atoms.
- QST2 optimisation: optimises a transition state by comparing reagents and products with labels for the corresponding atoms.
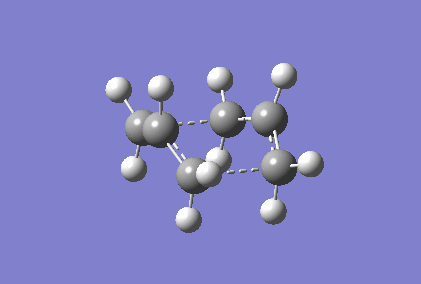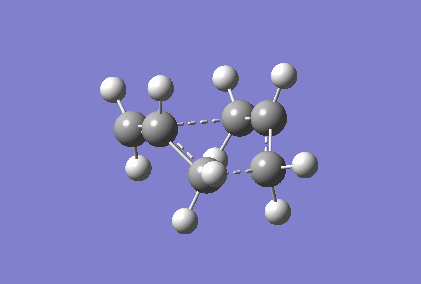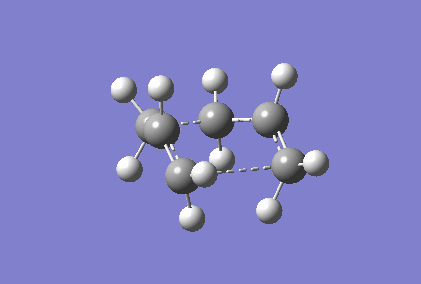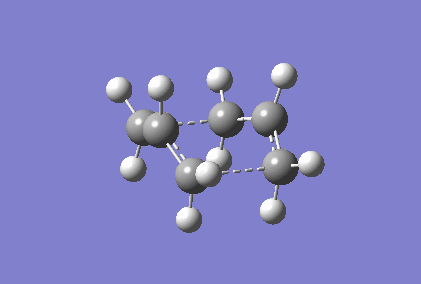
Berny optimisation of chair transition state: An HF optimised allyl group was duplicated. The two allyl groups were approximately aligned in the chair transition state. A Berny transition state frequency and optimization calculation of this structure elucidated an imaginary frequency of - 568.24 cm-1 which corresponding to the Cope rearrangement as demonstrated by the animation in figure 4. A singular imaginary frequency indicated that this structure was the transition state.
The distance between the terminal carbon atoms of the allyl groups is 1.98587 Å and 1.98597 Å. These similar distances correspond to the breaking and formation of the C-C sigma bonds, which have an average bond length of 1.54 Å[4]. Comparison of the terminal distances to this average bond length would suggest there is no bonding character however, the mean Van der Waals radius for carbon is 1.70 Å[5]; there would be substantial orbital overlap at a C-C of 1.986 Å. Total energy of this transition state was - 234.57201473 Hartrees. To determine what conformer the product of this transition state was a forward intrinsic reaction coordinate calculation, to find a local minima, was attempted. The computation proved to be unsuccessful. Repeat failure of the calculation with reoptimised chair transition states led to the diagnosis that there were insufficient point calculated. (What conformer did you find at the end of your IRC computation?/span> João (talk) 11:27, 24 December 2014 (UTC))
Frozen coordinate optimisation of chair transition state: To validate this structure the a frozen coordinate method was used. With the two pairs of terminal allyl carbons frozen as if hypothetically bonded at a distance of 2.2000 Å, the overall structure was DFT optimised. Following this an attempt was made to optimise the previously fixed bond lengths. This similarly proved to be unsuccessful (What was the problem exactly? Did you check the log file? João (talk) 11:27, 24 December 2014 (UTC)) and was thought to be a result of the guess structure been too far from the chair structure.
QST2 optimisation: An initial attempt using the anti 2 conformer for a product and reagent kept failing the calculation. This is occurred as they were too far from the boat transition structure. Repetition of this process using a product and reagent form that was closer to that of the boat transition state resulted in the boat transition state being found. Dissimilar to the chair transition state, the distance between the terminal carbon atoms of the allyl groups was 2.22303 Å and 2.22251 Å. Although terminal distances we're different, the boat transition structure had a similar imaginary frequency of - 521.88 cm-1 that also animated to give the Cope Rearrangement (figure 5). The total energy of this transition state was - 234.55863984 Hartrees, indicating that the lower energy chair transition state is favored.
(Did you compute the activation energy for the reaction? How does it compare with experimental/other literature values? Did you reoptimized the transition state at higher level of theory? How would the energies and geommetries look like at this higher level of theory? João (talk) 11:27, 24 December 2014 (UTC))
Diels Alder Cycloadditions
Cycloaddition of Cis-butadiene and Ethlyene
HOMO and LUMO of Cis-butadiene
-
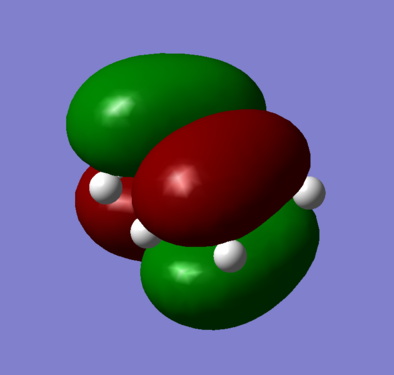
Figure 6a - Anti-symmetric HOMO of optimised butadiene
-
Figure 6b - Anti-symmetric HOMO of optimised butadiene
-
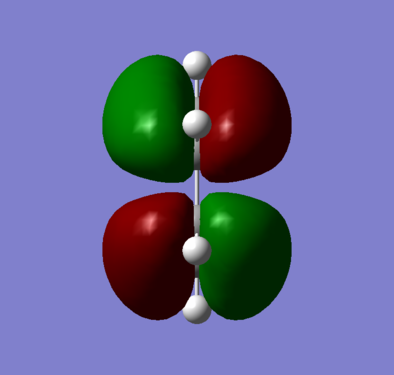
Figure 7a - Symmetric LUMO of optimised butadiene
-
Figure 7b - Symmetric LUMO of optimised butadiene
The optimised cis-butadiene was found to be planar and overall had two planes of symmetry, a σh and σv. As both the HUMO and LUMO are a combination of the p-orbitals on the cis-butadiene, both MOs were anti-symmetric with respect to the σv plane. With respect to the σh plane, the HOMO (figure 6) was found to be anti-symmetric whereas the LUMO (figure 7) symmetric.
Transition State of Cis-butadiene and Ethlyene Cycloaddition
To find the transition state a QST2 optimisation was performed. The transition state structure was found to have an envelope like geometry and an imaginary stretching frequency at - 529.24 cm-1 that corresponded to the Diels Alder reaction (figure 8). The motion of the singular imaginary frequency showed the expected bonds forming and indicated that the transition structure had indeed been found.
The partially formed sigma bond lengths in the transition state were 2.26717 and 2.26777. Typical sp3 C-C and sp2 C-C bond lengths are 1.54 Å and 1.34 Å respectively. Similar to the Cope rearrangement the large bond lengths would suggest no bonding character. However, the mean Van der Waals radius of carbon (1.70 Å) indicates there is and overlap of 1.13283 Å suggesting there is a strong bond forming attraction occuring.
Determine the synchronicity of the the bond formation seems trivial when examining figure 8. Furthermore, the identical (to 4 s.f.) partially formed sigma bond lengths support the synchronous bond formation. The lowest positive frequency vibration of 135.42 cm-1 shows a asymmetric waggling of the ethylene group. This provides conflicting evidence and suggest that asynchronous bond formation may be possible were the reaction conditions different. (There is no conflict, as the frequency is non-imaginary such motion is not part of the reaction coordinate João (talk) 11:27, 24 December 2014 (UTC))
| Energy/Hartrees | Literature Energy/Hartrees | |
|---|---|---|
| Cis-butadiene | - 155.98595131 | - 155.99214 |
| Ethylene | - 78.58745868 | - 78.58746 |
| Total for reactants | - 234.57340999 | - 234.57960 |
| Transition structure | - 234.55971792 | - 234.54389 |
| Cyclohexene | - 234.64829704 | - 234.64829 |
Activation energy of the reaction is found to be 8.59 kcal mol-1, showing poor correlation to a literature energy of 29.7 kcal mol-1 [7] These difference arise from the poorly optimised cis-butadiene structures and a more stable transition structure found.
The cycloaddition between the electron rich cis-butadiene and relatively electron poor ethylene occurs with normalelectron demand. The computed thermal π 4s + π 2s pericyclic reaction proceeds via a suprafacial Hückel topology. The pericyclic reaction rules do not forbid this reaction as overall orbital symmetry is maintained. During the reaction the HOMO of the diene interacts with the similar energy LUMO of the ethylene, which is off the same symmetry, to form the transition state orbitals Consequently, the HOMO and LUMO of the transition state were both symmetric (Why would that be the case? Did you look at the transition state orbitals or are you making a conjecture? João (talk) 11:27, 24 December 2014 (UTC)) and the symmetry of the cyclohexene product inverted (HOMO symmetric, LUMO anti-symmetric) with respect to the ci-butadiene. The high degree of symmetry in both reactants and products means that there is little stereo-control within this reaction. However the effects of secondary orbital overlap can be significant for stereoselective control, as was demonstrated by the cycloaddition of maleic anhydride and cyclohexa-1,5-diene.
Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride
Optimising Reagents and Products
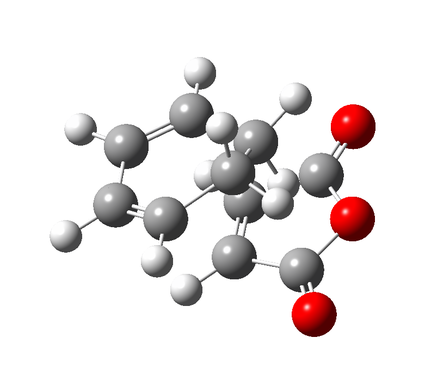
The Diels Alder reaction between cyclohexadiene and maleic anhydride allowed us to probe stereochemical control computationally. The formation of exo and endo diastereoisomers for reactions between maleic anhydride and cyclic dienes are well documented. The cycloaddition benefits from the fixed cis orientation of the diene in the cyclic ring.
DFT optimisations of the reagents, cyclohexadiene and maleic anhydride, led to two planar molecules being found with energies of - 233.41891180 Hartrees and - 379.928953542 Hartrees respectively. Similar optimisation for the endo and exo products resulted in energies of - 612.75830991 and - 612.75577825 Hartrees being found.
Finding Endo and Exo Transition states
| Energy/Hartrees | |
|---|---|
| Cyclohexa-1,3-diene | - 233.41891180 |
| Maleic anhydride | - 379.28953542 |
| Total for reagents | - 612.70844722 |
| Exo Transition structure | - 612.69441549 |
| Endo Transition structure | - 612.69836160 |
| Exo product | - 612.75577825 |
| Endo product | - 612.75830991 |
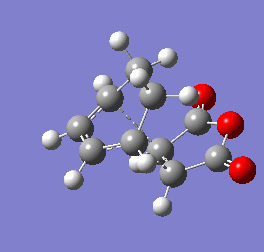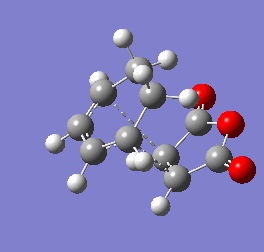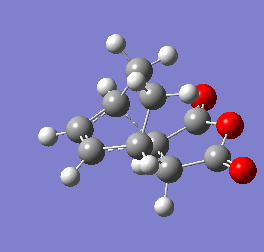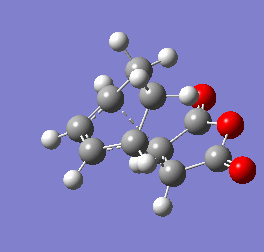
To find both transitions states the QST2 method was used. Both exo and endo transition states were found and validated through the observation of a singular imaginary frequency for each (- 450.95 cm-1 for exo,- 449.71 cm-1 for endo) that corresponded to the Diels Alder reaction. These computations are characterised in figures 9 & 10.
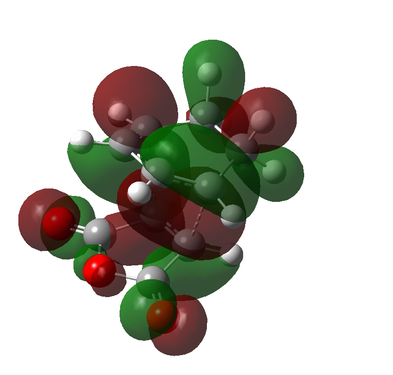
Analysis of the energies of the reagents, transitions states and products lead to conclusion that the endo product is both the kinetic and thermodynamic product as the energies of the transition state and product are lower than the analogous exo structures.The interpretation of the difference in energies comes from orbital interactions rather than discussion of bond length. The secondary orbital overlap have a significant role in the stability of the transition states. Although steric repulsion is higher in the endo transition state (Why is that so? João (talk) 11:27, 24 December 2014 (UTC)), greater favourable delocalised secondary orbital overlap (Where do you see this? João (talk) 11:27, 24 December 2014 (UTC)) outweigh this leading to the Exo transition state and product being more stable than the analogous Exo product. [9].
-
Figure 9a - Intial alignment of the reagents for the QST2 optimisation
-
Figure 9b - Imaginary stretching frequency of the transition state demonstrating to the Diels Alder reaction
-
Figure 9c - HOMO of the Exo transition state
-
Figure 9d - The optimised Exo product
-
Figure 10a - Intial alignment of the reagents for the QST2 optimisation
-
Figure 10b - Imaginary stretching frequency of the transition state demonstrating to the Diels Alder reaction
-
Figure 10c - HOMO of the Endo transition state
-
Figure 10d - The optimised Endo product
Overall, 3 pericyclic reactions we're examined successfully and the selectivity of Diels Alder reactions analysed.
References
- ↑ http://pubs.acs.org/doi/pdf/10.1021/ja00111a016
- ↑ http://link.springer.com/article/10.1007%2Fs00466-012-0728-4
- ↑ http://onlinelibrary.wiley.com/doi/10.1002/anie.199206821/pdf
- ↑ http://pubs.acs.org/doi/pdf/10.1021/cr60211a005
- ↑ http://pubs.acs.org/doi/pdf/10.1021/j100785a001
- ↑ http://pubs.acs.org/doi/abs/10.1021/ja9601494
- ↑ http://pubs.acs.org/doi/pdf/10.1021/ja00101a078
- ↑ http://pubs.acs.org/doi/abs/10.1021/ja9601494
- ↑ http://www.scielo.br/scielo.php?pid=S0103-50532010000100017&script=sci_arttext