Rep:MOD:JDN15Y3lab
Introduction
Potential Energy Surface and Transition State
The Potential Energy Surface (PES) provides a graphical relationship between the energy of a molecule and its possible structures. The PES has 3N - 6 degree of freedom, where the minima refers to the chemically stable species (i.e. reactant and product) while the saddle point refers to the transition state. A transition state is the maximum point on the minimum energy path on a PES. By taking the second derivative at these points, we can differentiate between the reactants, products and transition state as the reactants and products will have a positive curvature in all coordinates while the transition state will have a negative curvature in only 1 coordinate. By utilising Gaussian software, a transition state can also be identified by having one imaginary (negative) frequency, while minima will have no imaginary frequencies.
Nf710 (talk) 22:15, 22 March 2018 (UTC) Correct you get this info by diaginalising the hessian in the basis of the normal modes. which are linear combinations of the degrees of freedom. These are the vibrations that you see , when you move along the normal mode vector.
Importance of studying Transition States
When one or more products can be formed, the transition states can be used to predict the product formed. For the formation of kinetic products, the pathway typically follows a lower activation energy and hence more stable transition state favoured.
Diels-Alder Reaction
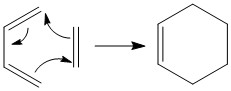
Often referred to as a [4+2] cycloaddition, the Diels-Alder reaction typically occurs between an electron-rich diene and an electron-poor dienophile. This reaction is concerted and occurs via a single cyclic transition state to form a 6-membered ring.
Typically, the reaction occurs where the HOMO of the diene interacts with the LUMO of the dienophile.
In a hetero-Diels-Alder reaction, an inverse electron demand may occur (the diene is more electron-poor than the dienophile). As a result, the main orbitals interacting are the LUMO of the diene and the HOMO of the dienophile.
In reactions where there is a possibility of an endo and exo product in irreversible reactions, the kinetic endo product is preferred over the thermodynamic exo product. This is because the endo transition state is stabilised by orbital, dipolar and Van der Waals interactions between the dienophile and the diene, allowing the reaction to proceed at a faster rate. These stabilising interactions are absent in the exo transition state as the atoms on the dienophile and diene are too far away to interact. However, the exo product is the thermodynamic product due to less clashes in sterics.
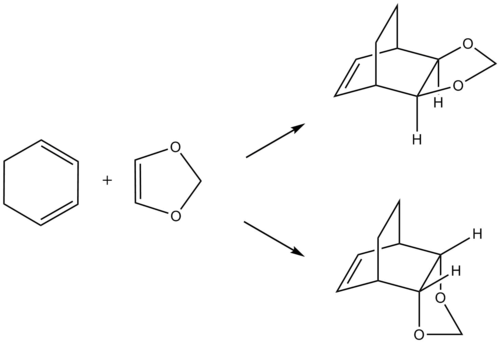
In exercise 1, a simple Diels-Alder reaction between butadiene and ethylene was investigated. In exercise 2, a reaction between cyclohexadiene and 1,3-dioxole was investigated, where the formation of endo and exo adducts have to be further looked at. In exercise 3 involving xylylene and sulfur dioxide, a competing reaction known as Cheletropic reaction may occur.
Gaussview tool used for calculations
Gaussview software was used to analyse the transition structures and calculations were made to predict the reactivity of the reactions. The semi-empirical PM6 method and the Density Function Theory (DFT) B3LYP methods were employed to optimise the structures of the reactants, transition states and products. PM6 is a quicker method as it utilises experimental data to optimise the reaction structures, replacing the two-electron integrals, Coulomb and exchange integrals, which are more difficult to calculate. DFT calculations define the energy of a system as a sum of 6 components, EDFT = ENN + ET + EV + ECoul + EExchange + ECorr.
ENN = nuclear-nuclear repulsion, EV = nuclear-electron attraction, ECoul = electron-electron Coloumb repulsion.
These terms above are the same used in the Hartree-Fock theory. The energies below are different from the terms used in the Hartree-Fock theory as ECorr is not accounted for in the theory.
ET = kinetic energy of the electrons, EExchange = electron-electron exchange energies, ECorr = correlated movement of electrons of different spin.
B3LYP (Becke-3-LFP) is a hybrid method, which mixing exchange energies calculated in an exact manner with those obtained from DFT methods to improve performance.
Nf710 (talk) 22:17, 22 March 2018 (UTC) This is correct however in DFT the exchange and correlation terms are put together into the exchange correlation term, which is unknown and we use different functionals to model it. B3LYP uses HF to get the exact static correlation.
Exercise 1: Reaction between Butadiene and Ethene
(Fv611 (talk) Good job across the whole exercise. Well done!)
Reaction Scheme
Molecular Orbitals
The reactants, cis-butadiene and ethene, as well as the product cyclohexene, and the transition state were optimised using PM6 method. The tables below show the Jmol files for the HOMO and LUMO of the reactants and the 4 MOs that are produced in the transition state (MO 16, MO17, MO18 and MO19). The transition state was then verified using an intrinsic reaction coordinate (IRC). File:JDN15TSIRC.LOG
The HOMO of the electron-rich diene, ethene, and the LUMO of the electron poor dienophile, cis-butadine, interact in this conventional Diels-Alders reaction.
| Butadiene HOMO | Butadiene LUMO | Ethene HOMO | Ethene LUMO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MO 16 | MO 17 | MO 18 | MO 19 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
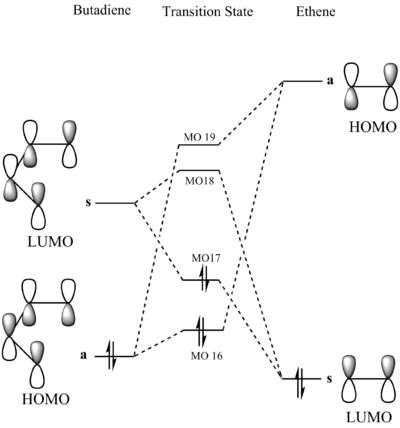
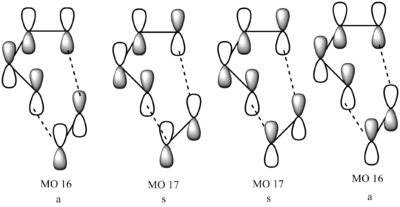
The MO diagram for the transition state is drawn above (s for symmetric and a for anti-symmetric). Only orbitals with the same symmetry (i.e symmetric-symmetric, antisymmetric-antisymmetric) are able to interact as the orbital overlap integral is non-zero. When symmetric orbitals interact with anti-symmetric orbitals, the orbital integral is 0, therefore the overlap is forbidden.
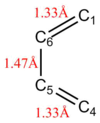
Bond Length Analysis
| Butadiene | Ethene | Transition State | Cyclohexene |
|---|---|---|---|
|

|

|
|
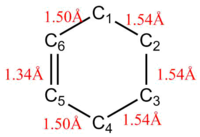
Compared to the starting bonds, it is observed that there is a shortening of the bond length between C5 and C6, from 1.47 Å to 1.41 Å, suggesting a change from single bond to double bond. There is also a lengthening of bonds between C1-C6 and C4-C5, from 1.33 Å to 1.50 Å, suggesting a change from double bond to single bond.
The average sp3 and sp2 C-C bond lengths are 1.54 Å and 1.34 Å respectively. The Van der Waals radius of a C atom is 170 Å. In the transition state, the partially formed C-C bonds between C1-C2 and C3-C4 were 2.11 Å. This is longer than the average sp3 but shorter than twice the Van der Waals radius of the C atom. This highlights that the orbitals are close enough to interact with each other but are not yet able to form a complete C-C bond.
Vibration of Reaction Path at Transition State
The vibration corresponds to the reaction path at the transition state (-949.35cm-1). As ethene is a symmetric dienophile, both C have equal probability to become the electrophilic site. When the reactants are in the correct orientation and position, the formation of the 2 new sigma bonds happen rapidly hence the formation of the two bonds is synchronous.
Exercise 2: Reaction of Cyclohexadiene and 1,3-dioxole
Reaction Scheme
Molecular Orbitals
The reactants, cyclohexadiene and 1,3-dioxole, as well as the product and the transition state were calculated using PM6 method and optimised using B3LYP. The tables below show the Jmol files for the HOMO and LUMO of the reactants. Two sets of MOs are shown as well (MO 40, MO 41, MO 42, MO 43) for both exo and endo transition states.
| Reactants | ||||||
|---|---|---|---|---|---|---|
| HOMO | LUMO | |||||
| Cyclohexadiene | ||||||
| 1,3-dioxole | ||||||
| Transition States | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimised | MO 40 | MO 41 (HOMO) | MO 42 (LUMO) | MO 43 | |||||||||||
| EXO | |||||||||||||||
| ENDO | |||||||||||||||
A MO diagram was constructed from the energy levels of the MOs calculated above. 1,3-dioxole has 2 adjacent O which can donate electron density to the double bond, resulting in an electron-rich dienophile. This increase in electron density increases the energy of both the HOMO and LUMO of the dienophile, where the HOMOdienophile is higher than the HOMOdiene. The HOMOdienophile is closer in energy to the LUMOdiene, hence interacts stronger as compared to the HOMOdiene interacting with the LUMOdienophile. This results in an inverse electron demand Diels-Alder reaction.
(Fv611 (talk) You have presented the same MO diagram with different TS schemes. You should have shows or discussed the differences between exo and endo conformations in terms of their relative MO energies.)
| Exo | Endo |
|---|---|
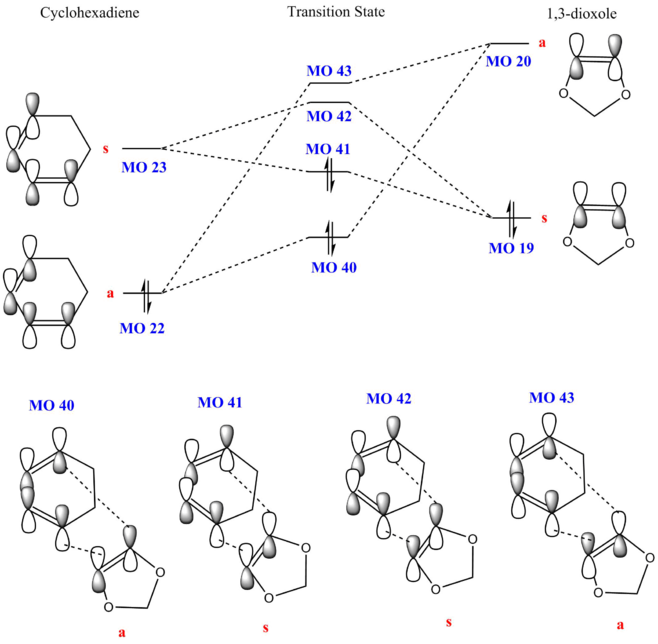
|
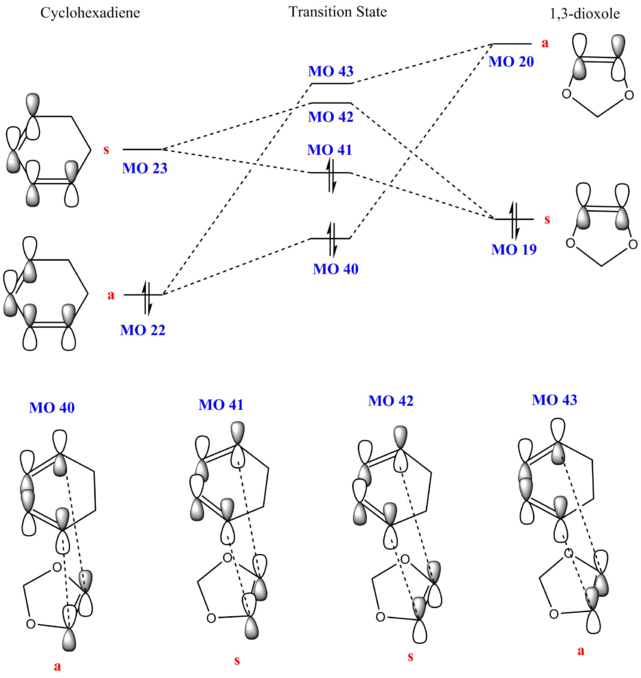
|
Reaction Barrier and and Reaction Energy Calculations
Reaction Barrier = Energy of TS - Total Energy of Reactants
Reaction Energy = Energy of Product - Total Energy of Reactants
| Product | Total Energy of Reactants (ha) | Transition State (ha) | Product (ha) | Reaction Barriers (kJ / mol) | Reaction Energies (kJ / mol) |
|---|---|---|---|---|---|
| EXO | -500.3925 | -500.3292 | -500.4173 | 166 | -65.1 |
| ENDO | -500.3321 | -500.4187 | 158.6 | -68.8 |
| HOMO of Transition States | |||||
| EXO | ENDO | ||||
|---|---|---|---|---|---|
Typically, the exo product is the thermodynamically favoured product as the endo product is likely to have diaxial interactions. However, in this case, it is observed that both exo and endo products have steric clashes. From the table above, we observe that the reaction barrier for the formation of the endo product is lower than the formation of the exo product, suggesting that the endo product is more kinetically favourable. This is due to additional secondary (non-bonding) orbital interaction in the transition state, where the oxygen atoms on the 1,3-dioxole is able to interact with the cyclohexadiene, resulting in a lower transition state energy.
The endo product is also the thermodynamic product, with a lower energy (more negative) than the exo-product. This is likely due to lesser steric clashes in the endo product compared to the exo product.
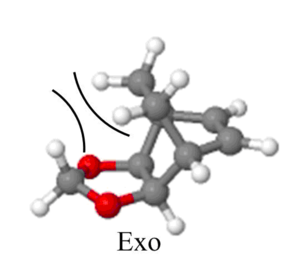
Nf710 (talk) 22:33, 22 March 2018 (UTC) Nice diagram of the sterics. Your energies are correct. But you have only stated that the reaction in inverse with no proof. You can do this quantitatively. There were parts that you could have gone into more detail in.
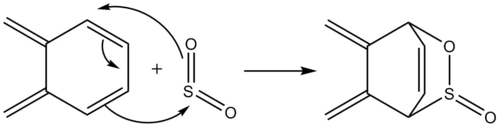
Exercise 3: Diels-Alder vs Cheletropic
Reaction Scheme
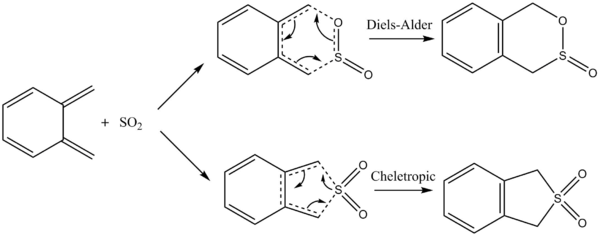
As seen in the reaction Scheme, the reactants are able to react via 2 competing reactions, the Diels-Alder reaction and the Cheletropic reactions.
Reaction Pathways
The reactants, xylylene and SO2, as well as the product and the transition state were optimised using PM6 method.
| xylylene | SO2 | ||||
|---|---|---|---|---|---|
The tables below show the IRC for the EXO Diels-Alder reaction, ENDO Diels-Alder reaction and the Cheletropic reaction.
| Reaction Pathway | Visual Animation | File Logs |
|---|---|---|
| EXO DA Reaction | 
|
File:JDN15EXOTSEIGEN.LOG |
| ENDO DA Reaction | 
|
File:JDN15ENDOTSEIGEN.LOG |
| Cheletropic Reaction | 
|
File:JDN15CHETS2.LOG |
By observing the visual animations of the IRCs, it is observed that the 6 membered ring in Xylyene which originally had 4 sp3 C and 2 sp2 C gained stability by attaining aromaticity after the reaction, forming 6 sp2 C.
(The carbon atoms are all sp2-hybridised in xylylene. The structure forms a resonance with the diradical form (aromatic but still unstable) Tam10 (talk) 13:43, 16 March 2018 (UTC))
Reaction Barrier and Reaction Energy Calculations
Reaction Barrier = Energy of TS - Total Energy of Reactants
Reaction Energy = Energy of Product - Total Energy of Reactants
| Product | Total Energy of Reactants (ha) | Transition State (ha) | Product (ha) | Reaction Barriers (kJ / mol) | Reaction Energies (kJ / mol) |
|---|---|---|---|---|---|
| EXO DA | 0.059417 | 0.092077 | 0.021451 | 85.7 | -99.7 |
| ENDO DA | 0.090559 | 0.021698 | 81.8 | -99.3 | |
| Cheletropic | 0.099062 | 0.000005 | 102.2 | -157.0 |
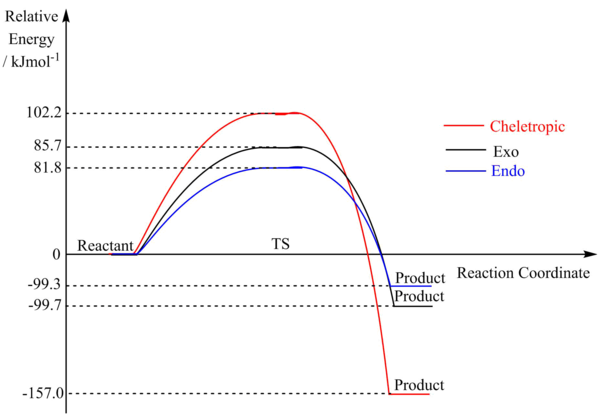
From the table above, a reaction profile for reach of the reactions was constructed.
(Use straight lines for reaction profiles Tam10 (talk) 13:43, 16 March 2018 (UTC))
Based on the data from the table, we can calculate that the Cheletropic product has the lowest energy and hence is thermodynamically favoured. As sulfur is larger than C, the resulting twist in the 6 membered ring in the Diels-Alder products have a ring strain due to inefficient sp3 hybridisation, resulting in a highly distorted structure. This is in comparison to the Cheletropic product, which is able to adopt a planar configuration that maximises the distance between the O and the neighbouring H atoms. However, the Cheletropic reaction also has the highest reaction barrier, suggesting it is the least kinetically favoured pathway. Therefore, it is likely the cheletropic product forms as the major product under high temperatures and long reaction times in equilibrating conditions.
The endo Diels-Alder product is kinetically favoured as it has the lowest reaction barrier. The endo product has a lower reaction barrier than the exo product, which is likely due to additional stabilising interactions between the p orbitals on the O of SO2 and the conjugated π system on xylylene. Therefore, it is likely the endo Diels-Alder product forms as the major product under low temperatures and short reaction times in non-equilibrating conditions.
From the transition state HOMO, we can observe that both the endo and exo TS have stabilising secondary orbital interactions, therefore reducing the reaction barrier in these reactions. This also explains why the energy of the exo and endo TS are relatively close in energy. We can also see that the Cheletropic TS has no stabilising secondary interactions and is highly antisymmetric with many nodes, resulting a higher energy TS.
| Diels-Alder Reaction | Cheletropic Reaction | ||
|---|---|---|---|
| ENDO | EXO | ||
| Transition State
HOMO |
|

|
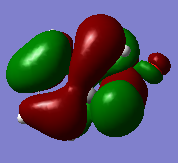
|
(It's pretty hard to see what's going on in these MO pictures. Perhaps use transparent surfaces? Tam10 (talk) 13:43, 16 March 2018 (UTC))
Cis-butadiene Fragment on Xylylene for Reactions
There are 2 cis-butadiene fragments on xylylene which is able to undergo reactions. The outer cis-butadiene is able to undergo Diels-Alder reactions and Cheletropic reactions as seen above, while the inner cis-butadiene fragment is only able to undergo Diels-Alder reaction. However, reaction at this site is highly unfavoured due to steric hinderance and the formation of a strained bicyclic ring. Moreover, this reaction not only provides no aromatic stabilisation to the system, it lowers the conjugated system and hence is highly unfavoured.
| Product | Total Energy of Reactants (ha) | Transition State (ha) | Product (ha) | Reaction Barriers (kJ / mol) | Reaction Energies (kJ / mol) | File Logs |
|---|---|---|---|---|---|---|
| EXO DA 2 | 0.059417 | 0.105054 | 0.067300 | 119.8 | 20.7 | File:JDN15 EXO2 Product.LOG |
| ENDO DA 2 | 0.102070 | 0.065612 | 112.0 | 16.3 | File:JDN15 ENDO2 Product.LOG |
Comparing the values from the table, we can see that both exo and endo for this Diels-Alder reaction has a much higher reaction barrier than the previous reactions (discussed earlier). Hence the secondary Diels-Alder reactions are the least kinetically favourable. We can also see that the reaction energies of the secondary Diels-Alder reactions are positive, indicating that the reaction is highly thermodynamically unfavourable as ΔG>0 and hence the reaction is not spontaneous.
Conclusion
Gaussian is a useful method to carry out molecular geometry optimisations and calculations. By investigating the free energies of the transition states and products, we can determine the reaction energies and reaction barriers of the reaction. We can then determine which reactions are kinetically or thermodynamically favoured. This computational method is a powerful tool that can be used for preliminary research before testing out the reactions experimentally. It also provides a visual representation that allows better understanding on the interactions between the MOs of the molecules before, during and after the reaction.
