Rep:MOD:Ct1515 TS
TRANSITION STATES AND REACTIVITY
INTRODUCTION
Potential Energy Surfaces & Transition States
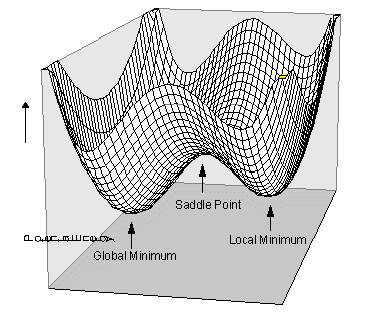
A potential energy surface (PES) describes the different potential energies of different conformations of molecules involved in a reaction on a 3D surface. An example can be seen in Figure 1. The degrees of freedom of a PES corresponds to the amount of nodes of the reaction. They usually will have a maximum where the energy is at its highest, a first order saddle point, this is usually its transition state and a minimum where the product exists in its lowest energy conformation.
There is a possibility of a global and local minima. The global minima is the point on the PES where the molecule(s) is at it's lowest energy. A local minima is that of a minimum of energy without having to overcome another activation barrier to achieve the global maxima; a low point of energy but not the lowest on the graph. At the maximum and minimum the 1st derivative of the curve is zero but the 2nd derivative is less than zero for a maximum and greater than zero for a minimum. During this report the Transition states of Diels-Alder reaction will be investigated.
Nf710 (talk) 09:26, 11 January 2018 (UTC) A first order saddle may not be the highest point on a PES. On an N dimensional PES there may be higher order saddle points of higher energy. You also haven't described a TS or minimum on a 3N-6 degrees of freedom dimensional PES. A minimum will have the second derivatives for all dimensions positive. A TS will have all positive except 1 which is the reaction coord. You can get this info from the Hessian matrix eigenvalues.
The Diels-Alder reaction
This project investigated certain Diels-Alder reaction, a concerted combination of a diene and dienophile to form a ring structure. The 4+2 cycloadditions can either take one of two routes, via an exothermic (exo) or endothermic (endo) transition state depending on the way in which the reacting molecules collide. The transition states have a corresponding energy and are different for the exo and endo approach due to the different conformations of the transition states.
For a reaction to be able to take place the orbitals must be of similar energy in order that they can interact in order to react. In a normal Diels-Alder reaction the LUMO of the dienophile and the HOMO of the diene are of the same symmetry these orbitals are the ones that must be of similar energy. An inverse Diels-Alder reaction can also take place when the HOMO of the dienophile is higher in energy than that of the HOMO of the diene, usually due to the presence of an electron withdrawing group on the dieneophile.
In this investigation the relative energies of the orbitals of the transition states were investigated. The overall energy of the structures were also investigated and compared.
Computational Methods used in Investigation
Gaussian was the program used to investigate the properties of a reaction scheme. It uses different quantum mechanical methods to be able to determine these reaction co-ordinates depending on the level of accuracy required. The two methods used in this investigation was the semi-empirical PM6 (Parameterization Method 6) method and the DFT hybrid B3LYP method with the basis set of 6-31G(d).
Most computationl methods are based on or have some contribution from the Hartree-Fock method where the molecular orbitals are made with a linear combination of atomic orbitals, that is to say slater determinants.
Density Functional Theorem (DFT) is similar to the Hartree-Fock method by the fact it describe the quantum states of a many-electron system and also uses the the Born-Openheimer approximation within its calculations. However instead of using a linear combination of the orbitals it uses electron density to calculate the energies of the molecule.
Nf710 (talk) 09:30, 11 January 2018 (UTC) Some confusion here. All the methods calculate a quantum state with varying degreees of approximation. DFT can only calculate the ground state. And all Quantum chemistry methods use the BO approx.
The hybrid functionals combine the two theorems to a more accurate solution to getting the correct energies.
The basis set used in this experiment was the 6-31G(d) level. This is a set of linear combinations of one-partical functions which are used to describe the molecular orbitals. The 6-31G(d) is explained as followed, a linear combination of 6 gaussion functions were used to describe the inner shells.[2] The 31 describes the number of primitives used to describe the valence shells. It is a double-zeta basis meaning it uses 2 basis functions per atomic orbital within the molecule. The "d" represents the polarization of the orbitals and allows d character to impact the orbitals. The polarisation is key in the calculations involving larger molecules and also reacting molecules due to the fact that it takes into account uneven distribution of electrons about a bond due to different electronegativity and also breaking and making of bonds.[3] Semi-empirical methods are based on the Hartree-Fock solutions to the optimisation however they also take some data from experimental sources to help minimise the computational cost of the optimisations.
Nf710 (talk) 09:30, 11 January 2018 (UTC) This is a really good understanding of the basis sets well done. So equations could have complemented the discussion.
In exercise 1 and 3 the PM6 levels were sufficient however in exercise 2 the DFT B3LYP 6-31G(d) was used to obtain more accurate results.
Procedure to find the Transition State
The main method used to find the transition state involved first optimising the reactants individually. The second step was optimising and running frequency calculations of them together freezing the bond between the reacting atoms at a reasonable distance apart. To check that this structure was going to be a transition state the vibrational frequencies were checked for one negative frequency corresponding to the formation of the bond. Thirdly, the structure was then optimised to a transition state again checking for that negative frequency. The final step was to run an Intermediate Reaction Co-ordinate (IRC) in order to check that the reaction would go to completion and therefore the transition state structure be correct.
For exercise three specific bond lengths were adjusted in the second steps in order that the correct reaction occurred.
Exercise 1
(Fv611 (talk) Very good, concise discussion across the whole exercise. Well done!)
1,3-Butadiene and Ethene
During this exercise the Diels-Alder reaction of 1,3-Butadiene and Ethene were investigated. It is a π4s + π2s cycloaddition reaction that give cyclohexene. The reactants, transition state and products were all optimised at a PM6 level and conduction of a frequency calculation and an IRC for the transition state was done to confirm the presences of a true transition state. The presence of only one negative vibration frequency (and imaginary frequency) and the correct IRC pathway confirmed the presence of the transition state.

Molecular Oribtal Visualisations of Reactants
The visualisation of the Molecular Orbitals (MOs) for the reactants can be found in the JMOLs added below.
|
|
MO Diagram for the reaction between 1,3-Butadiene and Ethene
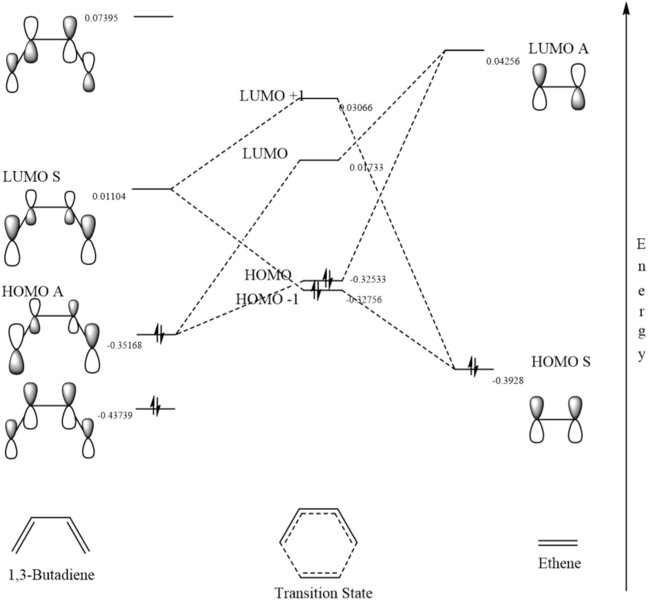
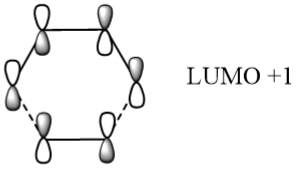
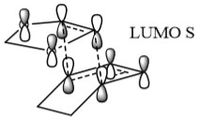
In Figure 3 the MO diagram for the reaction can be seen. Basic symmetry labels have been added to the orbitals which show the composite MOs which make up the overall MO at each stage. Due to the energies of the orbitals, the key interaction of orbitals is that of the the HOMO of the diene with the LUMO of the dieneophile making it a normal Diels-Alder reaction.
JMOL of Transition State of the reaction
Below is the JMOL of the optimised transition state at the PM6 level where the molecular orbitals that participate in the reaction can be visualised.
Transition state |
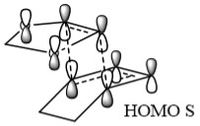
Table 2 below shows a frozen image of the PM6 level optimised transition state orbitals in the HOMO+1, HOMO, LUMO & LUMO-1 states.
Table 2 also shows the corresponding atomic orbitals that are used to make up these optimized transition state orbitals. They also correspond to the same named orbitals in the MO diagram in Figure 3.
The reacting orbitals must have the same symmetry in order to react. This is so that the orbital overlap integral is non-zero, that is to say there is some form of overlap between the reacting molecules. Symmetric-Asymmetric orbital overlaps are forbidden due to the fact that this integral becomes zero and therefore are not overlapping. However asymmetric-asymmetric and symmetric-symmetric orbital interactions lead to reaction as there is a non-zero orbital overlap integral.
Investigation of Bond length change during the reaction

Table 3 shows the change in bond length over the course of the reaction. The labelled carbons correspond to the carbons labelled in Figure 4.
| Carbon-Carbon Bond | Reactants (Å) | Transition State (Å) | Product (Å) |
|---|---|---|---|
| C1 to C2 | 1.33534 | 1.37970 | 1.50034 |
| C2 to C3 | 1.46848 | 1.41114 | 1.33766 |
| C3 to C4 | 1.33534 | 1.37979 | 1.50034 |
| C4 to C5 | 2.11412 | 1.54003 | |
| C5 to C6 | 1.32731 | 1.38173 | 1.54076 |
| C6 to C1 | 2.11526 | 1.54003 |
| Description | Length (Å) |
|---|---|
| Typical sp2 hybridsed C-C bond | 1.3 |
| Typical sp3 hybridsed C-C bond | 1.5 |
| VDW Radius of carbon | 1.7 |
During this reaction it can be seen in Table 3 that the bond between C1 and C2, C3 and C4 and C6 and C5, ie the sp2 hybridised carbons, elongated as they changed from a a double to a single bond during the reaction. The forming alkene bond between C2 and C3 can be seen to shorten as it changes from sp3 hybridised character to sp2 character.
In the transition state the bond length between the forming bond is less that 2 VDW radii away from each other meaning that the orbitals will be interacting. It is longer than a typical single bond so in the transition state the bond hasn't completely formed.
In the product molecule the bond lengths between each of the carbons are close to their corresponding bond typical lengths. This is to say that the bonds of around 1.5Å are all sp3-sp3 hybridised and the onle sp2-sp2 hybridised bond between C2 and C3 is close to 1.3Å.
Imaginary/Negative Vibrational Frequencies in the Transition State
In the frequency analysis of the optimised transition state structure a one negative frequency appears. This frequency corresponds to the formation of the new bonds in the product molecules. This vibration is shown in the gif in Figure 5. As the formation of the 2 bonds is at the same time it can be describes and a synchronous reaction.
Exercise 2
Cyclohexadiene and 1,3-Dioxole
In Exercise 2 an investigation of the reaction between Cyclohexadiene and 1,3-Dioxole was undertaken. The reactants, transition state and products were all optimized at the B3LYP level using the basis set of 631G-(d). And IRC at the PM6 level was also conducted in order to see whether the transition state was correct and to investigate the two reaction pathways.

In Figure 6 the two reaction pathways are shown, the exothermic (exo) and endothermic (endo) routes, in which the reaction can proceed. The resulting product depends on the trajectory of the reacting molecules and their position in regards to one another. The exo route has the oxygen atoms in the dioxole facing away from the sp2 bond in the cyclohexadiene. The endo pathway has the oxygen atoms over the top of the sp2 hybridized bond and this therefore means an interaction can take place between the p orbitals of the oxygen and the π orbital stabilizing the transition state. This is what's known as secondary orbital interactions when stabilisation occurs but not through the bonding orbitals.
MO diagram of exo and endo pathways
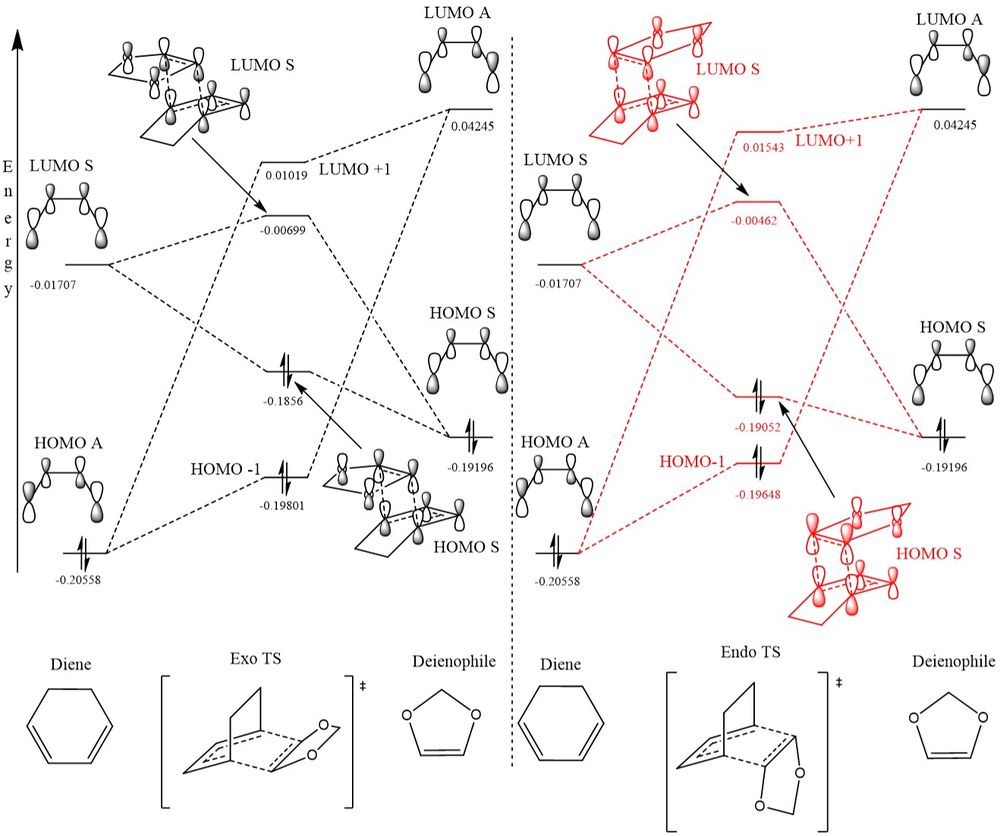
(Fv611 (talk) Very nice MO diagrams. Could have pushed your discussion on exo vs endo a tiny bit more (you're almost there!) by expliciting that your calculated MO energies show the stabilisation due to secondary orbital interactions in one case but not the other.)
This reaction is an inverse Diels-Alder reaction due to the fact the HOMO of the dieneophile is higher in energy than the HOMO of the diene. This is due to the presence of the electron withdrawing goup (the oxygen atom) adjacent to the reacting alkene bond. The orbitals of same symmetry therefore is the LUMO of the diene and HOMO of the dienophile and therefore is the allowed orbital interaction. Interactions between the HOMO of the diene and LUMO of the dienophile also take place due to them having the same symmetry.
MO analysis
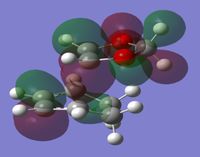
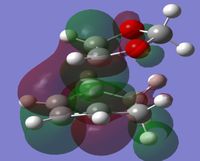
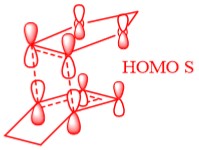
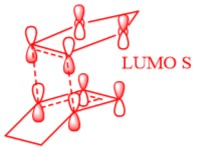
In Table 5 a frozen image of the transition state molecular orbitals can be found. These correspond to the same labelled molecular oribitals in the Molecular Orbital Diagram in Figure 7.
The secondary orbital interactions of the Endothermic Reaction can be clearly seen in the HOMO of the transition state as there is significant overlap between the oxygen's p orbitals and the π orbital of the diene.
JMOL for the Transition States
|
|
Nf710 (talk) 09:35, 11 January 2018 (UTC) You could have increased the ISO value to show more of the SOO.
Thermochemistry
Table 7 shows the Sum of electronic and thermal Free Energies of the reactants, transition states and the products of the endo and exo reactions.
| Molecule | Energy (Hartrees) | Energy (kJ mol-1) |
|---|---|---|
| Cyclohexadiene (reactant) | -233.321033 | -612584.4188 |
| 1,3-Dioxole (reactant) | -267.068145 | -701187.4681 |
| Combined Reactant Energy | -500.389178 | -1313771.8869 |
| Exo Transition State | -500.329163 | -1313614.3175 |
| Endo Transition State | -500.332149 | -1313622.1573 |
| Exo Product | -500.417322 | -1313845.7790 |
| Endo Product | -500.418691 | -1313849.3733 |
From their the activation energy of the reaction can be calculated along with the energy of the reaction. The activation energy was calculated by the equation (energy of transition state)-Σ(energy of reactants). The energy of the reaction was calculated as Σ(energy of reactants) - Σ(energy of products).
| Type of reaction path | Activation Energy (kJ mol-1) | Energy of the Reaction (kJ mol-1) |
|---|---|---|
| Exothermic Route | 157.57 | -73.89 |
| Endothermic Route | 149.73 | -77.49 |
What can be determined from the calculated energies is that the Endothermic route has a lower activation energy. This is as predicted due to the secondary orbital interactions. It is therefore the kinetic product of the reaction. When comparing the energies of the products it is also true that the endothermic product is lower in energy and therefore a more stabilised molecule. It this therefore the thermodynamic product as well.
Nf710 (talk) 09:40, 11 January 2018 (UTC) Your energies seect o be 10 outKJ out for all values. Maybe you calculated your Reactant incorrectly? However you have still come to the correct conclusions. Your diagrams and jmols of SOO are nice. You could have investigated the electron demand quantitatively by doing an energy calculation with both reactants in the same potential energy surface and then looking at the orbitals.
Exercise 3
Xylylene and SO2
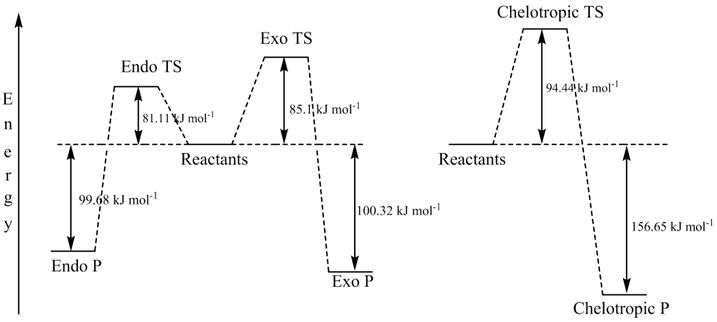
In this exercise the reaction between Xylylene and SO2 was investigated. As shown by Figure 8 there were three routes investigated, that of the endo and exo reactions and also of the chelotropic reaction. The reactants, transition states and products were all optimised using the semi-empirical PM6 method and an IRC was calculated for each of the three reaction pathways.

(Endo and exo are not abbreviations for "endothermic" and "exothermic". They just mean "inside" and "outside". You are also not using wedges in your diagram properly Tam10 (talk) 12:19, 9 January 2018 (UTC))
All reaction pathways are cycloadditions. The endo and exo reactions are a 4+2 cycloaddition reactions. The distinguishing factor of the chelotropic reaction is that both the new bonds are being formed to the same atom.
Visualisation of the three reaction Pathways
Below the reaction pathway taken can be seen in the animations.
The exo and endothermic reactions are both asynchronous as the bond with the oxygen forms with the carbon before the bond with the sulphur. The chelotropic reaction is however synchronous as the bonds form at the same time.
(Be careful here when saying the C-O bond is formed first. Gaussview uses distance cut-offs to determine whether a visual "bond" should be drawn, but it is not exact Tam10 (talk) 12:19, 9 January 2018 (UTC))
Xylylene is a very unstable molecule due to its lack of aromaticity across the molecule. Upon reaction in each of these pathways the product molecule has an aromatic 6 membered ring which greatly stabilises the overall molecule. This is therefore one of the driving forces for the reaction. This can be seen in each of the IRC animations, as the bond lengths and type of bonds change within the reactants to products. The double bond elongates to become an intermediate length between single and double bond character, characteristic of an aromatic C-C bond length in a six membered ring.
Thermochemistry
In Tables 10&11 the energy levels of the different molecules involved in the different reaction pathways was investigated.
| Molecule | Energy (Hartrees) | Energy (kJmol-1) |
|---|---|---|
| Xylylene (reactant) | 0.178279 | 468.072 |
| SO2 (reactant) | -0.118614 | -311.421 |
| Combined Reactant Energy | 0.059665 | 156.651 |
| Exo Transition State | 0.092077 | 241.748 |
| Endo Transition State | 0.090559 | 237.763 |
| Chelotropic Transition State | 0.099062 | 260.087 |
| Exo Product | 0.021455 | 56.330 |
| Endo Product | 0.021702 | 56.979 |
| Chelotropic Product | 0.000000 | 0.000 |
| Type of reaction path | Activation Energy (kJ mol-1) | Energy of the Reaction (kJ mol-1) |
|---|---|---|
| Exothermic Route | 85.10 | -100.32 |
| Endothermic Route | 81.11 | -99.68 |
| Chelotropic Route | 94.44 | -156.65 |
From these energies it can be noted that the reaction with the lowest activation barrier is the endothermic reaction. This is therefore the kinetic product of the reaction. The exothermic pathway gives a product with lower energy and therefore is the thermodynamic product.
When comparing all three however the chelotropic reaction has the lowest energy products.
(Can you think of why this might be? Tam10 (talk) 12:19, 9 January 2018 (UTC))
Further Investigation
An investigation of the reaction of the other cis-butadiene molecule in the Xylylene was investigated and a comparison of the energies was under taken.
 |
 |
| Molecule | Energy (Hartrees) | Energy (kJmol-1) |
|---|---|---|
| Combined Reactant Energy | 0.059665 | 156.651 |
| Exo Transition State | 0.105052 | 275.814 |
| Endo Transition State | 0.102071 | 267.987 |
| Exo Product | 0.067304 | 176.707 |
| Endo Product | 0.102074 | 267.995 |
| Type of reaction path | Activation Energy (kJ mol-1) | Energy of the Reaction (kJ mol-1) |
|---|---|---|
| Exothermic Route | +119.163 | +20.056 |
| Endothermic Route | +111.336 | +111.344 |
This therefore means that the products have a higher energy than the reactants and therefore means that this reaction is very thermodynamically unstable.
Conclusion
Diels-Alder reactions and their transition states were investigated conducted using PM6 and B3LYP (6-31G(d)) computational methods.
The first reaction was Butadiene and Ethene to form cyclohexene. This reaction was a normal Diels-Alder reaction with synchronous bond formation.
The second reaction was that of cyclohexadiene and 1,3-Dioxole. This reaction was an inverse Diels-Alder due to the electron withdrawing group of oxygen.This reaction went via two routes and exo and endothermic route. Due to secondary orbital interaction the endo product had a lower activation energy and lower product energy and was therefore the favoured thermodynamic and kinetic study.
For the first and second reaction an investigation of the transition state molecular orbitals was undertaken.
The third reaction was that of SO2 and Xylylene. This was mainly a comparison of the Diels-Alder against the chelotropic reaction. The Diels-Alder endothermic product had the lowest activation energy and was therefore the kinetic product. The chelotropic products were the lowest in energy of the three but the very large reaction barrier energy meant this reaction was unlikely to occurr.
A further investigation of a Diels-Alder reaction of the SO2 at the other diene site showed that the products were higher in energy than the reactants and was therefore a very unfavourable reaction.
Appendix
Exercise 1 (log files)
Butadiene (Opt to Minimum (reactant)) PM6
Ethene (Opt to Minimum (reactant)) PM6
Cyclohexene (Opt to minimum) PM6
Exercise 2 (log files)
Cyclohexadiene (Reactant) B3LYP
Exercise 3 (log files)
Futher investigation (log files)
References
- ↑ https://sites.google.com/site/janroshijakubik/my-research/molecular-modelling/potential-energy-surface (visited on 18/12/2017)
- ↑ Ditchfield, R; Hehre, W.J; Pople, J. A. (1971). "Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules". J. Chem. Phys. 54 (2): 724–728. Bibcode:1971JChPh..54..724D. doi:10.1063/1.1674902.
- ↑ Ditchfield, R; Hehre, W.J; Pople, J. A.(1972). "Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules" . J. Chem. Phys. 56, 2257; https://doi.org/10.1063/1.1677527