Rep:MOD:CID01260105

NH₃

Molecular Information

Category	Information
N - H Bond Length	1.01798Å
H-N-H Bond Angle	105.741°
Calculation Method	R3BLYP
Basis Set	6-31(d,p)
E(R3BLYP)	-56.55776873 a.u.
RMS Gradient Norm	0.00000485 a.u.
Point Group	D_∞h
Calculation Log	NH₃ Optimisation

NH3 Molecule

Convergence Confirmation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986292D-10
 Optimization completed.
    -- Stationary point found.

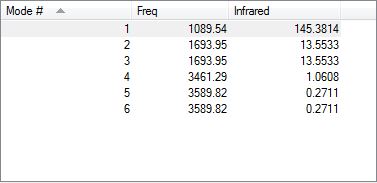
Vibrational Data

i) Given that there are 4 atoms in this non-linear molecule, N=4, 3N-6 = 12-6 =6. Thus 6 vibrational modes were expected and found

ii) There are two pairs of degenerate bond vibrations listed at Mode # 2-3 and 5-6

iii) The bending vibrations are Modes: 1, 2 and 3. The stretching vibrations are 4, 5 and 6.

iv) Mode #4, (Frequency:3461.29) is the most highly symmetric vibration

v) Mode #1 (Frequency:1089.54) is the "umbrella" mode due to its resemblance of an umbrella being pushed inside out

vi) Two IR absorption bands are expected. Mode # 4, 5 & 6 have very low intensities (1.0608, 0.2711 and 0.2711 respectively); these will only produce negligible peaks on an IR spectrum. As mentioned, Mode # 2 & 3 are degenerate, producing a single band. This results it 2 absorption bands.

Charge Analysis

With the central atom in NH₃ being the most electronegative, it is expected that the N atom would have the most negative charge/highest electron density. Given that there are three identical monoatomic substituents (three H atoms, all in the same environment), each of these will have the same electron density. Additionally, given the neutral nature of the molecule, the sum of the partial charges on the four atoms must equal -1.125 +3(0.375) = 0

H₂

Molecular Information

Category	Information
H - H Bond Length	0.74279Å
Calculation Method	R3BLYP
Basis Set	6-31(d,p)
E(R3BLYP)	-1.17853936 a.u.
RMS Gradient Norm	0.00000017 a.u.
Point Group	D_∞h
Calculation Log	H₂ Optimisation

H2 Molecule

Convergence Confirmation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-1.164080D-13
 Optimization completed.
    -- Stationary point found.

Vibrational Data

A 0 value occurs for the IR intensity due to the lack of change in dipole moment (given the diatomic molecule)

N₂

Molecular Information

N ≡ N Bond Length = 1.10550Å

Calculation Method: R3BLYP

Basis Set: 6-31G(d.p)

E(R3BLYP) = -109.52412868 a.u.

RMS Gradient Norm = 0.00000217 a.u.

Point Group: D_∞h

Calculation Log: Media:JJ1516_N2_OPTIMISED.LOG

N2 Molecule

Convergence Confirmation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000001     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-4.428717D-12
 Optimization completed.
    -- Stationary point found.

Vibrational Data

As with the diatomic H₂ molecule, there is no change in the dipole moment due to the N - N bond vibration; the molecule is IR inactive, hence the 0 intensity value.

Reaction Energies

Haber-Bosch Process

N_2(g) + 3H_2(g) → 2NH₃

E(NH₃) = -56.55776873 a.u.

2*E(NH₃) = -113.11553746 a.u.

E(N₂) = -109.52412868 a.u.

E(H₂) = -1.17853936 a.u.

3*(H₂) = -3.53561808 a.u.

ΔE = 2*E(NH₃)-[E(N₂)+3*E(H₂)]= -0.0557907 a.u. = -146.48 kJ•mol^-1

ΔE_{(literature value)} = -45.94 ± 0.35 kJ•mol^-1 ^[1]

ΣE_(reactants) = -113.05974676 a.u.

ΣE_(products) = -113.11553746 a.u.

The value and (negative) sign of ΔE indicate that the products (2 molecules of NH₃) are more thermodynamically stable than the reactants (3 molecules of H₂ and one molecule of N₂). Therefore, the Haber-Bosch Process is highly exothermic.

The large discrepancy between the calculated and experimental ΔE values arises chiefly due to the method of energy calculation employed. The computational procedure used by GaussView relies primarily upon Density Functional Theory; the approximations invoked by DFT when dealing with quantum mechanical electron interactions (e.g. exchange and correlation interactions) cause the computed data to differ from real-world, experimental results.

F₂

Molecular Information

Category	Information
F - F Bond Length	1.40317Å
Calculation Method	R3BLYP
Basis Set	6-31(d,p)
E(R3BLYP)	-199.49825217 a.u.
RMS Gradient Norm	0.00008442 a.u.
Point Group	D_∞h
Calculation Log	F₂ Optimisation

F2 Molecule

Convergence Information

         Item               Value     Threshold  Converged?
 Maximum Force            0.000146     0.000450     YES
 RMS     Force            0.000146     0.000300     YES
 Maximum Displacement     0.000180     0.001800     YES
 RMS     Displacement     0.000254     0.001200     YES
 Predicted change in Energy=-2.627106D-08
 Optimization completed.
    -- Stationary point found.

Vibrational Data

As with the diatomic N₂ molecule, there is no change in the dipole moment due to the F - F bond vibration; the molecule is IR inactive, hence the 0 intensity value.

Charge Analysis

Due to the diatomic nature of the molecule, there is no electronegativity difference between the two atoms.

Thus, F₂ is a perfectly covalent molecule, thus the partial charges on the two atoms is 0.

Molecular Orbital Analysis

MO	Plot	Description
1s - 1s σ		This molecular orbital is very low in energy (-24.79732 a.u.). As is evident by the absence of electron density between the two atoms, there is a complete lack of atomic orbital/1s-1s overlap. The 1s orbital in fluorine is very small and very tightly held by the nucleus and thus, it has very little involvement in bonding as seen by this MO diagram.
1s - 1s σ*		This is the antibonding MO which arises from the out-of-phase combination of the 1s AOs from each atom. This σ* orbital is only very slightly higher in energy than the corresponding σ orbital (~0.18kJ•mol^-1), due to the very minor energy-lowering effect which bonding has on the constituent AOs.
2s - 2s σ		There is significant overlap between the 2s orbitals of each atom to form this sigma MO, such that one continuous surface is seen on the MO diagram. The energy of this MO (-1.33642 a.u.) is much higher than that of the 1s-1s σ MO as it is the valence (as opposed to inner shell) electrons of each fluorine atom which populate this (and all higher energy) MOs.
2s - 2s σ*		This is the antibonding MO formed from the out-of-phase combination of the two, 2s AOs. There is a clearly visible nodal region between the lobes of the MO and also notable deformation of the lobes (i.e. they are squashed spheres) due to the repulsion between the two opposite-phase lobes. In contrast to the 1s - 1s σ/σ* MOs, there is a significant energy difference between the 2s - 2s σ/σ* MOs (~645.51kJ•mol^-1) due to the much greater degree of 2s - 2s overlap.
LUMO
LUMO		The LUMO of the F₂ molecule is a 2p - 2p π* antibonding MO (of which there are also two others, all orthogonal to each other). Though this is unoccupied, this MO is still negative in energy (-0.12704 a.u.). Populating this MO will result in the dissociation of the F₂ molecule.

References

↑ Cox, Wagman, et al., 1984 Cox, J.D.; Wagman, D.D.; Medvedev, V.A., CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., New York, 1984, 1

[Haber-1] Cox, Wagman, et al., 1984 Cox, J.D.; Wagman, D.D.; Medvedev, V.A., CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., New York, 1984, 1

[1]