Rep:MOD:ALEXGS

EX₃ Revision Activity

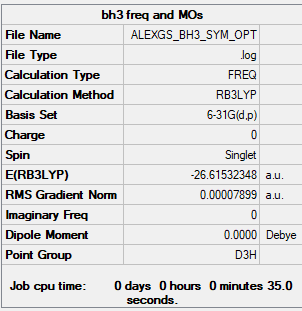
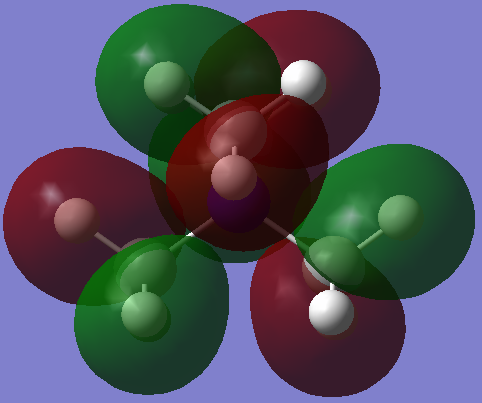
BH₃

Borane

B3LYP/6-31G(d,p) level

         Item               Value     Threshold  Converged?
 Maximum Force            0.000158     0.000450     YES
 RMS     Force            0.000079     0.000300     YES
 Maximum Displacement     0.000622     0.001800     YES
 RMS     Displacement     0.000311     0.001200     YES
 Predicted change in Energy=-1.474609D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis Output File: Media:ALEXGS BH3 SYM OPT.LOG

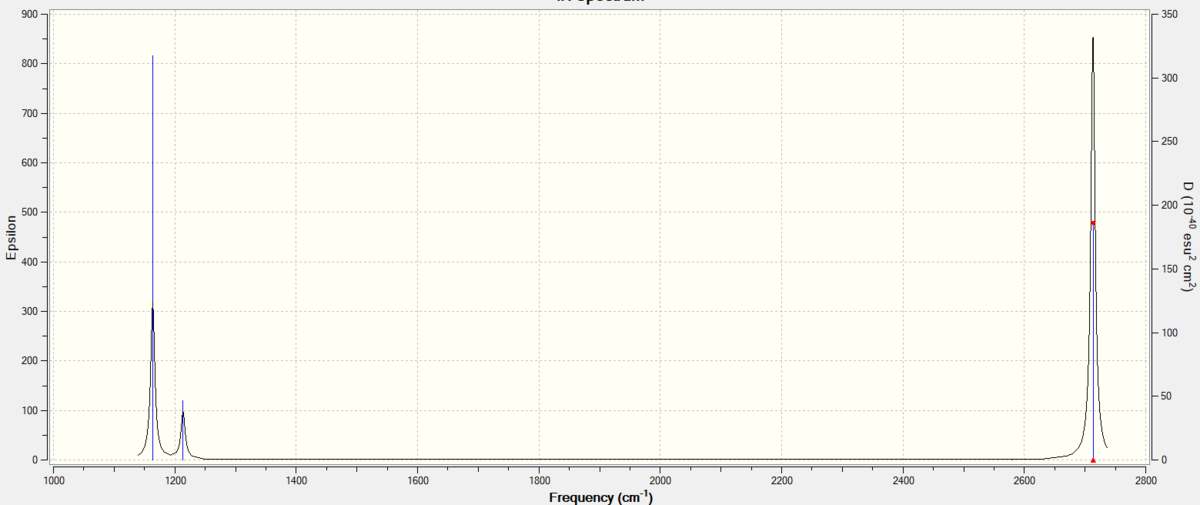
 Low frequencies ---   -0.2456   -0.1129   -0.0054   44.0270   45.1846   45.1853
 Low frequencies --- 1163.6049 1213.5924 1213.5951

Optimised BH Molecule

wavenumber cm-1	Intensity (arbitrary units)	Symmetry	IR active?	Type
1164	92	A2	Yes	Bend, out-of-plane
1214	14	E'	Yes	Bend
1214	14	E'	Yes	Bend
2580	0	A1'	No	Stretch, symmetric
2713	126	E	Yes	Stretch, asymmetric
2713	126	E	Yes	Stretch, asymmetric

Despite they're being 6 different vibrations in the table above, there is only 3 peaks in the IR Spectrum below. This is because the symmetric stretch at 2580cm^-1 isn't IR active because the vibration doesn't cause a change in dipole moment for the molecule. Moreover, the 2 E at 2713cm^-1 stretches are degenerate so their peaks overlap and come up as 1 is in the IR. The same idea applies to 2 E' bends at 1214cm^-1.

Edited from .

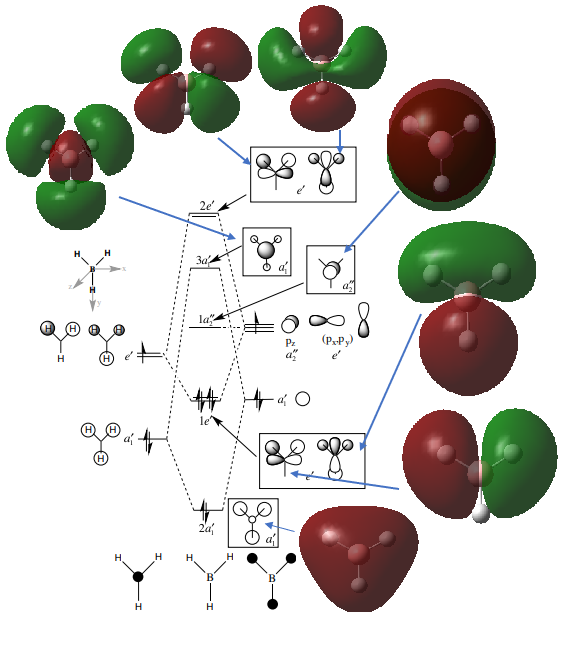
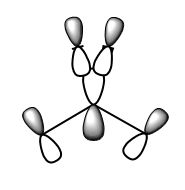
As you can see in the above diagram comparing the Linear Combination of Atomic Orbitals (LCAO) and the Molecular Orbitals (MOs) generated by Guassian, the qualitative MO theory gives a relatively good approximation to the real MOs. Some of the orbitals, for example 1a₂', have been shown from the wrong orientation but still follow the general rule. The qualitative approach is particularly good at showing where the nodes for the orbitals are. However the main difference is that in the LCAO approach leaves empty space in between the AOs whereas the Guassian approach merges the AOs to only leave empty space where there is nodes as discussed above. Moreover, some of the MOs from the LCAOs (3a₁' and the right one of 2e') have a wrong relative proportion or orbital coefficients of the 2 constituent AOs. This is because this approach simplifies this by saying that the AO closest in energy to the MO gives the largest contribution and is therefore 'bigger'. Whereas in reality, the factors contributing to the coefficient are much more complex and this is where the Guassian calculation if useful in predicting the shape of the MOs.

Excellent consideration to both the similarities and the differences between the LCAO and calculated MOs with the use of the 3a₁' and 2e' orbitals as examples. Smf115 (talk) 10:11, 30 May 2019 (BST)

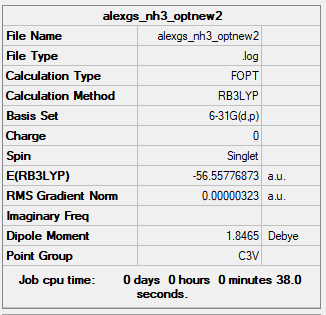
NH₃

Ammonia

B3LYP/6-31G(d,p) level

Item               Value     Threshold  Converged?
 Maximum Force            0.000013     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000039     0.001800     YES
 RMS     Displacement     0.000013     0.001200     YES
 Predicted change in Energy=-3.862150D-10
 Optimization completed.
    -- Stationary point found.

Frequency Analysis Output File:Media:ALEXGS NH3 OPTNEW2 FREQ.LOG

Low frequencies ---   -8.5646   -8.5588   -0.0047    0.0454    0.1784   26.4183
 Low frequencies --- 1089.7603 1694.1865 1694.1865

Optimised NH Molecule

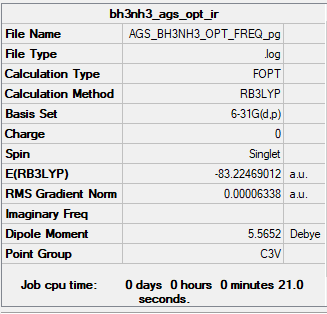
NH₃BH₃

NH₃BH₃ Adduct

B3LYP/6-31G(d,p) level

 Item               Value     Threshold  Converged?
 Maximum Force            0.000114     0.000450     YES
 RMS     Force            0.000062     0.000300     YES
 Maximum Displacement     0.000701     0.001800     YES
 RMS     Displacement     0.000431     0.001200     YES
 Predicted change in Energy=-1.783463D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis Output File:Media:AGS BH3NH3 OPT FREQ.LOG

Low frequencies ---    0.0009    0.0010    0.0012   18.0575   28.4116   40.0963
Low frequencies ---  266.4888  632.3850  639.5950

Optimised NHBH Molecule

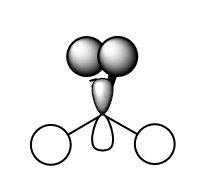
Association Energy Calculation

ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
E(BH3)= -26.61532 a.u.
E(NH3)= -56.55776 a.u.
E(NH3BH3)= -83.22469 a.u.
ΔE= -83.22469- (-26.61532-56.55776)= -0.05161 a.u.= -135.50207 kJ mol-1= -135.5 kJ mol-1

The difference in energy for this reaction is equivalent to the strength of the B-N dative bond because it is the only chemical difference between the products and reactants; the B-N dative bond has a dissociation energy of 135.5 kJ mol^-1. This is in much less than the strength of a typical C-N bond, 305 kJ mol^-1., and equivalent to a very strong hydrogen bond, which vary from 1-161.5 kJ mol^-1 in HF₂^-. Taking these into account, the B-N dative bond would be best assigned as a weak to medium strength bond.

Great evaluation of the bond strength with considered and referenced comparisons. Correct calculation, just be sure to think about the accuracy of your final reported energy values (nearest 1 kJmol^-1). Smf115 (talk) 10:14, 30 May 2019 (BST)

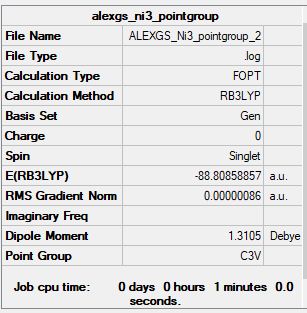
NI₃

Nitrogen tri-Iodide

B3LYP/6-31G(d,p) level

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000010     0.001800     YES
 RMS     Displacement     0.000007     0.001200     YES
 Predicted change in Energy=-2.883030D-11
 Optimization completed.
    -- Stationary point found.

Frequency Analysis Output File:Media:ALEXGS_NI3_POINTGROUP_2_fri_freq.LOG

 Low frequencies ---   0.0010   0.0011  0.0013 35.2977  35.2977   35.2977
 Low frequencies --- 217.4078 316.4871 316.4871

Optimised NI Molecule

The Bond Length of the N-I bonds in these molecules is 2.18936 Angstroms.

Good implementation of the pseudopotential, you needed to include the frequency calculation, however, and not the optimisation log file and the same goes for the summary tables in the structure information. Overall, good first section though! Smf115 (talk) 10:17, 30 May 2019 (BST)

Ionic Liquids Project

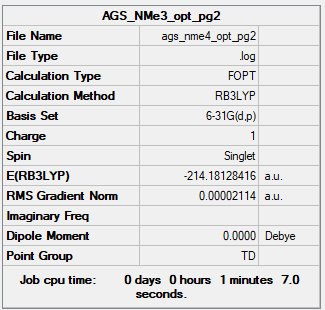
[NMe₄]⁺ Overview

Tetra-methylammonium Ion

B3LYP/6-31G(d,p) level

Frequency Analysis Output File:Media:AGS_NME4_OPT_FREQ.LOG

Optimised [NMe] Molecule

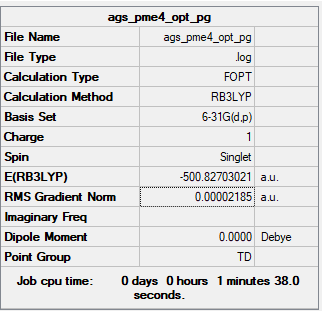
[PMe₄]⁺ Overview

Tetra-methylphosphonium Ion

B3LYP/6-31G(d,p) level

Frequency Analysis Output File:Media:AGS_PME4_OPT_PG_FREQ2.LOG

Optimised [PMe] Molecule

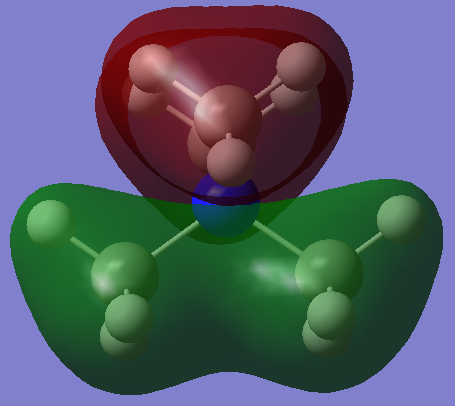
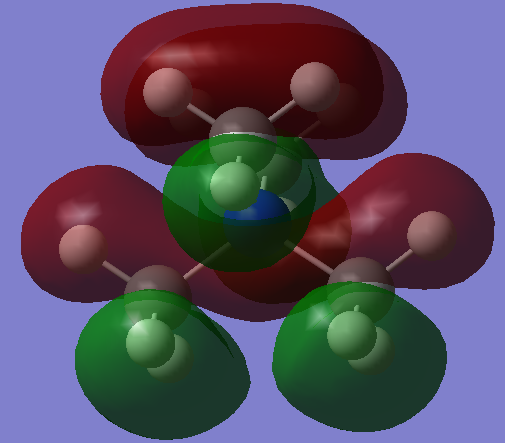
Charge Distribution

Figure 1: Charge Distribution for [NMe₄]⁺ with a scale of of -1.2(dark red) to 1.8(light green) with the charges as N=-0.295 (dark red), C=-0.483 (red) and H=0.269 (green).

Figure 2: Charge Distribution for [PMe₄]⁺ with a scale of of -1.2(dark red) to 1.8(light green) with the charges as P=1.667 (light green), C=-1.060 (red) and H=0.298 (dark green).

Figure 3: Common Representation of [NR₄]⁺] molecules with postive charge placed on Nitrogen

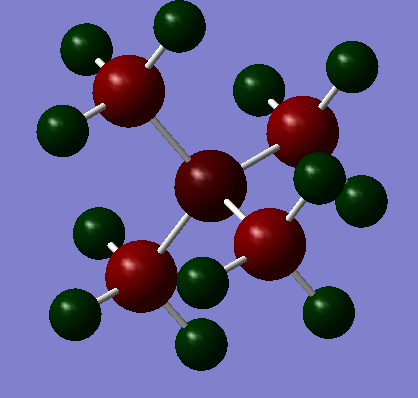
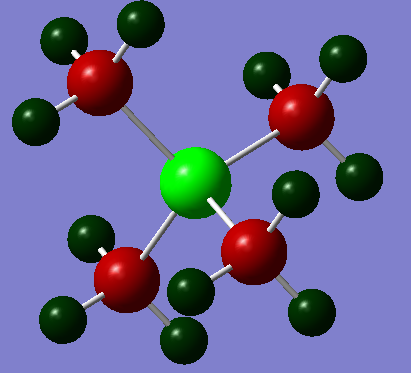
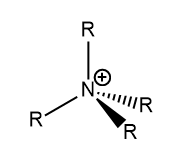
As the above diagrams were both made using the same colour range for charges so you can easily contrast and compare the differing distributions. The standout difference is the vastly different charges for the central nitrogen and phosphorous atoms with the nitrogen having a charge of -0.295 and the Phosphorous having one of +1.667. This can be rationalised by their electronegativities on the Pauling Electronegativity scale: P=2.19, N=3.04, C=2.55 and H=2.20. Of two atoms bonded together, the one with the higher electronegativity will 'pull' the electrons in the bond towards itself resulting in a partially polarised bond; the greater the electronegativity difference then the more polarised the bond.

Therefore the nitrogen will pull electron density away from the carbons because of this and become more negatively charged whereas the phosphorous has a lower electronegativity than carbon so the carbons will pull electron density away from it and make positively charged. This principle of relative electronegativity also explains the different charges on the carbons but not for the hydrogens. Using this principle, you would expect the hydrogens in Figure 1 to have a more positive charge because its bonded to a more positively charged carbon. This shows that this approach is not sufficient to give the whole story and investigating it by MO theory is also needed. To calculate the formal Charge on an atom in molecule you use the following formula:

Formal Charge=Number of Valence Electrons - {Number of electrons in lone pairs - 0.5*(number of bonding electrons)}

For both [NMe₄]⁺ and [PMe₄]⁺ this is:

Formal Charge= 5 - {0 +0.5(8)}= 1

If you compare this with the values for the charges from Guassian in Figure 1 and 2 then you can see this simple formula gives a fairly good approximation for phosphorous but not at all for nitrogen.

The common representation of a [NR₄]⁺] molecule with the positive charge on the nitrogen as seen in Figure 3 is inaccurate by this analysis. The positive charge in fact is distributed between all the hydrogens and the nitrogen is actually negatively charged.

Excellent explanation of where the +1 formal charge arises from in the traditional picture and good comparison between the P and the N charges in particular. The use of referenced electronegativity values to justify the charges is good and your answer could have been improved by considering other effects which do affect the charge distribution (e.g. symmetry). Smf115 (talk) 17:53, 30 May 2019 (BST)

Molecular Orbital Diagrams for [NMe₄]⁺

Fragment Orbitals for Methyl Groups

The Molecular Orbitals for [NMe₄]⁺ were investigated with a focus on all the occupied valence MOs and the 5 lowest energy unoccupied MOs above them.Then MOs number 7, 16 and 21 (the HOMO) were analysed and compared to the LCAO to investigate the bonding, non-bonding or antibonding characteristics of the MOs. To simplify the qualitative approach, the A0s of the methyl fragment were combined to form fragment orbitals (FO) as can be seen above and then these were combined with the AOs of N to give the MOs below.

Molecular Orbital Number 7

This MO is bonding because lots of in phase bond interactions and weaker through space interactions. It has some out of phase interactions, but they are weak and through space so have a smaller impact than the in-phase interactions. There is only one node at the central nitrogen atom so this has a limited impact on the bonding/antibonding character.

Molecular Orbital Number 16

This MO only has contributions from the methyl FOs and not from the Nitrogen which means only four FOs drawn as seen. These FOs are far apart so despite there being some through space bonding and antibonding interactions these have minimal effect, so the MO is non-bonding. Each carbon has a node at its centre, but these again have little impact on the characteristics.

HOMO: Molecular Orbital Number 21

This MO is the Highest Occupied Molecular Orbital-HOMO. It has nodes at each carbon and the nitrogen but also nodes in the region between the nitrogen and the methyl fragments which are antibonding naturally. It also has 3 nodal planes which also are antibonding interactions. On the other side, it has in phase bond interactions too and some weaker through space bonding and antibonding interactions but these have a smaller effect on the bonding/antibonding characteristics. Although difficult to definitively say, I would suggest this a slightly antibonding orbital.

Very nice selection of a range of MOs which have been clearly presented. Good evaluation of the overall character by analysing the interactions and you are largely correct. Only the FO for MO 16 is wrong, notice that one of the H's don't contribute to the FO, considering the BH₃ MO diagram might have helped to assign the FO here. Otherwise, good analysis! Smf115 (talk) 17:58, 30 May 2019 (BST)

Overall, a very good report! Smf115 (talk) 17:58, 30 May 2019 (BST)

<references>