Rep:MOD:AFF8888
NH3 (ammonia)
- Bond Angles = 37.129 degrees
- Bond Lengths = 1.01798 Angstroms
Optimization Calculation:
- Calculation type = OPT + FREQ
- Calculation method = RB3LYP
- Basis set = 6-31G(d.p)
- Final energy = -56.55776873 au
- RMS = 0.00000485
- Point group = C3V
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986258D-10 Optimization completed. -- Stationary point found.
media: NH3_OPTIMISATION_POP_AF1117.LOG
NH3 Vibration:
Animation:
NH3 |
Six vibrational modes are predicted by 3N-6 rule.
These include:
- A pair of degenerate N-H asymmetric stretching modes at 3589.82 cm^-1 (modes 1 and 4).
- A pair of degenerate H-N-H scissoring modes at 1693.95 cm^-1 (modes 2 and 3).
- Symmetric N-H stretching mode at 3461 cm^-1 (mode 4).
- Wagging at 1089 cm^-1 (mode 1). This is also known as the 'umbrella' mode due to its resemblance to the opening and closing motion of an umbrella.
Two bands would be expected for the experimental IR spectrum of gaseous ammonia beacuse the pair of degenerate
NH3 Charge Distribution:
Due to its lone pair and electron-withdrawing ability (high electronegativity), nitrogen is expected to have a slight negative charge. The surrounding hydrogens are expected to have a slight positive charge due to electrons being withdrawn by nitrogen.
This hypothesis is confirmed by gaussview calculation: nitrogen has negative charge of (-0.717) and each hydrogen has slight positive charge of 0.239.
N2
Optimisation Calculation:
- Calculation type = OPT + FREQ
- Calculation method = RB3LYP
- Basis set = 6-31G(d.p)
- Final energy = -109.52412868 au
- RMS = 0.0000006 au
- Point group = D∞h
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401135D-13
Optimization completed.
-- Stationary point found.
N2 Vibration
One vibrational mode of N-N stretching at a frequency of 2457.33 cm^-1.
This vibration is IR inactive since it involves no change in dipole moment.
H2
Optimisation Calculation
- Calculation type = OPT + FREQ
- Calculation method = RB3LYP
- Basis set = 6-31G(d.p)
- Final energy = -1.17853936 au
- RMS = 0.00000017 au
- Point group = D∞h
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
H2 Vibration
One vibrational mode of H-H stretching at frequency of 4465.68 cm^-1.
As with H2, this vibration is IR inactive as there is no change in dipole moment.
Reaction Energy of Harber Process
N2 + 3H2 -> 2NH3
Energies in atomic units, au:
- E(NH3)= -56.55776873
- 2xE(NH3)= -113.11553746
- E(N2)= -109.52412868
- E(H2)= -3.53561808
- 3xE(H2)= -10.60685424
Overall enthalpy change for the Haber process is calculated as follows:
- ΔE=2xE(NH3)-[E(N2)+3xE(H2)]= -0.05579074 au
- Therefore, ΔE=-146.48 kJ/mol
The above calculation shows the product of gaseous ammonia is lower in energy than either of the gaseous reactants, N2 or H2.
Therefore, the ammonia product is more stable than the reactants.
Molecular Orbitals of N2
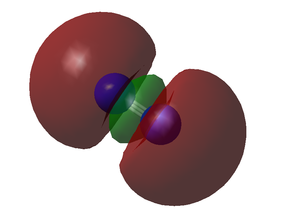
The above image represents the HOMO (highest occupied molecular orbital) of N2. This MO has resulting from end-on overlap of two 2p atomic orbitals, each from a nitrogen atom, to produce a sigma bond. The 2p orbital involved must have correct symmetry, lying along the axis of the bond to allow this end-on overlap.
An additional anti-bonding MO is also generated from the destructive, rather than constructive overlap of these 2p orbitals.
HCl
Optimization Calculation
- Calculation type = OPT + FREQ
- Calculation method = RB3LYP
- Basis set = 6-31G(d.p)
- Final energy = -460.80077847 au
- RMS = 0.00005211 au
- Point group = D∞h
Item Value Threshold Converged?
Maximum Force 0.000090 0.000450 YES
RMS Force 0.000090 0.000300 YES
Maximum Displacement 0.000139 0.001800 YES
RMS Displacement 0.000197 0.001200 YES
Predicted change in Energy=-1.256951D-08
Optimization completed.
-- Stationary point found.
HCl Charge Distribution
Due to its much higher electronegativity compared to hydrogen, it would be expected that chlorine would pull electron density away from hydrogen, resulting in a partial positive dipole on hydrogen and a partial negative dipole on chlorine.
Gauss view shows this to be true: hydrogen has a charge of 0.284 and chlorine has a charge of (-0.284).
HCL Vibration
HCl has one vibrational frequency at 2956.80 cm^-1. This is as predicted by the rule 3N-5 for a linear molecule.
HCl molecular orbitals
Chlorine has 17 electrons, giving it the configuration: 1s2, 2s2, 2p6, 3s2, 3p6. Hydrogen has one electron, residing in its 1s orbital.
Chlorine has a higher electronegativity than hydrogen and therefore more tightly holds onto its electrons. This high electronegativity stabilizes chlorine's electrons which therefore reside in atomic orbitals which are far deeper in energy than that of hydrogen's one electron. As a result, the atomic orbitals of up to 3s in chlorine are too low in energy to overlap with the hydrogen 1s atomic orbital. Only the 3p atomic orbital of chlorine is screened/distanced enough from the attractive nucleus to be sufficiently high in energy for overlap with the hydrogen 1s to produce an s-p hybrid molecular orbitals.
Only a 3p-orbital of chlorine with the correct symmetry, i.e the one lying along the axis of the bond which able to overlap end-on with the hydrogen 1s orbital, generating a 'sigma bond'. The other two 3p orbitals of chlorine are non-bonding molecular orbitals.
The overlap described above results in s-p hybrid two molecular orbitals:
- The bonding MO, resulting from a 'positive combination' of the atomic orbitals. Here, the orientation of the atomic orbitals is such that the positive phase of the 3p is has a greater region of overlap with the positively phased 1s compared to the negative phase of the 3p. Consequently, there is a greater region of constructive interference in the resulting molecular orbital, having a stabilizing effect.
- The anti bonding MO, resulting from a 'negative combination' of the atomic orbitals where the negative phase of the 3p has a greater overlap with the 1s than the positive phase of the 3p, setting up a greater region of destructive interference in the resulting molecular orbital. The area of destructive interference, where the positive and negative wave functions of the respective atomic orbitals have 'cancelled' each other out is an area of zero electron density known as a 'nodal plane'. This has a destabilising effect on the anti bonding orbital which is consequently higher in energy than the bonding MO.
Molecular orbitals are filled in accordance with the Aufbau Principle (from lowest to highest energy), so the bonding orbital is filled before the anti bonding. The vacant anti bonding orbital is thus referred to as the 'lowest unoccupied molecular orbital' or the 'LUMO'. In contrast, the bonding orbital, just below, is known as the 'HOMO', the 'highest occupied bonding orbital'.
Below are representations of the molecular orbitals of HCl, generated by gauss view calculations, from highest to lowest energy:

- This is the LUMO, resulting from, as described above, linear combination of the the 1s hydrogen atomic orbital with a 3p atomic orbital of chlorine.
- The 3p atomic orbital of chlorine involved must lie across the axis of the bond to allow the end-on overlap with the hydrogen 1s. Therefore, the 3p orbital involved is the 3px or the 3py.
- The combination is such that opposite phases of the atomic orbitals have greatest overlap, resulting in a greater region of destructive interference, where the wave functions of each atomic orbital cancel each other out, giving a nodal plane of zero electron density which is clearly visible above.
- The above LUMO is assigned the notation 'u' for 'ungerada', to describe the fact that going from one side of its center of inversion to the other results in a change in the sign of the wave function.

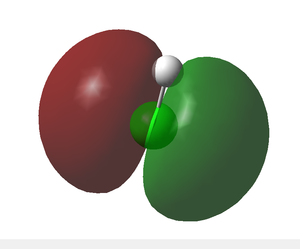
- Above are the two degenerate HOMOs, each of which contains two electrons.
- These are in fact 'non-bonding' molecular orbitals since they originate only from the chlorine, i.e. are not generated by atomic orbital overlap of hydorgen and chlrone.
- These are the two 3p orbitals of chlorine with incorrect symmetry for overlap with the hydrogen 1s.
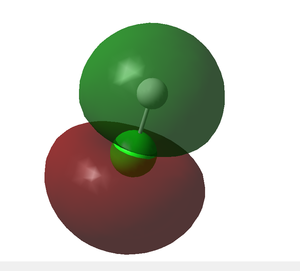
- Above is the bonding molecular orbital corresponding with the hydrogen 1s overlapping with the chlorine 3p of correct symmetry described earlier.
- The greater s-character of the resulting s-p hybrid has a stabilizing effect as electrons are held more tightly; hence, the s-p hybrid is lower in energy than the above 3p MOs which have a full p-character.
- It is observed that electron density mostly resides on the chlorine atom (shown in green). This is due to chlorine's higher electronegativity drawing electrons of the sigma bond towards itself.
- This representation is verified by the charge distribution analysis of HCl which suggests a partial negative dipole on the chlorine atom as a result of the higher electron density surrounding it.
- The HOMO is assigned 'g' for 'gerada', indicating that traversing through the center of inversion will cause no change in the sign of the wave function.
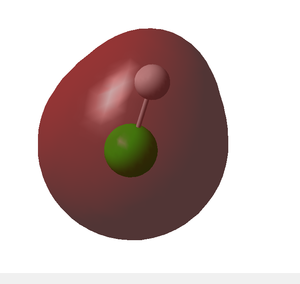
- This represents the MO resulting from the chlorine 3s atomic orbital.
- Being too high in energy for overlap with the hydrogen 1s, this MO is non-bonding.
- Electron density is clearly concentrated around the chlorine atom due to its higher electronegativity.
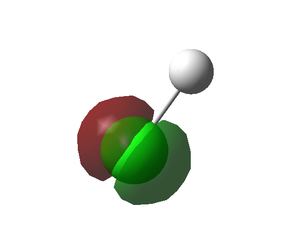


- The above three MOs correspond to the three degenerate 2p orbitals of chlorine, each of which lies across an axis: x, y or z.
- These orbitals, being subject too the high electronegativity of chlorine, are too deep in energy to interact with hydrogen's 1s, hence, they are non-bonding MOs.
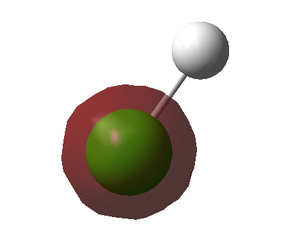
- This MO corresponds to the 2s chlorine.
- As previously, the 2s atomic orbital of chlorine is not comparable in energy with the hydrogen 1s, preventing any interaction. Therefore, these electrons are non-bonding.

- The lowest energy MO originates from the chlorine 1s atomic orbital.
- Comparison to the above MO shows the region electron density has contracted and now encompasses only the area defined by the chlorine nucleus.
- This would also be evident in the radial distribution function for this 1s MO orbital which would show electron density residing very close to the chlorine nucleus.
Overall, HCl has 2 bonding electrons and 0 anti bonding electrons, giving it a bond order of 1.
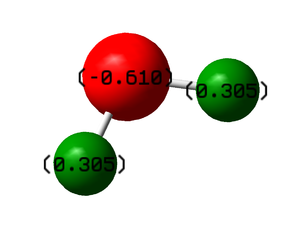
Charge Distribution Analysis of H2O
H20 is highly polar due to the high electronegativity difference of its constitute atoms, hydrogen and oxygen.
Oxygen has a much higher electronegativity than hydrogen which have 3.3 and 2.2 electronegativity on the Pauling scale respectively.
This results in a strongly negative dipole resulting from high electron density on the oxygen atom and positive dipoles on each hydrogen due to electron deficit.
As a consequence, strong inter-molecular interactions between oppositely charged dipoles on the water molecules occur, known as hydrogen bonding.
Below is the charge analysis of water, clearly showing the positive and negative charges on the hydrogen's and oxygen respectively.