Rep:MOD:ACHUNTUN
The Cope Rearrangement
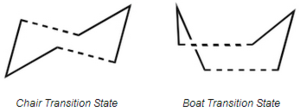
The Cope Rearrangement is an organic reaction which incorporates a [3,3]-sigmatropic shift of a 1,5-diene molecule. An example is seen above. In this report the reaction mechanism is determined for the Cope Rearrangement of 1,5-hexadiene by finding the low-energy minima and transition states of the molecule. The transition states[1] are shown below. It is widely known that the reaction is of a concerted nature. The reaction goes through a higher energy "boat" transition structure and a lower energy "chair transition structure.
Optimising Reactants and Products
Anti Conformer
A molecule of 1,5-hexadiene with "anti" linkage was drawn in GaussView. It was optimised using the HF/3-21G method. The calculation was then run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the anti conformer can be viewed here.
Point Group: C2
Energy: -231.69260237 a.u.
Gauche Conformer
A molecule of 1,5-hexadiene with "gauche" linkage was drawn in GaussView. It was optimised using the HF/3-21G method. The calculation was then run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the anti conformer can be viewed here.
Point Group: C1
Energy: -231.69266122 a.u.
Lowest Energy of Conformations
The anti molecule is expected to have a lower energy than the gauche conformer. This is because of stereoelectronics. If there is a complete antiperiplanar relationship between the central carbon atoms, this will lead to the lowest energy possible. However it is also possible that there are gauche conformations with a lower energy. This is because there may be more some sigma donation into the pi orbitals of the alkene groups on either end of the hexadiene. There may also be some van der waals forces in some gauche conformations leading to a lower energy.
After drawing other conformations on Gaussview, it was found that the above drawn gauche conformer is the lowest energy conformer followed by the already drawn anti conformer. This is because sigma/pi donation is at a maximum in the alkene group with van der waals interactions between the hydrogens also at a maximum. Pauli repulsion between the filled sigma C-H orbitals was curtailed in this conformation of the molecule which explains why its energy is so low.
The gauche conformation drawn previously is the gauche3 conformation while the anti conformation is the anti1 conformation.
Anti Conformation (Ci symmetry)
Optimisation by HF/3-21G method
The Ci anti2 conformation was found and optimised at the HF/3-21G level of theory. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Point Group: Ci
Energy: -231.69253525 a.u.
Its symmetry and energy are the same as the Ci anti2 conformation found in Appendix 1.
Optimisation by B3LYP/6-31G* (DFT) method
The Ci anti2 conformation was optimised at the B3LYP/6-31G* (DFT) level of theory. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Point Group: Ci
Energy: -234.61170287 a.u.
The symmetry has remained the same as for the HF/3-21G method. However the energy is more negative than the energy calculated for the HF/3-21G method. The geometry does not change especially with the symmetry staying the same.
Frequency Analysis
A frequency analysis was undertaken on the optimised Ci molecule. It was confirmed that the critical point was a minimum on the PES by ensuring that the vibrational frequencies are real and positive values.
Low frequencies --- -18.4366 -11.7094 -0.0011 -0.0011 -0.0004 1.9411 Low frequencies --- 72.7501 80.1522 120.0362
Below are the thermochemistry energies:
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821
Optimising the "Chair" and "Boat" Transition Structures
Chair Conformation
The transition states of the Cope Rearrangement were optimised by the Hartree Fock with 3-21G basis set method and a method where the reaction coordinates were freezed. It is difficult to know the negative direction of the curvature of the PES which makes it difficult to optimise a transition state. If the transition state is incorrectly predicted the reaction could proceed in the wrong direction and form reactant molecules. If the geometry of the transition state is predicted to a moderate level of preciseness, the force constant can be calculated in the optimisation easily. However if the transition state is inaccurate then teh curvature of the the PES can be different at various points which are not close to the transition state. Therefore it is better to freeze the reaction coordinate of the transition state and then minimising the rest of the molecule and then unfreezing the reaction coordinate followed by optimising the transition state.
Hartree=Fock
An allyl fragment (CH2CHCH2) was optimised using the Hartree-Fock with 3-21G basis set method. Two of the fragments were oriented on top of one another with 2.2Å between the terminal ends of the ally fragments. This is known as the guessed chair transition state. This was then optimised using the Hartree-Fock with 3-21G basis set method with force constants and optimised to a Berny transition state. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here
The lowest vibration found was the imaginary frequency 817.72 cm-1 which shows the frequency calculation was completed. The bond vibration is proof of the Cope Rearrangement where a bond is formed and broken at either end of the allyl fragment. The distance between the terminal C atoms that are to form new C-C bonds is 2.02 Å.
Energy: -231.61932243 a.u.
Frozen Coordinate Method
The guessed chair transition state was optimised using the frozen coordinate method. The 2 C-C bonds that are formed/broken were frozen so their distances were 2.2Å . The rest of the molecule was optimised to a minimum with a QST2 method.
The output molecule resembled the molecule from the Hartree-Fock method in geometry but the 2 C-C bonds to be formed were 2.2Å apart. The bonds were unfrozen and this was then optimised using HF/3-21G to a Berny transition state method.
The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
The resulting transition state has the same geometry as the output molecule from the Hartree-Fock method. The formed C-C bonds again have a length of 2.02. This shows that the same molecule can be obtained using both methods.
Energy: -231.61932091 a.u.
Boat Conformation
The boat transition structure was optimised using the QST2 method. The calculation failed the first time because the guessed transition state was too different to the real transition state. To resolve this, the dihedral angle of the central four carbon atoms was set to 0 degrees and each inside C-C-C bond angle to 100 degrees for both reactant and product structures. The QST2 method was then run again.
The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Energy: -231.60280248 a.u.
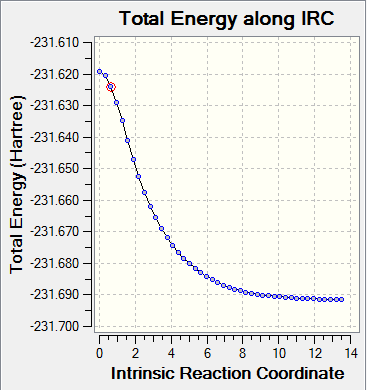
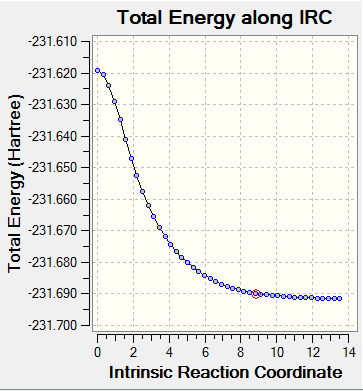
Intrinsic Reaction Coordinate(IRC)
The IRC is the minimum energy path from a a transition structure down to its local minimum on a potential energy surface. Using the IRC method it is possible to identify the resultant conformer from a specific transition state. This can be found by taking small steps towards the part of the energy surface where the gradient is steepest.
The direction of the IRC path was chosen as forwards as the reaction is symmetrical. The optimised chair transition state was used to run the forward reaction. Force constants were always calculated and the number of points calculated was set to 50.
The results from the calculation was published onto D-Space.
Energy: -231.69157869 a.u.
The IRC did not reach a minimum geometry. The calculation was rerun with the 100 points being computed along the IRC.
Energy: -231.68950555 a.u.
Activation Energy
The activation energies of the transitions structures can be calculated reoptimising the structures at the B3LYP/6-31G* (DFT) level and then by carrying out a frequency calculation. The HF/3-21G optimised structures were used to complete the calculations.
Optimising Chair TS
For the chair TS HF/3-21G TS Berny structure was used for further optimisation.
The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Energy: -234.55698536 a.u.
The energy was slightly higher than for the previous method.
Frequency Analysis of Chair TS
The frequency analysis was carried out using the B3LYP/6-31G* basis set method.The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Energy: -234.55698536 a.u.
The energy is the same as that for the optimisation showing that the calculation ran correctly.
Sum of electronic and zero-point Energies= -234.414924 Sum of electronic and thermal Energies= -234.409005 Sum of electronic and thermal Enthalpies= -234.408061 Sum of electronic and thermal Free Energies= -234.443808
Optimising Boat TS
The optimisation of the boat structure was run with the B3LYP/6-31G basis set method to find the transition state. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here..
Energy: -234.54309304 a.u.
Frequency Analysis of Boat TS
The frequency analysis was done using the same method as that for the chair TS. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Energy: -234.54309304 a.u.
The energy is the same as that for the optimisation showing that the calculation ran correctly.
Sum of electronic and zero-point Energies= -234.402339 Sum of electronic and thermal Energies= -234.396005 Sum of electronic and thermal Enthalpies= -234.395061 Sum of electronic and thermal Free Energies= -234.431748
| HF/3-21G (hartrees) | B3LYP/6-31G(d) (hartrees) | Activation Energy, ΔE (kcal/mol) | |
|---|---|---|---|
| Chair TS | -231.61932243 | -234.55698536 | 34.33572998259 |
| Boat TS | -231.60280248 | -234.54309304 | 43.05328581347 |
| Anti2 (reactant) | -231.69253525 | -234.61170287 |
When the transition states are optimised further, the geometry of the transition does not change very much but there is a large difference in energy. The energies calculated correspond well to the experimental data in the lab script as they are within the error stated. The reaction is likely to occur through the chair transition state. This is because this state is less hindered [1]. There will be some error in calculating the activation energy. This is because we are using the anti 2 conformer for calculation when the IRC state that the react/product going via the chair transition state is the gauche 2 conformer. This will have a higher energy than the anti 2 conformer.
Diels Alder Cycloaddition
The Diels Alder reaction is a concerted pericyclic reaction and occurs via a single transition state. It is a cycloaddition reaction between a conjugated diene and an alkene where two pi bonds are broken and two sigma bonds are formed. One way the reaction can occur is if there are 6 electrons (4n+2) in the system and symmetry is maintained.
Diels Alder Reaction: Butadiene and Ethene
Optimising Butadiene
Cis-butadiene was optimised using the semi-empirical molecular orbital AM1 method. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
The symmetry of the molecule is C2v.
| HOMO ( Orbital 11) | LUMO ( Orbital 12) |
|---|---|
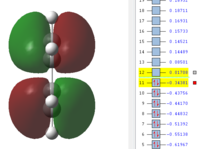 |

|
| Anti-symmetric | Symmetric |
Finding Transition State
An envelope structure was created whereby the overlap between the ethene pi orbitals and butadiene pi orbitals were at a maximum. The distance between the C atoms which formed new sigma bonds in the Diels Alder was 2.2Å. First the frozen coordinate method was used with the semi-empiricial with AM1 basis set method. This followed by running an optimisation and frequency calculation to a Berny transition state. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Energy: -0.11165524 a.u.
Low frequencies --- -955.9398 -4.7579 -4.2947 -0.0031 0.0057 0.0310 Low frequencies --- 5.7209 147.0102 246.6425
There is one imaginary vibrational mode at -955.9398cm-1. This correspons to the formation of the the C-C bonds on the terminal carbons of butadiene and ethene.
The ethene molecule goes towards the face of the butadiene from either above or below the plane of the molecule. This is so orbitals of the appropriate symmetry can interact leading to sigma bonds forming between the terminal ends of the butadiene and ethene.
The bond length of the incompletely formed sigma bonds in the transition state were 2.11922Å. Below are the bond lengths of C-C of different hybridisation.
C-C sp3-sp3: 1.53 Å C-C sp2-sp2: 1.46 Å [2]
The Van der Waals radius of carbon is 1.70Å[3].
The partly formed C-C bond in the transition state is less than twice the van der waals radius of a carbon atom. Therefore the orbitals of the atom are able to interact which is an indicator of bonding character. We know the bond has not completely formed because its bond length is so much longer than a standard C-C bond which shows that we have a transition structure.
Reaction Pathway
The above vibration is the imaginary frequency at -955.94 cm-1 corresponding to the reaction pathway at the transition state is shown above. Two sigma bonds are forming between the terminal carbons of the butadiene and ethene. The bond formation is synchronous.
The above vibration is the lowest positive vibration at 147.01cm-1. This is different to the imaginary frequency because it involves the motion of the constituents separately and is not synchronous. There are low energy vibrations into and out of the plane of the molecule and no interaction between the two molecules.
HOMO and LUMO
| HOMO (17) | LUMO (18) |
|---|---|
 |

|
The HOMO at the transition structure is anti-symmetric. This is expected because the product of the reaction is also anti-symmetric. The HOMO of the butadiene and the LUMO of the ethene molecule form the MOs which form the product. This yields an anti-symmetric transition state. The orbital symmetry stays the same in the reaction. The HOMO of the butadiene and the LUMO of the ethene molecule react to form two sigma bonds. These two thigns paired together enables the reaction to happen.
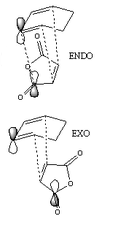
Regioselecivity in the Diels-Alder Reaction
The Exo and Endo transition states were calculated using the Frozen Coordinate Method. the forming bonds were frozen 2.2Å apart. The optimisation on the frozen structure was run with the semi-empirical AM1 method and optimised to a minimum.
To complete the calculation and find the transition state the frozen bonds were unfrozen . the OPT+FREQ method with the AM1 method was run to a TS(Berny) with the force constants calculated once and the key words NoEigen.
Calculation of the Exo Transition State
The exo transition state was calculated by first guessing a structure for the molecules. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Low frequencies --- -811.7719 -0.4502 -0.2678 -0.0047 1.7520 3.1066 Low frequencies --- 3.9508 60.9830 123.8820
There is one imaginary vibrational mode at -811.7719cm-1. This corresponds to the formation of the the C-C bonds on the terminal carbons of the two components.
Energy: -0.05041993 a.u.
| HOMO (34) | LUMO (35) |
|---|---|
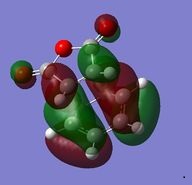 |
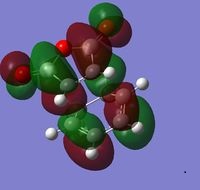
|
Calculation of the Endo Transition State
The endo transition state was calculated by first guessing a structure for the molecules. The results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Low frequencies --- -806.4601 -1.6492 -1.4434 -0.6727 -0.0104 0.4888 Low frequencies --- 0.9280 62.4415 111.7368
There is one imaginary vibrational mode at -806.4601cm-1. This corresponds to the formation of the the C-C bonds on the terminal carbons of the two components.
Energy: -0.05150480 a.u.
| HOMO (34) | LUMO (35) |
|---|---|
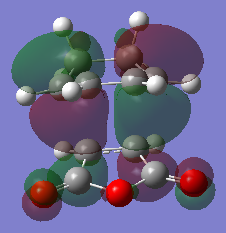 |
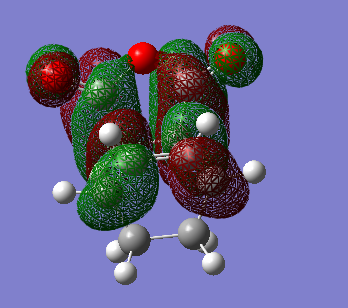
|
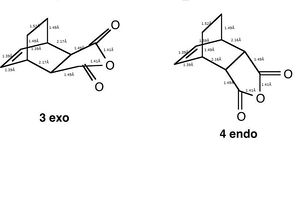
Comparing Structures
The above diagram shows the various bond lengths of the two structures.
The preferred structure of the reaction is affected by steric repulsion and the strain of the system against the possible secondary orbital interactions. These secondary orbital interactions occur between the pi system in the double bond on the formerly cyclohexa-1,3-diene and the pi system of the -(C=O)-O-(C=O)- of the former maleic anhydride. In the exo product there is steric hindrance from the oxygen on the maleic anhydride and the carbons of the -CH2-CH2- bridge. The bond lengths in the two molecules are very similar. However the energies of the two structures is different. The endo structure is 0.0068 a.u. lower in energy than the exo structure. Seeing as the endo transition state is lower in energy, it means that the endo product is the kinetic product of the reaction.
Both structures have a node present between the HOMO of cyclohexa-1,3-diene and the LUMO of the dienophilie which in turn gives an antisymmetric orbital.The secondary orbital effect also gives preference to the endo structure.
In the endo structure there is overlap between an orbital on carbon of the -CH=CH- fragment and an orbital on the carbon of the C=O bond in maleic anhydride. This howeveer is not the case for the exo structure. This bonding type overlap gives the transition state added stability. This is another reason for the endo structure being the kinetic prduct for the reaction.
References
<references>
<ref name="hindered"> DOI:10.1021/ja00221a092 <ref name="C Bond Lengths" > F.H. Allen, O. Kennard, D.G. Watson, et.al., Tables of Bond Lengths determined by X-Ray and Neutron Diffraction. Part 1. Bond Lengths in Organic Compounds., J. Chem. Soc. Perkin Trans. 2., 1987, S1-S19., DOI:10.1039/P298700000S1
<ref name="C VdW Radii" > A. Bondi., Van der Waals Volumes and Radii., J. Phys. Chem., 1964, 68 (3) pp 441-451., DOI:10.1021/j100785a001