Rep:MOD:3ggs
EX3 Section
BH3
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
BH3 Optimisation File Name = CH_BH3_OPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 3-21G Charge = 0 Spin = Singlet E(RB3LYP) = -26.46226429 a.u. RMS Gradient Norm = 0.00008851 a.u. Imaginary Freq = Dipole Moment = 0.0003 Debye Point Group = CS Job cpu time: 0 days 0 hours 1 minutes 53.0 seconds.Result text document |
Item Value Threshold Converged? Maximum Force 0.000220 0.000450 YES RMS Force 0.000106 0.000300 YES Maximum Displacement 0.000709 0.001800 YES RMS Displacement 0.000447 0.001200 YESLog File |
|
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
BH3 Optimisation File Name = CH_BH3_OPT_6-31Gdp File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -26.61532360 a.u. RMS Gradient Norm = 0.00000707 a.u. Imaginary Freq = Dipole Moment = 0.0001 Debye Point Group = CS Job cpu time:0 days 0 hours 0 minutes 32.0 seconds.Result text document |
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000061 0.001800 YES
RMS Displacement 0.000038 0.001200 YES
Predicted change in Energy=-1.069388D-09
Optimization completed.
-- Stationary point found. Log file |
|
| Bond Lengths (Ao) | Bond Angles (o) |
|---|---|
| 1.19231 | 120.001 |
| 1.19231 | 119.994 |
| 1.19232 | 120.005 |
GaBr3
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
GaBr3 optimisation using pseudopotentials File Name = CH_AsBr3_pp_opt1.log File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -41.70082770 a.u. RMS Gradient Norm = 0.00000016 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 15.0 seconds.Result text document |
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000003 0.001800 YES
RMS Displacement 0.000002 0.001200 YES
Predicted change in Energy=-1.307743D-12
Optimization completed.
-- Stationary point found.
DOI:10042/31151 |
|
| Bond Lengths (Ao) | Bond Angles (o) |
|---|---|
| 2.35018 | 120.000 |
| 2.35018 | 120.000 |
| 2.35018 | 120.000 |
BBr3
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
BBr3 Optimisation NEW File Name = FIN_BBr3_OPTNEW_CH File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -64.43644971 a.u. RMS Gradient Norm = 0.00000977 a.u. Imaginary Freq = Dipole Moment = 0.0004 Debye Point Group = CS Job cpu time:0 days 0 hours 0 minutes 34.9 seconds.Results text document |
Item Value Threshold Converged?
Maximum Force 0.000016 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000075 0.001800 YES
RMS Displacement 0.000044 0.001200 YES
Predicted change in Energy=-1.642101D-09
Optimization completed.
-- Stationary point found.
DOI:10042/31194 |
|
| Bond Lengths (Ao) | Bond Angles (o) |
|---|---|
| 1.93395 | 119.997 |
| 1.93394 | 120.001 |
| 1.93401 | 120.002 |
Compare and Contrast
What is a bond?
A chemical bond is primarily an electrostatic force of attraction between two oppositely charged molecules such as a nucleus and electron.There are many forms they can come in including; Covalent, Ionic, Metallic, Hydrogen, Dispersion Interactions (such as London Dispersion's) and Dipole-Dipole interactions. The bond length exists at equilibrium in a potential minima, where there is a balance between attractive and repulsive forces as shown by a Lenard-Jones potential to a basic level.
| Bond Type | Ionic | Covalent | London Dispersion | Hydrogen | Dipole-Dipole |
|---|---|---|---|---|---|
| Bond Energy (Kcalmol-1) | 4000-250 | 260-30 | <15-1 | 12-1 | 2-0.5 |
- ↑ Clayden , Greaves , Warren Inorganic Chemistry 2nd Edition
As shown in the table the relative energies of some of these interactions are shown from strongest to weakest. Gaussian does not always shown bonds as it is programmed to recognize those that exist at the energy minima (IE literature results) since an coulombic interaction can actually take space over a greater distance it is possible to have larger bonds where the molecule is in an excited state, in order for the bond to dissipate the fully the bond length must tend to infinity.
Bond length comparisons
| Molecule | Bond Lengths (Ao) | Bond Angles (o) |
|---|---|---|
| BH3 | 1.19231 | 120.001 |
| GaBr3 | 2.35018 | 120.000 |
| BBr3 | 1.93395 | 120.000 |
H and Br are similar in that they each have one unpaired electron outside of that no real similarities exist. Differences are primarily the size of the atoms , Br being much larger and also the electronegativity , Br being more electronegative. These factors effect both overlap of the orbitals , more electronegative being held closer to the atom additionally steric factors may occurs from sizes of atoms. B and Ga are similar as they are in the same group, however Ga is in a lower period so is larger due to higher occupancy also orbitals such as the d orbital are occupied whereas B is s and p. All molecules the bond are sp2 hybridized so this is not a factor effecting bond length difference.
As shown in the data bond length increases going from BH3 to BBr3 . The pure length suggest the B-Br bond is weaker , this is likely due to the fact Br is much lower in the periodic table hence its outer occupied orbitals are 3p a larger more diffuse orbital comparable to the 1p on boron this creates an energy mismatch and hence weaker overlap. boron is much closer to H in the table as 1s is closer to 1p leading to a stronger overlap. Lower down the group the more electron shells hence the nucleus is ore shielded from charge and attraction between other electron clouds and it will hence be weaker.
Similarly to this going from BBr3 to GaBr3 bond length again increases Ga is much lower in the periodic table than boron hence has larger diffuse 3p orbitals , these match better with 3p on Br however the weak permeation leads to a weak bond which is a lot longer. Bond length gives an approximation for strength however this is not always correct due to other effects such as lone pair repulsion. The absolute strength can be determined from IR as in the next section the Harmonic oscillator approach where the force is proportional to a force constant 'k' gives an indication of bond strength, larger k meaning a stronger bond. Where E=0.5kx2 for IR transitions and x is the displacement.
All bond angles are 120 degrees so a good amount of precision this is expected as all compounds are sp2 hybridised and trigonal planar.
BH3 Predicted IR Frequencies
Summary
BH3 Frequency File Name = CH_BH3_OPT_6-31GDP_Frequency1 File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -26.61532363 a.u. RMS Gradient Norm = 0.00000291 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 31.0 seconds. Low Frequencies Low frequencies --- -0.9432 -0.8611 -0.0055 5.7455 11.7246 11.7625 Low frequencies --- 1162.9963 1213.1826 1213.1853
CH_BH3_OPT_6-31GDP_FREQUENCY1.LOG
| Frequency (cm-1) | Intensity | IR Active y/n | Type |
|---|---|---|---|
| 1163 | 93 | y | bend |
| 1213 | 14 | y | bend |
| 1213 | 14 | y | bend |
| 2582 | 0 | n | stretch |
| 2715 | 126 | y | stretch |
| 2715 | 126 | y | stretch |
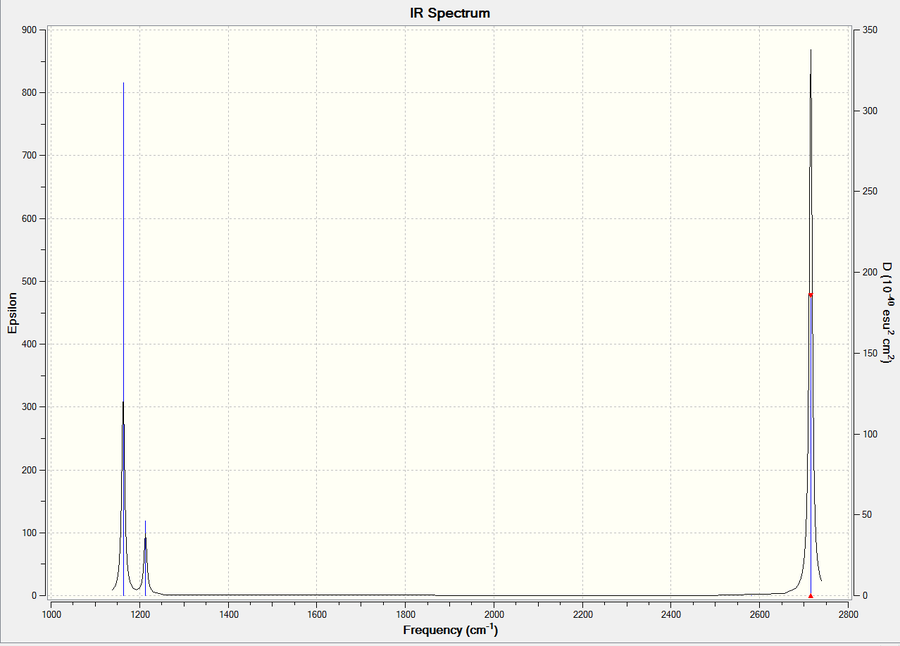
In the above spectrum only 3 peaks are visible this can be seen from the table , two sets are at a almost identical peak hence are degenerate modes, these overlap. One mod as stated in the table is IR inactive so doesn't appear this leaves the 6-3 = 3 visible peaks shown.
GaBr3 Predicted IR Frequencies
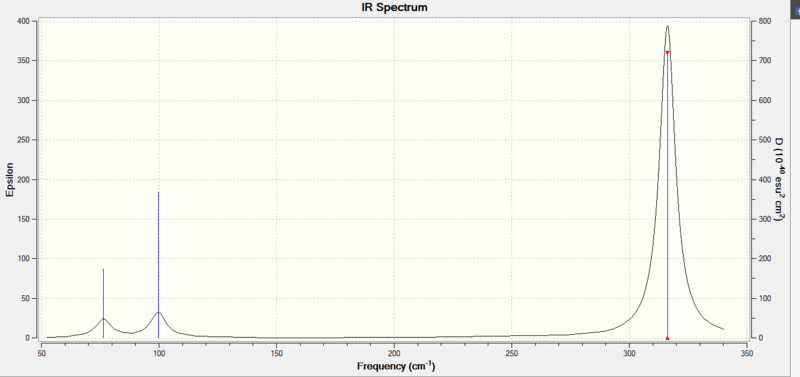
Low frequencies --- -0.5219 -0.5214 -0.0024 -0.0010 0.0236 1.2010 Low frequencies --- 76.3744 76.3753 99.6982 summary GaBr3 freq analysis File Name = CH_GaBr3_OUTput_freq File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -41.70082783 a.u. RMS Gradient Norm = 0.00000069 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = C3H Job cpu time: 0 days 0 hours 0 minutes 10.4 seconds.
| Frequency cm^-1 | Intensity | Active | Mode |
|---|---|---|---|
| 76 | 3 | y | Bend |
| 76 | 3 | y | Bend |
| 99 | 9 | y | Bend |
| 197 | 0 | n | Stretch |
| 316 | 57 | y | Stretch |
| 316 | 57 | y | Stretch |
IR comparison
| Frequency (cm-1) | Intensity | IR Active y/n | Type |
|---|---|---|---|
| 1163 | 93 | y | bend |
| 1213 | 14 | y | bend |
| 1213 | 14 | y | bend |
| 2582 | 0 | n | stretch |
| 2715 | 126 | y | stretch |
| 2715 | 126 | y | stretch |
It is apparent the frequencies of vibrations are higher for both stretches and bends of BH3 as previously predicted this is in accordance with the prediction BH3 has stronger bonds. Higher frequency means a higher energy vibrational transition hence greater force constant k meaning the BH3 bond is significantly stronger. Both molecules have the same number of vibrational modes since both have the same number of atoms and point group (D3h).
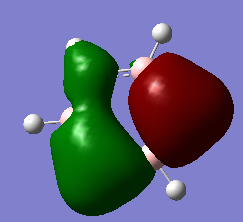
BH3 Molecular Orbitals
[Molecular Orbital Diagram used from]
Calculation log: DOI:10042/31246
Are there any significant differences between the real and LCAO MOs?
The energy deviation shown for the non-bonding orbital was -0.09 this shows a deviation from the ideality as a non bonding orbital should reside at 0 since it is neither stabilized or destabilized hence a deviation is shown. Additionally the orbitals appear larger so in 2e/ some constructive overlap is shown. A final deviation is due to the symmetry of the molecule not being forced, this has lead to e/ orbitals being non-symmetric due to a slightly non-symmetric geometry.
What does this say about the accuracy and usefulness of qualitative MO theory?
Outside of that it shows a good agreement in the energetical placement and shape/ appearance of the orbitals. Since the similarities allowed the mo's to be assigned it is clearly a good agreement.
NH3 Optimization and Molecular Orbitals
Optimization
Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000018 0.001800 YES RMS Displacement 0.000011 0.001200 YES Predicted change in Energy=-2.907265D-10 Optimization completed. -- Stationary point found.
Title Card Required File Name = nh3 OPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -56.55776856 a.u. RMS Gradient Norm = 0.00000587 a.u. Imaginary Freq = Dipole Moment = 1.8465 Debye Point Group = C3V Job cpu time: 0 days 0 hours 0 minutes 14.0 seconds.
Optimized NH3 |
Frequency Analysis
Summary
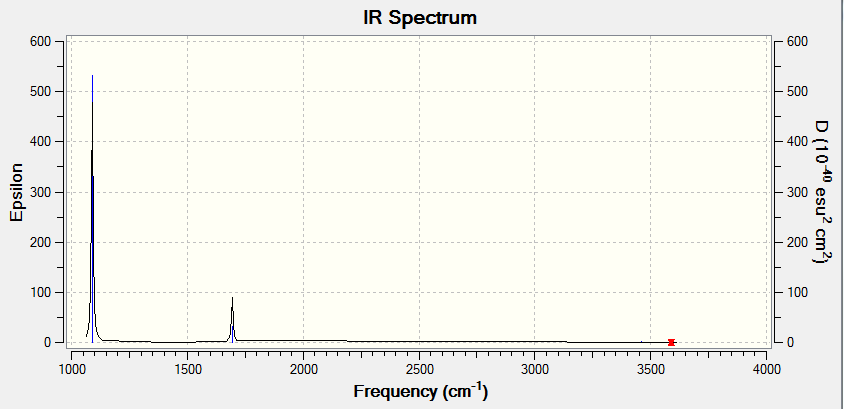
Title Card Required File Name = nh3_freq_input File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -56.55776856 a.u. RMS Gradient Norm = 0.00000587 a.u. Imaginary Freq = 0 Dipole Moment = 1.8465 Debye Point Group = C3 Job cpu time:0 days 0 hours 0 minutes 18.0 seconds.
Frequency data
Low frequencies --- -8.5647 -8.5591 -0.0044 0.0454 0.1785 26.4185
Low frequencies --- 1089.7602 1694.1865 1694.1865
Frequencies -- 1089.7602 1694.1865 1694.1865
Red. masses -- 1.1800 1.0644 1.0644
| Frequency | Intensity | Active (y/n) | Type |
|---|---|---|---|
| 1089 | 145 | y | Bend |
| 1694 | 14 | slightly | Bend |
| 1694 | 14 | slightly | Bend |
| 3461 | 1 | n | Stretch |
| 3589 | 0 | n | Stretch |
| 3589 | 0 | n | Stretch |
NH3 Population Analysis
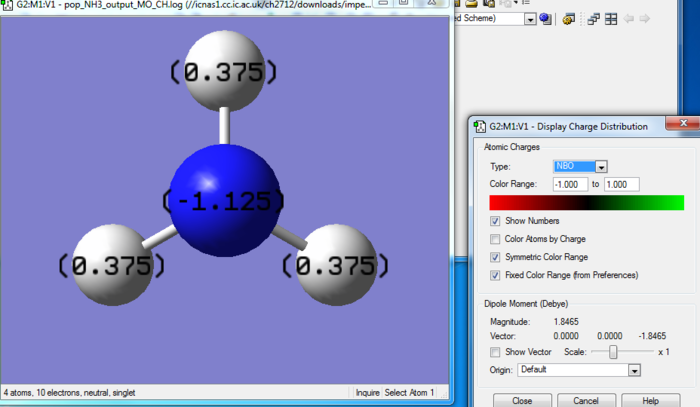
NH3 NBO Analysis
Charge range: -1.00 to 1.00 .
As expected H is electropositive and N electronegative , which is in agreement with theory also as N has higher electron count.
NH3BH3 Section
Item Value Threshold Converged?
Maximum Force 0.000123 0.000450 YES
RMS Force 0.000058 0.000300 YES
Maximum Displacement 0.000515 0.001800 YES
RMS Displacement 0.000296 0.001200 YES
Predicted change in Energy=-1.635911D-07
Optimization completed.
-- Stationary point found.
BH3NH3 Optimization
File Name = BH3NH3_OPT_input
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Charge = 0
Spin = Singlet
E(RB3LYP) = -83.22468893 a.u.
RMS Gradient Norm = 0.00005974 a.u.
Imaginary Freq =
Dipole Moment = 5.5651 Debye
Point Group = C1
Job cpu time:0 days 0 hours 2 minutes 20.0 seconds.
Optimized BH3NH3 |
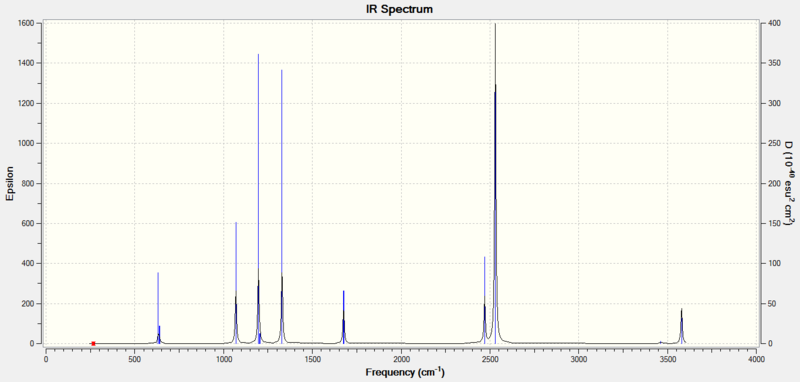
BH3NH3 IR data
Low frequencies --- -16.6222 0.0009 0.0015 0.0017 29.7206 44.7226 Low frequencies --- 267.5555 632.0750 638.0630
| Wavenumber cm^-1 | Intensity | Active | Type |
|---|---|---|---|
| 268 | 0 | no | Twist |
| 632 | 14 | slight | stretch |
| 638 | 4 | no | Rocking |
| 641 | 4 | no | Twist |
| 1069 | 40 | yes | Rocking |
| 1070 | 40 | yes | Rocking |
| 1196 | 108 | yes | Wagging |
| 1204 | 4 | no | Scissoring |
| 1204 | 4 | no | Scissoring |
| 1329 | 114 | yes | wagging |
| 1676 | 28 | yes | Scissoring |
| 1676 | 28 | yes | Scissoring |
| 2470 | 67 | yes | symmetric str. |
| 2530 | 231 | yes | anti-symmetric str. |
| 2530 | 231 | yes | anti-symmetric str. |
| 3462 | 3 | no | symmetric str. |
| 3579 | 28 | yes | anti-symmetric str. |
| 3579 | 28 | yes | anti-symmetric str. |
NH3BH3 Calculations
ΔE = E(NH3) + E(BH3) - E(NH3BH3) = -56.55... - 26.61... + 83.22... = -0.051595..au
= -0.0516 au (3sf)
Hence Bond energy = 135 Kjmol-1 (3sf)
The end energy seems within the right region due to the fact a carbon-carbon bond is approximately 220Kjmol-1 it can be expected this dative bond will not be as strong. The fact it is dative mean the bond is non-symmetric hence electrons on average will be nearer the nitrogen this is expected as it's the lewis base and more electronegative. Literature value quotes and energy of 73.2 Kjmol-1 [1] this is significantly lower than expected likely due to the nature of approximations and error within the calculations of the software.
- ↑ Literature Data source DOI:10.1021/jp209712s ,http://www.ncbi.nlm.nih.gov/pubmed/22085293
Aromaticity Project
Benzene
Optimization
| Summary | Convergence | Jmol | ||||
|---|---|---|---|---|---|---|
Title Card Required File Name = Benzene_OPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -232.25820412 a.u. RMS Gradient Norm = 0.00009093 a.u. Imaginary Freq = Dipole Moment = 0.0001 Debye Point Group = C1 Job cpu time: 0 days 0 hours 1 minutes 51.0 seconds.File:Benzene opt summary.txt |
Item Value Threshold Converged?
Maximum Force 0.000198 0.000450 YES
RMS Force 0.000082 0.000300 YES
Maximum Displacement 0.000849 0.001800 YES
RMS Displacement 0.000305 0.001200 YES
Predicted change in Energy=-4.741882D-07
Optimization completed.
-- Stationary point found. File:CH BENZENE OPT.LOG |
|
Frequency Analysis
Low frequencies --- -13.7859 -12.9853 -11.8579 -0.0006 0.0005 0.0005 Low frequencies --- 414.0701 414.1914 620.9705
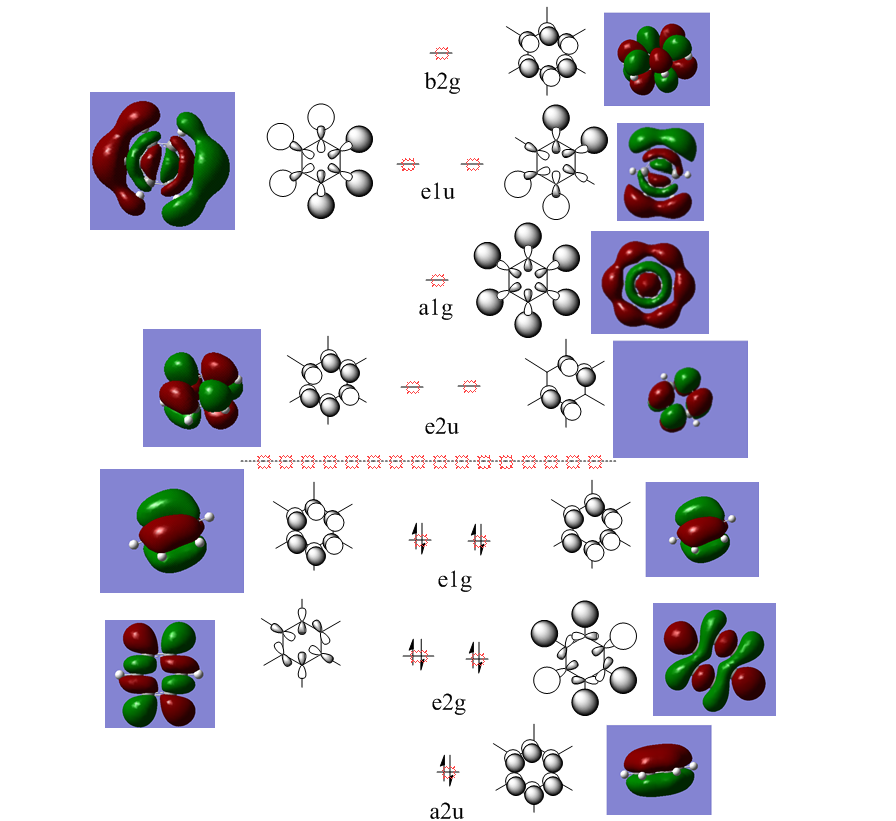
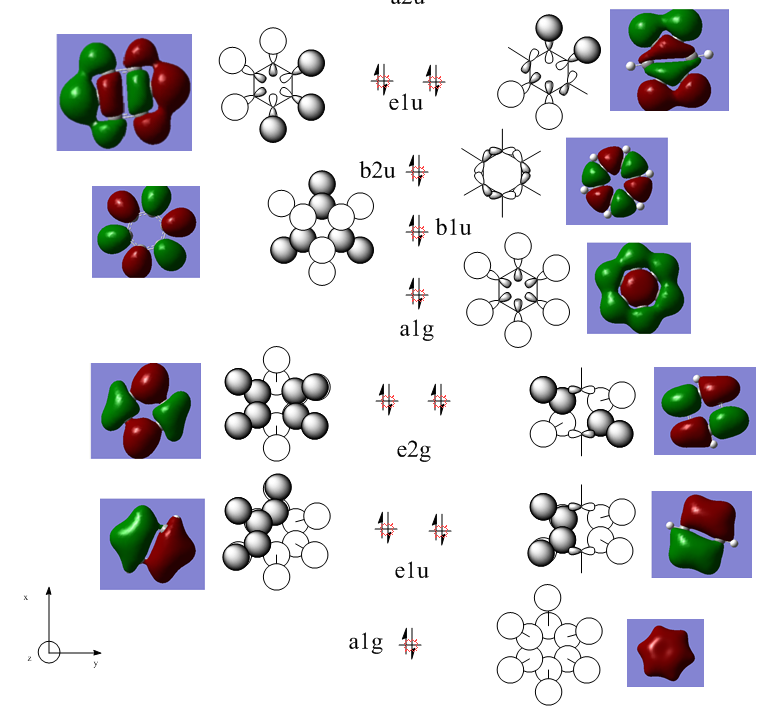
Molecular Orbital Analysis
How do the MO's relate to the conception of aromaticity?
Orbitals such as the a2u where all the carbon pz orbitals are aligned in phase show this best , the complete homogeneous overlap shows a even distribution of charge all around the ring. This is similar to the idea of resonance the previous method for describing the distribution of electron density in a molecule simply. Using MO's gives a calculated approach that indeed shows good agreement with previously established notions of the electronic benzene structure.
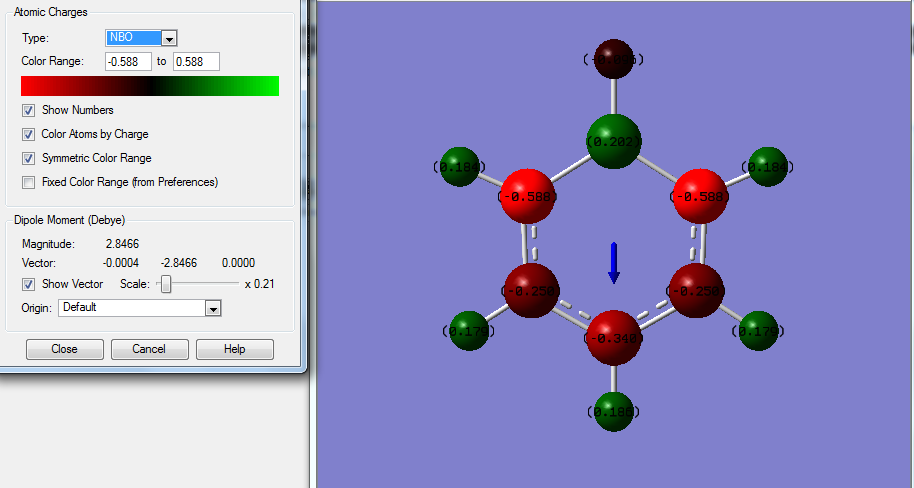
Boratabenzene
Optimization
| Summary | Convergence | Jmol | ||||
|---|---|---|---|---|---|---|
Borabenzene Optimization File Name = Borata_OPT_CH_output File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = -1 Spin = Singlet E(RB3LYP) = -219.02052227 a.u. RMS Gradient Norm = 0.00015828 a.u. Imaginary Freq = Dipole Moment = 2.8468 Debye Point Group = C1 Job cpu time: 0 days 0 hours 4 minutes 17.3 seconds.File:Borata opt summary CH.txt |
Item Value Threshold Converged?
Maximum Force 0.000160 0.000450 YES
RMS Force 0.000069 0.000300 YES
Maximum Displacement 0.000913 0.001800 YES
RMS Displacement 0.000331 0.001200 YES
Predicted change in Energy=-6.619385D-07
Optimization completed.
-- Stationary point found.
DOI:10042/31336 |
|
Frequency analysis
Low frequencies --- -6.6025 0.0002 0.0007 0.0007 4.1703 5.6230 Low frequencies --- 371.2575 404.5245 565.1709
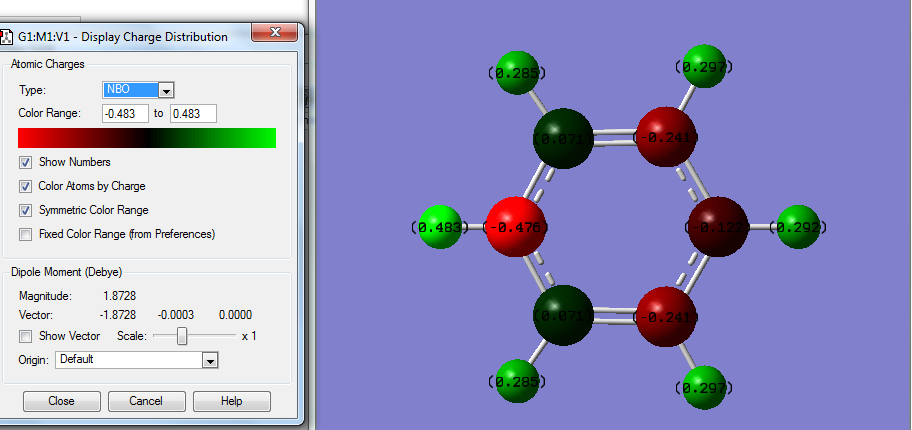
Pyridine
Optimization
| Summary | Convergence | Jmol | ||||
|---|---|---|---|---|---|---|
Title Card Required File Name = pyridine_OPT_output_CH File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 1 Spin = Singlet E(RB3LYP) = -248.66806084 a.u. RMS Gradient Norm = 0.00003908 a.u. Imaginary Freq = Dipole Moment = 1.8728 Debye Point Group = C1 Job cpu time:0 days 0 hours 4 minutes 8.6 seconds.File:Pyridine summary CH.txt |
Item Value Threshold Converged?
Maximum Force 0.000065 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.000792 0.001800 YES
RMS Displacement 0.000178 0.001200 YES
Predicted change in Energy=-7.076534D-08
Optimization completed.
-- Stationary point found.
DOI:10042//31337 |
|
Frequency analysis
Low frequencies --- -9.4930 -5.6067 -0.0013 -0.0003 0.0002 4.4714 Low frequencies --- 391.8972 404.3553 620.1952
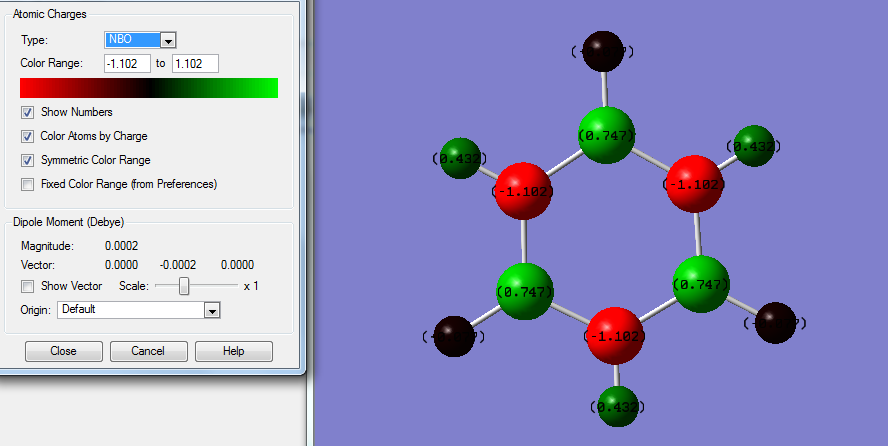
Borazine
Optimization
| Summary | Convergence | Jmol | ||||
|---|---|---|---|---|---|---|
Title Card Required File Name = pyridine_OPT_output_CH File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 1 Spin = Singlet E(RB3LYP) = -248.66806084 a.u. RMS Gradient Norm = 0.00003908 a.u. Imaginary Freq = Dipole Moment = 1.8728 Debye Point Group = C1 Job cpu time:0 days 0 hours 4 minutes 8.6 seconds.File:Borazine opt summary CH.txt |
Item Value Threshold Converged?
Maximum Force 0.000198 0.000450 YES
RMS Force 0.000082 0.000300 YES
Maximum Displacement 0.000849 0.001800 YES
RMS Displacement 0.000305 0.001200 YES
Predicted change in Energy=-4.741882D-07
Optimization completed.
-- Stationary point found. DOI:10042//31338 |
|
Frequency Analysis
Low frequencies --- 0.0003 0.0009 0.0010 3.1621 5.1149 8.4841 Low frequencies --- 289.6659 289.7981 404.4145
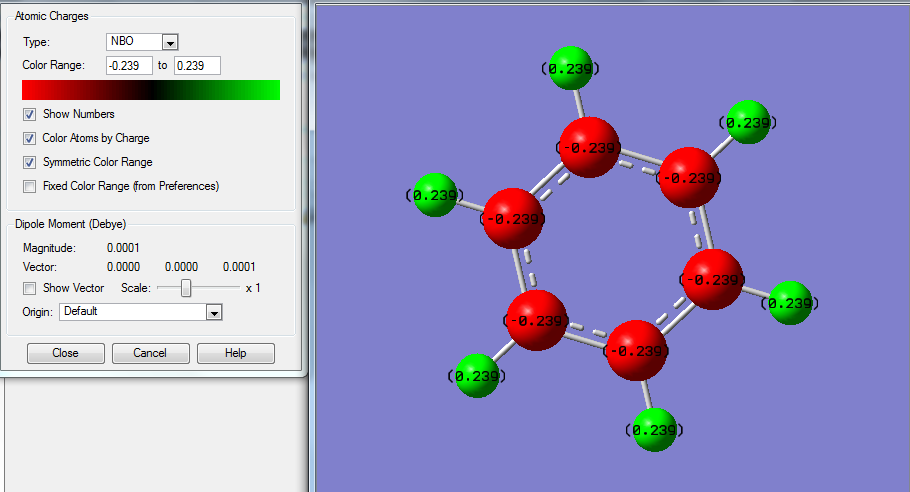
NBO Analysis & Comparison
| Atom | Benzene | Boratabenzene | Pyridine | Borazine |
|---|---|---|---|---|
| 1 | +0.239 | -0.096 | +0.483 | -0.077 |
| 2 | +0.239 | +0.184 | +0.285 | +0.432 |
| 3 | +0.239 | +0.179 | +0.297 | -0.077 |
| 4 | +0.239 | +0.186 | +0.292 | +0.432 |
| 5 | +0.239 | +0.179 | +0.297 | -0.077 |
| 6 | +0.239 | +0.184 | +0.285 | +0.432 |
| 7 | -0.239 | +0.202 | -0.476 | +0.747 |
| 8 | -0.239 | -0.588 | +0.071 | -1.102 |
| 9 | -0.239 | -0.250 | -0.241 | +0.747 |
| 10 | -0.239 | -0.340 | -0.122 | -1.102 |
| 11 | -0.239 | -0.250 | -0.241 | +0.747 |
| 12 | -0.239 | -0.588 | +0.071 | -1.102 |
The above data shows some interesting patterns, all is to be expected. Benzene shows a perfectly symmetric charge distribution with all carbons the same charge and all hydrogen's also the same again indicative of the highly symmetrical D6h structure. Borazine has a perfect alternating pattern of electronegativities this matches the nature of its D3h symmetry. The more symmetrical molecules such as benzene and borazine have no net dipole due to a lack of disproportion of charge density in the molecule. In the case of pyridine and boratabenzene this isn't the case. Boratabenzene unusually has the negative charge being imposed on the hydrogen connected to boron , this is one of the only scenarios where H carries the negative charge since boron is more electropositive. In both boratabenzene the symmetry breakdown leaves a range of different charge values as it becomes a C2v molecule the highest magnitude charged molecules are those connected to the B / N but the sign of these charges changes going from boron to Nitrogen since Nitrogen is electronegative and Boron positive. The net effect this has is a reversal of the dipole moment which is shown on the NBO analysis of boratabenzene , for pyridine the arrow is in the opposite direction.
Unusually in Boratabenzene the magnitude of the charge on the hydrogen attached to B is rather small (-0.096) in comparison to that of the adjacent Carbons to it (-0.588) this is likely due to the difference in the electronegativities of B (2.0) and H (2.1) compared to B (2.0) and C (2.5). A similar effect is shown by the nitrogen in pyridine the adjacent H being +0.483 and carbon being +0.071 since N has an electronegativity of 3.0 making it have a larger effect on H (2.1) due to the larger difference.
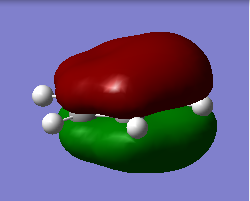
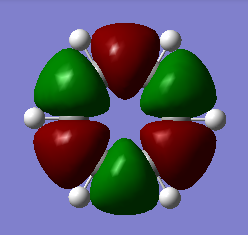
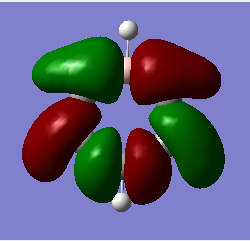
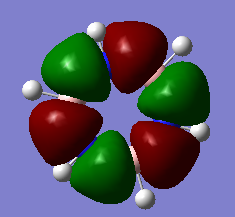
MO analysis & comparison
Above shown are 3 sets of 'equivalent' bonding orbitals from each compound.In the first set the all bonding p-orbitals are shown these are useful to show the localization of charge in the molecule. Benzene and borazine are quite similar due to symmetrical structures, although the center of borazine is slightly concave likely due to the more localized charges present from the polar bonds. Pyridinium and Boratabenzene the cloud is distorted in pyridinium most the density resides on the nitrogen for boratabenzene this is the opposite.
The second set is a partially anti-bonding MO compromised of 2S orbitals, this MO shows greatly the effect of the substitution of different atoms going from benzene to borazine. As a side note again the benzene and borazine molecules seem slightly unsymmetrical which is likely from not forcing the symmetry of the molecule. Within the second set there are many differences the main being the shape difference going from symmetrical more benzene/borazine to pyridinium/ boratabenzene. Interestingly going from benzene to boratabenzene their appearances are quite similar this is due to the fact that the boron 2S is too high in energy to interact with the 2S on the carbons hence the MO has a symmetry between the different phase lobes. For pyridinium this is not the case since nitrogen is lower in energy and sufficiently close to carbon in energy (and also within the periodic table). Another notable fact is that the selected orbitals for benzene and borazine are part of a degenerate pair this is not the same for pyridinium or boratabenzene this illustrates how the substitution causes a breakdown of symmetry hence degeneracy in the molecule.
A final difference is the ranking of the energy levels, these are in accordance with the previous calculations for the total energies; Benzene (-232.3 au) , Boratabenzene (-219.0 au), Pyridinium (-248.7 au) , Borazine (-242.7 au). In accordance with this the lowest orbital will be pyridinium followed by borazine , benzene and finally boratabenzene. The order can be rationalized from orbital contributions for instance in pyridinium a carbon is substituted for a nitrogen this atom is more electronegative / stable and is hence the orbitals on it are lower in energy. During the LCAO process this means combination with nitrogen will cause a net lowering in energy (more negative) of both bonding and anti-bonding orbitals and hence the net energy of the molecule is lower than benzene.The opposite is true for boratabenzene since it is electropositive and as shown in the second set causes different interactions as the 2S will not overlap with 2S on carbon. The case for borazine is somewhat different due to the fact it contains ionic contributions the best way this is shown is with the negative charge imposed on nitrogen and positive on the Boron. To further rationalize this a molecular orbital approach is best, boron and nitrogen have very different electronegativities. This means that although the splitting interaction is mild the initial difference in energy means the total deviation from the barycenter is still large, in fact larger than that show in benzene.
In the third set highlights how differences in the geometry effect the MO structure , they are all comprised of p-orbitals however in pyridinium and boratabenzene 2s also overlap. The addition of nitrogen distorts the ring with the bond length according to the data being; CN 1.352 and CC 1.383 this causes a distortion from the perfect hexagon which is why the p-orbital is able to interact with the s-orbital on hydrogen as it is no longer perfectly orthogonal to it which would not create an overlap.
The net effects of all these substitutions is to reduce the degeneracy thereby increasing the number of singular symmetry label MO's.