Rep:MOD:3VHW10
The Cope Rearrangement

The Cope Rearrangement(shown right) is the [3,3] Sigmatropic shift rearrangement of 1,5-Hexadiene (C6H10) under thermal conditions (6 electrons, 4n+2 system), where the system has some level of aromaticity in the transition state[1]. The aim of this study is to determine the reaction mechanism for the rearrangement by locating the low-energy minima and transition states of the molecule. The transition states (from literature[2]) of the molecule are shown left - it is currently accepted that the reaction occurs in a concerted fashion through a 'chair' or 'boat' transition structure, where the transition 'boat' has higher energy then the other state, by a few kcal/mol.
Optimisation of Reactants: 1,5-Hexadiene
The optimisations of suspected conformers (draw in Gauss View for the anti and gauche forms of 1,5 Hexadiene (for the four central atoms)) were run using the Hartree Fock method, with the basis set 3-21G (the %mem was specified as 250MB), and then data on the minimum energy and point group (symmetry) retrieved from the calculation.
1,5-Hexadiene can have different conformations with different associated minimum energies, due to stereo-electronic effects. Usually the gauche form of a molecule is expected to be of higher energy then the anti-conformer due to steric effects of the gauche subsituents. However, due to the medium length chain of this molecule and the double bonds in the system some gauche forms may be of lower energy then those in the anti conformation due to donation from the π orbital into an empty σ* orbital and also donation from the full σ orbital into the π* orbital when orbtials are of the correct orientation to overlap.[3]
Anti Conformer
The guessed anti-conformer was drawn in Gauss view (and the structure 'cleaned' before calculation) to give the optimised anti2 conformer shown in D-Space. The point group of the molecule and its energy (shown below) were compared to pre-calculated values[4], to confirm the molecule as the lowest energy anti-molecule (anti2). The energy calculated in this optimisation is the same as that referenced[4] for the same calculation - with a value of -231.69254 a.u. within the errors expected due to the iterative methods and approximations required for this calculation.
Point Group: Ci
Energy: -231.69252(528) a.u.
Conformation of Convergence: The convergence of the optimisation is shown below to confirm that the calculation has run to completion and a stationary point (i.e. the minimum energy) has been found, this proves the calculation has been completed.
Item Value Threshold Converged?
Maximum Force 0.000060 0.000450 YES
RMS Force 0.000010 0.000300 YES o
Maximum Displacement 0.000506 0.001800 YES
RMS Displacement 0.000171 0.001200 YES
Predicted change in Energy=-2.037270D-08
Optimization completed.
-- Stationary point found.Gauche Conformer
The assumed form of the lowest energy gauche-conformer was drawn in Gauss view (and the structure 'cleaned' before calculation) to give the optimised gauche3 conformer shown in D-Space. The energy and point group of the conformer upon calculation confirm the identity of the conformation as gauche3 (the lowest energy conformer), according to the data provided for this lab[4].
Point Group: C1
Energy: -231.69266(121) a.u.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000053 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.001612 0.001800 YES
RMS Displacement 0.000415 0.001200 YES
Predicted change in Energy=-9.816105D-09
Optimization completed.
-- Stationary point found.
Relative Energy of Conformations
The Anti-molecule is likely to be the lowest energy anti conformer due to stereoelectronic considerations, since the alignment of the central carbon chain allows for complete the anti-peri-planar conformation across the system (which is most stable due to staggered groups with the 180° dihedral angle between groups with the maximum number of σ(C-H)/σ*(C-H) overlaps allowed. Usually, in alkyl chains the anti-peri-planar arrangement is the lowest energy conformation, since no other effects occur to allow other interactions to become important (Van de Waals interactions, pauli repulsions), since bond overlap is most important in these systems. However, it is likely that there are other (possibly lower energy) anti conformations available to the molecule then the anti2 conformer calculated.
Since there are alkene 'substituents' at the end of the carbon chains it is possible (due to effects discussed above) for some gauche forms to have lower energies. Usually it is expected that the anti-peri-planar (app) conformation of any given molecule is the lowest energy due to steric considerations, however donation effects into the pi orbitals and hydrogen clashes/van der waals attractions certain gauche conformations give rise to lower energy conformations in this case.
It is likely that the Gauche conformer calculated is the lowest energy gauche conformer (confirmed from the data provided for this lab[4]) due to the maximisation of pi/sigma donations due to the alkene orbitals and van der waals attractions between hydrogens in the molecule, whilst reducing the amount of pauli repulsion between filled orbtials (σ(CH)/σ(CH)), as any conformations with more gauche forms is likely to give rise to a higher energy conformation. Therefore, no further calculations were done, as the lowest energy conformation of 1,5-Hexadiene was achieved.
Anti2 (Ci) Conformation
Higher Level Optimisation
The Ci (anti2) conformation of 1,5 hexadiene was located during the original optimisation and is therefore used in the second optimisation step (without any further calculations - since the conformer for analysis has been calcualted). The optimisation was run with the DFT B3LYP method, and the 6-31G* (6-31G (d)) basis set, to give the information in D-Space.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000219 0.001800 YES
RMS Displacement 0.000079 0.001200 YES
Predicted change in Energy=-1.588847D-08
Optimization completed.
-- Stationary point found.The overall geometry of the molecule changes very little upon calculation at a higher level, i.e. no bond angles or lengths deviate significantly, however there is a relative large change in energy for the conformer, (HF/3-21G, E=-231.69252(528) a.u.) of approximately ΔE= -2.91917752 a.u (or 1831 kcal/mol). Suggesting large variations in energy values for further calculations would have been observed if calculation had proceeded with the lower basis set.
Point Group: Ci
Energy: -234.6117(0280) a.u.
Frequency Analysis
The frequency calculation is run at the same level of theory as the optimisation file, B3LYP/6-31G* (DFT) with no solvation effects to give the files in D-Space. The frequency calculation is run to give the energy of the molecule on the potential energy surface, since the calculation carries additional terms required not present in the optimisation calculation.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000036 0.000450 YES
RMS Force 0.000013 0.000300 YES
Maximum Displacement 0.000228 0.001800 YES
RMS Displacement 0.000105 0.001200 YES
Predicted change in Energy=-1.509204D-08
Optimization completed.
-- Stationary point found.No negative frequencies are observed (below), which shows that all vibrations are real (no imaginary frequencies) as expected since this is the ground state conformation and not a transition state. The vibrational information can be used to calculate the expected infrared (IR) spectrum of the compound (shown below, right).
<center>Low frequencies --- -18.6344 -11.7127 0.0005 0.0006 0.0009 1.8427 Low frequencies --- 72.7326 80.1452 120.0243</center>

Energies (Thermochemistry):
The thermochemistry calculated under the frequency calculation outputs the energies of the molecule. Where the sum of electronic and zero-point energies is the potential energy at 0K (E=Eelec+ZPE), the sum of electronic and thermal free energies is the energy at 298.15K and 1 atm, including translations, rotational and vibrational energy modes (E=E+Evib+Erot+Etrans). The sum of electronic and thermal enthalpies is as above but contains a correct for RT (H=E+RT) and the sum of electronic and thermal free energies, containing a correction for free energy, the entropic contribution (G=H-TS).
- Sum of electronic and zero-point energies: 234.269212
- Sum of electronic and thermal energies: 234.461856
- Sum of electronic and thermal enthalpies: 234.460912
- Sum of electronic and thermal free energies: 234.500821
Optimisation of Chair/Boat Transition State Using Guess'
The transition states for the Cope Rearrangement are essentially a pair of C3H5 allyl fragments at a given distance apart with the 'boat'C2v (right) and 'chair' C2h(left) having observably different symmetry. Optimisations of the transition state can be done in several ways (discussed below) including calculation of force constants, using the redundant coordinate editor and using QST2. The reaction coordinates and the IRC (intrinsic reaction coordinate) can then be defined using the optimised transition structures.
The optimisation of an allyl fragment with the HF method and 3-21G basis set was published to D-Space. This optimised structure is essentially one half of the transition states and can therefore be used to build up the two transition states below, with approximatly 2.2A between the terminal ends of the allyl fragments.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000048 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.000155 0.001800 YES
RMS Displacement 0.000070 0.001200 YES
Predicted change in Energy=-1.277267D-08
Optimization completed.
-- Stationary point found.Optimising Chair Transition States
Transition states can be optimised manually; the negative direction of curvature (the reaction coordinate) is required. A reasonable guess of the transition structure geometry can be used to calcualte the force constant matrix (the 2nd derivative of the curve) and this structure is then optimised. If the guess structure is not similar to the exact structure then a different approach is used by freezing the reaction coordinate and minimising the molecule, once this is complete the coordinate is unfrozen and the transition state fully optimised. Both methods are used here, to give similar answers in terms of energetics and transition state geometries.
Chair Guess - Computing the Force Constant Matrix
The molecule guess (with the assumed transition states shown above) was optimised and frequencies calcualted (OPT+FREQ) manually, using Optimisation to a TS (Berny), force constants calculated ONCE and additionally OPT=NoEigen (since potentially more then one imaginary frequency is calculated), and the job published to D-Space.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000106 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.001713 0.001800 YES
RMS Displacement 0.000322 0.001200 YES
Predicted change in Energy=-1.775489D-07
Optimization completed.
-- Stationary point found.
<center>Low frequencies --- -817.7924 -5.4875 -4.4839 -1.5286 -0.0009 -0.0007 Low frequencies --- -0.0006 209.5419 396.0007</center>
The frequency calculation has run to completion with the lowest vibration being the imaginary frequency of 817.79cm-1, which shows the vibration corresponding to the Cope Rearrangement, i.e. the breaking of one bond whilst the formation of the bond at the opposing end of the allyl fragments takes place.
Bond Breaking/Making Distance: 2.02081 A
Chair Guess - Frozen Coordinate Method
The transition structure (the guess given above) was also calculated using the frozen coordinate method: the redundant Coord Editor was used to freeze the distance between the two parts of the transition state at a distance of approximately 2.2A (OPT=Redundant) and then optimized with the HF method at 3-21G level, and published to D-Space.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000106 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.001713 0.001800 YES
RMS Displacement 0.000322 0.001200 YES
Predicted change in Energy=-1.775489D-07
Optimization completed.
-- Stationary point found.
The .chk file was used for the optimised structure, which appears much as the transition optimised via the force constants, with bond forming/breaking distances at 2.2A. The Redundant Coord Editor was used to change the frozen bonds to derivative. The transition state was optimised as for the force constant method (but the normal guess Hessian (modified to include the two coordinates) is used. The calculation failed with the initial instructions and therefore upon discussion with a demonstrator the box, under General, Write Connectivity was unticked to allow completion of the calculation, to give the calculations in D-Space.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000037 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.001445 0.001800 YES
RMS Displacement 0.000222 0.001200 YES
Predicted change in Energy=-3.773799D-07
Optimization completed.
-- Stationary point found.One negative (imaginary) frequency is observed at -817.90cm-1, this value is comparable to the previous method.
<center>Low frequencies --- -817.9034 -0.0003 0.0004 0.0005 3.2177 4.6017 Low frequencies --- 4.6882 209.5958 395.8818</center>
Bond Breaking/Making Distance: 2.02006 A.
This value is comparable to the previous method, suggesting that the same TS has been achieved via both methods (since the TS guess is relatively close to the exact structure).
Optimising Boat Transition States
The boat transition structure is optimised using the QST2 method - where the reactants and products are specified and the calculation interpolates the structure to find the transition state between them. Therefore the reactant and product were numbered in the same way as shown below (for the rearrangement):
Anti2 was used for the product and reactant systems numbered in the same way as above. The calculation was a QST2, OPT+FREQ job with optimisation to a transition state TS(QST2). The job failed, giving this file in D-Space, where the structure calculated appears as the chair transition state but with more dissociation (as shown below), where the allyl fragment has been translated but not rotated.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000037 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.000919 0.001800 YES
RMS Displacement 0.000340 0.001200 YES
Predicted change in Energy=-3.124457D-07
Optimization completed.
-- Stationary point found.<center>Low frequencies --- -818.0136 -0.0024 -0.0014 0.0001 2.4031 4.8164 Low frequencies --- 4.9120 209.6578 396.1447</center>
The input file for the previous calculation was thus modified, so that the reactant and product geometries were closer to the boat transition structure. With the central dihedral angle at 0° and then inside angles at 100°, the QST2 calculation was then re-run, to give the structure in D-Space.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000105 0.000450 YES
RMS Force 0.000022 0.000300 YES
Maximum Displacement 0.001155 0.001800 YES
RMS Displacement 0.000256 0.001200 YES
Predicted change in Energy=-9.677516D-08
Optimization completed.
-- Stationary point found.Only 1 significant imaginary frequency (outside of the 6 from the 3N-6 vibrational modes) at -839.9283 cm-1 is observed, this vibrational motion is equivalent to the cope reaction as before for the chair transition state.
Low frequencies --- -839.9283 -8.0764 -6.3099 -4.0803 -0.0005 0.0007 Low frequencies --- 0.0009 155.0909 382.2138
Intrinsic Reaction Coordinate
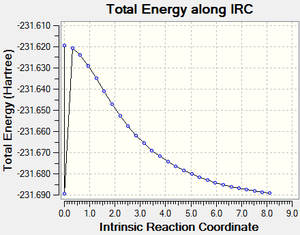
The Intrinsic reaction coordinate (IRC) follows the minimum energy path from the transition state to the local minimum (the product/reactant) on a potential energy surface, and therefore makes it possible to predict which conformer goes through which transitions state.

The frozen coordinate (derivative - 2nd step) chair transition state - was used for the IRC calculations - which were run in one direction (with the HF/321G method) since the reaction coordinates are the same in both directions and the force constants calculated only once (for time reasons) to give the following structure (in D-Space). The calculation ran to completion, however upon opening the file the calculation had completed less steps then requested on input and therefore terminated early. However, upon checking the IRC the system was moving with the correct distribution in the correct direction so the file was used to carry out an optimisation to find the minimum energy point - since the IRC did not find the minimum geometry (due to a lack of points under consideration). Other ways to get the calculation to run to completion (if further calculation was not to be done) would be increasing the maximum steps (more iterations per step) using MaxSteps=40 or recalculating the 2nd derivatives (force constants) to check the correct (shortest/steepest) path is being followed using ReCalc=10 (i.e. recalculating every 10 steps).
Energy: -231.68906206 a.u.
The IRC calculation was also run in both directions to confirm that the reaction as expected is symmetric, and this is confirmed in the image: here
All three methods of attaining the final minimum in the IRC were run and described below, since the original IRC calculation does not find the minimum geometry -
1. Minimisation (Optimisation) on the last point in the IRC
2. IRC with a larger number of points until the minimum is reached (plus an optimisation)
3. Computing the force constants at each step along the IRC.
However, there are problems with all of these approaches and as such the energies and structures of all methods are documented below. Since methods 1 and 2 can lead to the wrong minimum if too close to a minimum or if too many points are required respectively, however, approach 3 takes a long time (not always possible for larger systems).
| Method | Energy (Hartree) | Final (Product) Structure | Data Files |
|---|---|---|---|
| IRC with 50 Steps | -231.68906206 | D-Space | |
| Optimisation (HF/321G) | -231.69166702 | D-Space | |
| IRC with 100 Steps | -231.68906206 | D-Space | |
| Compute Force Constants at Every Step | -231.69157932 | D-Space |
The structures (shown above) at the minimum of the IRC suggest that the chair transition occurs when going from a gauche conformer (gauche2, due to the symmetry (c2) and structure)[4] to a gauche conformer (since the reaction is symmetric in both directions).
Activation Energies
The activation energies of the transitions structures can be calculated from the energies outputted from reoptimisation at the B3LYP/6-31G* (DFT) level and carrying out frequency calculations. The HF/3-21G optimised structures were used to complete the calculations.
Chair TS : Optimisation:
For the chair TS the frozen coordinate method HF/3-21G structure was used for further optimisation, to give a structure with similar geometry but with a slightly larger energy (more stable) then with the previous optimisation method in D-Space.
Energy: -234.55698311 a.u.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000050 0.000450 YES
RMS Force 0.000014 0.000300 YES
Maximum Displacement 0.001721 0.001800 YES
RMS Displacement 0.000360 0.001200 YES
Predicted change in Energy=-2.862503D-07
Optimization completed.
-- Stationary point found.Frequency Analysis:
The frequency analysis was completed with the B3LYP/6-31G* basis set, at the same level as the optimisation calculation to give the structure shown below in D-Space, the energy is the same as the Optimisation energy showing the same structure has been found and therefore the calculation ran correctly.
Energy: -234.55698311 a.u.
Conformation of Convergence:
Item Value Threshold Converged? Maximum Force 0.000157 0.000450 YES RMS Force 0.000050 0.000300 YES Maximum Displacement 0.002305 0.001800 NO RMS Displacement 0.000710 0.001200 YES Predicted change in Energy=-1.188179D-06
Although the displacement does not fully converge this is allowed since the value is only slightly outside the threshold and more importantly the forces have converged, and since the previous optimisation is converged the correct geometry has been obtained. There is one appreciable low frequency, corresponding to the cope rearrangement as before at -565cm-1
Low frequencies --- -565.6886 -0.0003 0.0004 0.0008 22.1626 27.3558 Low frequencies --- 39.7847 194.5197 267.8518
Energies (Thermochemistry): The thermochemsitry of the transition state at 298K is obtained through the frequency calculation, and shown below:
- Sum of electronic and zero-point energies: 234.414931
- Sum of electronic and thermal energies: 324.409010
- Sum of electronic and thermal enthalpies: 234.408066
- Sum of electronic and thermal free energies: 234.443816
Boat TS: Optimisation:
The boat optimisation was run with the B3LYP/6-31G method/basis set to find the transition state (TSBerny), force constants were calculated once and the key word opt=ModRedundant to allow the calculation to run to completion. All previous attempts to calculate a minimum gave rise to calculation of the product/reactant since this is the lowest energy state. The calculation is shown in D-Space. There energy is larger then for the HF method, but closer to known values stated in the laboratory script [4].
Energy: -234.54309295 a.u.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000026 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.001532 0.001800 YES
RMS Displacement 0.000281 0.001200 YES
Predicted change in Energy=-1.255481D-07
Optimization completed.
-- Stationary point found.Frequency Analysis:
The frequency analysis for the boat transition state were calculated as above for the chair transition state to give the structure below in D-Space. The energy is the same as the optimisation energy showing that the same geometry has been calculated and therefore the calculation has run to completion. One imaginary frequency is found, expected for the transition state, and resonates with a similar frequency range to the chair transition state and corresponds to the cope rearrangement.
Energy: -234.54309295 a.u.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000107 0.000450 YES
RMS Force 0.000035 0.000300 YES
Maximum Displacement 0.001519 0.001800 YES
RMS Displacement 0.000507 0.001200 YES
Predicted change in Energy=-2.924118D-07
Optimization completed.
-- Stationary point found.Low frequencies --- -529.7200 -8.9582 -0.0006 0.0004 0.0005 15.5293 Low frequencies --- 17.8047 135.5985 261.5047
Energies (Thermochemistry): at 298.15K (standard T,p)
- Sum of electronic and zero-point energies: 234.402348
- Sum of electronic and thermal energies: 324.396012
- Sum of electronic and thermal enthalpies: 234.395067
- Sum of electronic and thermal free energies: 234.431760
Energy Comparisons
| Structure | HF/321-G (hartree) | B3LYP/6-31G* (hartree) | Activation Energy, ΔE (kcal/mol) |
|---|---|---|---|
| Boat TS | -231.60280239 | -234.54309295 | 43.053(29836365) |
| Chair TS | -231.61932111 | -234.55698311 | 34.337(09795221) |
| Anti2 (reactant) | -231.69252528 | -234.61170280 | --- |
* Energies shown in hartree (a.u.) where 1 hartree = 627.509 kcal/mol, all energy values are at 0K.
In all cases, the geometries of the transitions states vary very little upon further optimisation at the higher level, however as shown in the table above there is a large variation in the energies of the same conformer/transition state using different calculation methods. The energies calculated are similar to experimental data[4] at 0K, within the error stated, some of these errors are likely to be due to the iterative nature of the calculation and the low level basis sets used. It can be seen here that the activation energy to proceed via the chair transition state, likely because this state is less hindered (since the hydrogens in opposing fragments are staggered and so less steric clashes occur) as discussed in literature[5] (with similar energies calculated).
There is likely to be some error in this comparison since the conformer under calculation is the anti2 reactant (product) whereas, from the IRC calculations, it can be seen that the reactant/product going through the chair transition state (and under such as assumption the chair) is the gauche2 conformer, which will have slightly different energies associated with it (since it is a higher energy conformer). This will give rise to some of the errors seen upon calculation of the activation energies.
Diels Alder Cycloaddition
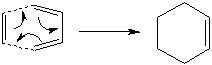
Diels-Alder reactions are pericyclic reactions[6] where the reaction is concerted with no intermediates, and the transition states have an aromatic character. A Diels-Alder reaction is a form of cycloaddition between a conjugated diene (in this s-cis conformation) and an alkene (dienophile), where two pi bonds are broken and two sigma bonds are formed.
The reaction is either allowed or forbidden due to specific rules dependant on the number of electrons and the symmetry of the frontier molecular orbitals taking part in the reaction. The electron count for the system is 6 (4n+2, n=1, showing aromaticity according the Huckel), and the reaction may only proceed if symmetry is conserved. [1]
Diels Alder Reaction: Butadiene and Ethene
Optimisation of Butadiene
The butadiene molecule, in the cis conformation (here) was optimised using the semi-empirical molecular orbital AM1 method, and published to D-Space.
Energy: 0.04879719 a.u. (30.621 kcal/mol)
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000030 0.000450 YES
RMS Force 0.000011 0.000300 YES
Maximum Displacement 0.000407 0.001800 YES
RMS Displacement 0.000162 0.001200 YES
Predicted change in Energy=-9.683172D-09
Optimization completed.
-- Stationary point found.Determining Symmetry:
The total symmetry of the molecule (found using symmetrise) is C2v. For the Diels-Alder reaction the symmetry of the molecular orbitals which are donating or accepting electrons are important and as such the orbitals are visualised to confirm their symmetry with respect to the plane through the centre of the molecule, between carbon atoms 2 and 3 (shown right).
| HOMO (11) | LUMO (12) |
|---|---|
 |

|
| Anti-symmetric wrt. plane | Symmetric wrt. plane |
Calculation of Transition State
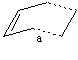
The transition state was calculated using the guess (shown right) - an envolope structure that gives good overlap between the incoming pi orbitals of the ethylene molecule and the pi system of butadiene.
The frozen coordinate method was used with the C-C bonds (shown) frozen at a given length, a after the guess was cleaned, the calculation was run with the semi-empiricial method with AM1 basis set and optimised to a minimum with the key word opt=ModRedundant and the un-write connectivity not imposed. The first optimisation was a poor guess, with low symmetry (a problem for the symmetry requirements of the reaction) and therefore symmetrisation was run of the molecule for following steps (Default(0.001)) to give a symmetrical transition state.The following steps of optimisation are shown in the table below:
| Frozen Bond Distance (a) / A | Optimised Structure | Files Run | Comments |
|---|---|---|---|
| 1.8 |  |
D-Space | Poor Guess for Transition State Geometry - Low symmetry compared to requirements for Diels-Alder (did not converge) |
| 2.0 |  |
D-Space | Poor Guess for Transition State Geometry - as before (symmetrise required for following calculations) |
| 2.2 (as in prev. calcs) |  |
D-Space | Appears close to expected transition state with ethene fragment approaching from above butadiene fragment as required by symmetry constraints (begins formation of new double bond in product) |
Therefore, since the geometry calculated is similar to that expected from the transition state of this reaction, with the symmetry constraints imposed. The final optimisation with bond lengths a=2.2A was used for further calculation with the bonds unfrozen to calculate the transition state, after the geometry had been confirmed as converged (below).
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000044 0.000450 YES
RMS Force 0.000014 0.000300 YES
Maximum Displacement 0.001478 0.001800 YES
RMS Displacement 0.000278 0.001200 YES
Predicted change in Energy=-4.728388D-07
Optimization completed.
-- Stationary point found.
To complete the optimisation of the transition state the bonds at the 2.2A guess were unfrozen (using the derivative instead of frozen) and an OPT+FREQ calculation was run with optimisation to a transition state (Berny), calculating force constants never and using the semi-empirical AM1 method. The resultant structure can be found in D-Space, and the geometry of the transition state shown right.
Energy: 0.11165524 a.u. (70.06 kcal/mol)
Bond length of partially formed σ C-C bond in TS: 2.11925 A
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000120 0.000450 YES
RMS Force 0.000015 0.000300 YES
Maximum Displacement 0.001388 0.001800 YES
RMS Displacement 0.000232 0.001200 YES
Predicted change in Energy=-2.605494D-07
Optimization completed.
-- Stationary point found.There is one imaginary frequency, showing that a transition state has been located, the vibration is equivalent to the diels alder reaction - the approach of the two ends of the diene and dienophile system to give the cyclohexene structure.
Low frequencies --- -955.9388 -4.7672 -4.2940 -0.0031 0.0058 0.0309 Low frequencies --- 5.7462 147.0101 246.6429 ****** 1 imaginary frequencies (negative Signs) ******
Discussion
Transition Structure

The geometry of the transition state is shown (right), with the ethene molecule approaching face on to the butadiene molecule - either from above or below the plane of the molecule. This is due to symmetry considerations as discussed below, allowing orbtials of the correct symmetry to interact to allow bond formation, since in this reaction two new sigma bonds are formed between the terminal ends of the butadiene molecule and the two carbon atoms in the ethene molecule.
The bond length of the partially formed σ C-C bond in the transition state are 2.11925 Å.
The typical bond lengths of C-C bonds in alkyl substrates are shown below[7]:
C-C sp3-sp3: 1.53 Å
C-C sp2-sp2: 1.46 Å
The Van der Waals radius of carbon is 1.70Å[8]
The C-C bond length of the partly formed σ C-C bonds in the TS is within twice the VdW radius of a carbon atom, which shows that the orbitals of the atom are able to interact and therefore there is bonding character between the atoms in the transition state. However, the partially formed bond length is much longer then that of typical stable molecule, and therefore bond formation is not complete in this transition structure - hence the bonds are much longer then standard bond lengths in carbon systems.
Reaction Pathway
The vibration corresponding to the reaction pathway at the transition state is shown below - it shows the formation of 2 new sigma bonds between the terminal carbons of the cis-butadiene and the ethene. The vibration shows that bond forming is synchronous (i.e. both bonds are formed at the same time, with the same rate) to give the product of the reaction.
| Imaginary Frquency (-956 cm-1) | Lowest Positive Frequency (147 cm-1) | ||||||
|---|---|---|---|---|---|---|---|
|
|
The imaginary (negative) frequency corresponds to the reaction pathway at the transition state giving rise to the product of the Diels Alder reaction between ethene and cis-butadiene. However, the lowest positive frequency corresponds to the motion of the two components separately, with low energy motions both in and out of the plane of the molecule - with the ethene hydrogens showing an asymmetric stretching motion and more complex vibrational motions in the butadiene fragment. There is no major interaction between the two fragments, hence the difference between the imaginary and real frequencies - one is a reaction pathway with interaction of the two fragments whilst the other shows independant molecular vibrations.
Molecular Orbitals
The frontier molecular orbitals of the transition state for the diels alder reaction between ethene and cis-butadiene are shown below:
The HOMO at the transition structure is a (anti-symmetric), which is as expected since the final product of the diels-alder reaction is antisymmetric (in terms of molecular orbtials). The MOs that form the product are the HOMO of the butadiene molecule (a) and the LUMO of the ethene molecule (a), to give the anti-symmetric transition state calculated here. The reaction is allowed since the HOMO of butadiene reacts with the LUMO of ethene resulting in the formation of 2 new sigma bonds in the final product, this reaction is allowed since orbital symmetry is conserved in the reaction.
Regioselecivity in the Diels-Alder Reaction: Cyclohexa-1,3-Diene and Maleic Anhydride
When the dienophilie in a Diels-Alder reaction is substituted, if the substitutent has pi orbitals then it can interact with the double bond formed in the product and stabalise the regio-chemistry. In general the diels-alder reaction only occurs if there is an electron withdrawing group on the dienophilie[6] amd as such the reaction between ethylene and butadiene is poor (although proceeds in theory, according to the claculations above). The transition state for reactants can be used to probe the reaction for the cases where either the diene and/or the dienophile have substituents (secondary orbtial affects), as shown below.

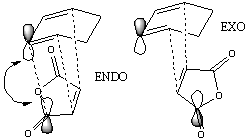
Cyclohexa-1,3-diene and maleic anhydride react (right) to give mainly the endo- adduct, the reaction is under kinetic control so therefore the exo transition state should be higher in energy.
The transition states for the Exo and Endo were calculated using the Frozen Coordinate Method. Freezing the forming bonds (shown by dashed lines in diagrams) at 2.2Å (as for other calculations - since this length is much longer then C-C bond formation lengths). The optimisation on the frozen structure was run with the semi-empirical AM1 method and optimism to a minimum (with the key word opt=ModRedundant - reading the frozen coordinates from the redundant coordinate editor).
To complete the calculation and find the transition state of the regio-isomer the frozen bonds were unfrozen and derivatives (Hessian) applied to them, the OPT+FREQ calculation with the AM1 (and then at the higher HF/3-21G level) method was run to a TS(Berny) with the force constants calculated once and the key words NoEigen.
Calculation of the Exo Transition State
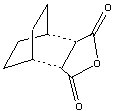
The transition state corresponding to the Exo product was calculated using a guess shown here, using the guess structure(right) using the method specified above, with the calculated geometry (minimum energy for the molecule with frozen bonds) shown in D-Space. The geometry appears similar to the expected TS (with the maleic anhydride approaching the system from above (with the correct alinement and symmetry as required for a permitted cyclo-addition), therefore this geometry was used to proceed to unfreeze and fully optimise the molecule to the transition state.
Conformation of Convergence, for the Frozen Bond Exo Transition State:
Item Value Threshold Converged?
Maximum Force 0.000016 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.001035 0.001800 YES
RMS Displacement 0.000167 0.001200 YES
Predicted change in Energy=-2.081525D-08
Optimization completed.
-- Stationary point found.HF/321G: Unfreezing the Bonds and Optimising to a Transition State (TS Berny).
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000112 0.000450 YES
RMS Force 0.000014 0.000300 YES
Maximum Displacement 0.001789 0.001800 YES
RMS Displacement 0.000305 0.001200 YES
Predicted change in Energy=-2.996821D-07
Optimization completed.
-- Stationary point found.Low Frequencies:
Low frequencies --- -646.7159 -5.6867 -4.1664 -3.0435 -0.0007 -0.0006 Low frequencies --- 0.0005 41.4981 131.1741 ****** 1 imaginary frequencies (negative Signs) ******
Calculation of the Endo Transition State

The Endo transition state was calculated using the guess here (shown right) and the calculation method discussed above, with the final geometry published to D-Space. Since the geometry appears as expected for the transition state this optimisation was then used to calculate the final transition state - since the maleic anhydride shows approach from the correct orientation with the overlap expected between the C=O pi orbitals and the double bonds of the diene, which is opposed to the transition state calculated for the exo structure and fits with known theories on regioselectivity in Diels-Alder reactions.
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000002 0.000300 YES
Maximum Displacement 0.000888 0.001800 YES
RMS Displacement 0.000113 0.001200 YES
Predicted change in Energy=-7.781784D-09
Optimization completed.
-- Stationary point found.HF/321G: Unfreezing the Bonds and Optimising to a Transition State (TS Berny).
Conformation of Convergence:
Item Value Threshold Converged?
Maximum Force 0.000131 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.001543 0.001800 YES
RMS Displacement 0.000251 0.001200 YES
Predicted change in Energy=-2.674680D-07
Optimization completed.
-- Stationary point found.Low Frequencies:
Low frequencies --- -642.3527 0.0006 0.0007 0.0008 2.3922 2.5300 Low frequencies --- 5.0917 65.2724 142.0274 ****** 1 imaginary frequencies (negative Signs) ******
Endo v.s. Exo Regioisomers
| EXO | ENDO | |||||||
|---|---|---|---|---|---|---|---|---|
| D-Space | ||||||||
| HF Energy | ||||||||
| AM1 Energy | ||||||||
| Relative Energy | ||||||||
| Bond Lengths | 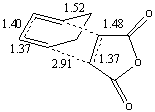 |
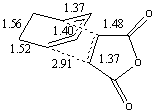 | ||||||
| Forming Bond Length in TS (Å) | ||||||||
| Through Space C-O Bond (Å) | ||||||||
| Transition Structure | ||||||||
| Imaginary Frequency (cm-1) | ||||||||
| Vibration (Reaction Pathway) |
|
| ||||||
| HOMO | 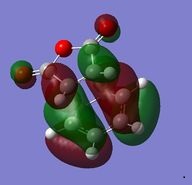 |
 | ||||||
| LUMO | 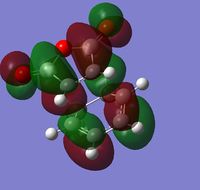 |
 |
Discussion
The preferred structure is dependent on variations in strain and steric repulsion (angle strain and through steric hindrance) for the two isomers versus the secondary orbital interactions possible between the pi system of the -CH=CH- and -(C=O)-O-(C=O)- fragment of the endo isomer. The strain in the exo form is likely to be more due to steric clashes between the oxygen atoms on the maleic anhydride and the carbons in the -CH2-CH2- carbon bridge, this is not present in the Endo isomer due to the geometry of the transition state. The structural differences between the exo and endo forms are due to the approach of the maleic anhydride from the -CH=CH- end of the diene in the endo isomer as opposed to approach from the -CH2-CH2- end of the diene in the exo isomer, this gives rise to the steric clashes (as discussed above) observed in the exo isomer, which aren't observed in the endo isomer since there is no possible interaction between the C=O bonds and the carbon bridge to prevent the approach of the dieneophile. This accounts for the approach of the dienophile being closer (2.8A as opposed to 2.9A in the exo isomer) to the diene in the transition state. The bond lengths (shown in the table above) for the two isomers show very little variation in the carbon framework (and are in good agreement with higher level calculations in literature[9]), although the through space distances and the length of the forming sigma bonds are shorter in the endo transition state (i.e. they are further towards formation then the exo state since they are shorter), since this is a lower energy route.
The relative energies of the endo(0.0000) and exo (0.0068) regio-isomers show that the endo transition state and therefore the endo product is the lowest in energy and therefore kinetically preferred product for the reaction (since the transition state is lower in energy and therefore less energy is required to pass through this step to the product) - determined by the steric hindrance in the transition states as well as secondary orbital overlap effects present only in the Endo isomer. The HOMO orbitals of the endo and exo orbitals (shown in the table above) both show a single node between the HOMO of the diene (a) and the LUMO (a) of the dienophilie to give an overall antisymmetric orbital (fitting the orbital requirements for this type of cycloaddition). The HOMO between the -(C=O)-O-(C=O)- fragment and the rest of the system however can be analysised to determine the 'secondary orbital overlap effect' which gives rise to the preference for the endo isomer over the exo isomer in Diels-Alder reactions[10] (here the sterics effects also give rise to the preference for the endo isomer). The secondary orbital interactions visualized right, can be observed in the HOMO of the endo and exo structures. In the endo structure there is the possibility for overlap between an orbital on carbon of the -CH=CH- fragment and an orbital on the carbon of the C=O bond in maleic anhydride, seen as visible electron density in this region, however this is not possible for the exo structure which is confirmed by no electron density being observed in this region. This bonding type overlap (at a closer distance for the endo isomer) gives rise to a stabilization of the transition state giving rise to the endo isomer as the kinetic (formed) product in this pericyclic reaction. Some effects have been neglected in these calculations.
References
- ↑ 1.0 1.1 H. Rzepa., (2012)., Pericyclic Reactions., [Lecture]., Imperial College London., Spring 2012
- ↑ O.Wiest, K.A.Black, K.N.Houk., Density Functional Theory Isotope Effects and Activiation Energies for the Cope and Claisen Rearrangements., J. Am. Chem. Soc., 1994, 116 (22) pp 10336-10337., DOI:10.1021/ja00101a078
- ↑ H. Rzepa., (2012)., Conformational Analysis., [Lecture]., Imperial College London., Spring 2012
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 M.Bearpark., (2012)., Moecule 3, Physical (Computational Lab)., [Lab Script]., Imperial College London., Autumn 2012., Lab Script
- ↑ K. Morokuma, W.T. Borden, D.A. Hrovat., Chair and Boat Transition States for the Cope Rearrangement. A CASSCF study., J. Am. Chem. Soc., 1988, 110 (13) pp 4474-4475., DOI:10.1021/ja00221a092
- ↑ 6.0 6.1 Clayden, Greeves, Warren, Worthers., Organic Chemistry., London: OUP., 2009.,
- ↑ F.H. Allen, O. Kennard, D.G. Watson, et.al., Tables of Bond Lengths determined by X-Ray and Neutron Diffraction. Part 1. Bond Lengths in Organic Compounds., J. Chem. Soc. Perkin Trans. 2., 1987, S1-S19., DOI:10.1039/P298700000S1
- ↑ A. Bondi., Van der Waals Volumes and Radii., J. Phys. Chem., 1964, 68 (3) pp 441-451., DOI:10.1021/j100785a001
- ↑ D. Birney, T.L. Lim, J.H. Koh, et.al., Structural Investigations into the retro-Diels Alder reaction. Experimental and Theoretical Studies., J. Am. Chem. Soc., 2002, 124 (18) pp 5091-5099., DOI:10.1021/ja025634
- ↑ C. Braddock., (2011)., Alkanes, Alkenes & Alkynes., [Lecture]., Imperial College London., Spring 2011


