Rep:MOD:3817fhp
Molecular Modelling 2
NH3 Molecule
Summary Information
What is the molecule? NH3
What is the calculation method? RB3LYP
What is the base set? 6-31G(d,p)
What is the final energy E(RB3lYP) in atomic units (au)? -56.55776873
What is the RMS gradient (au)? 0.00000485
What is the point group of your molecule? C3V
What is the optimised NH bond distance( Å )? 1.01798
What is the optimised NH bond angle(degrees)? 105.741
Item Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
NH3 molecule |
The optimisation file is linked to here
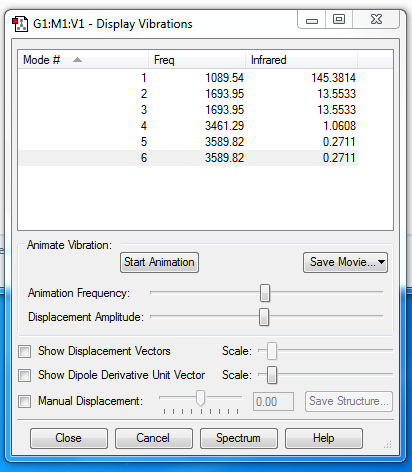
Vibrational Modes
The frequency is in Hz
Description of modes
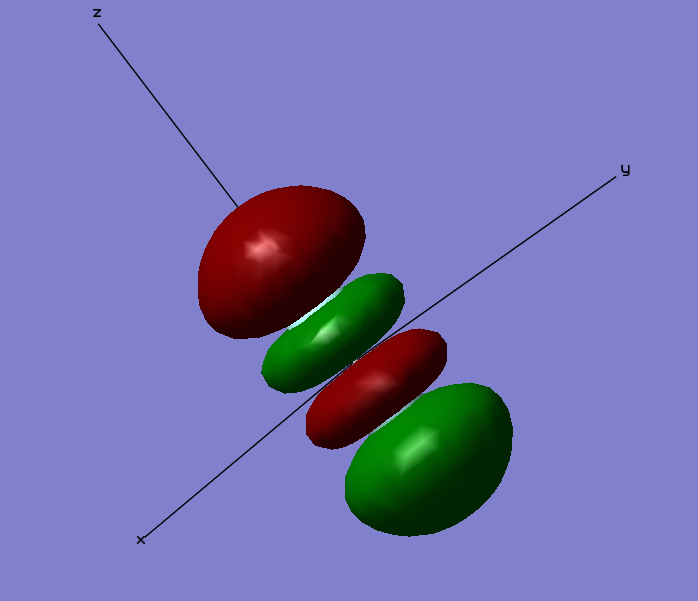
Mode 1 - N-H wagging (change in dipole moment: active)
Mode 2 - H-N-H scissoring (change in dipole moment: active)
Mode 3 - H-N-H scissoring (change in dipole moment: active)
Mode 4 - N-H symmetric stretching (change in dipole moment: active)
Mode 5- N-H asymmetric stretching (change in dipole moment: active)
Mode 6 - N-H asymmetric stretching (change in dipole moment: active)
How many modes do you expect from the 3N-6 rule? 3(4)-6 = 6
Which modes are degenerate? Using the mode numbers on the Display Vibrations Window, Modes 2 and 3 are degenerate and modes 5 and 6 are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations? Bending Vibrations:1,2 and 3. Bond Stretch Vibrations = 4,5 and 6.
Which mode is highly symmetric?Mode 4
One mode is known as the "umbrella" mode, which one is this? Mode 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia? You would expect to see 4 vibration modes for ammonia spectrum. Although there are 6 modes reported, there are two degenerate pairs therefore only 4 modes will be observed as peaks. There are 2 degenerate stretches and two degenerate bends.
Charge Analysis
The charge of Nitrogen atom: -1.125 The charge on the Hydrogen atom: 0.375
You would expect the nitrogen atom to have a negative charge as it is the more electronegative atom. Likewise you would expect the charge on the Hydrogen to be positive as it is more electropositive. Therefore our results fit with what was expected.
N2 Molecule
Summary Information
What is the molecule? N2
What is the calculation method? RB3LYP
What is the base set? 6-31G(d,p)
What is the final energy E(RB3lYP) in atomic units (au)? -109.52412868
What is the RMS gradient(au)? 0.00000060
What is the point group of your molecule? D∞h
What is the optimised NN bond distance(Å)? 1.10550
What is the optimised NN bond angle(degrees)? 180
Item Table
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
N2 molecule |
The optimisation file is linked to here
Frequency Analysis
Vibrational Frequency: 2457.33. This is a positive number therefore the molecule is fully optimised.
H2 molecule
summary Information
What is the molecule? H2
What is the calculation method? RB3LYP
What is the base set? 6-31G(d,p)
What is the final energy E(RB3lYP) in atomic units (au)? -1.17853936
What is the RMS gradient(au)? 0.00000017
What is the point group of your molecule? D∞h
What is the optimised HH bond distance( Å )? 0.74279
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
H2 molecule |
The optimisation file is linked to here
Frequency Analysis
Vibrational frequency: 4465.68 This is a positive energy value therefore the molecule i is fully optimised.
Haber-Bosch Reaction
Determining the Energy of Reaction using computer calculated values
This was converted from hartree to kJmol-1 using an online energy converter
Energy Analysis
The energy change for the reaction is negative therefore energy is given out (exothermic). The product (gaseous ammonia) is more stable than the reactants (gaseous hydrogen and ammonia) as it exists at a lower energy state.
Project Molecule - F2
Summary Information
What is the molecule? F2
What is the calculation method? RB3LYP
What is the base set? 6-31G(d,p)
What is the final energy E(RB3lYP) in atomic units (au)? -199.49825218
What is the RMS gradient (au)?0.00007365
What is the point group of your molecule? D∞h
What is the optimised FF bond distance( Å )? 1.40281
Item Table
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES
F2 molecule |
The optimisation file is linked to here
Frequency Analysis
Vibrational Frequency: 1065.09. This is a positive value showing that the molecule is fully optimised.
Vibrational information
There is only one vibration for my linear F2 molecule. This is a symmetrical stretch with a frequency of 1065.09.
Charge information
There is no charge on either of my F atoms in the F2 molecule. This is because the atoms are the same therefore, even though Flourine is the most electronegative atom and would usually hold a negative charge, there is no charge interactions between the two atoms. Therefore overall each atom has no charge.
Molecular oribital Information
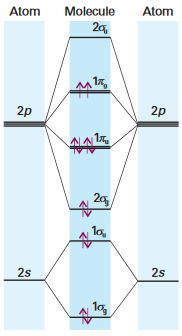
Molecular Orbital Diagrams
Referring to a standard molecular orbital diagram aids in the understanding and explanation of the MO diagrams. Note: the molecular orbital diagram shown does not contain
Source: P.Atkins and J. de Paula, 'Molecular Structure: Homonuclear Diatomic Molecules', in Atkins Physical Chemistry, Oxford University Press, Oxford UK, 8th edition, 2006, Chapter 11, 366
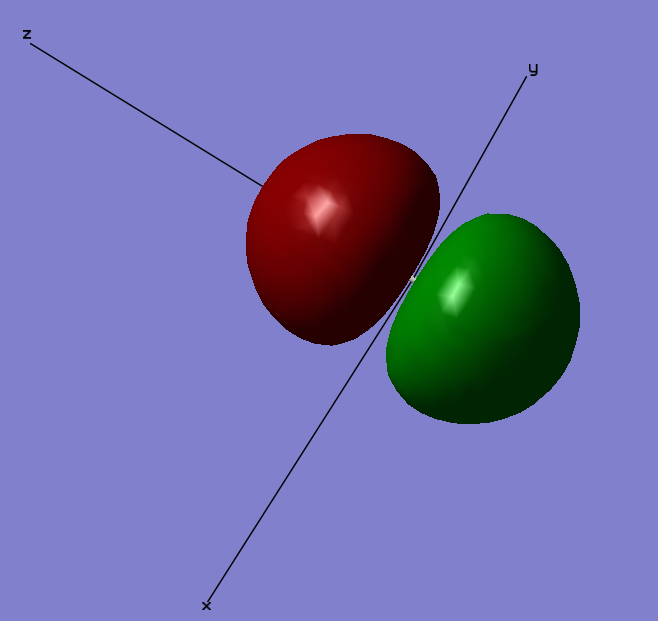
Axis Definition
The definition of the Cartesian axis also aids in the description of the MO diagrams. Here the bonding axis is defined as the z axis with the x and y axis being orthogonal to this.
1 σ (1s) Bonding Orbital
This orbital is the 1 σ g orbital formed as result of the constructive overlap of the two 1s orbitals of the F atoms. It is difficult to make out the orbital in the image as it is covered by the ball of the F atom. This is because the 1 σ MO's are considered to be core orbitals. They are so deep in energy their involvement in the bonding and interaction of the two atoms is very small. Their relative energy lies at -24.79730 compared to -1.33659 of the 2 σ orbitals
1 σ (2s) Antibonding orbital
This orbital is the 2s σ antibonding orbital. This orbital is formed as a result of the destructive overlap of two 2s orbitals of opposite phase. This antibonding orbital is occupied by 2 electrons. As it is a σ orbital there are no nodes along the bonding (Z) axis, however there is one node orthogonal to the z axis in the middle of the bond. Here the bonding electrons have a high probability of occupying space therefore there is a low probability of finding the antibonding electrons within this area. As an antibonding orbital it has a destabilising effect on the energy of the molecule as the presence of electrons within this bond increases the probability of electrons being found outside of the bonding region. Its energy lies higher than that of its corresponding bonding orbital.
2 σ 2pz g Bonding Orbital
This orbital is the 2 σ g orbital. This orbital is formed as a result of the constructive overlap of two 2p orbitals along the same axis i.e. two 2pz orbitals; one from each Flourine atom. This is a bonding MO orbital, occupied with two electrons. This MO is not very deep in energy at -0.58753 below the relative 0 energy of the molecule and so will have quite a large effect on bonding.
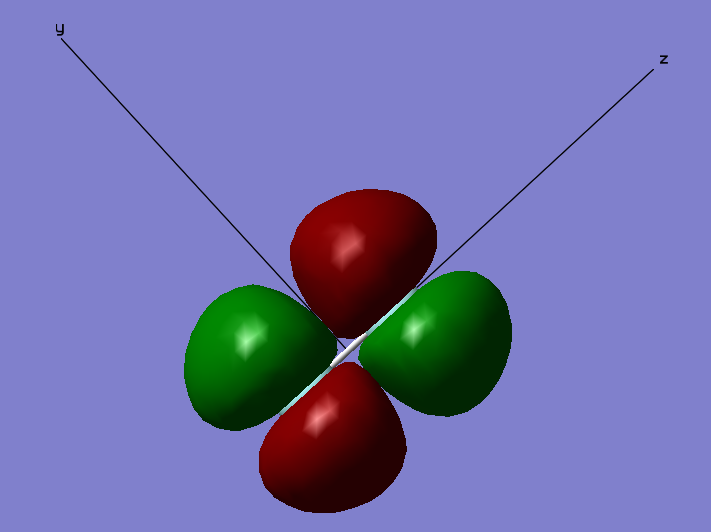
2 π u Bonding Orbital
The Cartesian Axis shown aids in the description of the MO. The orbitals described so far have been sigma orbitals. This is a π orbital. Sigma orbitals have no nodes along the bonding axis. Conversely this π orbital has a node along the bonding axis (shown with the Cartesian axis as the z axis). This is an occupied bonding orbital formed through the combination of two 2px orbitals that lie orthogonal to the bonding axis. This orbital is not very deep in energy at a relative -0.52332 which lies close to the relative 0 energy and so this MO has a strong effect on bonding. There is an additional orbital that of degenerate energy which is formed as a result of the constructive overlap of two 2py orbitals. This degenerate orbital lies orthogonal to the orbital shown in the diagram as another π orbital and exhibits the same shape as this orbital.
1 π g (2px) antibonding orbital
This is the HOMO of the F2 molecule. This is an antibonding orbital occupied by 2 electrons (Note, as before, there is an additional degenerate antibonding orbital occupied by two electrons along the orthogonal y axis exhibiting the same shape). This antibonding orbital is formed as a result of the destructive overlap of the 2px orbitals orthogonal to the bonding (z) axis. This orbital is found in the HOMO/LUMO energy region. As this orbital is located in the HOMO/LUMO region it has a large effect on bonding.
2pz σ u Antibonding Orbital
This is the LUMO in the MO of F2. This is the 2 σ antibonding orbital and is not occupied by any electrons. It is in the HOMO/LUMO region of energy and is formed as a result of the destructive overlap of two 2pz orbitals. As a result of being located in the HOMO/LUMO energy region, this orbital has a large effect on bonding. As the LUMO, if it was to be occupied by electrons, the strong σ bond primarily holding the two F atoms together would break. Therefore this orbital is very important in determining bonding. As a result, this orbital can be considered to have a large destabilising effect on the bonding of the molecule.
Independent section - H2SiO
Summary Information
What is the molecule? H2SiO
What is the calculation method? RB3LYP
What is the base set? 6-31G(d,p)
What is the final energy E(RB3lYP) in atomic units (au)? -365.90001403
What is the RMS gradient (au)?0.00000941
What is the point group of your molecule? Cs
What is the optimised SiH bond distance( Å )? 1.48652
What is the optimised SiO bond distance( Å )? 1.53172
What is the optimised OSiH bond angle( degrees )? 124.156
Item Table
Item Value Threshold Converged? Maximum Force 0.000023 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000023 0.001800 YES RMS Displacement 0.000017 0.001200 YES
Vibrational Analysis
All frequencies here are positive showing that the molecule has been fully optimised.
Charge Distribution
Hydrogen: 0.090
Silicone: 0.681
Oxygen: -0.502
This charge distribution is as expected for this molecule. Oxygen is the most electronegative atom therefore will attract electrons most strongly. Therefore this is expected to have the most negative value.