Rep:MOD:2VHW10

Introduction

Bonding varies widely across inorganic chemistry with various approximations in use for the understanding and prediction of bonding in computational and experimental chemistry including LCAO, MO and Lewis theory. The aim of this project is to use MO theory (and MO diagrams) to calculate and visualise the molecular orbitals on a range of inorganic compounds, and to use the data collected from the calculations to predict properties of the molecules under investigation such as charge distribution, NBOs and the energy of the stable state (calculated by optimization and frequency calculations).

Optimisation of Molecules

BH3

To optimise the BH3 molecule the B-H bonds of the molecule were set to 1.5Å before running a B3LYP 3-21G optimisation on the mocule to give: Optimised BH3 Molecule using B3LYP, the complete set of data (.log file) can be found here.

The following data was then extracted from this optimised model using the inquiry button in Gaussview:

B-H Bond Length: 1.19 Å

H-B-H Bond Angle: 120.0°

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy	-26.46226338 a.u.
RMS Gradient Norm	0.00020672 a.u.
Dipole Moment	0.0000D
Point Group	D3H
Job Time	42.0 s

Conformation of Optimisation Completion

The optimisation can be confirmed by checking that the job (calculation) has truly convereged - since YES appears for each item and a stationary point has been found (i.e. as the gradient is tending towards zero) the job is considered converged and the optimisation complete.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.

Analysing Optimisation

The RMS Gradient Norm gives the gradient of the optimised molecule - as it tends towards zero the molecule is taken to be optimised (at a value of less then 0.001). The gradient shows the change in energy as each step of the optimisation is completed, as such when the gradient tends towards zero it is showing that the change in energy in each optimisation step is close to zero, therefore it can be taken that the molecule is at the minimum energy once the gradient is zero (i.e. further optimisation steps will not minimise the energy further). Hence, it is expected that the final structure observed as part of the optimisation plot will have the most negative energy (the minimum) and the smallest gradient, this is taken to be the minimum of the potential energy surface, and the equilibrium (optimised) structure of the molecule under calculation. When the gradient goes to zero the stable structure of the molecule is observed.

6-31G (p,d) Basis Set

The first optimisation using the 3-21G optimised file was then re-optimised using a higher level basis set, 6-31G(d,p) (the symmetry was switched off to give the right minimum energy) to give the following optimised molecule: Optimised BH3 Molecule using B3LYP 6-31G (d,p) Basis Set, the complete data files are found here.

The following data was then taken from Gaussview using the inquiry function:

B-H Bond Length: 1.19Å

H-B-H Bond Angle 120.0°

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-26.61532374 a.u.
RMS Gradient Norm	0.00000236 a.u.
Dipole Moment	0.0000D
Point Group	CS
Job Time	23.0 s

The CS conformation confirms the no symmetry function of the calculation has been correctly used.

Conformation of Optimisation Completion

         Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000020     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-1.312911D-10
 Optimization completed.
    -- Stationary point found.

Differences Observed Using Different Basis Sets

Energy of Optimisation

3-21G Basis Set: -26.46226338 a.u.

6-31G(d,p) Basis Set: -26.61532374 a.u.

The energies of the two calcualtions depends on the level of the basis set. Whilst in atomic units the energy difference does not seem large, only varying in the decimal places, in real terms the energy difference is very large. Upon conversion to more farmiliar chemical terms -

3-21G Basis Set: 69476.6725 kJ/mol

6-31G(d,p) Basis Set: 69878.53248 kJ/mol

This shows an energy difference of approximatly 400 kJ/mol confirming that there are large differences between the two calculations when varying basis sets - and therefore no comparison can be made between molecules analysed with different methods or basis sets.

TlBr3

The optimisation of this molecule used a restricted symmetry (where the calculation constrained the point group to D3h very tighyly (0.0001)) and gave the following optimised molecule: Optimised TlBr3 Molecule using B3LYP LanL2DZ (Set Symmetry).

The calculation was run on the HPC service with the basis set LanL2DZ basis set and the results published to D-Space here: Completed Optimisation of TlBr3 in D-Space

The following data was then retrived from the results of the optimisation:

Tl-Br Bond Length: 2.65 Å

Br-Tl-Br Bond Angle: 120.0°

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Final Energy	-91.21812851 a.u.
RMS Gradient Norm	0.00000090 a.u.
Dipole Moment	0.0000D
Point Group	D3H
Job Time	18.5 s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084083D-11
 Optimization completed.
    -- Stationary point found.

Comparison of Computational and Measured Values

The bond length of the Tl-Br bonds in TlBr3 can be compared to those found in literature to estimate the validity of the optimisations calculated - however since the bond lengths in references are calculated in either solid state or solution (the liquid phase) there will be differences compared to the calculations carried out using basis sets in the gas phase. The literature value reported for the length of the Tl-Br bond as between 2.49-2.52 A depending on the aqueous hydration state of the molecule. ^[1] This is of a similar magnitude to my calculation of 2.65 A - since some variation in length is expected due to the use of approximate wave functions (basis sets) and the use of iterative methods. However, the values calculated using Gaussian are of a similar magnitude to those calculated in literature using higher level basis sets and other methods - suggesting that my calculation is accurate if not precise.

BBr3

This molecule was optimised using a mixture of basis-sets and pseudo potentials due to the mixture of both light and heavy atoms in the molecule. The 6-31G(d,p) basis set was used on the Boron atom whilst the Bromine atoms in the molecule used the LanL2DZ the pseudo-potential basis set and pseudo-potential to give the results below: Optimised BBr3 Molecule using B3LYP 6-31G (p,d) Basis Set & Pseudo Potential. The calculation was run with symmetry in place (as attempts at calculation with the key word string nosymm gave rise to C2V symmetry - however this may be due to a problem in the programme as discussed below in the frequency analysis section, since all data values for the calculations are equivalent with or without symmetry). Full data for the calculation can be found here.

The resulting optimised structure showed the following values:

B-Br Bond Length: 1.93 Å

Br-B-Br Bond Angle: 120.0 °

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	Gen
Final Energy	-64.43645296 a.u.
RMS Gradient Norm	0.00000382 a.u.
Dipole Moment	0.0000D
Point Group	D3H
Job Time	24.0 s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027544D-10
 Optimization completed.
    -- Stationary point found.

Analysis of Calcualted Data

Comparing Bond Lengths for Different Molecules

Molecule	Bond Length Å
BH3	1.19
BBr3	1.93
TlBr3	2.65

The length of the bonds depends on both atoms in the bond - with variations in size, electronegativity and the overlap of atomic orbitals affecting the strength and therfore the length of the bond. Where the two atoms have good orbital overlap, and orbitals are of similar size and not diffiuse bonds will be strong and bond lengths shorter - these factors make it possible to explain the differences in bond length for molecules that are isostructural. BH3 is the shortest strongest bond whilst TlBr3 is the longest bond, and therefore the weakest, BBr3 has intermediate bond length and as such strength.

Changes in ligand for the same central atom give rise to differences in bond length due to a change in electronegativity (the polarisation of the bond) and differences in orbital size and diffusivity: BH3 has a shorter bond length and a stronger bond then BBr3 due to the more effecient orbital overlap of the small denser orbitals of the atoms involved in bonding. This is due to the overlap of the 1s, 2p orbitals on Boron and 1s orbitals on Hydrogen which is more efficient then the overlap between the 1s, 2p orbitals on Boron and the 4s, 3d and 4p orbitals on the Bromine atom, due to the similar sizes of Boron and Hydrogen orbitals, whilst Bromine orbitals will be much larger and more diffuse then those of the Boron atom leading to poor overlap. The larger difference in electronegativity between Boron and Bromine, as opposed to Boron and Hydrogen, will also give rise to weaker bonds as orbitals that are very different in energy show less stabilisation when combined then those closer in energy. Whilst Hydrogen and Bromine both donate the same number of electrons to Boron - 1 electron per atom to give 6 electrons in the valence shell - they show differences in properties and reactivity due to the Hydrogen electron being donated into the bonding system from an s orbital where as the electron donated from Bromine is donated from the p orbitals; since s orbitals are spherically symmetric this leads to a different type of overlap to that of the p orbitals which have nodes. There is also the possibility for Bromine to donate some electron density from a lone pair into the empty p orbital orthogonal to the plane on the Boron to alleviate the electron deficiency of the compound, this will strengthen the bond however this is unlikely to overcome the poor overlap observed in bonding between a small 2nd row element and a larger, more diffuse atom further down the periodic table. Therefore, the B-H bond is stronger then the B-Br bond due to several affects.

How changing the central element effects the bond length of these isostructural (trigonal planar) compounds can be observed by comparing the bond lengths of BBr3 and TlBr3 - where TlBr3 has a longer, weaker bond then BBr3. Since Boron and Thallium are in the same period of the periodic table (13) they have similar physical properties - with similar modes of bonding and the same number of valence electrons - in both of the complexes used in calculations the central atoms are electron deficient with only 6 electrons in their valence shells, although this may be to a small extent alleviated by backbonding from Bromine lone pairs. The back bonding however will have different strength depending on the central atom due to similar factors as those that apply to ordinary sigma single bonding. In this case Thallium has much larger and more diffuse orbitals then Boron, this gives rise to poor overlap with the Bromine atoms then that observed between Bromine and Boron (where Boron has much less diffuse orbitals since the electrons are more tightly bound around the nucleus in lower energy shells). Furthermore, since Thallium and Bromine are both large elements with many electrons in several different shells they are further apart in space without breaking certain physical principle. However, it would be expected for Thallium and Bromine to show greater stabilisation upon overlap of atomic orbitals due to more similar electronegativies and therefore orbital energies then those of Boron and Bromine (where Bromine is much more electronegative then Boron). However, since orbital diffusivity effects and size of orbitals have a greater effect on orbital overlap and therefore bond strength: BBr3 has a stronger, longer bond then TlBr3.

Bonds in Gaussview

The concept of bonding is somewhat subjective, but in simple terms a bond is an area of high electron density between two atoms that gives rise to a lower energy state then if the electrons were only associated with a single atom. The sharing of electrons between two atoms however implies that the electron is constrained to be held between two atoms, where as in reality (from quantum mechanics) electrons can be found at much larger distances from the molecule, in molecular orbitals (orbitals formed by combination of atomic orbitals) that depending on symmetry operations (defined from mathematical theory) can have different shapes and sizes. Bond strengths and lengths depend on the size of the orbitals, the overlap between orbitals on different atoms, the difference in electronegtivity between the atoms (and therefore the energy difference between orbtials) and orbital type (e.g. s, p, d, f - which effect symmetry). Therefore, the definition of bonding required for any instance is determined by the complexity of the problem and the level of understanding required. Furthermore, different types of bonding - ionic, covalent, metallic - call for different theories for the definition of a bond, hence the wide variation in inorganic chemistry in particular.

In the case of computational analysis, since the programmes used are capable of solving complex functions, required by quantum mechanics, via iterative methods it is possible to use the probability density concept of the bond. Therefore, the bond is essentially an area of high electron density, where the probability of the electron(s) being found is a somewhat arbitrary definition within the computational programme - usually somewhere between 75-95%.

In some structures Gaussview does not draw the bonds between atoms, however this does not mean that there are no bonds present. Since a bond is a subjective concept, in simple terms where the electrons are most likely to be found (as discussed above), at a certain distance the probability falls to zero. This probability falls to zero since for any two given atoms when the 'bond' reaches a certain length there would be no effective orbital overlap between the two atoms and therefore no stabilisation gained from bond formation. Since, the optimisation calculation is used to find the minimum energy of a molecule - the stable state - there will be points in the optimisation where the distance at which the atoms are placed is larger then the some what arbitrary (defined by the calculation programme) maximum length for a bond - therefore in the Gaussview programme no bonds may be drawn. This does not necessarily mean that there is no overlap, or attraction between two atoms - however there is a set level at which the calculation assumes no bond is present and this may be observed in some steps of the optimisation.

Frequency & Vibrational Analysis

Vibrational analysis is carried out on optimised molecules to confirm that the minimum structure is being observed. The frequency analysis is the second derivative of the potential energy surface calculated during the optimisation step: if the frequencies are positive then a minimum has been found but if one of them (or more) is postive then a transition step has been located. If this is the case then the optimisation has not been completed since a minimum energy point has not been found. The frequency analysis has further use as IR and Raman spectroscopy modes can be detailed from the calculation.

The same method and basis set must be used for optimisation and frequency calculations on the same molecule due to different levels of basis sets giving rise to different structures and energys. Since frquency calculations are essentially proving that the optimisation calculation was compelted correctly use of a different basis set level will give rise to a different energy which would be a different structure - and not valid for use in further calculations. The frequency calculation is the second derivate of the calculation in the optimisation - if a different basis set was used a different answer would be achieved.

BH3

The frequency calculations for this molecule were completed using the original optimisation file (above), using the 6-31G(d,p) to give the structure shown here: Frequency Calculation of the BH3 Molecule using the 6-31G(d,p) Basis Set, the complete data file is found here.

The following data about the molecule was taken:

B-H Bond Length: 1.19 Å

H-B-H Bond Angle 112.0°

This data is the same as that calculated from the optimisation, therefore suggesting the same structure has been calculated and therefore the calculation was succesful.

Calculation Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-26.61532374 a.u.
RMS Gradient Norm	0.00000237 a.u.
Dipole Moment	0.0000D
Point Group	C2V
Job Time	19.0 s

Although the point group in the calculations summary shows C2V as the point group, since the previous optimisation shows CS (due to the nosymm tag in the calculation) it would be expected that the nosymm tag was used in the frequency calculation and the point group would be CS. Looking through the frequencies of the output file no symmetry has been assigned (shown below) and therefore the molecule can be discussed in terms of CS (no symmetry) - it is likely due to a default or bug in the programme.

        1                      2                      3
                     A                      A                      A
 Frequencies --  1162.9785              1213.1756              1213.2363
 Red. masses --     1.2531                 1.1072                 1.1072
 Frc consts  --     0.9986                 0.9601                 0.9602
 IR Inten    --    92.5514                14.0572                14.0608

Also, since the minimised energy observed is the same as for the optimised molecule, this would also suggest the same structure is observed as before, showing the calculation has been completed along with the data below.

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000020     0.001800     YES
 RMS     Displacement     0.000009     0.001200     YES
 Predicted change in Energy=-1.329322D-10
 Optimization completed.
    -- Stationary point found.

Frequencies Analysis

The Low Frequencies calculated are the six frequencies that are not included in the 3N-6 vibrational frequencies (the normal modes of a non-linear molecule) of the molecule - these are the motions of the centre of mass of the molecule and therefore are very small in comparison to the first vibrational mode. The low frequencies are 3 translational modes of the molecule (i.e. in the x, y and z directions) whilst the other 3 are three angles that define the direction of the molecular axis^[2], as internal rotational displacements. The remaining 3N-6 modes are the normal modes expected from a non-linear molecule, although not all are observable due to symmetry constraints and changes in dipole moment.

Low frequencies ---  -18.6669   -0.0007   -0.0001    0.0008   12.5167   12.5631
 Low frequencies --- 1162.9785 1213.1756 1213.2363

The frequencies of the vibrations of the molecules are shown below, symmetry groups were analysed by re-running the calculation with the symmetry imposed on the molecule (tight symmetry D3h) so that the vibrations calculated had a defined symmetry group. Since all vibrations are positive the minimum energy has been found and the optimisation confirmed complete.

Vibrational Frequencies Summary
#	Form of Vibration	Frequency	Intensity	Symmetry D3h Point Group
1	All Hydrogen atoms move in and out of the plane of the molecule in a concerted manner (wagging), whilst the Boron atom moves in and out of the plane in the opposing direction	1163	93	A2"
2	Two Hydrogen atoms move in symmetric strech motion in the plane of the molecule, while the third hydrogen atom and the boron move together to linearly opposed this motion	1213	14	E'
3	Boron atom does not move, but rocking motion of boron atoms - with 1 atom opposing the motion of movement of the others (antisymmetric)	1213	14	E'
4	The totally symmetric stretch of the molecule - the boron atom remains stationary whilst the hydrogen atoms move in a concerted motion in and out (in the plane of the molecule)	2582	0	A1' Totally Symmetric
5	One Hydrogen atom remains stationary whilst the two other atoms move back and forth in a assymetric strecch (opposite directions), there is small movement in the stationary Hydrogen - Boron bond	2715	126	E'
6	Symmetric stretch of two hydrogens, with the assymetric stretch of another (i.e. opposing the direction of motion), the boron atom remains stationary	2715	126	E'

IR Spectrum

The IR spectrum was then calculated from the frequency calculation -

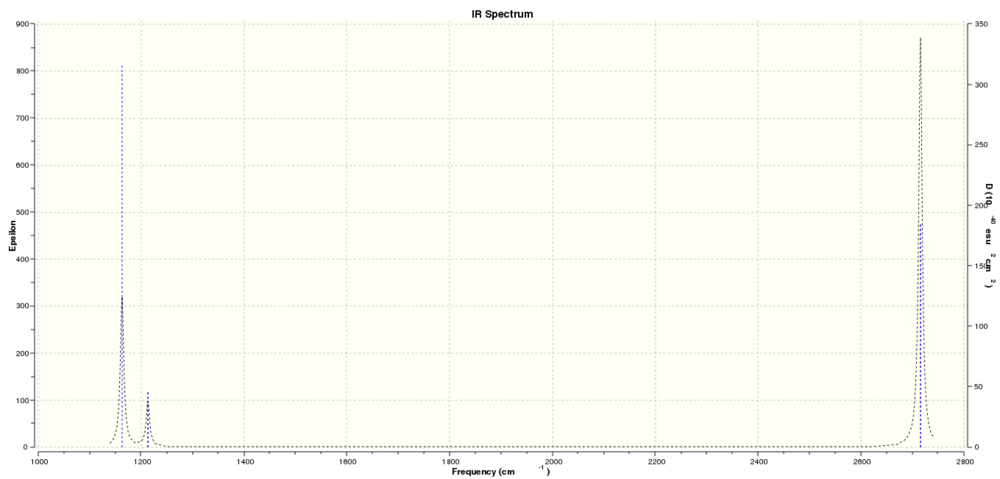
There are only 3 peaks in this spectrum despite the 6 stretches expected due to the requirements for a given vibration to interact with an electric field (i.e. the Infrared radiation using for this form of spectroscopy). The requirement that the vibration gives a change in dipole means thats symmetric stretches are not observed in the spectrum, furthermore degenerate motions only appear as one peak in the spectra since the energy required for such a vibration is equal for both modes.

TlBr3

The frequency calculations for this molecule were completed using the original optimisation file (above), using the LanL2DZ pseudo-potential to give the structure shown here: Frequency Calculation of the TlBr3 Molecule using the LANL2DZ Pseudo Potential.

The calculation was run on the HPC service with the basis set LanL2DZ basis set and the results published to D-Space here: Completed Frequency Calculation of TlBr3 in D-Space.

The following data about the molecule was taken:

Tl-Br Bond Length: 2.65 Å

Br-Tl-Br Bond Angle 119.0°

The data observed, within an expected error, is the same as the data calculated for only the optimisation, suggesting the same structure has been observed as would be expected.

Calculation Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Final Energy	-91.21812851 a.u.
RMS Gradient Norm	0.00000088 a.u.
Dipole Moment	0.0000D
Point Group	D3H
Job Time	16.7 s

Since the same final energy is observed for the frequency calculation as for the original optimisation this shows the success of the calculation - as it proves that the structure observed is the same as after optimisation.

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-5.660840D-11
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The low frequencies show the completion of the calculation to minimise the vibrations - therefore suggesting the optimisation is complete. The first 6 low frequencies (in the top line) show the 6 vibrational modes available in the 3N-6 vibrations for any molecule.

Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9362    3.9362
 Low frequencies ---   46.4289   46.4292   52.1449

The lowest 'real' normal mode is a degenerate (in plane) sicssoring motion at 46.43 cm^-1.

Vibrational Frequencies Summary
#	Form of Vibration	Frequency	Intensity	Symmetry D3h Point Group
1	Scissoring (symmetric) action of 2 Br atoms in plane of molecule, the third Br atom and B atom move in the opposing direction to the other atoms in the plane of the molecule	46	4	E'
2	The central Tl atom remains stationary whilst 2 of the Bromine atoms wag in the plane of the molecule in one direction whilst the other opposes this motion (assymetric wag)	46	4	E'
3	All Br atoms move out of the plane of the molecule concertedly in the opposing direction to the B atom (symmetric twist)	52	6	A2"
4	All Br atoms move in and out (in the plane of the molecule) together in a concerted motion, the B atom remains stationary (symmetric stretch)	165	0	A1' Totally Symmetric
5	A single Br atom remains in position with a assymetric stretching motion for the other two bromines, leading to some small motion of the Tl atom in the opposing direction (assymetric stretch) of motion	211	25	E'
6	Two Bromine atoms move concertedly in a stretching motion, the third bromine atom stretches in the opposing direction with little movement of the central atom in space (assymetric stretch)	211	25	E'

IR Spectrum

Using the optimised frequency file the IR spectrum of the molecule TlBr3 was calculated:

There are less then six peaks in the IR spectrum despite there being six vibrations because degenerate vibrations appear as a single peak in the spectrum. Also, the totally symmetric vibration does not appear since it has no change in dipole and therefore is not observed under IR spectroscopy. Therefore due to the 2 degenerate stretches, and 1 symmetric stretch only 3 peaks appear in the spectrum.

Comparison of IR frequencies in Isostructrual Compounds

Vibrational Frequencies
#	BH3	TlBr3
1	1163 A2"	46 E'
2	1213 E'	46 E'
3	1213 E'	52 A2"
4	2582 A'1	165 A1'
5	2751 E'	211 E'
6	2751 E'	211 E'

The large difference in the frequencies values between BH3 and TlBr3 indicates the large difference in mass between the two compounds, indicated by the reduced mass of the molecule, and also the difference in the strength of the bonds within the molecule. The vibrational frequency ( $ω$ ) of a molecule is quantum mechanically defined as -

ω = \sqrt{\frac{k}{4 π^{2} c^{2} μ}}

where $μ$ is the reduced mass of the molecule, k is the spring constant (i.e. related to the strength of the bond) and c is the speed of light. Therefore, since the frequency is proportional to the square root of the spring constant and inversely proportional to the square root of the reduced mass it is possible to understand the variation in calculated vibrational frequencies between the two molecules. Since the reduced mass of TlBr3 is so much larger then that of BH3 (a much lighter molecule) it would be expected for TlBr3 to have lower frequency vibrations due to the inverse proportionality expressed in the equation above. Furthermore, the length of the bond (determined by its strength) is longer in TlBr3 then in BH3 and as such the weaker bond gives rise to a lower vibrational frequencies due to the proportionality between bond strength (the spring constant) and vibrational frequency. The larger difference in the value of frequencies between the two molecules is due to the large difference in weight and bond length.

There has been a reordering of modes between the two molecules, however there are an equal number of modes as expected due to the isostructural nature of the molecules. In BH3 the A2" mode is the lower energy mode, whereas in TlBr3 the same mode is higher in energy then the E' mode. All other modes remain the same. The spectra are therefore similar in that they both show three peaks in a similar pattern - with 2 peaks close together at a lower frequency and one more intense peak (larger change in dipole moment)at a higher frequency, although there is more overlap of peaks in the TlBr3 spectrum where as in BH3 the peaks are well defined.In both spectra two vibrational modes like close together (A2" and E') whilst the other two modes (A1' and E') also lie close together but with a higher energy. This is due to the lower energy modes being bending modes whilst the higher energy modes are all stretching modes.

Molecular Orbitals

Population Analysis of BH3

This energy calculation was run on the HPC service with the basis set 6-31G(d,p) (with no symmetry constraints), defining full nbos and a full population analysis (pop=full) and the results published to D-Space here: Completed Optimisation of BH3 in D-Space. The following structure is obtained: Energy Calculation of BH3 Molecule using B3LYP 6-31G (d,p) Basis Set.

The following data about the molecule was obtained after the calculation:

B-H Bond Length: 1.19 Å

H-B-H Bond Angle 120.0 °

Calculation Summary
File Type	.fch
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-26.61532374 a.u.
RMS Gradient Norm	0.00000000 a.u.
Dipole Moment	0.0000D

BH3 Molecular Orbital Diagram

THe MO diagram of trigonal planar D3h BH3 is shown below (with LCAOs for each energy level) and the calculated MOs shown -

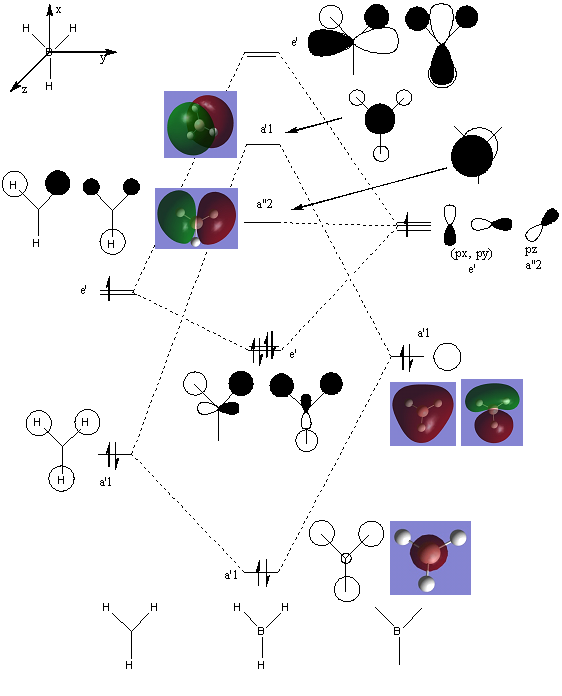
Real vs. Calculated MO Comparisons

The major differences between the real and LCAO MOs is the addition of one extra MO in the real MO set - the 1st MO shows bonding only on the Boron atom and this therefore shifts all the other orbitals which match the LCAO orbitals very well up by one energy level. Therefore, the total symmetric bonding orbital that is the lowest energy orbital under the LCAO approximation becomes the second lowest energy orbital under calclualtion. Also, under the calculation method there are 8 electrons in the molecule (as opposed to 6 via LCAO methods), which gives rise to the LUMO being an energy level higher then that of the LCAO method (orbital 5 under calculation but only degenerate a"2 orbital 4 under LACO). These differences define the energy levels of the molecule however in general the orbital images created under calculation match realtivly well for example the e' LCAO approximations are almost iddentical (once the orbtial has been spread across the entire molecule) to those calcualted in theory (orbitals 3 &4). It should be noted that under LCAO orbitals are drawn but do not necessarily show overlap across the whole molecule (as a visulation technique) but can be considered to be delocalised over the molecule with the phases observed much like the calculated molecular orbitals.

These differences and similarities suggest that whilst qualitative MO theory is useful for visualisation of orbitals - since orbitals are similar when compared - that they ordering of orbitals and the number of electrons does not hold across the two methods (the addition of 2 electrons shifts the HOMO-LUMO band and necessarily the orbitals). Therefore, whilst the theory is useful the level of accuracy as the size of molecules increases and variations in electronic effects come into play is not as high as calculation methods.

NBOs

Optimisation of NH3

NH3 was optimised using the 6-31G(d,p) basis set (since the molecule is small - this higher level set can be used immediately) using the B3LYP method and the symmetry switched off to give the right minimum energy. The final optimised molecule is shown here: Optimised NH3 Molecule using B3LYP 6-31G (d,p) Basis Set, and the full data file can be found here.

The following data was then taken from Gaussview using the inquiry function:

B-H Bond Length: 1.02 Å

H-B-H Bond Angle 105.7°

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-56.55776856 a.u.
RMS Gradient Norm	0.00000885 a.u.
Dipole Moment	1.8464D
Point Group	C1*
Job Time	1min 15.0 s

Molecule run with nosymm tag hence the return of a point group with very little symmetry (E only) - the expected point group is C3v

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629728D-09
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The frequency calculations for this molecule were completed using the original optimisation file (above), using the 6-31G(d,p) basis set to give the structure shown here: Frequency Calculation of the NH3 Molecule using the 6-31G(d,p) basis set, and the data can be found here.

The following data about the molecule was taken:

N-H Bond Length: 1.02 Å

H-N-H Bond Angle 105.7°

Since bond lengths and angles are similar this suggests that the same structure of the molecule has been calculated under the frequency analaysis as the optimisation. This is also confirmed by the same (to 6 d.p) minimum energy calculated, shown below:

Calculation Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-56.55776856 a.u.
RMS Gradient Norm	0.00000878 a.u.
Dipole Moment	1.8464D
Point Group	C1*
Job Time	22.0 s

Molecule run with nosymm tag - expected point group is C3v

The structure is considered optimised due to the conformation below, and the similarity of the energy between the frequency calculation and the optimisation in the previous step. The fact these energies are the same (within error) shows that the same structure has been derived in both cases and so optimisation is achieved.

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000021     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000077     0.001800     YES
 RMS     Displacement     0.000039     0.001200     YES
 Predicted change in Energy=-1.592773D-09
 Optimization completed.
    -- Stationary point found.

Vibrations

Low Frequencies Analysis

Low frequencies ---  -30.8045    0.0010    0.0014    0.0016   20.2188   28.2150
 Low frequencies --- 1089.5530 1694.1235 1694.1861

The vibrational frequencies are detailed below, there are no negative frequencies showing the frequency calculation has been successful (i.e. a minimum in energy has been found).

Vibrational Frequencies Summary
#	Frequency	Intensity
1	1090	1
2	1694	1
3	1694	1
4	3461	1
5	3589	1
6	3589	1

Population Analysis

This energy calculation was run on the HPC service with the basis set 6-31G(d,p) (with no symmetry), defining full nbos and a full population analysis (pop=full)to obtain the following structure: Energy Calculation of NH3 Molecule using B3LYP 6-31G (d,p) Basis Set, the population analysis file can be found here.

The following data about the molecule was obtained after the calculation:

N-H Bond Length: 1.02 Å

H-N-H Bond Angle 105.7 °

Calculation Summary
File Type	.chk
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-56.55776856 a.u.
RMS Gradient Norm	0.00000000 a.u.
Dipole Moment	1.8464D

NBO & Charge Distribution Analysis

The charge distribution of the NH3 molecule uses the data from the population analysis (energy calculation). The charge limits (NBO) are between -1.125 and 1.125, giving rise to the following visualisation (green is highly positive and red is highly negative).

The specific NBO charges for the molecule are:

Nitrogen NBO: -1.125

Hydrogen NBO: 0.375

This shows, as expected, that the nitrogen has a high charge density due to its electronegative and as such withdraws any electron density from the hydrogen's leaving them with a lower charge density.

Ammonia Borane

Ammonia Borane is an acid-base complex, with a dative bond formed using the lone pair from nitrogen into the empty p orbital of the electron deficient Boron atom. The energy of the dative bond can be calculated using association energies, as calculated below.

When completing an optimisation on a product molecule to be used to calculate a reaction energy (for a dative bond in this case) the calculation must be completed at the same level as for the reactants. In this case this means a two step optimisation, since BH3NH3 is too large a molecule - with 8 atoms to run only the higher basis set (6-31G), below are presented the two optimisation steps, run with no symmetry as for the reactant molecules.

B3LYP 3-21G Optimisation

The first step of the optimisation process used a drawn BH3NH3 molecule (bond stretched to 2A) and the basis set 3-21G to give: Optimised NH3BH3 Molecule using B3LYP 3-21G.

The calculation was run on the HPC service with the basis set 3-21G basis set and the results published to D-Space here: Completed Optimisation of Borane Ammonia in D-Space

The following data was then extracted from this optimised model using the inquiry button in Gaussview:

B-N Bond Length: 1.69 Å

H-B-H Bond Angle: 113.6 °

H-N-H Bond Angle: 109.4°

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy	-82.76661873 a.u.
RMS Gradient Norm	0.00005907 a.u.
Dipole Moment	5.8416D
Point Group	C1*
Job Time	37.4 s

Run with a no symmetry constraint (nosymm), therefore expect the molecule to show no symmetry as observed since C1 only has the identy (E) function (as opposed to C3v the point group of the molecule).

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000102     0.000450     YES
 RMS     Force            0.000053     0.000300     YES
 Maximum Displacement     0.000958     0.001800     YES
 RMS     Displacement     0.000461     0.001200     YES
 Predicted change in Energy=-2.349289D-07
 Optimization completed.
    -- Stationary point found.

B3LYP 6-31G Optimisation

The second step of the optimisation uses the higher level basis set 6-31G and gives: Optimised NH3BH3 Molecule using B3LYP 6-31G(d,p).

The calculation was run on the HPC service with the 6-31G basis set and B3LYP method and the results published to D-Space here: Completed Optimisation of Borane Ammonia in D-Space

The following data was collected from this optimised model using the inquiry button in Gaussview:

B-N Bond Length: 1.67 Å

H-B-H Bond Angle: 113.9 °

H-N-H Bond Angle: 107.9 °

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31g(d,p)
Final Energy	-82.22469027 a.u.
RMS Gradient Norm	0.00005968 a.u.
Dipole Moment	5.56216D
Point Group	C1*
Job Time	45.1 s

Run with a no symmetry constraint (nosymm) - with the same point group as the previous optimisation.

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000143     0.000450     YES
 RMS     Force            0.000039     0.000300     YES
 Maximum Displacement     0.001034     0.001800     YES
 RMS     Displacement     0.000227     0.001200     YES
 Predicted change in Energy=-1.172705D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The frequency calculations for this molecule were done with the original optimisation file (above), using the 6-31G(d,p) basis set to give the structure shown here: Frequency Calculation of the NH3BH3 Molecule using the 6-31G(d,p) basis set.

The calculation was run on the HPC service with the 6-21G basis set and the results published to D-Space here: Completed Optimisation of Borane Ammonia in D-Space

The following data about the molecule was taken:

B-N Bond Length: 1.66866 Å

H-B-H Bond Angle: 113.906 °

H-N-H Bond Angle: 107.862 °

These bond lengths seem to be within that expected for computational analysis as observed in literature, with BN bond lengths of approximately 1.655Å ^[3] which fits with the value calculated above.

Calculation Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-83.22469027 a.u.
RMS Gradient Norm	0.000005986 a.u.
Dipole Moment	5.5621D
Point Group	C1*
Job Time	53.9 s

Molecule run with nosymm tag - expected point group is C3v

The structure is considered to have remained optimised after the frequency analysis since the energies of the molecules match after the calculations have been run - the data shown below (and the low frequencies) confirm the calculations have been completed.

Conformation of Optimisation Completion

 Item               Value     Threshold  Converged?
 Maximum Force            0.000272     0.000450     YES
 RMS     Force            0.000060     0.000300     YES
 Maximum Displacement     0.001505     0.001800     YES
 RMS     Displacement     0.000384     0.001200     YES
 Predicted change in Energy=-2.255468D-07
 Optimization completed.
    -- Stationary point found.

Vibrations

Low Frequencies Analysis

Low frequencies ---   -9.3346   -0.0008   -0.0005    0.0009   19.4090   19.4507
 Low frequencies ---  263.2666  631.1809  638.5364

The vibrational frequencies are shown below, note that there are no negative frequencies (all other information about vibrations is available in the .log file contained in the D-space above)and as such the calculation is considered to have converged (reached a minimum energy).

Vibrational Frequencies Summary
#	Frequency	Intensity
1	263	1
2	631	5
3	639	1
4	639	1
5	1069	1
6	1069	1

Association Energy Calculation

The association energy for the combination of one molecule of NH3 with one molecule of BH3 to get the product NH3BH3 is calculated below:

E(NH3)= -56.55776856 a.u.

E(BH3)= -26.61532374 a.u.

E(NH3BH3)= -83.22469027 a.u.

ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]= [-83.22469027]-[(-56.55776856)+(-26.61532374)]= (-83.22469027)-(-83.1730923)= -0.05159797 a.u.

ΔE (Dissociation Energy) = -0.05159797 a.u. = -135.4704702 kJ/mol (±10 kJ/mol)

This value matches relativly well with the literature value, calculated using other computational methods and higher level basis sets, of 27.6 kcal/mol (115.43 kJ/mol)^[4], there is a relativly large difference but the calculations are of the same order of magnitude and of the magnitude expected for a bond dissociation (for a relativly week bond) which suggests within the error of the low level basis sets this value is realtivly accurate.

Accuracy

The error in the energy of the molecule for the methods used is ~ 10 kJ/mol which is approximatly 0.0038088 a.u. (1 a.u. (hartree) = 2625.50 kJ/mol).

Values are recorded within the accuracy constraints for these calculations (due to methods and calculation errors) as reported here.

Investigating Aromaticity

Benzene is the stereo-typical conjugated molecule against which the resonance energies of most conjugated organic molecules are compared. This is due to the higher resonance energy observed in the system - the highest for any single ring system - attributed to both the ring size and optimal overlap of the orbitals in this system.

In this project benzene and its isoelectronic (replacement of a C-H unit with fragments) analogues will be investigating, with considerations such as its conformers, vibrations and MOs.

The four molecules under study are:

Benzene-C₆H₆
BorataBenzene - C₅H₅BH^-
Pyridinium - C₅H₅NH⁺
Borazine - [BNH]₃

They are all isoelectronic with 42 electrons, benzene and borazine are uncharged whilst boratabenzene anion carries a -1 charge and the pyridinium cation a +1 charge.

Benzene as a Reference Molecule

Optimisation

Due to the size of the molecule (12 atoms) under study two levels of optimisation will be used (3-21G followed by 6-31G under the B3LYP Method) - this will reduce the amount of computational time since geometry and bond lengths will be optimised at a lower level before the higher level calculation refines them. All calculations are run with the nosymm (no symmetry) tag - this will mean that in all summary data no symmetry (no point group) will be observed.

3-21G Optimisation

The optimisation of this molecule used no symmetry and gave the following optimised structure: Optimised C6H6 Molecule using B3LYP 3-21G (NoSymm). The calculation was run on the HPC service with the 321-G basis set (B3LYP Method) and the results published to D-Space here: Completed Optimisation of Benzene in D-Space

The following data was then retrieved from the results of the optimisation:

C-C Bond Length: 1.40 Å

C-C-C Bond Angle: 120.0°

This is the value expected for a bond in benzene - some where between a single and double bond (due to the conjguation in the molecule), where all bond lengths and angles are the same. These values (within their error (±0.01Å)) agree with the literature values of 1.39Å^[5]. The bond angles of the molecule are in agreement with the structural hybridisation expected for the sp2 hybrid carbons. Therefore, along with the calculation summary (and the proof of convergance) below this suggests the correct (structural) minimum has been found to be further optimised in the next calculation stage.

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy	-230.97576955 a.u.
RMS Gradient Norm	0.00011167 a.u.
Dipole Moment	0.0001D
Point Group	C1
Job Time	36.5 s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000216     0.000450     YES
 RMS     Force            0.000076     0.000300     YES
 Maximum Displacement     0.000726     0.001800     YES
 RMS     Displacement     0.000267     0.001200     YES
 Predicted change in Energy=-4.465157D-07
 Optimization completed.
    -- Stationary point found.

6-31G Optimisation

The second optimisation of this molecule used no symmetry (as before so that the correct molecular minimum is reached) but a higher basis set under the same method and gave the following optimised molecule: Optimised C6H6 Molecule(NoSymm).The calculation was run on the HPC service with the 631-G(d,p) basis set (B3LYP Method) and the results published to D-Space here: Completed Optimisation of Benzene in D-Space

The following data was retrived upon optimisation:

C-C Bond Length: 1.40 Å

C-C-C Bond Angle: 120.0°

Since, within error, this is the same as above the same structure found in the optimisation step, with the same geometry (D3h - despite the nosymm tag) the optimisation has been succesful and suggests that any further optimisation would be redundant. A small change in the minimum energy (below) is observed but this is expected due to the change in basis set, and therefore since all other factors show convergance, the molecule is considered optimised.

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-232.25821232 a.u.
RMS Gradient Norm	0.00003385 a.u.
Dipole Moment	0.0000D
Point Group	C1
Job Time	1 min 18.1s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000071     0.000450     YES
 RMS     Force            0.000019     0.000300     YES
 Maximum Displacement     0.000124     0.001800     YES
 RMS     Displacement     0.000049     0.001200     YES
 Predicted change in Energy=-2.213309D-08
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The frequency calculations for this molecule were completed using the second optimisation level (above), using the 6-31G(d,p) bassis set to give the structure shown here: Frequency Calculation of the C6H6 Molecule using the 6-31G(d,p) Basis Set. The calculation was run on the HPC service and the results published to D-Space here: Completed Frequency Calculation of Benzene in D-Space.

The following data about the molecule was taken using Gaussview's inquiry function:

C-C Bond Length: 1.40 Å

C-C-C Bond Angle 120.0°

Calculation Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-232.25821232a.u.
RMS Gradient Norm	0.00003395 a.u.
Dipole Moment	0.0000D
Point Group	C1
Job Time	4 Minutes 26.6s

The energy being equivalent to the energy of optimisation (apart from the decimal places - errors due to the itterative calculation method) shows that the same minimum structure has been reached and therefore the same geometry observed in the optimisation and frequency calcualtions. This, means that the calculation has converged (along with that stated below), since the frequency calcualtion is a conformation that the optimisation found the required minimum and not a transition state, and as such the vibrational values outputted from the calcualtion can be taken as valid.

Conformation of Optimisation Completion

Force            0.000082     0.000450     YES
 RMS     Force            0.000034     0.000300     YES
 Maximum Displacement     0.000123     0.001800     YES
 RMS     Displacement     0.000064     0.001200     YES
 Predicted change in Energy=-2.555736D-08
 Optimization completed.
    -- Stationary point found.

Frequencies Analysis

Low frequencies ---   -5.1651   -0.0005    0.0003    0.0007   13.0464   16.7439
 Low frequencies ---  414.1400  414.9609  621.1691

The vibrational 'low' frequencies shown above have no negativevalues and as such the frequency calculation is considered succesful and the minimum energy state of the molecule has been obtained (the freqeuncy calculation is the second derivative of the energy/optimisation curve and as such a negative value implies a transition as opposed to a low energy potential energy state).

Energy Calculations: MOs & NBOs

Population Analysis

The energy calculation for benzene was run on the HPC service with the basis set 6-31G(d,p) (with no symmetry - as used in the optimisation/fequency steps), defining full nbos and a full population analysis (pop=full) to obtain the following structure: Energy Calculation of C6H6 Molecule using B3LYP 6-31G (d,p) Basis Set, published to D-Space here:Completed Energy Calculation of Benzene.

The following data about the molecule was obtained after the calculation:

C-C Bond Length: 1.40 Å

C-C-C Bond Angle 120.0°

Calculation Summary
File Type	.chk
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-232.25821219 a.u.
RMS Gradient Norm	0.00000000 a.u.
Dipole Moment	0.0000D

NBO & Charge Distribution Analysis

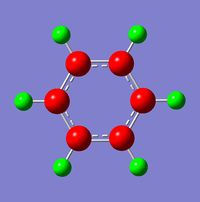
The NBO (natural bond orbital) charge distribution analysis was completed using the energy calculation from above, the charge distribution (NBO) is between -0.239 to 0.239, and detailed right.

The specific NBO charges for the molecule are:

Carbon NBO: -0.239

Hydrogen NBO: 0.239

The charge distribution across the molecule is even (as expected by the symmetry and equivalence of the molecule (D6h)) as the carbon framework has no additional electron withdrawing or donating atom to vary the charges across the molecule. The hydrogens being electron deficent and the carbon atoms having excess electron density (therefore charge) around them (a negative charge density value). The total charge density values across the molecule are zero - with the carbon atoms being equal and opposite in electron density to the carbon atom, as expected by physical constraints.

MO Diagram for Benzene

The MO diagram for the carbon framework of Benzene is shown below, with the LCAOs and the calculated MOs from Gaussian Energy Calculations, only the carbon framework orbitals were visualised and hence only carbon molecular orbitals shown in the image below:

The pi and core sigma orbtials (1s) were visualised using standard methods (where the nodes of the orbitals increase in each subsequent, higher energy orbital). The core sigma orbtials, from the 1s orbitals of the six carbon atoms, are much lower in energy then the rest of the orbitals in the molecule, and therefore show no interaction with other carbon orbitals. The rest of the sigma orbitals were interpreted from the sigma MOs calculated using the energy calculations above, and information about the equivalent linear form of benzene; Hexatriene^[6].

Aromaticity and Molecular Orbitals:

Aromaticity is defined as existing in any cyclically conjugated molecule with 4n+2 valence electrons (Huckel's rule) that gives rises to a lowering of electronic energy and stabilises the molecule^[7]. In the case of benzene there are 4n+2 electrons where n=1 (there are 6 valence electrons) and the cyclic conjugation can be inferred from the molecular orbital diagram. Only the pi orbitals are relevant in cyclic conjugation, and therefore only orbitals with pi type symmetry are considered in aromaticity. In benzene the pi type orbtials closest to the frontier orbitals are relevant and therefore orbitals 17 and 20 to 23 are taken into consideration - where all orbitals are perpendicular to the plane of the molecule. In the totally bonding pi system there are orbitals along the top and bottom faces of the molecule (of different phases) this allows the delocalisation of one electron from each carbon atom in the ring, an electron pair for each molecular orbital. Therefore, the concept of aromaticity in benzene is upheld by the molecular orbital picture, as well as by the total pi electron density shown by the concentration of pi molecular orbitals in the compound.

BorataBenzene

BorataBezene is an isoelectronic analogue of benzene, with an equal number of valence electrons, where one CH unit has been replaced with the BH^- unit to give C5H5BH^- molecule. Therefore, with an electropositive atom in the molecule the charge distribution and MOs of the compound are expected to differ from those of the symmetric (D6h) benzene molecule, they will also differ due to the broken symmetry in the molecule since the additional electropostivive boron no longer leaves all atoms in the carbon framework equivalent.

Optimisation

As for benzene two optimisation steps were used to reduce computing time, all calculations were run with no symmetry to allow the right energy minimum to be calculated during the optimisation steps. The same method is used for both optimisation steps (B3LYP) as one optimisation works off the basis of the lower basis set.

3-21G Optimsiation

The following optimised molecule was calculated: Optimised BorataBenzene(NoSymm), where the calculation was run on the HPC service with the 2-31G basis set (B3LYP Method) and the results published to D-Space here: Optimisation of BorataBenzene in D-Space

The following data was found upon optimisation:

C-C Bond Length: 1.40 Å

B-C Bond Length: 1.51 Å

C-B-C Bond Angle: 115.5°

All C-C bond lengths observed are equivalent, due to conjugation along the carbon framework, C-C-C bond angles vary due to the presence of a smaller C-B-C bond angle in the 6 membered ring compared to the perfect sp3 angles observed in benzene molecules, this is due to the variation in physical properties of the isoelectronic (B-H)^- unit. The B-C bond length is longer then that of the C-C bond length (which remains the same as in the symmetrical perfect benzene), due to the presumed poorer overlap between the carbon and boron atoms in comparison to the all carbon analogue.

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy	-217.81414730 a.u.
RMS Gradient Norm	0.00004260 a.u.
Dipole Moment	5.3731D
Point Group	C1
Job Time	1 minute 26.1s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000075     0.000450     YES
 RMS     Force            0.000021     0.000300     YES
 Maximum Displacement     0.000284     0.001800     YES
 RMS     Displacement     0.000085     0.001200     YES
 Predicted change in Energy=-4.309502D-08
 Optimization completed.
    -- Stationary point found.

6-31G Optimisation

The higher level optimisisation of the molecule was calculated: Completely Optimised BorataBenzene(NoSymm), where the calculation was run on the HPC service with the 6-31G basis set (B3LYP) and the results published to D-Space here: Completed Optimisation of BorataBenzene in D-Space

The following data was found upon optimisation:

C-C Bond Length: 1.40 Å

B-C Bond Length: 1.51 Å

C-B-C Bond Angle: 115.2°

These values are similar to those calcualted in the pre-optimisation step and along with the data provided below showing no dramatic shifts in energy, and the conformation that convergence was achieved suggests the optimisation has found the same geometry as the previous step.

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-219.0205427 a.u.
RMS Gradient Norm	0.00019098 a.u.
Dipole Moment	5.2351D
Point Group	C1
Job Time	1 minute 20.7s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000235     0.000450     YES
 RMS     Force            0.000095     0.000300     YES
 Maximum Displacement     0.001781     0.001800     YES
 RMS     Displacement     0.000516     0.001200     YES
 Predicted change in Energy=-1.136328D-06
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The frequency calculations were completed using second optimisation file (above), using the 6-31G(d,p)basis set to give the structure shown here: Frequency Calculation of the C5H5BH- Molecule using the 6-31G(d,p) Basis Set. The calculation was run on the HPC service with the basis set 6-31G(B3LYP Method) and the results published to D-Space: Completed Frequency Calculation of BorataBenzene in D-Space.

The following data about the molecule was taken:

C-C Bond Length: 1.40Å

B-C Bond Length: 1.51Å

C-B-C Bond Angle 115.2°

The values are similar to those observed above, suggesting the same structural conformational minima has been found in the correct geometry. The frequency and optimisation calculations have the same energy (within the error of the decimal point) which supports the correct geometry been found, and confirming a minimum energy value has been confirmed.

Calculation Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-219.02052427 a.u.
RMS Gradient Norm	0.000190988 a.u.
Dipole Moment	5.2351D
Point Group	C1
Job Time	4 Minutes 42.21

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000448     0.000450     YES
 RMS     Force            0.000191     0.000300     YES
 Maximum Displacement     0.002066     0.001800     NO 
 RMS     Displacement     0.000711     0.001200     YES
 Predicted change in Energy=-1.292328D-06

The Item table above does not show the file converging, however upon checking the output .log file the geometries were found to be the same as in the previous optimisation step, with the same coordinate system, the low frequencies are low (shown below - for within the basis set) and the vibrations have been assigned and are positive. The maximum displacement is only just over the threshold value allowed which also suggests a minimuym value had already been calcualted before the step commenced. Since the calculation terminated normally after an expected amount of time (compared to similar calculation runs), this suggests that the frequency has convereged and therefore a minimum geometry has been found, confirming the optimisation calculations found the minimum and therefore the calculation is considered complete and used in the next step of the calculation.

Frequencies Analysis

Low frequencies ---  -17.4249   -3.6271   -0.0008    0.0004    0.0006   10.4857
 Low frequencies ---  370.7425  404.4177  565.0814

The low frequencies are all positive, confirming a minimum has been found and all vibrations are therefore positive for the optimised conformation. Whilst the 6 internal motions have a larger value then that expected from calculations, this appears to be acceptble due to the poor level basis set in use for this calculation, and thus the low frequenceis are taken as conformation a structural minimum has been found.

Energy Calculations: MOs & NBOs

Population Analysis

The energy calculation for boratabenzne was run on the HPC service with the basis set 6-31G(d,p) (with no symmetry - as used in the optimisation/frequency steps) from the frequency file (since the apparent non-convergence should not affect the energy analysis), defining full nbos and a full population analysis (pop=full) to obtain the following structure: Energy Calculation of C5H5BH- Molecule using B3LYP 6-31G (d,p) Basis Set, published to D-Space here:Completed Energy Calculation of BorataBenzene.

The following data about the molecule was obtained after the calculation, with MOs for the molecule being discussed in comparison to Benzene later in the report:

C-B Bond Length: 1.51Å

C-C Bond Length: 1.40Å

C-B-C Bond Angle 115.2°

Calculation Summary
File Type	.chk
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-219.02052427 a.u.
RMS Gradient Norm	0.00000000 a.u.
Dipole Moment	5.2352D

NBO & Charge Distribution Analysis

The NBO (natural bond orbital) charge distribution analysis was completed using the energy calculation from above, the charge distribution (NBO) is between -0.588 to 0.588, and detailed below:

The specific NBO charges for the molecule are:

The charge distribution in BorataBenzene is no longer symmetric (compared to benzene) due to the replacement of an isoelectronic unit of CH with BH^-. The Carbon framework has a varying charge distribution due to the polarisation of the system by the electropostive Boron atom, with all hydrogens but the one bonded to the hydrogen still lacking electron density whilst the carbon atoms are still electron rich, although those closer to the Boron atom have a more negative charge distribution then those furhter round the ring. THe Boronic hydrogen is also electron rich due to its attachment to the electron positive boron atom as expected.

Pyrdinium

Pyridinium is an alternative isoelectronic analogue of benzene, with an equal number of valence electrons, where one CH unit has been replaced with the NH+ unit to give the C5H5NH+ molecule. The electronegative Nitrogen atom in the molecule is like to give rise to variation in the charge distribution and MOs of the compound from those of the symmetric (D6h) benzene molecule, they will also differ from the Boratbenzene molecule since the charge distribution is opposite and therefore the polarity of the unit is opposed to the changes observed for Boratabenzene.

Optimisation

Two levels of optimisation were carried out (B3LYP Method - 3-21G and 6-31G Basis Sets) for reasons similar to those above, mainly lowering the amount of computing time, the results are shown below:

3-21G Optimisation

An optimised molecule was calculated: Optimised Pyridinium Cation(NoSymm), the calculation was run on the HPC service with the 2-31G basis set (B3LYP Method) and the results published to D-Space: Completed Optimisation of the Pyridinium Molecule.

The following data was found upon optimisation of the molecule:

C-C Bond Length: 1.40 Å

N-C Bond Length: 1.36 Å

C-N-C Bond Angle: 122.5°

The Carbon Carbon bonds lengths are as expected from previous calculations and known literature values for Benzylic bonds, where all carbons are equivalent since they are part of a conjugate system. The bond angles for the C-C-C angle vary around the ring, due to the slightly larger bond angle for C-N-C, with smaller bond angle then that expected from the six membered ring system (with sp2 bond angles) due to slight variances in ring symmetry by the addition of the slightly larger Nitrogen atom in the ring as opposed to the carbon framework in benzene. The Carbon - Nitrogen bond length is shorter then that of the conjugated C-C bonds, and is not involved in the conjugated system according to the calculation, although upon further energy calculations this will be visualised in the MOs (confirming or denying the presence of conjugation around the entire, or part of, the ring).

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy	-247.28364284 a.u.
RMS Gradient Norm	0.00019845 a.u.
Dipole Moment	6.4129.D
Point Group	C1
Job Time	55.3s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000417     0.000450     YES
 RMS     Force            0.000134     0.000300     YES
 Maximum Displacement     0.001772     0.001800     YES
 RMS     Displacement     0.000679     0.001200     YES
 Predicted change in Energy=-1.695191D-06
 Optimization completed.
    -- Stationary point found.

6-31G Optimisation

The following optimised molecule was calculated: Optimised Pyridinium (NoSymm), where the calculation was run on the HPC service with the 6-31G basis set (B3LYP Method) and the results published to D-Space here: Completed Optimisation of Pyridinium in D-Space

The following data was found upon optimisation, with similar values of bond length and angles from the previous optimisation suggesting the geometries are the same and a minimum has been calculated:

C-C Bond Length: 1.40 Å

N-C Bond Length: 1.35Å

C-N-C Bond Angle: 123.3°

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-248.66806594 a.u.
RMS Gradient Norm	0.00004944 a.u.
Dipole Moment	6.3533D
Point Group	C1
Job Time	2 minute 25.7s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000102     0.000450     YES
 RMS     Force            0.000032     0.000300     YES
 Maximum Displacement     0.000863     0.001800     YES
 RMS     Displacement     0.000254     0.001200     YES
 Predicted change in Energy=-1.453774D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The frequency calculations were completed using second optimisation file (above), using the 6-31G(d,p)basis set to give the structure shown here: Frequency Calculation of the C5H5NH+ Molecule using the 6-31G(d,p) Basis Set. The calculation was run on the HPC service with the basis set 6-31G(B3LYP Method) and the results published to D-Space: Completed Frequency Calculation of Pyridinium Cation in D-Space.

The following data about the molecule was taken from the calculation to confirm the calculation provided the same values, and therefore the same structure as in the previous optimisation steps:

C-C Bond Length: 1.40 Å

N-C Bond Length: 1.35 Å

C-N-C Bond Angle 123.3°

Calculation Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-248.66806594 a.u.
RMS Gradient Norm	0.00004935 a.u.
Dipole Moment	6.3533D
Point Group	C1
Job Time	4 Minutes 28.5s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000133     0.000450     YES
 RMS     Force            0.000049     0.000300     YES
 Maximum Displacement     0.000976     0.001800     YES
 RMS     Displacement     0.000338     0.001200     YES
 Predicted change in Energy=-1.519824D-07
 Optimization completed.
    -- Stationary point found.

Frequencies Analysis

The low frequencies are low, with the first six being below -12 as expected, to show that the frequency calculation has found a minimum which confirms the optimisation process has been completed during the calculation, and therefore the minimum energy calculated is the global minimum, proven by all vibrational frequencies being positive (as opposed to a transition state).

 Low frequencies ---   -6.3849    0.0005    0.0006    0.0007   11.1801   13.9456
 Low frequencies ---  391.5394  404.4363  620.4576

Energy Calculations: MOs & NBOs

Population Analysis

The energy calculation for pyridinium was run on the HPC service with the basis set 6-31G(d,p) (with no symmetry), defining full nbos and a full population analysis (pop=full)to obtain the following structure: Energy Calculation of Phyridinium Molecule using B3LYP 6-31G (d,p) Basis Set, published to D-Space here:Completed Energy Calculation of Pyridinium Cation.

The following data about the molecule was obtained after the calculation, Molecular orbitals for the molecule were also calculated and are discussed below:

C-C Bond Length: 1.39 Å

C-N Bond Length: 1.35 Å

C-N-C Bond Angle 123.3 °

Calculation Summary
File Type	.chk
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-248.66806594 a.u.
RMS Gradient Norm	0.00000000 a.u.
Dipole Moment	6.3534D

NBO & Charge Distribution Analysis

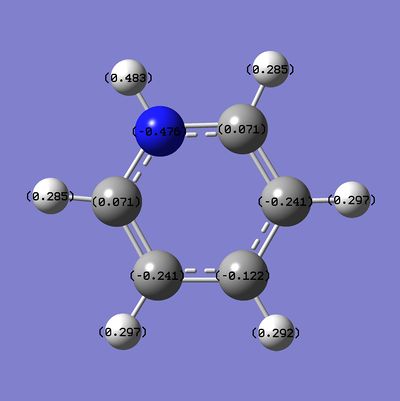
The NBO, charge distribution analysis was completed using the energy calculation run, the charge distribution (NBO) is between -0.483 to 0.483:

The specific NBO charges for the molecule are:

The charge distribution shows variation along the carbon framework due to the presence of an electronegative nitrogen atom in the ring system, with the carbon atoms closest to the nitrogen having the most positive values of charge (i.e. with the least electron density around them due to the influences of the nitrogen atom) and the framework having more negative values of charge density further from the electron withdrawing atom, since the spatial distance means that the atom has a less withdrawing effect. All Hydrogen atoms have positive charge densities, and therefore are electron deficient in comparison to the atoms they are bonded to - with the Hydrogen atom bonded directly to the Nitrogen atom bearing the highest positive charge density since most electron density is withdrawn from directly bound atoms.

Borazine

Borazine is an isoelectronic compound of Benzene, with all CH units replaced with either a BH- or NH+ unit to give a compound with the same number of electrons as Benzene, Boratabenzene and the Pyridinium cation. Since all carbon units are replaced with heteroatom units there expected to be a much larger variation in charge distribution and molecular orbitals then for the other Benzene analogues, although many of the properties of the compound are similar to Benzene - hence the compounds name as 'inorganic benzene'.

Optimisation

Two levels of optimisation were carried out for reasons similar to those discussed for the other molecules under calculation, the results are shown below for both basis sets:

3-21G Optimisation

The following optimised molecule of borazine was calculated, from the fixed double/single bond structure: Optimised Borazine(NoSymm), where the calculation was run on the HPC service with the 2-31G basis set (B3LYP Method) and the results published to D-Space: Completed Optimisation of Borazine

The following data was found upon optimisation:

B-N Bond Length: 1.45 Å

N-H Bond Length: 1.02 Å

B-H Bond Length: 1.19 Å

N-B-N Bond Angle: 117.0°

B-N-B Bond Angle: 123.0°

In the Gaussview image the conjugation in the molecule is not defined, however this is due to the programmes definition of what is and is not a bond as discussed previously. The bond lengths are as expected for a molecule of Borazine in literature (1.4355Å ^[8]), and the conjugated 'view' of the molecule is shown here. The B-N bond lengths and relative angles of the molecule are all the same suggesting a conjugated system as expected from both the isostructurality with benzene and literautre^[8], since single and double bonds would have different lengths in the molecule and give rise to different bond angles due to varying types of hybridisation.

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy	-241.35696458 a.u.
RMS Gradient Norm	0.00005874 a.u.
Dipole Moment	0.0001D
Point Group	C1
Job Time	1 minute 11.8s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000096     0.000450     YES
 RMS     Force            0.000030     0.000300     YES
 Maximum Displacement     0.000175     0.001800     YES
 RMS     Displacement     0.000067     0.001200     YES
 Predicted change in Energy=-7.625951D-08
 Optimization completed.
    -- Stationary point found.

6-31G Optimisation

The following optimised molecule was calculated: Optimised Borazine (NoSymm), where the calculation was run on the HPC service with the higher level 6-31G basis set (B3LYP Method) and the results published to D-Space here: Completed Optimisation of Borazine in D-Space

The following data was calculated under secondary optimisation:

B-N Bond Length: 1.43 Å

N-H Bond Length: 1.01 Å

B-H Bond Length: 1.19Å

N-B-N Bond Angle: 117.1°

B-N-B Bond Angle: 122.9°

Calculation Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-242.68459787 a.u.
RMS Gradient Norm	0.000114764 a.u.
Dipole Moment	0.0002D
Point Group	C1
Job Time	2 minute 13.1s

Conformation of Optimisation Completion

 Item               Value     Threshold  Converged?
 Maximum Force            0.000121     0.000450     YES
 RMS     Force            0.000052     0.000300     YES
 Maximum Displacement     0.000584     0.001800     YES
 RMS     Displacement     0.000224     0.001200     YES
 Predicted change in Energy=-4.245288D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The frequency calculations were completed using second optimisation file (above), using the 6-31G(d,p)basis set to give the structure shown here: Frequency Calculation of the [CHBH]3 Molecule using the 6-31G(d,p) Basis Set. The calculation was run on the HPC service with the basis set 6-31G(B3LYP Method) and the results published to D-Space: Completed Frequency Calculation of Borazine.

The following data about the molecule was taken, with similar results to the previous optimisation suggesting the same geometry has been reached:

B-H Bond Length: 1.19 Å

N-H Bond Length: 1.01 Å

N-B Bond Length: 1.43 Å

N-B-N Bond Angle 117.1°

B-N-B Bond Angle 122.9°

Calculation Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-248.66806594 a.u.
RMS Gradient Norm	0.00011473 a.u.
Dipole Moment	0.0002D
Point Group	C1
Job Time	4 Minutes 40.6s

Conformation of Optimisation Completion

Item               Value     Threshold  Converged?
 Maximum Force            0.000281     0.000450     YES
 RMS     Force            0.000115     0.000300     YES
 Maximum Displacement     0.000589     0.001800     YES
 RMS     Displacement     0.000277     0.001200     YES
 Predicted change in Energy=-4.266765D-07
 Optimization completed.
    -- Stationary point found.

Frequencies Analysis

The Low frequencies are low implying that a minimum energy stationary state has been found, since there are no negative frequencies (other then the 6 internal vibrations) a minimum has been found rather then a transition state.

Low frequencies ---   -9.5786   -0.0006    0.0008    0.0011    3.6915   11.3601
 Low frequencies ---  288.6077  290.5799  404.6103

Energy Calculations: MOs & NBOs

Population Analysis

The energy calculation for borazine was run on the HPC service with the basis set 6-31G(d,p) (with no symmetry), defining full nbos and a full population analysis (pop=full) to obtain the structure here: Energy Calculation of Borazine Molecule using B3LYP 6-31G (d,p) Basis Set, published to D-Space:Completed Energy Calculation of Borazine.

The following data about the molecule was obtained after the calculation, with values simialr to those from the optimisation and frequency calculation stages, showing the same geometry has been used for the calculation:

N-B Bond Length: 1.43 Å

N-H Bond Length: 1.01Å

B-H Bond Length: 1.19Å

N-B-N Bond Angle 117.1°

B-N-B Bond Angle 122.9°

Calculation Summary
File Type	.chk
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy	-242.68459787 a.u.
RMS Gradient Norm	0.00000000 a.u.
Dipole Moment	0.0002D

NBO & Charge Distribution Analysis

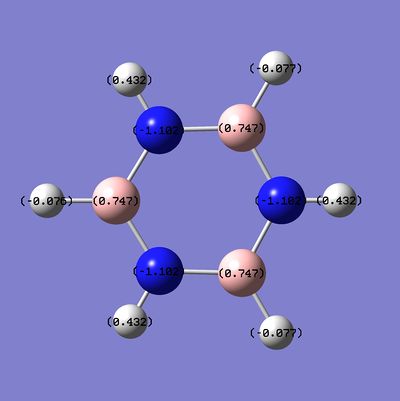
The NBO, charge distribution analysis was completed using the energy calculation run, the charge distribution (NBO) is between -1.102 to 1.102:

The specific NBO charges for the molecule are:

The framework of this structure shows symmetric charge distribution due to the inherent symmetry of the molecule with the bonding of an electronegative (Nitrogen) atom to an electropositive (Boron) gives a fluctuating charge density with high electron density around the nitrogen atoms and reduced electron density on the Boron atoms, where is has been withdrawn by the electronegative nitrogen and donated to the bonded hydrogen. Hydrogen atoms bonded to Boron have high electron density, due to the electropositive nature of the atom whilst hydrogen atoms bonded to nitrogen atoms have a lower charge density due to the withdrawing effects of the nitrogen.

Charge Distribution Analysis of Isoelectronic Structures

Benzene can be used as a reference molecule to compare isoelectronic conjugated structures too in terms of charge density and molecular orbitals - since the other compounds under study can be considered analogues where the CH unit has been replaced with a hetroatom-hydrogen unit and the molecule charge to make it isoelectronic. Therefore, it is expected that to some extent the charge density and molecular orbitals of the compounds will show similarities, with variation depending on the physical properties of the isoelectronic unit used.

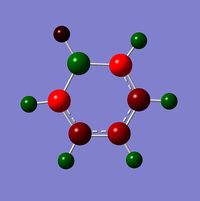
Charge Distribution

The visuals for the calculated charge distributions across the isoelectronics structures are shown below, where in all diagrams red is the negative charge density, whilst green in positive charge density - varying shades of any colour show the variation in absolute charge density, i.e. the brighter the colour the larger the magnitude of charge density. :

Charge Distribution
Benzene	Boratabenzene	Pyridinium	Borazine

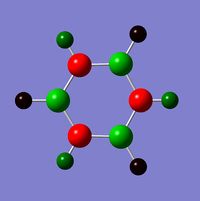
When comparing charge distributions only the variation in charge distribution (as opposed to the absolute charge distribution) can be compared, since the charge distribution numerically varies in magnitude, therefore all comparisons are qualitative (due to the varying dipoles, and therefore varying actual magnitude of charge distribution in the molecule).

Benzene: The charge distribution across benzene is symmetrical since the molecule has D6h symmetry and as such due to the aromaticity of the compound the charge (electronic) distribution would be expected to reside equally on all carbons (negative charge density - lack of electrons) and hydrogens (positive charge density - excess electrons) since all carbons and hydrogens are equivalent in the molecule. Quantitatively the charge density on the hydrogens is equal and opposite to that on the carbon, this is expected as to give a total zero charge density across the entire molecule required by physical constraints. Benzene is therefore used as a reference molecule to compare the isoelectronic molecules charge density and conjugation to, since the carbon framework is equivalent and therefore any variations are clear from the charge density diagrams. The total charge density of the molecule is zero, since the molecule is uncharged and therefore the total charge density must be zero.

BorataBenzene: The molecule shows a similar charge distribution to Benzene, with the carbon atom framework being electron rich (high charge density) whilst the hydrogen atoms attached to the framework have a low electron density. However, due to the heteroatom in the system the ring system has become polarised with the carbon atoms closest to the electropositive Boron atom having a higher charge density due to the electron donating effect of the Boron atom. The BH unit has reversed polarity to the carbon unit in benzene, with the electropositive Boron having low charge density and the hydrogen atom bonded to it therefore having a higher charge density then those bound to the carbon framework. The total charge density of the molecule, unlike the non-charged reference benzene molecule is -1, since this is the overall charge on the molecule - since the molecule is isoelectronic with Benzene and therefore must be charged due to the replacement of the CH unit with BH.

Pyridinium Cation: The pyridinium cation shows a similarly varied charge distribution to Boratabenzene, but with inverted charge. The replacement of the CH unit in benzene with a NH+ unit gives rise to a polarisation of the ring system as in Boratabenzene, however since the heteroatom is now electronegative the carbon atoms closest to the nitrogen have a lower charge density (since the electronegative nitrogen withdraws electron density from the carbon framework). Therefore, the carbon atoms furthest away from the heteroatom have the highest charge density since the effect of the electron withdrawing atom is less effective at longer distances. The hydrogen atoms in Pyridinium therefore have a higher charge density as part of the carbon framework, since the hydrogen bonded directly to the nitrogen has very low charge density due to the withdrawing nature of the nitrogen atom it is bound too. The total charge density across the molecule is -1, since the NH unit has a charge to make the compound isoelectronic with benzene and boratabenzene.

Benzene falls between Boratabenzene and Pyridinium in terms of charge distribution, due to the replacement of the CH unit with either a negatively charge BH unit or a positive NH unit which give rise to polarisation of the charge density according to the charge of the isoelectronic unit in the molecule. Therefore the charge distributions of the two isoelectronic structures is similar but of the opposite polarisation, where as the charge distribution of benzene is complete symmetric due to the innate symmetry of the carbon framework.

Borazine: The Borazine molecule is the equivalent of exchanging all of the CH Benzene units with an equal number BH- and NH+ units to give [CHBH]₃, and therefore the charge distribution would be expected to reflect the MO diagrams of both Boratabenzene and pyridinium. The charge density does not appear similar to benzene, despite the higher symmetry in the molecule compared to the other other isoelectronic structures, however the polarity of the heteroatoms in the backbone of the structure gives rise to variations in the charge density. The electronegative nitrogen atoms show a high charge density, due to their electron withdrawing nature, as they pull electron density away from the other less electronegative atoms in the compound. The hydrogen atoms bonded to the Nitrogen atom therefore have a positive charge density, as the electron density is withdrawn by the nitrogen atom as in the Pyridinium cation. The Boron atoms are electropostive and therefore have a positive charge density - with the hydrogen atoms attached to the boron having a negative charge density (as in Boratabenzene with one BH unit). Overall, much like in the Benzene molecule the compound has no charge and therefore the total charge density across the molecule is zero, as it is uncharged. Therefore, the Borazine molecule has aspects of the charge density distributions of all the isoelectronic compounds, as a systematic progression from benzene via replacing the isoelectronic CH units with heteroatom units.

Variation of MOs

The specific molecular orbitals of each compound will vary between the isoelectronic structure - due to the nature of the different isoelectronic units in each compound. There are expected to be similarities however since geometries remain similar, with only minimal distortion of the 6 membered ring, variations in charge density and varying levels of conjugation, especially since compounds are isoelectronic leading to the the frontier molecule orbitals (HOMO and LUMO) to become similar in nature. Differences however will arise due to the difference in the nature of overlap of orbitals upon the addition of heteroatoms into the system since these atoms have different energies which can change the ability of orbitals to overlap and give rise to polarisation of the bond toward one atom.

Orbital 17 - Totally Bonding Pi MO

The totally bonding pi MO in benzene is the 17th orbital (with energy -0.35997 a.u.), as known from classical LCAO theory and visualized here, where the p orbitals of the 6 carbon atoms are perpendicular to the plane of the benzene ring (all in phase) to give a conjugated pi system.

The calculated molecular orbitals (from the Gaussian energy calculations) are shown below for each isostructural compound under study -

Totally Bonding Pi Orbital
Benzene	Boratabenzene	Pyridinium	Borazine

For this totally bonding molecular orbital the MO is very similar across the set of isoelectronic molecules - due to the nature of the totally bonding combination, where all p orbitals are aligned parallel to each other with good overlap and all phases aligned. The orbitals lie only over the carbon framework to give a 'donut' of electron density typically visualised when discussing the ring currents in Benzene and other similar aromatic molecules, with opposing phases above and below the plane of the carbon framework. There are slightly variations in the size of the orbital over heteroatoms, whereas the size of the orbital on each carbon atom in benzene is the same, due to the electronegativity of the atom. Where for this bonding combination (where all p atomic orbitals are in phase) the size of the orbital on the more electronegative atoms are larger then those on the electropositive atoms, therefore in Pyridinium and Borazine the orbtials over nitrogen are slightly larger and in Boratabenzene and Borazine the orbitals over the boron atoms are slightly smaller then those in the main carbon framework - this is only slightly in evidence in these images.

Aromaticity

Benzene is an aromatic molecule and therefore it is expected that the isoelectronic analogues under investigation also show some level of aromaticity, although not with the same level of stabilisation since the addition of heteroatoms into the ring reduces stability. The totally bonding pi orbital shows aromatic characteristics and is present in all of the compound suggesting some level of aromaticity is present in all molecules, although it cannot be quantified in this way.

Orbital 22 - Lowest Unoccupied Molecular Orbital (LUMO)

The LUMO orbital of Benzene (and the isoelectronic molecules, since they all have an equal number (42) electrons) is the 22nd lowest energy orbital, visualised for benzene in terms of LCAO. The calculated molecular orbitals (via energy calculations) are shown below for each isostructural compound under study:

Charge Distribution
Benzene	Boratabenzene	Pyridinium	Borazine

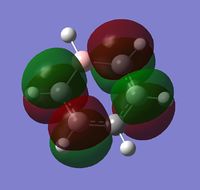The LUMO is a π^* type orbital - with orbitals (pi - out of the plane of the molecule) on four out of the six carbon atoms in the framework - with orbitals being in phase diagonally across the ring but anti-bonding on adjacent carbon atoms. The LUMO is the lowest level anti bonding orbital (i.e. the first destabilising orbital with a positive energy) and this is the concept that leads to the large stability of benzene, since all bonding orbitals are occupied and all antibonding (positive energy) orbitals are unoccupied offering no destabilisation to the molecule and ensuring its high level of stability. Due to the nature of the carbon framework (with all carbons and hydrogens being equivalent) the size of the orbitals on all atoms are equal.

Borazine and Boratabenzene show similar bonding patterns in the orbtials with pi orbitals on only four of the six carbon atoms, with a similar bonding/antibonding pattern shown to that observed in benzene, due to the similar nature of the isoelectronic molecules. However, in Borazine the framework is composed of alternating electropositive (boron) and electronegative (nitrogen) atoms which gives the orbitals different coefficients (according to quantum mechanical methods) leading to different sizes and results in larger (higher numerical coefficient) orbitals on the electropositive boron atom and smaller orbitals on the electronegative nitrogen atom. For Boratabenzene a similar effects is observed, however, since there is no orbital directly over the electropositive Boron atom the effect is slightly minimised with the carbons atoms closest to the boron atom (those with a more negative charge distribution - due to the electron donating effect of the electropositive atom on to the carbon framework) are slightly smaller in size, although this appears to be a minimal effect since the difference in charge distribution is not very large (seen above when charge distribution was discussed).

The orbital of the Pyridinium cation appears vastly different from the observed calculated MOs of the other isoelectronic compounds - with molecular orbitals across the entire molecule with one phase across the 4 central atoms in the system, and the opposite phase over the two other atoms (one begin the nitrogen, located opposite each other). As expected the orbital is larger over the Carbon (the more electropositive atom) then over nitrogen, due to quantum mechanical rules, there is also a small difference in the size of the orbtials around the carbon atoms in the framework, with the largest orbtials furthest from the electron withdrawing nitrogen in the ring.However, the 23rd orbital (which is degenerate in benzene - but not in pyridiunim (as shown right) appears very similar to the orbtials shown for this MO for the rest of the series, with orbital coefficients smallest over the nitrogen atom as expected from electronegativity considerations, however since both orbtials are unoccupied it makes little difference to the electronic properties of the molecule.

Orbital 12 - Totally Bonding in the Plane of the Molecule

The 12th energy orbital of the isostructural molecules is a bonding orbital with all p orbitals in the plane of the ring being in phase with good overlap to give one phase within the ring and an opposite phase outside the ring, as shown in the LCAO model. The calculated molecular orbitals are shown below for each isostructural compounds below:

Molecular Orbital 12
Benzene	Boratabenzene	Pyridinium	Borazine

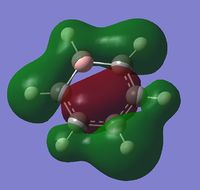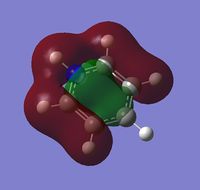In benzene the orbitals are symmetric around the ring since all carbon and hydrogen atoms in the ring are equivalent and all orbtials of the same size giving rise to good pi type overlap around the ring carbons (and sigma type overlap with the external hydrogens) - the directionality of the orbitals as shown above gives rise to a motif where the phase inside the carbon ring opposes the phase outside the ring, giving rise to a unique totally bonding orbital configuration.

The same orbitals observed for the isoelectronic analogues of benzene show a similar pattern of orbitals - with the same motif of one phase within the ring and one phase outside of the carbon framework. There are significant variations in the appearance of the orbitals for the isoelectronic compounds due to the effects of the heteroatoms on the orbital coefficients of those atoms within the ring, even propagating to effect the orbital distribution around atoms on the opposite side of the ring system. In Boratabenzene and the Pyridinium cation the orbitals observed are roughly the same as the orbitals observed in benzene however the orbital coefficients, and the charge distribution across the molecules leads to some slight variations. In Boratabenzene the largest coefficient is observed over the most electronegative atoms (since this is now a bonding orbital) - therefore the orbital size around the Boron atom is small - with no significant orbital character around the atom and a area of non conjugation around it. This leads to a differentiation between the more electronegative carbons and hydrogens and the least and therefore gives rise to a larger coefficient around the CH unit opposite to the Boron atom in the ring. Conversely, the nitrogen atom in the Pyridinium cation is the most electronegative atom and therefore is expected to have the highest orbital coefficient in the molecule, this is observed in the shift of the molecular orbitals towards the nitrogen atom in the molecule, leaving one hydrogen/carbon unit with no significant MO character.

There are significant deviations of the molecular orbital for Borazine from Benzene and the other two structures, this is likely due to the large variation in charge density around the molecule because of the nature of the electron rich and electron deficient alternating units within the molecule and the reduced symmetry. Largely the 4 central units in the molecule are of one phase and the two intervening atoms (in one case a boron and in the other a nitrogen) are of the opposite phase - however these orbitals still show the varying size coefficients expected although with reversed phase - i.e. there is very little MO density around the nitrogen atoms whilst there is a large amount of density around the Boron atom suggesting more antibonding nature in the molecular orbital (12) for Borazine, although no explanation is observed.

MO Diagrams of Isoelectronic Structures

The substitution of a CH unit in benzene for an isoelectronic XH (X=N, B) unit in another structure gives rise to variations in the full MO diagram of the compound due to differences in energy of atomic basis orbitals and deviations away from the high symmetry of the D6h benzene molecule which will break degeneracy of the orbitals. The orbital overlap (which defines the stabilisation/denationalisation of any molecular orbital is defined by the Klopman-Salem Equation -

E \propto \frac{S^{2}}{Δ E_{i}}

where E is the stabilisation/destabilisation energy, S is the overlap integral and $Δ E$ is the interaction energy (the difference in energy between orbtials).^[9]

LCAOs Contributing to MOs

The LCAOs contributing to the MOs will change largely between the series. In Benzene the atomic orbtials that contribute to the final MO structure are all equivalent since the only contributions are the six carbon atoms (1s, 2s, 2p_x, 2p_y and 2p_z) and six hydrogen atoms (1s) which gives rise to a strong overlap since all orbitals are of equal sizes and the same degenerate energies.

However, for the isoelectronic compounds the framework is no longer completely equivalent and therefore there are a different set of atomic orbtials used for the LCAO procedure. For Boratabenzene and pyridinium there are five carbons and hydrogens with equivalent orbitals as before, however where there was originally (in benzene) a sixth equivalent carbon unit the carbon has been replaced with either a Boron (Boratabenzene) or a Nitrogen (Pyridinium) with a hydrogen as part of the unit. These heteroatoms do not have the same energy as the carbon atoms (nitrogen is more electronegative and orbitals lower in energy, boron is more electropositive and orbitals higher in energy) and therefore this gives rise to a poorer overlap of the orbitals - since the carbon/heteroatom orbtials are no longer degenerate and according to the Klopman-Salem equation this gives rise to less stabilisation energy.

For Borazine all the carbon hydrogen units have been replaced with heteroatom units and therefore there are now two degenerate sets of atomic orbtials to form the molecular orbitals - with three degenerate sets of Boron orbitals, three degenerate sets of Nitrogen orbitals (and the 6 degenerate hydrogen 1s orbtials) and therefore overlap is not as optimal as for the cases with larger numbers of degenerate orbtials. Further more the energy gap (the energy of interaction) between the Boron and Nitrogen atoms is greater then for either of the atoms with carbon and therefore the orbital overlap is poor and therefore the energy of stabilisation for the orbitals will be smaller.

Energy of MOs

The energy of molecular orbitals is defined by the Klopman-Salem equation - with strong orbital overlap (a small energy gap between AOs and good overlap considering size and diffusivity of orbtials) giving rise to a large stabilisation or destabilisation energy for the new molecular orbtials formed by the linear combination of atomic orbitals (LCAO). Therefore, in benzene the stabilisation will be relatively large since overlapping orbitals are of the same energy (i.e. p_x on carbon atom 1 with p_x on carbon atom 2), and also are of good size and orientation to allow for strong overlap. However, for the other analogues there will be overlap between the heteroatom and carbon (or the two heteroatoms in the case of Borazine) which have different energies, due to variation in their electronegativities. Since there will be a difference in energy between the two sets of overlapping orbitals (i.e. p_x on Boron and p_x on carbon) the overlap stabilisation achieved will be lower. Also, the overlap between orbitals will not be as good, since the orbtials will be of varying sizes, however considering there is little difference in size between boron, carbon and nitrogen, this is not a major consideration. The largest variation in energy of molecular orbitals from the benzene reference will be Borazine, since the energy gap between the nitrogen and boron atomic orbitals will be the largest and therefore stabilisation energies will be the smallest, the same is true of orbital overlap as discussed above.

The absolute energy of the molecular orbitals of the isoelectronic series will vary dependant on the orbital overlap and AO energies, however, where these effects are particularly strong (in the orbital overlap with atoms bonded directly to the heteroatom) there may be a reordering of electronic energy levels leading to a different MO diagram, this would be particularly important in terms of changes in the frontier molecular orbitals of the compounds since it would lead to a large variation in reactivity between the analogues.

Degeneracy of MOs

The degeneracy of MOs will be due to symmetry constraints, since Benzene is a highly symmetrical molecule it is expected that there will be a large number of degenerate orbitals - since the p_x,p_y orbitals are a degenerate AO pair they will give rise to a set of degenerate molecular orbitals. However, where one of the CH units in benzene has been replaced with an isoelectronic heteroatom unit (Nitrogen or Boron) the degeneracy across the 6 orbital set (for the ring) is broken and this gives rise to a larger number of non-degenerate orbitals then observed in benzene. The degeneracy is lowered due to a change in symmetry, which gives rise to molecular orbitals not showing the same symmetry and therefore not being degenerate.

The break in degeneracy is worse for Borazine and Pyridinium since the addition of only one different atom leads to less symmetry then that of the Borazine molecule, which is more symmetric due to the replacement of all units by heteroatoms. Therefore it is expected that he highest level of degeneracy would be observed in Benzene (D6h) followed by Borazine (D3h) and the lowest level of degeneracy in BorataBenzene (C2v) and Pyridinium (C2v).

References

↑ J.Blixt, J. Glase, J. Mink., Struture of Thalliyum(III) Chloride, Bromide, and Cyanide Complexes in Aqueous Solution., J. Am. Chem. Soc., 1995, 117 (18) pp 50-89-5104., DOI:10.1021/ja00123a011
↑ Atkins & De Paula., Physical Chemistry., 9th Edition., London: OUP., 2010.,
↑ J. Demaison, J. Lievin, A.Csaszar, et.al., Equilibrium Structure and Torsional Barrier of BH3NH3., J. Phys. Chem. A., 2008, 112 pp 4477-4482., DOI:10.1002/chin.200833001
↑ C. Zirz, R. Ahlrichs., Theoretical Computation of the Binding Energy of BH3NH3, a difficult case., J. Chem. Physics., 1981, 75, pp 4980., DOI:10.1063/1.441886
↑ J. Trotter., Bond Lengths in Benzene Derivatives: Hybridisation or Resonance., Tetrahedron., 1960, 8, pp 13-22., DOI:10.1016/S0040-4020(01)93325-3
↑ Jorgensen, Salem., The Organic Chemist's Book of Orbitals.,New York: Academic Press., 1973.,
↑ Keeler, Wothers., Chemical Sturcture and Reactivity: An integrated approach., London: OUP., 2008.,
↑ ^8.0 ^8.1 W. Harshbarger, G. Lee, et. al., The Structure of Borazine., Inorg. Chem., 1969, 8 (8), pp 1683-1689., DOI:10.1021/ic50078a023
↑ A. Spivey., (2012) An Introduction to Stereoelectronics., [Lecture] Imperial College London, Department of Chemistry (Lecture 1)

[TlBr3_Bond_Length-1] J.Blixt, J. Glase, J. Mink., Struture of Thalliyum(III) Chloride, Bromide, and Cyanide Complexes in Aqueous Solution., J. Am. Chem. Soc., 1995, 117 (18) pp 50-89-5104., DOI:10.1021/ja00123a011

[Low_Frequencies-2] Atkins & De Paula., Physical Chemistry., 9th Edition., London: OUP., 2010.,

[NH3BH3_Bond_Length-3] J. Demaison, J. Lievin, A.Csaszar, et.al., Equilibrium Structure and Torsional Barrier of BH3NH3., J. Phys. Chem. A., 2008, 112 pp 4477-4482., DOI:10.1002/chin.200833001

[NH3BH3_Bond_Dissociation-4] C. Zirz, R. Ahlrichs., Theoretical Computation of the Binding Energy of BH3NH3, a difficult case., J. Chem. Physics., 1981, 75, pp 4980., DOI:10.1063/1.441886

[Benzene_Bond_Length-5] J. Trotter., Bond Lengths in Benzene Derivatives: Hybridisation or Resonance., Tetrahedron., 1960, 8, pp 13-22., DOI:10.1016/S0040-4020(01)93325-3

[MO_Reference-6] Jorgensen, Salem., The Organic Chemist's Book of Orbitals.,New York: Academic Press., 1973.,

[Aromaticity-7] Keeler, Wothers., Chemical Sturcture and Reactivity: An integrated approach., London: OUP., 2008.,

[Borazine_Bond_Length-8] 8.0 ^8.1 W. Harshbarger, G. Lee, et. al., The Structure of Borazine., Inorg. Chem., 1969, 8 (8), pp 1683-1689., DOI:10.1021/ic50078a023

[Klopman-Salem-9] A. Spivey., (2012) An Introduction to Stereoelectronics., [Lecture] Imperial College London, Department of Chemistry (Lecture 1)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]