Introduction

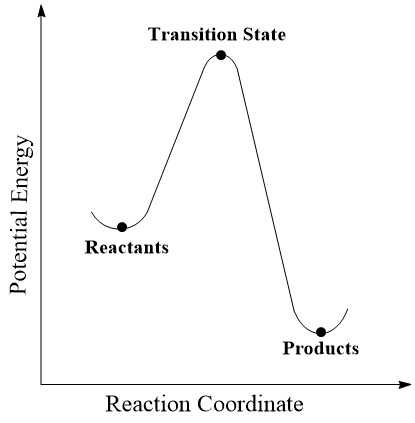
The aim of this experiement was to find and optimise the transition state structures of a number of different Diels-Alder reactions. The transition state is the structure with the highest energy point along a reaction coordinate, as can be seen in Figure 1, with the molecule needing enough energy to reach this point for the reaction to proceed. However the reaction is not just controlled by one reaction coordinate as is shown here, but will have many degrees of freedom. By using multiple reaction coordinates a multi-dimensional potential energy surface can be created.

Figure 1. Potential Energy Profile diagram along one reaction coordinate

A stationary point on the PES is the point at which all of the forces vanish, and every component of the gradient is zero. This is shown be equation 1. The values of q are the reaction coordinate, and 3N-6 is the number of normal modes of the system, with N being the number of atoms.^[1]

$\frac{\partial E (q)}{\partial q_{α}} = 0 w h e r e α = 1, 2 . . . (3 N - 6)$

The stationary point includes both the minima and the maxima of the potential energy surface. There are many local minima on a multi-dimensional surface which are at the lowest energy point in that region of the PES, with the global minima being the one with the lowest energy overall, where there is the greatest stability. The transition state is at the maxima, so in order to distinguish this, the second order derivatives must be found. These give the eigenvalues for a 3N-6 x 3N-6 matrix, known as the Hessian. A transition state is the stationary point with a single negative Hessian eigenvalue, which can be found after diagonalising the Hessian matrix. This allows the transtion state to be distinguished from the reactant and product wells, for which all diagonal components of the Hessian are positive. The lowest energy path bewtween two minima is the intrinsic reaction coordinate, and the transition state is the maxima along this path. While most of the molecules will follow the IRC, those with enough energy may have alternate pathways. Knowing the structure and energy of the transition state enables the kinetics and thermodynamics of the system to be investigated, as well as an orbital analysis.^[2]

Gaussian was used in order to calculate the position and energy of the transition state. Two types of calculation were used - the semi-emperical method PM6, to generate faster but more approximate results, and the Density Functional Theory (DFT) method B3LYP,with the 6-31g(d) basis set, to generate more accurate results, but needing a greater amount of time. The semi-empirical method is a simplified version of the Hartree-Fock method, where assumptions allow the use of experimental data for thermochemistry and molecular geometries, with DFT results being used where this is lacking. The PM6 methods uses a greater variety of types of references data than previous versions, which create 'rules' that are used for the optimisation of parameters.^[3] The B3LYP is a hybrid functional, which combines both DFT and the Hartree-Fock theory, from which the exact exchange energy can be used.^[4]

There were three methods that were used to find the transition state. The first method simply involved guessing the structure of the transition state and optimising, however while this method is fast, it is also unreliable and requires previous knowledge of the transition state, in order for the structure to be close enough for the optimisation to be successful.The second methods involves guessing the structure of the transition state, then freezing the bonds at an appropriate distance before optimising as in method 1. This method is fast and more reliable than method 1, however it does still require knowledge of the transition state. Method 3 is the most reliable, and does not require as much knowledge on the transition state as the previous methods as it involves starting from the reactant or product, altering the bond length, then using method 2 to find the transition state. However this method is longer and more involved, and is also difficult if the products or reactants do not resemble the transition state. Method 2 was used for exercises 1 and 2, while excercise 3 and the electrocyclic reaction used method 3.

Nf710 (talk) 18:40, 16 April 2018 (BST) Good understanding of the Hessian Diagonalisation, it would have been ice is you could have added some equations to back up this discussion; and some more details of the quantum mechanics would also have been good. However you have shown some further research to understand the computational methods used.

Exercise 1

(Fv611 (talk) Very good job in this whole section!)

This exercise involved a Diels-Alder Reaction between ethene and butadiene. The transition state was optimised using a PM6 calculation, with the reactants and product also optimised at this level. An MO diagram was constructed and compared to the MOs visualised for both the transition state and reactants. The bond distances of the carbon atoms were compared along the reaction coordinate from the reactants to the products, and the reaction path vibration was visualised.

MO diagram

The MO diagram for the formation of the transition state between ethene and butadiene can be seen in Figure 3. The energies of the reactant orbitals were obtained from a single point energy calculation of the reactants from the IRC, to ensure they were in same reference framework and could be compared. This shows that the LUMO and HOMO of ethene have the highest and lowest energies respectively, with the LUMO of the dienophile having a higher energy than that of the diene. The ethene LUMO is asymmetric while the butadiene LUMO is symmetric. Therefore while these two orbitals are closest in energy they are symmetry forbidden, as the integral that results from the interaction of two orbitals is only non-zero if they are of the same symmetry (symmetric with symmetric and asymmetric with asymmetric), resulting in the LUMO of ethene overlapping with the asymmetric HOMO of butadiene, producing asymmetric orbitals of the transition state. This gives an out of phase interaction of the orbitals giving the LUMO + 1, and an in phase interaction giving the HOMO-1 The LUMO+1 formed from this interaction is lower in energy that the LUMO of ethene, while the HOMO-1 is higher in energy than the HOMO of butadiene, decreasing the energy gap between them from that expected of cyclohexadiene. This is due to the fact that MO diagram is for a transition state, rather than for the product of the reaction, therefore the bonds have not fully formed. As the transition state is at the highest energy of the reaction coordinate, the orbitals are also at the highest energy, and are destabilised. The HOMO of ethene and LUMO of butadiene interact to form the HOMO (an in phase interaction) and LUMO (an out of phase interaction) of the transition state. As both are symmetric this is a symmetry allowed interaction, forming symmetric orbitals. As before, these orbitals are destabilised compared to those of the product. This reaction is a normal Diels-Alder reaction, as the HOMO of the dienophile is lower in energy than that of the diene, by a value of 0.038 Ha. These orbitals can be visualised from the PM6 calculations, and can be seen in Figure 4.

Figure 4. Molecular orbitals of the reactants and transition state

Reactant MOs

Ethene HOMO

Ethene LUMO

Butadiene HOMO

Butadiene LUMO

Transition state MOs

HOMO - 1

HOMO

LUMO

LUMO + 1

From Figure 4, the symmetry of the orbitals can be seen clearly, with the HOMO and LUMO of the transition state being symmetrical, and the HOMO-1 and LUMO+1 being asymmetrical.

Bond Distances

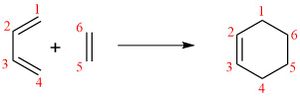
Table 1 shows the bond lengths of the carbon-carbon bonds in the reactants, transition state and product. The numbers of the carbons correspond to those seen on the reaction scheme in Figure 5.

**Table 1. Bond lengths in the reactants, transition state and product**
	Bond Length (Å)
Bond Position	Ethene	Butadiene	Transition State	Cyclohexadiene
C1-C2	—	1.335	1.380	1.501
C2-C3	—	1.468	1.411	1.337
C3-C4	—	1.335	1.380	1.501
C4-C5	—	—	2.115	1.537
C5-C6	1.327	—	1.382	1.535
C6-C1	—	—	2.115	1.537

As can be seen in table 1, the C5-C6 bond is shortest in ethene and longest in cyclohexadiene, increasing from 1.327 Å, to 1.535 Å. The same occurs with the C1-C2 and C3-C4 bonds, increasing from 1.335 Å in butadiene to 1.501 Å, with the transition state bond being in between the two. This is due to the change from a π bond to a σ bond. This can be seen by a comparison with the average length of C=C bond (1.34 Å), which is similar to those in the reactants, and the average length of a C-C bond (1.54 Å). The C1-C2 and C3-C4 bonds are slightly shorter than this value, which is due to the fact that they are adjacent to the double bond in the product. The opposite occurs with the C2-C3 bond, which decreases from 1.468 Å in butadiene to 1.337 Å in cyclohexadiene, as this is changing from a σ bond to a π bond. While the bond in the product is similar to that of an average double bond, in butadiene it is noticeably shorter than the average single bond. This is because both the carbons are sp², as it is adjacent to two π bonds. In the transition state, these bonds are closer in length to the bonds in the reactants than the bonds in the product, suggesting that the transition state is more similar to the reactants than the product, and is therefore an early transition state. The van der Waals radius of the carbon atom is 1.70 Å^[5], meaning that two carbon atoms within a distance of 3.4 Å will have van der Waals interactions between them. The σ bonds formed in this reaction (C4-C5 and C6-C1) have a bond length of 2.115 Å, showing that there are van der Waals interactions between them, however the bonds have not yet formed, as they are outside twice the covalent radius of the carbon atoms, which is 0.76 Å^[6]. In the product, the length has decreased to 1.537 Å, as is expected for a C-C σ bond.

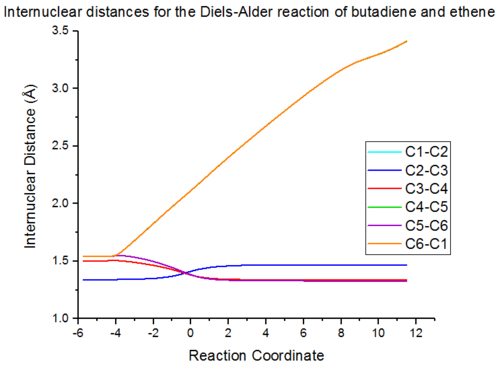
Figure 6 shows the change in bond distances throughout the reaction, obtained from the IRC. This shows the change from the product to the reactants, therefore the forwards reaction runs from left to right. Viewing the graph this way, it can be seen that the two bonds formed start at a high 'bond length' as there is no interaction between them, then as the reaction progresses the distance between them decreases, until the bond is formed. The C5-C6 bond has the same bond length as the C3-C4 bond, however increases by a greater amount and having the same bond length as the C6-C1 and C4-5 bonds. From the graph it can also been that there a point along the reaction coordinate at which all of the bonds apart from those being formed have the same bond length, which is in between that of a single and double bond.

Reaction path Vibration

Figure 7. Reaction path vibration

The vibration that corresponds to the reaction path at the transition state can be seen in Figure 7. This vibration is an the imaginary frequecy of 948i cm^-1. This vibration shows that the Diels-Alder reaction between ethene and butadiene is a concerted process, with synchronous formation of the two bonds. Further evidence can be of this can be seen in table 1, as the bonds formed are equal in length.

Exercise 2

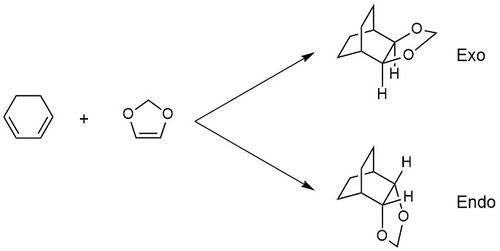
This exercise involved a Diels Alder Reaction between cyclohexadiene and 1,3-dioxole. The transition state was first optimised using a PM6 calculation, and then further optimised at the B3LYP/631-G(d). The reactants and products were also optimised at this level. This reaction has both an endo and an exo product, as can be seen in Figure 9. The MO diagram for each of these reactions was constructed and the two compared. The reaction barriers and energies were also looked at for each of the reactions.

MO Diagrams

(Fv611 (talk) Nice MO diagrams. Well done!)

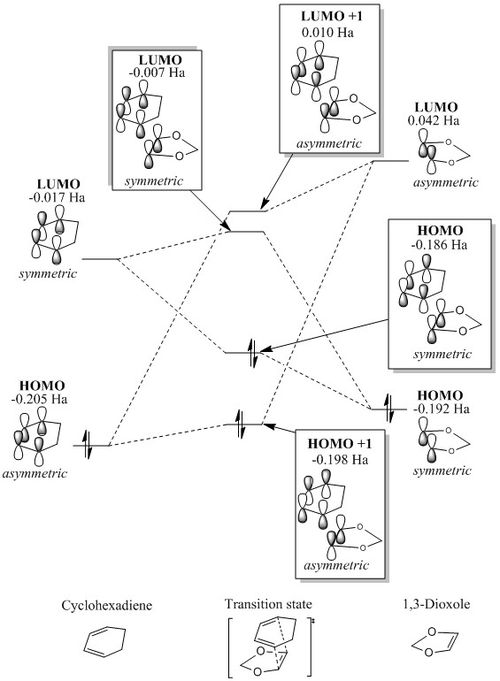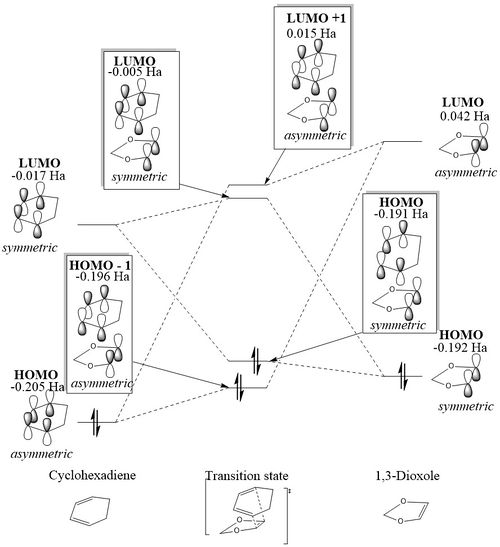
Figure 9 and 10 shows that in both the endo and the exo reaction, the LUMO of the dienophile (1,3-dioxole) has a higher energy than that of the diene (cyclobutadiene) as in the previous reaction. However in this reaction, the HOMO of the dieneophile is at a higher energy than that of the diene, unlike the reaction in exercise 1, showing that this reaction is an inverse electron demand Diels-Alder reaction. This is due to the electron-donating oxygens present in 1,3-dioxole, resulting in the species being electron rich, rather than having the electron-poor dienophile as there would be in a normal electron demand Diels-Alder reaction. For both the endo and the exo reaction the same orbitals overlap, (and the ordering of the orbitals is the same) with the asymmetric orbitals of the HOMO of cyclohexadiene and the LUMO of 1,3-dioxole overlapping to form the LUMO + 1 and the HOMO -1 of the transition state, and the HOMO of 1,3-dioxole and the LUMO of cyclohexadiene overlapping to form the HOMO and LUMO of the transition state. This also shows an inverse demand Diels-Alder, as in a normal Diels-Alder reaction, it is the LUMO of the dienophile and the HOMO of the diene which form the HOMO and LUMO orbitals of the product. The energies of the orbitals in each of the transition states is different, with the HOMO-1, LUMO+1 and LUMO of the endo transition state being higher in energy, and therefore destabilised relative to those of the exo , and the HOMO being lower in energy, as it is stabilised. The HOMO of the exo transition state is 0.005 Ha (or 13.13 kJmol^-1) higher in energy. This creates a larger energy gap between the HOMO and LUMO in the endo transition state.

Table 2. Single point energies for the endo and exo HOMO and LUMO
		MO Energy (Ha)
		Endo	Exo
HOMO	1,3-dioxole	-0.317	-0.322
HOMO	Cyclohexadiene	-0.321	-0.322
LUMO	1,3-dioxole	0.032	0.030
LUMO	Cyclohexadiene	0.023	0.021

In order for the energies of the reactant orbitals to be quantitively assessed, a single point energy calculation was run for the endo and the exo reaction, with the results shown in Table 2. From this it can be seen that while there is no difference in the energy of the HOMO of each of the reactants in the exo reactions (to 3 d.p), the endo reaction shows that the HOMO of the dienophile is lower in energy by 0.004 Ha (10.5 kJmol^-1)

Figure 11. shows the visualisation of the endo and exo transition state orbitals. From these the orientation of the 1,3-dioxole in the endo relative to the exo can be clearly seen, as well as the symmetry of each of the orbitals.

Figure 11. Transition state MOs for the endo and exo reaction

Endo Transition State MOs

HOMO - 1

HOMO

LUMO

LUMO + 1

Exo Transition state MOs

HOMO - 1

HOMO

LUMO

LUMO + 1

Secondary Orbital Interactions

The reason for the lower energy of the HOMO of the endo transition state relative to the exo can be seen in the secondary orbital interactions between the p orbitals of the cyclohexadiene and the p orbitals on the oxygens of the 1,3-dioxole. The endo transition state places these in the correct position for overlap between them, therefore stabilising the transition state and lowering its energy, however as the exo transition state has the oxygens on the opposite side, there is no opporunity for interaction between these orbitals, and therefore no stabilisation. Another reason for the lower energy of the endo transition state is due to steric hindrance that occurs in the exo product, as the 1,3-dioxole is positioned up towards the carbon bridge, while in the endo product, it points down away from the carbon bridge, and therefore avoids this destabilising steric interaction.

Figure 12. Secondary orbital interactions of the transition state HOMO orbital

HOMO

Energies

The energies of the reactants, transistion states and products were obtained from the B3LYP optimised structures, and converted from Hartrees to kJmol^-1.These vaules can be seen in table 3. From this, the activation energies and reaction energies were calculated and an energy profile diagram was created to clearly illustrate these values (Figure 12).

Table 3. Energies of the reactants, transition states and product, with the activation and reaction energies calculated
	Energy (kJmol^-1)
Reaction type	1,3-dioxole	Cyclohexadiene	Reactant total	Transition State	Activation Energy	Product	Reaction Energy
Endo	-701187.38	-612593.15	-1313780.53	-1313622.06	158.47	-1313849.27	-68.75
Exo	-701187.38	-612593.15	-1313780.53	-1313614.22	168.27	-1313845.68	-65.15

From the reaction energies it can be seen that both the exo and the endo reactions are exothermic, and are therfore thermodynamically favoured, however the reaction energy is greater for the endo product, showing that this is the preferred thermodynamic product as it is more stable than the exo product. The activation energy of the endo reaction is smaller than that of the exo, showing that less energy is needed to reach the endo transition state, therefore it will be formed faster than the exo transition state, meaning that the endo reaction is also kinetically preferred. This is due to the stabilisation of the endo transition state compared to that of the exo, as was seen previously.

Nf710 (talk) 18:47, 16 April 2018 (BST) Good section, you have done the single point energy analysis very well and have proved the electron demand. Your energies are correct and you have come to the correct conclusions. Also your jmols of the SOO are very well presented.

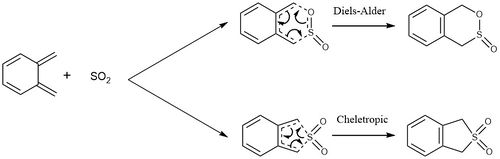
Exercise 3

In this exercise, the reactions between xylylene and SO₂ was investigated. As before there is a Diels-Alder reaction, which can proceed in an endo or an exo reaction, however there is also a cheletropic reaction which can occure, and this can be seen in the reaction scheme in Figure 13. There is also an alternate Diels-Alder reaction which can occur with the diene inside the 6-membered ring. The reaction coordinate for these reactions were investigated, and the activation energies and reaction energies were compared.

Visualisation of the reaction coordinate

The reaction coordinate of each reaction type was visualised using the IRC at the PM6 level, and these are shown in Figure 14. The IRC of the exo Diels-Alder reaction shows the oxygen not involved in the formation of the ring orientated away from xylylene, while in the endo reaction is is orientated towards it. In both of the Diels-Alder reactions it can be seen that the C-O bond forms before the C-S bond, therefore there is asynchronous bond formation, however in the cheletropic reaction, both of the C-S bonds form simultaneously, showing synchronous bond formation. In all of the reactions the 6-membered ring forms an aromatic system with 6π electrons as SO₂ starts to bond to xylylene. This is what drives the reaction forward, giving stability to the products and causes xylylene to be highly unstable.

(GaussView uses a distance cutoff to decide when to draw a visual bond, but you can't use this to decide when a bond is formed Tam10 (talk) 13:35, 4 April 2018 (BST))

Figure 14. Animations of the IRCs for the endo and exo Diels-Alder reactions and the cheletropic reaction
Endo Diels-Alder	Exo Diels-Alder	Cheletropic

Energies

The energies of the reactants, transition state and product was obtained from the PM6 calculation for the endo, exo and cheletropic reaction. The activation energies and reaction energies were calculated, and these are shown in table 5. As in exercise 2, an energy profile digram was created to visualise these results easily (figure 15).

Table 4. Energies of the reactants, transition states and products for the reactions between xylylene and SO₂
	Energy (kJmol^-1)
Reaction type	SO₂	Xylylene	Reactant total	Transition State	Activation Energy	Product	Reaction Energy
Exo	-311.38	466.43	154.94	241.75	86.81	56.32	-98.61
Endo				237.77	82.83	56.98	-97.97
Cheletropic				260.09	105.15	0.00	-154.94

From the activation energies it can be seen that the cheletropic reaction has the largest energy barrier to the reaction, so is the least kinetically preferred. This is due to the formation of the strained 5-membered ring in comparison to the 6-membered ring formed in the Diels-Alder transition state, which has a lower degree of strain. The activation of the endo and exo reaction are more similar in energy, however the endo reaction has the lowest activation energy and is therefore the kinetically preferred product, and will be formed fastest, needing the least energy for the reaction to occur. This is due to the secondary orbital interactions between the p orbitals of the oxygen being able to overlap with those in xylylene in the endo orientation, however as the oxygen points away from xylyene in the exo orientation, this stabilisation is not possible. The reaction energies show that all of these reactions are thermodynamically favourable, however the cheletropic reaction has the greatest reaction energy and so is the thermodynamically preferred product.This is due to there being a loss of three π bonds in the Diels-Alder reactions with one π bond and two σ bonds formed, compared to the loss of only two π bonds in the cheletropic reaction, with again one π bond and two σ bonds formed. The endo and exo products are very similar in energy, and are both higher in energy than the cheletropic product, however the endo product has a slightly higher energy than the exo, therefore has a slightly greater reaction energy.

Alternative Diels-Alder Reactions

Another option for a Diels-Alder reaction comes from the diene within the 6-membered ring of xylylene, and this could be a endo or an exo reaction, as for the previous Diels-Alder reaction. The reaction coordinate for these were also visualised with the IRC at the PM6 level, and can be seen in figure 15. As before the bond formation is asynchronous, however unlike before, due to the fact that bond formation is occuring at the 6-membered ring, there is no opportunity for an aromatic system to form.

Figure 16. Animations of the IRCs for the internal endo and exo Diels-Alder reactions
Internal Endo Diels-Alder	Internal Exo Diels-Alder

Table 4. Energies of the reactants, transition states and products for the internal Diels-Alder reactions
	Energy (kJmol^-1)
Reaction type	SO₂	Xylylene	Reactant total	Transition State	Activation Energy	Product	Reaction Energy
Exo	-311.38	466.43	154.94	275.82	120.88	176.70	21.77
Endo	-311.38	466.43	154.94	267.98	113.05	172.26	17.32

From the reaction energies shown in table 4 it can be seen that these reactions are endothermic and therefore not thermodynamically favourable, which is due to the lack of aromaticity to stabilise the products. The activation energy for both reactions is also very high compared to the previous Diels-Alder reactions, showing that the reactions are also kinetically unfavourable. The endo reaction is kinetically and preferred over the exo reaction, which is due to the stabilisation that comes from the orbital interaction of the p orbital of the oxygen with that of the diene, as before.

Electrocyclic reaction

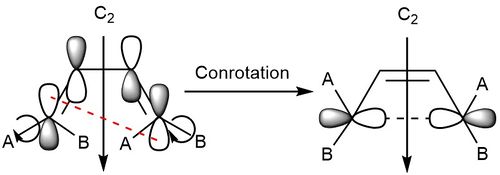
The electrocyclic reaction of a diene was investigated at the PM6 level. Figure 16 shows the reaction scheme for this reaction. This is a thermal reaction rather than a photochemical reaction as at the PM6 level, the molecules are in the ground state, and for a photochemical reaction to occur, they would need to be able to reach an excited state. This means that as there are 4n electrons, therefore the groups on the diene will both rotate in the same direction (conrotation). This results in both hydrogens facing upwards as can be seen in the reaction path vibration (figure 17)

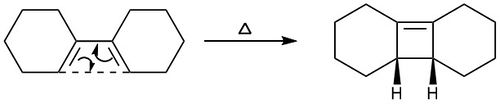
Figure 17. Vibration of reaction path

(Very close but you're using Ψ4 Tam10 (talk) 13:36, 4 April 2018 (BST))

Figure 18 shows the formation of the HOMO of the product, with the C₂ axis of symmetry labelled. This axis of symmetry is used to label the orbitals as either symmetric or asymmetric. Figure 19 shows the correlation diagram for the reaction, where it can be seen that the order of the occupied orbitals is reversed, with symmetric HOMO of the reactant forming the symmetric σ orbital formed in the product, while the HOMO orbital of the product (the π orbital) has the same symmetry as the HOMO-1 of the reactant. The same occurs with the unoccupied orbitals, with the asymmetric LUMO of the reactant forming the asymmetric LUMO+1 of the product (the σ^* orbital), and the LUMO+1 orbitals of the reactant forming the LUMO of the product (the π^* orbital)

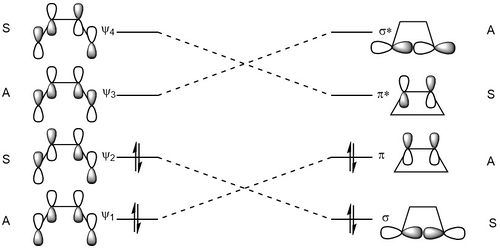
The reaction goes through a mobius transition state, with a node in the phases of the orbitals. As it is a 4n electron reaction, the transition state is termed 'aromatic'.^[7] This can be seen in the visualisation of the transition state orbitals in figure 16.

Figure 20. Reactant, product and transition state MOs

Reactant MOs

HOMO - 1

HOMO

LUMO

LUMO + 1

Product MOs

HOMO - 1

HOMO

LUMO

LUMO + 1

Transition State MOs

HOMO - 2

HOMO

LUMO

LUMO + 1

Conclusion

For all of the reactions, the transition state was found and optimised successfully. It was found that the first Diels-Alder reaction was normal demand, while the second Diels-Alder was inverse electron demand, due to the electron rich nature of the dienophile. For both exercises 2 and 3, it was found that the endo Diels-Alder reaction was thermodynamically preferred to the exo reaction, due to the stabilising secondary orbital overlap. For exercise 3, the cheletropic product was the thermodynamically preferred product, while the alternate Diels-Alder reactions were thermodynamically unfavourable as there is no aromatic ring formation as for the original Diels-Alder reactions and the cheletropic reaction. In the electrocyclic reaction it was found to proceed in a conrotatory fashion, as expected for a thermal 4n eletron elecrocyclic reaction. This could be extended by investigated the photochemical reaction, which would preocceed in a disrotatory fashion, however the PM6 level could not be used for these calculations due to the need for excited states.

Files

References

↑ Lewars E, Computational Chemistryː The Concept of the Potential Energy Surface,2016,Springer International Publishing,Cham, pp 9-49
↑ Yepes, D et al.Phys. Chem. Chem. Phys., 2012,14, 11125-11134
↑ Stewart, J J Mol Model, 2007, 13(12), 1173-1213
↑ Devlin, F. J. et al.J. Phys. Chem., 1995, 99 (46), 16883–16902
↑ Mantina, M et al.J. Phys. Chem. A,2009, 113, 19, 5806-5812
↑ Mikhailov, B. M.,Bull. Acad. Sci. USSR, Div. Chem. Sci.,1960, 9,8,1284–1290
↑ Dolbier, W. RAcc. Chem. Res., 1996, 29, 471-477

[1] Lewars E, Computational Chemistryː The Concept of the Potential Energy Surface,2016,Springer International Publishing,Cham, pp 9-49

[2] Yepes, D et al.Phys. Chem. Chem. Phys., 2012,14, 11125-11134

[3] Stewart, J J Mol Model, 2007, 13(12), 1173-1213

[4] Devlin, F. J. et al.J. Phys. Chem., 1995, 99 (46), 16883–16902

[5] Mantina, M et al.J. Phys. Chem. A,2009, 113, 19, 5806-5812

[6] Mikhailov, B. M.,Bull. Acad. Sci. USSR, Div. Chem. Sci.,1960, 9,8,1284–1290

[7] Dolbier, W. RAcc. Chem. Res., 1996, 29, 471-477

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Introduction

Exercise 1

MO diagram

Bond Distances

Reaction path Vibration

Exercise 2

MO Diagrams

Secondary Orbital Interactions

Energies

Exercise 3

Visualisation of the reaction coordinate

Energies

Alternative Diels-Alder Reactions

Electrocyclic reaction

Conclusion

Files

Exercise 1

Exercise 2

Exercise 3

Electrocyclic Reaction

References